Конструкция авиа двигателя. Конструкция и прочность АД Тараканов Д.Е 0919.0007. Курсовой проект по дисциплине конструкция и прочность авиационных двигателей тема Анализ статической и динамической прочности рабочей лопатки первой ступени турбины гтд тв2117
 Скачать 2.01 Mb. Скачать 2.01 Mb.
|
ВведениеВ XXI веке стран, умеющих проектировать и производить современные авиационные двигатели, меньше, чем государств, обладающих собственной ядерной программой. В этом нет ничего удивительного: по сложности конструкции и производства современные авиадвигатели сопоставимы с космической техникой. Современное состояние и тенденции развития авиационного двигателестроения предъявляют повышенные требования к знаниям и навыкам инженеров, эксплуатирующих авиационную технику. Выполнение курсового проекта позволяет понять методологию и основы проектирования современных авиационных двигателей. Целями курсовой работы является: 1 Выполнить расчеты и сделать заключение о выполнении или невыполнении условия прочности рабочей лопатки первой ступени турбины, под действием статических нагрузок на взлетном режиме работы двигателя в условиях, соответствующих исходным данным. В случае выполнения условия прочности необходимо определить наиболее слабое с точки зрения прочности сечение лопатки. 2 Проверить наличие опасных резонансных режимов работы исследуемой лопатки в рабочем диапазоне частот вращения ротора и в резервных зонах вблизи частот малого газа и взлетного режима. Необходимо вычислить частоты собственных колебаний рабочей лопатки по первым трем изгибным формам. Считается что при наличии резонансов по первым трем изгибным формам, выход действующих напряжений за предел усталостной прочности материала является наиболее вероятным. 1 Теоретическая основа работыВывод формулы для растягивающих напряжений от центробежных сил, действующих на массу пера лопатки Условие равновесия отсеченной части пера: P 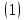 ц(r) = ц(r) = 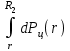 = σц(r)·F(r) , = σц(r)·F(r) , где Pц(r) – центробежная сила, действующая на отсеченную часть пера лопатки; dPц(r) – элементарная центробежная сила, действующая на элемент пера лопатки, ограниченный сечениями на радиусах r и (r+dr); σц(r) – напряжение растяжения, вызванное приложением центробежной силы Pц(r) (принимается постоянным по рассматриваемому сечению); F(r) – площадь сечения лопатки на радиусе r. Элементарная центробежная сила может быть записана в виде: d 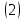 Pц(r) = dm(r) ·r ·ω2, Pц(r) = dm(r) ·r ·ω2, где dm(r) – масса элемента пера лопатки, которая равна: d 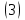 m(r) = ρ·F(r)·dr, m(r) = ρ·F(r)·dr,здесь ρ – плотность материала лопатки. Подставляя dm(r) в выражение для dPц(r), а полученное выражение в формулу для Pц(r), получим: σ 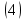 ц(r)·F(r)= ц(r)·F(r)=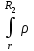 ·F(r)·r· ω2·dr, ·F(r)·r· ω2·dr,Нас интересует распределение напряжений растяжения по длине лопатки (т.е. по радиусу r в пределах от R1 до R2), поэтому перепишем (4) ввиде: σ 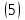 ц(r)= ц(r)=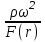 · ·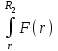 ·r·dr ·r·drЕсли F(r)=const, то 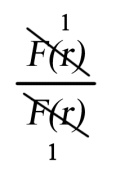 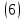 σц(r) = ρω2 σц(r) = ρω2 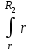 dr = ρω2 dr = ρω2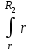 dr drИзвестно, что: 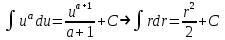 и  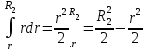 Тогда: 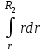 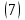 σц(r) = ρω2 = ρω2· σц(r) = ρω2 = ρω2·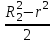 Из полученной формулы (7) следует, что чем меньше r, тем больше напряжение σц(r). При этом максимальное значение напряжения растяжения принимает при минимально возможном значении радиуса пера лопатки rmin = R1: 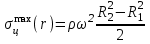 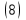  Однако зависимость площади сечения реальной лопатки от радиуса r не соответствует закону F(r) = const (значения F1 и F2 отличаются в 2…4 раза). По мнению некоторых специалистов: Макарова Н.В., Шерлыгина Н.А., Соловьева Б.А., Куландина А.А. и др. реальное изменение площади поперечного сечения лопатки по радиусу r может быть с достаточной точностью описано экспоненциальной зависимостью вида [1, с. 40], [2, с. 101]: F 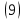 (r) =F1·e (r) =F1·e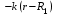 , ,где: F1 – площадь корневого сечения лопатки; R1 – радиус корневого сечения лопатки; e – основание натурального логарифма. Выбор указанными выше специалистами зависимости (9) в качестве аппроксимирующей реальную может быть объяснен тем, что в результате такого выбора интеграл (5) сравнительно легко «берется» «в квадратурах». На такой вариант расчетов их натолкнуло предложение доцента кафедры механики ВАУ-ОЛАГА Чернова Константина Ивановича. Есть все основания назвать получающуюся в итоге формулу для расчета растягивающих напряжений в сплошной вращающейся лопатке «формулой Чернова». На такой вывод наталкивает то обстоятельство, что этой аппроксимацией не пользуются авторы учебника КИИГА «Конструкция и прочность авиационных газотурбинных двигателей» Лозицкий Л.П. и автор конспекта лекций «Прочность и динамика узлов авиационных газотурбинных двигателей», заведующий кафедрой двигателей МГТУ ГА Умушкин Б.П. [3, с. 223-227], [4]. Коэффициент k в показателе экспоненциальной зависимости (9) при известных значениях F1 и F2 может быть найден следующим образом, в соответствии с (9): F(R2)=F2=F1·e 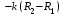 = =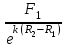 ⇒ ⇒⇒ e 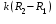 = =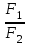 Логарифмируя левую и правую части, получим: 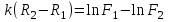 ⇒ ⇒⇒ 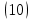 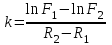 , ,F1>F2>0; R2>R1>0 ⇒k>0 Для типичных геометрических параметров лопатки турбины первой ступени двигателя ТВ2-117 (Методическое указание к выполнению курсового проекта, 1990): R1=0,400 м; R2=0,525 м; F1=0,00038 м2; F2=0,000124 м2. 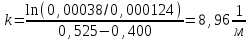 С использованием экспоненциальной аппроксимации (9) зависимости для F(r) распределения напряжений растяжения от центробежной силы примет вид: 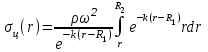 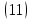 Выделяя постоянные величины в подынтегральном выражении, получим: 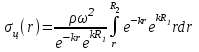 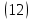 Вынося постоянный множитель 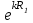 из под знака интеграла, будем иметь: из под знака интеграла, будем иметь: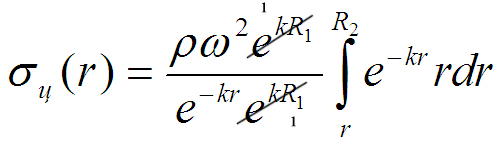 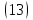 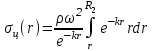  Теперь необходимо этот интеграл взять “по частям”. Формула интегрирования “по частям” имеет вид: 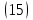 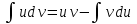 Для того чтобы использовать эту формулу, подынтегральное выражение должно иметь вид 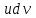 . Перепишем интеграл в формуле (14) в следующем виде: . Перепишем интеграл в формуле (14) в следующем виде: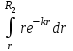 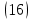 Пусть сомножитель r=u, тогда оставшиеся сомножители e-kr·dr должны образовать дифференциал 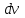 , однако из произведения e-kr·dr дифференциала не получается, поэтому необходимо продифференцировать e-kr по r, и тогда получится: , однако из произведения e-kr·dr дифференциала не получается, поэтому необходимо продифференцировать e-kr по r, и тогда получится: 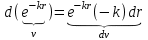 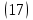 Проявим хитрость: умножим и разделим подынтегральное выражение на –k (имеем право, т.к. –k – постоянная величина) и 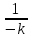 вынесем за знак интеграла: вынесем за знак интеграла: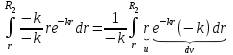  Теперь под знаком интеграла оказалось выражение, к которому можно применить формулу интегрирования по частям: 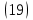   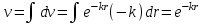 Табличный интеграл: 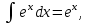 и если принять -k·r=x,тогда (-k)·dr=dx и если принять -k·r=x,тогда (-k)·dr=dxРасставляя пределы интегрирования для первого слагаемого в правой части выражения (19) получим: 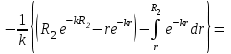 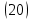 , ,Для того чтобы вычислить определенный интеграл в формуле (20) снова используем тот же прием: умножим и разделим подынтегральное выражение на (-k) и вынесем 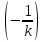 за знак интеграла. В результате получим: за знак интеграла. В результате получим: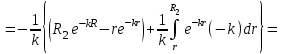    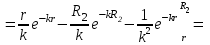 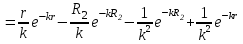  Подставляя полученное выражение (23) в формулу для напряжений 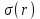 (14), получим: (14), получим: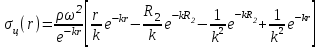 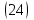 Умножим и разделим правую часть на k2: 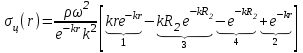 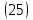 Разделим выражение в квадратных скобках на e-kr и вынесем делитель за скобки: 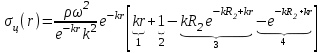  Окончательно получаем: 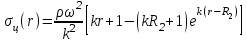  |
