Моделирование транспортных процессов. Курсовой проект по дисциплине Моделирование транспортных процессов

• Название: Курсовой проект по дисциплине Моделирование транспортных процессов
• Анкор: Моделирование транспортных процессов
• Дата: 27.05.2020
• Размер: 1.42 Mb.
• Имя файла: Prosov_modTP.docx
• Тип: Курсовой проект; #125849
• страница: 3 из 3

3. Постановка транспортной задачи, математическая модель

Однородный продукт, сосредоточенный у m поставщиков Ai в количестве ai (i = 1, 2,…,m) единиц соответственно, необходимо доставить n потребителям Bj в количестве bj (j = 1, 2,…,n) единиц. Известна стоимость cij перевозки единицы груза от i-го поставщика j-му потребителю. Необходимо составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности и имеющий минимальную стоимость.

Обозначив через xij количество единиц груза, запланированного к перевозке от i-го поставщика к j-му потребителю, записывается математическая модель задачи: найти наименьшее значение целевой функции

m n

min Σ Σ cij xij,

i=1 j=1

при ограничениях:

n

Σ xij = ai, (i = 1, 2,…,m);

j=1

m

Σ xij = bj, (j = 1, 2,…,n);

i=1

xij ≥ 0;

m n

Σ ai = Σ bj.

i=1 j=1

3. Построение матрицы оптимальных грузопотоков

Исходную информацию сводят в табл. Существует несколько схем построения первоначального решения: метод северо-западного угла, минимальной стоимости, двойного предпочтения, Фогеля и др.

Метод северо-западного угла. Не учитывая стоимости перевозки, удовлетворяется потребность первого потребителя B1 за счет запаса поставщика A1. Сравниваются величины a1 и b1.

Меньший из объемов записывается в клетку A1 B1. Если a1 < b1, то запасы поставщика A1 израсходованы, строка A1 вычеркивается и следующей заполняется клетка A2 B1. Если a1 > b1, то зачеркивается столбец B1 и следующей заполняется клетка A1 B2. Процедура повторяется до загрузки клетки Am Bn. При использовании данного метода стоимость перевозки не учитывается, поэтому план далек от оптимального.

Метод минимальной стоимости. Выбирается клетка с наименьшей стоимостной оценкой cij и производится ее загрузка наименьшим из объемов ai и bj. Из рассмотрения исключается строка Ai, если aibj. В случае ai=bj вычеркивается строка Ai и столбец Bj.

Из оставшейся части матрицы вновь выбирается клетка с наименьшей стоимостной оценкой и процедура повторяется до распределения всех объемов производства и потребления.
Таблица 5 – Матрица грузопотоков без выплонения расчётных мероприятий

Поставщики	1	2	6	10	12	13	16	18	Объемы производства
8	5028	28	9	4012	14	106	23	25	100
20	1015	2015	307	13	2010	7	3010	12	110
19	5	9	24	28	19	24	12	1005	100
Объемы потребления	60	20	30	40	20	10	30	100	310

Т р= 50*28+40*12+10*6+10*15+20*15+30*7+20*10+30*10+100*5= 3600ткм

1400 480 60 150 300 210 200 300 500

Матрица оптимальных грузопотоков

Таблица 6 – Матрица оптимальных грузопотоков

Поставщики	Потенциалы	1	2	6	10	12	13	16	18	Объемы производства
8	α β	16	19	9	12	14	6	14	16
	0	28	28	309	4012	204	106	23	25	100
20	-4	15	2015	7	13	10	7	3010	6012	110
19	-11	605	9	24	28	19	24	12	405	100
Объемы потребления		60	20	30	40	20	10	30	100	310

Т р= 30*9+40*12+20*4+10*6+20*15+30*10+60*12+60*5+40*5=2710 ткм

270 480 80 60 300 300 720 300 200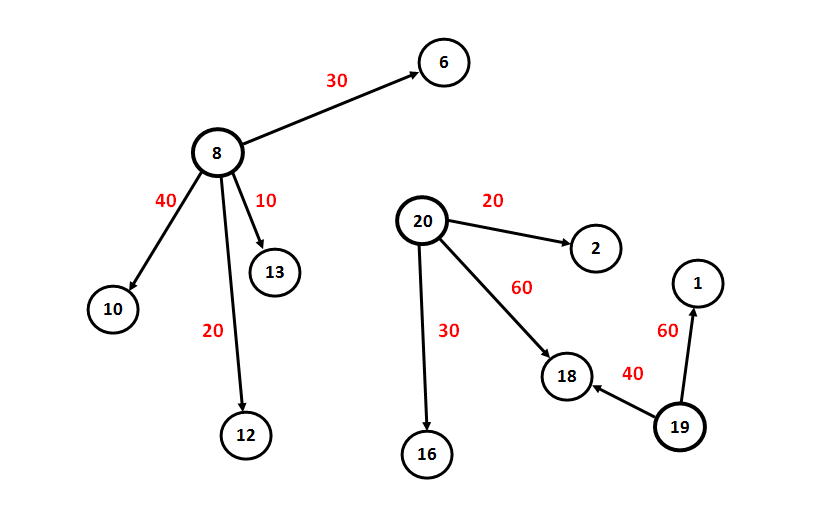



Рисунок 4 – Схема поставок от ГОП к ГПП

Заключение

В заключение отметим, что выбрана оптимальная схема движения грузопотоков от грузоотправителей к грузополучателям. Это позволит с наименьшими затратами обеспечить транспортную работу, что безусловно выгодно для каждого предприятия.

По сравнению с произвольным распределением между грузоотправителями и грузополучателями нахождение матрица оптимальных грузопотоков позволяет сократить транспортную работу на 75,3% по сравнению с изначальной величиной.

Список литературы

Список основной литературы

1. 
   Геронимус, Б.Л. Экономико-математические методы в планировании на автомобильном транспорт: учебник для автотрансп. техникумов / Б. Л. Геронимус, Л.В Цапфин. – М.: Транспорт, 1988, – 192 с.
   
2. 
   Кожин, А.П. Математические методы в планировании и управлении грузовыми автомобильными перевозками: учеб. пособие для вузов / А.П. Кожин, В.Н. Мезенцев. – М.: Транспорт, 1994, - 304 с.
   
3. 
   Просов, С.Н. Модель кольцевой маршрутизации перевозок грузов помашинными отправками: лабораторный практикум и методические указания для практических занятий по курсу “Моделирование транспортных систем” / С.Н. Просов. – М.: МАДИ, 2016, – 48 с.
   
4. 
   Просов, С.Н. Проектирование автотранспортных систем доставки: учебное пособие / С.Н. Просов. – М.: МАДИ, 2017, – 100 с.
   

Дополнительная литература

5. 
   Программа обработки электронных таблиц MS Excel.
   
6. 
   Просветов, Г.И. Математические методы в логистике: Учебно-методическое пособие / Г.И. Просветов.–М.: Изд-во РДЛ, 2006, –272 с.
   
7. 
   Таха, Х. Введение в исследование операций / Х. Таха. – 7-е изд., пер. с англ. – М.: Издательский дом «Вильямс», 2005, – 912 с.