Автоматизация ректификационной колонны К-2 САПНО. Курсовой проект по дисциплине Системы автоматики предприятий нефтегазовой отрасли по теме Автоматизация ректификационной колонны к2

• Название: Курсовой проект по дисциплине Системы автоматики предприятий нефтегазовой отрасли по теме Автоматизация ректификационной колонны к2
• Анкор: Автоматизация ректификационной колонны К-2 САПНО
• Дата: 13.03.2023
• Размер: 2.35 Mb.
• Имя файла: Kursovoi_Vyazovsk..docx
• Тип: Курсовой проект; #986584
• страница: 5 из 8

OutputName: {'Температура'}

OutputUnit: {'гр.С'}

InputData: [100x1 double]

u: 'Same as InputData'

InputName: {'Мощность '}

InputUnit: { '%' }

Period: Inf

InterSample: 'zoh'

Ts: 3

Tstart: []

SamplingInstants: [100x0 double]

TimeUnit: ''

ExperimentName: 'Exp1'

Notes: {}

UserData: []

Для графического представления данных (рис.6) воспользуемся командой

>>plot(dan)

Рис.3. Исходные данные для идентификации ТОУ.

Проведем параметрическое оценивание моделей с помощью GUI, для этого вводим команду

>> ident

В результате ее выполнения появляется диалоговое окно (рис. 4):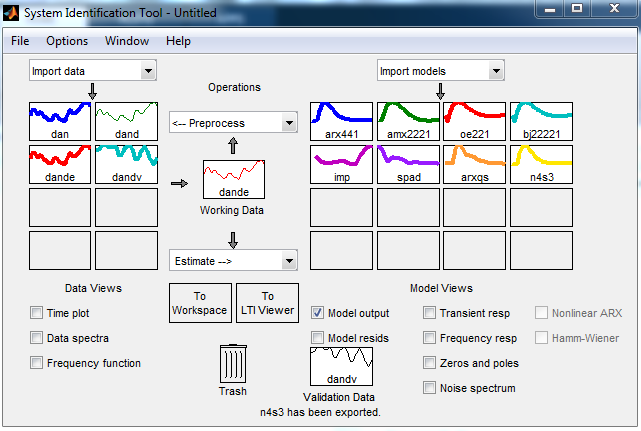

Рис.4 Диалоговое окно графического интерфейса

System Identification Toolbox.

Для дальнейшего использования полученных исходных данных необходимо провести предварительную обработку этих данных с целью удаления тренда из набора данных и если необходимо отфильтровать данные с помощью имеющихся средств в пакете System Identification Toolbox.

Данные операции проведем в графическом интерфейсе System Identification Toolbox, который запускается из командной строки командой:

>> ident

Opening System Identification Tool ....... done.

Импортируем файл данных в среду интерфейса с помощью команды data – import

Запустим режим быстрого старта, для чего в падающем меню Operations выберем Quick Start. При выборе этого режима производится:

-удаление тренда из массива экспериментальных данных;

- формирование усеченных массивов данных с именами dande и dandv для построения моделей

Рис. 5. – Температура и давлении фракции внутри колонны

,

Рис. 6. Показатели адекватности моделей

Для анализа модели ТОУ возьмем модель n4s3 , для чего перетащим ее на иконку To Workspace, при этом модель n4s3 появится в рабочем пространстве MATLAB.

Полученная модель представлена в так называемом тета – формате и является дискретной. Для преобразования модели из тета - формата в вид удобный для дальнейшего использования в пакете System Identification Toolbox имеются специальные функции.

Преобразуем модель тета - формата многомерного объекта в вектор передаточных функций, связанных с выбранным входом:

>> [num,den]=th2tf(n4s3)

num =0 -0.0036 0.0052 0.0729

den = 1.0000 -1.6976 0.9643 -0.1779

>> Wz=tf(num,den,Ts)

Wz =-0.05999 z^2 + 0.04869 z + 0.01253

---------------------------------

z^5 - 1.251 z^4 + 0.3763 z^3к

Sample time: 3 seconds

Discrete-time transfer function.

>> Ws=d2c(wz)

Ws = 0.02761 s^2 - 0.02182 s + 0.006256

Transfer function:

0.3928 s^2 - 0.1036 s + 0.2589

---------------------------------

s^3 + 12.4 s^2 + 3.955 s + 0.2669

.>> step(Ws)

Рис. 7. График переходных процессов модели

Определим частотные характеристики модели (рис. 8) с помощью команды:

>> bode(Ws)

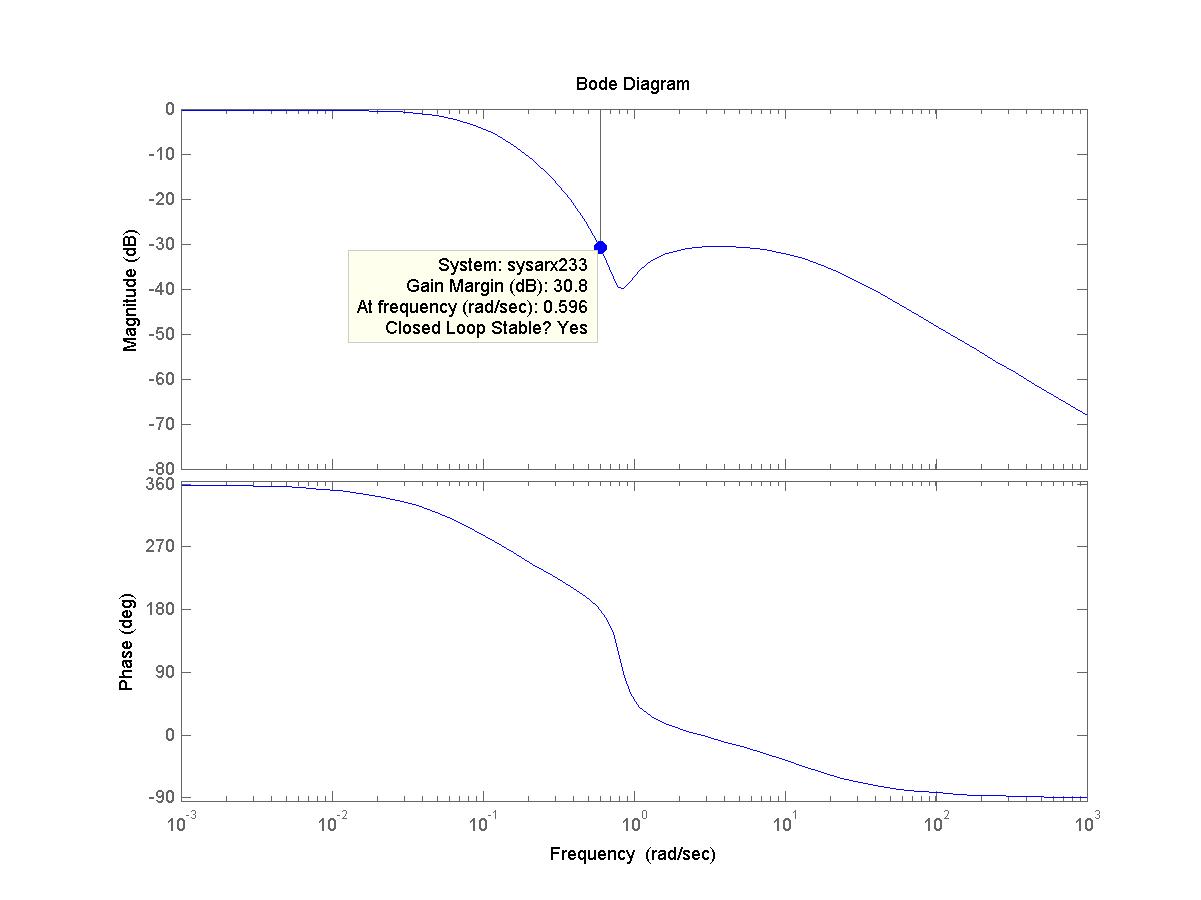
Рис. 8. Частотные характеристики модели

Запас устойчивости по амплитуде:

* Для непрерывной: 9.68 dB.

Значения запасов устойчивости можно определить также и в режиме командной строки MATLAB с помощью команд:

>> [Gm,Pm,Wcg,Wcp]=margin(Ws)

Gm = 34.7465

Pm = Inf

Wcg = 0.5964

Wcp = NaN