пояснительная записка. Пример оформления пояснительной записки. Курсовой проект по дисциплине Теория принятия решений
 Скачать 221.62 Kb. Скачать 221.62 Kb.
|
 Министерство сельского хозяйства Российской Федерации ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ» Институт управления рисками и комплексной безопасности Кафедра цифровых систем обработки информации и управления КУРСОВОЙ ПРОЕКТ по дисциплине «Теория принятия решений» Решение задач динамического программирования Пояснительная записка ОГАУ 09.03.01.3020.105 ПЗ Руководитель проекта доцент ___________ В.Б. Дудоров «___» ____________ 2020 г. Исполнитель студент группы 31 ИВТ Д.А. Беляев «» 2020 г. Оренбург 2020 Аннотация В курсовом проекте изучена теория касательно динамического программирования и использования этого метода при принятии управленческих решений. Данный проект содержит 3 раздела. Первый раздел посвящен общей теории динамического программирования. Здесь рассмотрены такие вопросы как, задача, постановка задачи и общая структура динамического программирования. Во втором разделе дается описание типовых задач динамического программирования. Были выбраны 2 задачи: задача оптимального распределения инвестиций предприятия и задача оптимальной загрузки рюкзака предметами. Также были разобраны их модели и алгоритмы решения. В третьем разделе рассмотрена разработка приложения и его тестирование. А именно вопросы выбора языка программирования, разработки графического интерфейса, оптимизации и эффективности приложения. Курсовой проект содержит 22 страницы без приложений, 2 таблицы, 4 рисунка, 17 источников и 2 приложения Содержание Введение 5 1 Динамическое программирование 6 1.1 Задача динамического программирования 6 1.2 Постановка задачи динамического программирования 7 1.3 Общая структура динамического программирования 8 2 Типовые задачи динамического программирования 10 2.1 Задача оптимального распределения инвестиций предприятия 10 2.2 Задача оптимальной загрузки рюкзака предметами 13 3 Разработка приложения и его тестирование 15 3.1 Выбор языка программирования 15 3.2 Разработка задачи распределения ресурсов 15 3.3 Разработка задачи о рюкзаке 17 Заключение 21 Список использованных источников 22 Приложение А 23 Приложение Б 24 Введение В настоящее время многие организации в своей деятельности сталкиваются с математическими моделями. Моделирование и построение математической модели экономического объекта позволяют свести экономический анализ производственных процессов к математическому анализу и принятию эффективных решений. В самых разнообразных областях теоретической и практической деятельности часто оказывается целесообразным принимать решения не сразу, а постепенно, шаг за шагом. Принятие решение, таким образом, рассматривается как процесс, состоящий из нескольких этапов. Это позволяет спланировать программу будущих действий. Поскольку вариантов возможных планов – программ множество, то, необходимо из них выбрать лучший, оптимальный по какому-либо критерию в соответствии с поставленной целью. Динамическое программирование является одним из наиболее эффективных методов решения подобных задач, чем и объясняется актуальность данного проекта. Объект исследования: задачи оптимизации при принятии решений. Предметом исследования является метод динамического программирования. Целью курсового проекта является исследование метода динамического программирования и его применение для решения задач. Для достижения поставленной цели решаются следующие задачи: 1) Изучить теорию динамического программирования, постановку его общей задачи, а также алгоритм решения. 2) Решить классические задачи динамического программирования, при этом построив их математическую модель Разработать приложение, позволяющее искать оптимальный план типовых задач динамического программирования. Провести его тестирование, используя исходные данные решенных задач 1 Динамическое программирование 1.1 Задача динамического программирования Большинство методов исследования операций связано в первую очередь с задачами вполне определенного содержания. Классический аппарат математики оказался малопригодным для решения многих задач оптимизации, включающих большое число переменных и/или ограничений в виде неравенств. Несомненна привлекательность идеи разбиения задачи большой размерности на подзадачи меньшей размерности, включающие всего по нескольких переменных, и последующего решения общей задачи по частям. Именно на этой идее основан метод динамического программирования. Динамическое программирование (ДП) — это метод решения задач с оптимальной подструктурой и перекрывающимися подзадачами, который намного эффективнее, чем решение перебором. Модели динамического программирования могут применяться, например, при разработке правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа; при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; при распределении дефицитных капиталовложений между возможными новыми направлениями их использования; при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены; при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т.д. Словосочетание динамическое программирование впервые было использовано в 1940-х годах Р. Беллманом для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения задачи, «предшествующей» ей. В 1953 г. он уточнил это определение до современного. Вклад Беллмана в динамическое программирование был увековечен в названии уравнения Беллмана, центрального результата теории динамического программирования, который переформулирует оптимизационную задачу в рекурсивной форме. Слово «программирование» в словосочетании «динамическое программирование» в действительности к традиционному программированию (написанию кода) почти никакого отношения не имеет и происходит от словосочетания «математическое программирование», которое является синонимом слова «оптимизация». Поэтому слово «программа» в данном контексте скорее означает оптимальную последовательность действий для получения решения задачи. Метод динамического программирования можно использовать для решения весьма широкого круга задач, включая задачи распределения ресурсов, замены и управления запасами, задачи о загрузке. Характерным для динамического программирования является подход к решению задачи по этапам, с каждым из которых ассоциирована одна управляемая переменная. Набор рекуррентных вычислительных процедур, связывающих различные этапы, обеспечивает получение допустимого оптимального решения задачи в целом при достижении последнего этапа. Однако методы ДП успешно применяются также для решения задач, в которых фактор времени не учитывается. По этой причине более удачным представляется термин многоэтапное программирование, отражающий пошаговый характер процесса решения задачи. Фундаментальным принципом, положенным в основу теории ДП, является принцип оптимальности. По существу, он определяет порядок поэтапного решения допускающей декомпозицию задачи с помощью рекуррентных вычислительных процедур. 1.2 Постановка задачи динамического программирования Динамическое программирование позволяет осуществлять оптимальное планирование управляемых процессов. Под «управляемыми» понимаются процессы, на ход которых мы можем в той или другой степени влиять. Пусть предполагается к осуществлению некоторое мероприятие или серию мероприятий, преследующую определенную цель. Спрашивается: как нужно организовать операцию для того, чтобы она была наиболее эффективной? Для того, чтобы поставленная задача приобрела количественный, математический характер, необходимо ввести в рассмотрение некоторый численный критерий W, которым мы будем характеризовать качество, успешность, эффективность операции. Критерий эффективности в каждом конкретном случаи выбирается исходя из целевой направленности операции и задачи исследования (какой элемент управления оптимизируется и для чего). Сформулируем общий принцип, лежащий в основе решения всех задач динамического программирования («принцип оптимальности»): «Каково бы ни было состояние системы S перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным». Динамическое программирование – это поэтапное планирование многошагового процесса, при котором на каждом этапе оптимизируется только один шаг. Управление на каждом шаге должно выбираться с учетом всех его последствий в будущем. При постановке задач динамического программирования следует руководствоваться следующими принципами: Выбрать параметры (фазовые координаты), характеризующие состояние S управляемой системы перед каждым шагом. Расчленить операцию на этапы (шаги). Выяснить набор шаговых управлений xk для каждого шага и налагаемые на них ограничения. Определить какой выигрыш приносит на k-ом шаге управление xk, если перед этим система была в состоянии S, т.е. записать «функцию выигрыша»: 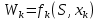 Определить, как изменяется состояние S системы S под влиянием управление xk на k-ом шаге: оно переходит в новое состояние 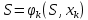 Записать основное рекуррентное уравнение динамического программирования, выражающее условный оптимальный выигрыш Wk(S) (начиная с k-го шага и до конца) через уже известную функцию Wk+1(S): 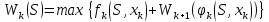 Этому выигрышу соответствует условное оптимальное управление на k-м шаге xi(S) (причем в уже известную функцию Wk+1(S) надо вместо S подставить измененное состояние: 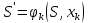 Произвести условную оптимизацию последнего (m-го) шага, задаваясь гаммой состояний S, из которых можно за один шаг дойти до конечного состояния, вычисляя для каждого из них условный оптимальный выигрыш по формуле: 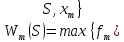 Произвести условную оптимизацию (m-1)-го, (m-2)-го и т.д. шагов по формуле (1.2), полагая в ней k=(m-1),(m-2),…, и для каждого из шагов указать условное оптимальное управление xk(S), при котором максимум достигается. Заметим, что если состояние системы в начальный момент известно, то на первом шаге варьировать состояние системы не нужно - прямо находим оптимальный выигрыш для данного начального состояния S0. Это и есть оптимальный выигрыш за всю операцию 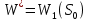 Произвести безусловную оптимизацию управления, «читая» соответствующие рекомендации на каждом шаге. Взять найденное оптимальное управление на первом шаге 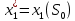 ; для вновь найденного состояния найти оптимальное управление на втором шаге х2* и т.д. до конца. ; для вновь найденного состояния найти оптимальное управление на втором шаге х2* и т.д. до конца.1.3 Общая структура динамического программирования Отыскание оптимальной стратегии принятия набора последовательных решений, в большинстве случаях, производится следующим образом: сначала осуществляется выбор последнего во времени решения, затем при движении в направлении, обратном течению времени, выбираются все остальные решения вплоть до исходного. Для реализации такого метода необходимо выяснить все ситуации, в которых может происходить выбор последнего решения. Обычно условия, в которых принимается решение, называют «состоянием» системы. Состояние системы – это описание системы, позволяющее, учитывая будущие решения, предсказать ее поведение. Нет необходимости выяснять, как возникло то ил иное состояние или каковы были предшествующие решения. Это позволяет последовательно выбирать всего по одному решению в каждый момент времени. Независимо от того, отыскивают оптимальные решения с помощью табличного метода и последующего поиска или аналитическим путем, обычно быстрее и выгоднее производить выбор по одному решению в один момент времени, переходя затем к следующему моменту и т.д. К сожалению, таким методом можно исследовать не все процессы принятия решений. Необходимым условием применения метода динамического программирования является аддитивность цен всех решений, а также независимость будущих результатов от предыстории того или иного состояния. Если число решений очень велико, то можно построить относительные оценки состояний так, чтобы оценки, отвечающие каждой паре последовательных решений, отличались друг от друга на постоянную величину, представляющую собой средний «доход» на решение. Также можно выполнять дисконтирование доходов от будущих решений. Необходимость в этом иногда появляется в том случае, когда решение принимаются редко, скажем раз в году. Тогда уже не нужно рассматривать последовательно 1,2,3…решения, чтобы достичь решения с большим номером. Вместо этого можно непосредственно оперировать функциональным уравнением, что, как правило, дает существенную выгоду с точки зрения сокращения объема вычислений. Изучив метод динамического программирования для решения задач выделены его следующие преимущества: 1) сравнительная простота и однотипность расчетов, что является удобным для алгоритмизации и программирования задач при их решении на ЭВМ; 2) снижение трудоемкости решения задач за счет более полного использования свойств управляемых систем; 3) отсутствие специальных ограничений на природу, характер и свойства функций и т.п. Недостатком же является использование большого количества оперативной памяти для хранения таблиц промежуточных решений. 2 Типовые задачи динамического программирования 2.1 Задача оптимального распределения инвестиций предприятия В производственной практике очень часто возникают задачи на оптимальное распределение ресурсов между предприятиями или внутри предприятия. Кроме того, к задаче оптимального распределения ресурсов можно отнести еще ряд задач. Например, задачу о размещении по торговым и складским помещениям какого-либо товара, задачу о распределении средств между различными отраслями промышленности и т.п. Классическая постановка задачи выглядит следующим образом: планируется распределение начальной суммы средств X, между n предприятиями П1, П2, П3, … Пn, причем средства выделяются только в размерах, кратных определенному и заданному числу. Предполагается, что выделенные предприятию Пk в начале планового периода средства x приносят доход равный 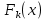 . .Будем считать, что: 1) доход, полученный от вложения средств в предприятие, не зависит от вложения средств в другие предприятия; 2) доход, полученный от разных предприятий, выражается в одинаковых единицах; 3) общий доход равен сумме доходов, полученных от распределения средств по всем предприятиям. Определить, какое количество надо выделить каждому предприятию, чтобы суммарный доход был максимальным. Обозначим через 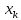 количество средств, выделенных предприятию Пk, тогда математическая модель данных имеет вид: количество средств, выделенных предприятию Пk, тогда математическая модель данных имеет вид: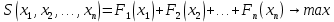 , ,где xk – натуральное, k 1, 2, …, n. Вложим сформулированную задачу в схему динамического программирования. Для этого надо построить управляемую динамическую систему и показать, что целевая функция является аддитивной. Для этого введем искусственно дискретное время. Будем условно считать, что вначале выделяем средства предприятию П1, затем П2 … Пn. Тогда под k-м шагом будем понимать выделение средств предприятию k. Получим n шагов. Под величиной дохода на k-м шаге, очевидно, будем понимать заданные функции дохода 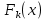 , причем , причем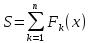 что означает аддитивность целевой функции. что означает аддитивность целевой функции.Начальное и конечное состояния жестко закреплены, а именно: 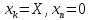 Получили задачу динамического программирования, решить которую означает найти оптимальный набор управлений на каждом шаге, т.е. такой набор управлений 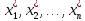 , на котором S max. Теперь к решению задачи можно применить общую схему решения задачи динамического программирования, а именно рекуррентное уравнение Беллмана. , на котором S max. Теперь к решению задачи можно применить общую схему решения задачи динамического программирования, а именно рекуррентное уравнение Беллмана.Приведем пример решения задачи. Известны значения прироста прибыли в каждом из трех отделений сельскохозяйственного предприятия в результате расширения действующих мощностей (таблица 1). Требуется составить план распределения инвестиций в размере 200 у.e., максимизирующий общий прирост прибыли. Таблица 1 – исходные данные задачи о распределении ресурсов
I этап. Условная оптимизация Поскольку предприятий 4, то и количество шагов на первом этапе составит k = 4. В соответствии с алгоритмом динамического программирования рассмотрим случай с k = 4, это означает что все имеющиеся средства выделяются на модернизацию одного предприятия (четвертого). Обозначим через 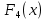 максимально возможный прирост прибыли в этом предприятии, соответствующий выделенной сумме x. максимально возможный прирост прибыли в этом предприятии, соответствующий выделенной сумме x.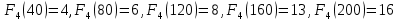 Теперь при k = 3, рассматривается вклад инвестиций в третий и четвертый филиал предприятия, тогда, согласно формуле Беллмана, оптимальное управление на данном шаге выглядит следующим образом: 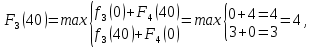 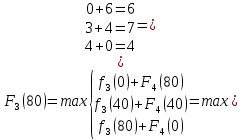 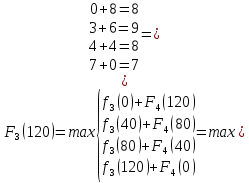 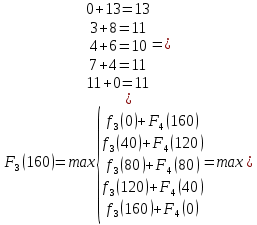 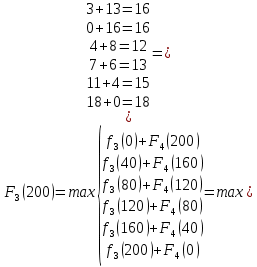 Аналогично высчитываются 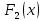 : :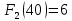 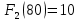 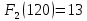 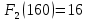 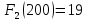 При k = 1, поскольку жестко закреплено конечное состояние, то х принимает только одно значение: 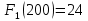 Внесём полученные значения в итоговую таблицу 2. Таблица 2 – конечные вычисления
II этап. Безусловная оптимизация Найдем оптимальные управления на каждом шаге, начиная с первого, пользуясь таблицей 2. Исходя из данных таблицы максимальный доход при инвестиции в 200 у.е. составит 24 у.е., теперь для того, чтобы найти сколько вложены в каждое предприятие для максимальной прибыли высчитывается следующим с начала к концу. То есть в начале мы имеем 200, для того чтобы достичь 24, необходимо вложить в первое 40, затем из 200 вычесть 40, у нас остается 160, при их распределении между тремя предприятиями максимальное решение составит вложение во второе 80 и так до тех пор пока X не станет равным 0. 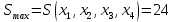 Ответ. Максимальный доход при распределении между данными четырьмя предприятиями 200 млн. руб. составляет 24 млн. руб. и будет получен, если первому предприятию выделить 40 млн. руб., второму выделить 80 млн. руб., а третьему и четвертому – по 40 млн. руб. 2.2 Задача оптимальной загрузки рюкзака предметами В транспортное средство требуется погрузить несколько видов груза, так, чтобы результат загрузки был эффективным. Например, максимизирует стоимость груза, размещенного в транспортном средстве, известна грузоподъемность транспортного средства, вес единицы груза и соответствующая эффективность. Эту задачу еще называют «задачей о рюкзаке». Предполагается, что турист собирается в поход и оптимизирует вес рюкзака, а также ценность вложенного груза. Существуют следующие методы решения задачи: 1) Полный перебор. Как и для других дискретных задач, задачу о рюкзаке можно решить, полностью перебрав все возможные решения. По условию задачи имеется N предметов, которые можно укладывать в рюкзак, и нужно определить максимальную стоимость груза, вес которого не превышает W. Для каждого предмета существует 2 варианта: предмет кладётся в рюкзак, либо предмет не кладётся в рюкзак. Тогда перебор всех возможных вариантов имеет временную сложность O(2N), что позволяет его использовать лишь для небольшого количества предметов. С ростом числа предметов задача становится неразрешимой данным методом за приемлемое время. 2) Метод ветвей и границ. Этот метод является вариацией метода полного перебора с той разницей, что исключаются заведомо неоптимальные ветви дерева полного перебора. Как и метод полного перебора, он позволяет найти оптимальное решение и поэтому относится к точным алгоритмам. Оригинальный алгоритм, предложенный Питером Колесаром в 1967 году, предлагает отсортировать предметы по их удельной стоимости (отношению ценности к весу) и строить дерево полного перебора. Его улучшение заключается в том, что в процессе построения дерева для каждого узла оценивается верхняя граница ценности решения, и продолжается построение дерева только для узла с максимальной оценкой. Когда максимальная верхняя граница оказывается в листе дерева, алгоритм заканчивает свою работу. Способность метода ветвей и границ уменьшать количество вариантов перебора сильно опирается на входные данные. Его целесообразно применять только если удельные ценности предметов значительно отличаются. 3) Методы динамического программирования. Задача о неограниченном рюкзаке. Пусть вес каждого предмета 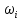 является целым положительным числом. Тогда для решения задачи необходимо вычислить оптимальные решения для всех является целым положительным числом. Тогда для решения задачи необходимо вычислить оптимальные решения для всех 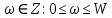 , где W — заданная грузоподъемность. Определим , где W — заданная грузоподъемность. Определим 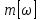 как максимальную ценность предметов, которые можно поместить в рюкзак грузоподъемностью как максимальную ценность предметов, которые можно поместить в рюкзак грузоподъемностью 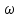 . .Для 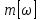 можно записать рекуррентные формулы: можно записать рекуррентные формулы: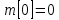 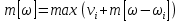 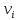 , , 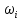 — ценность и вес i-го предмета соответственно, а максимум из пустого множества следует считать равным нулю. — ценность и вес i-го предмета соответственно, а максимум из пустого множества следует считать равным нулю.Фактически последнее уравнение является функциональным уравнением Р. Беллмана или функциональным уравнением динамического программирования. В данном случае для его решения достаточно вычислить все значения 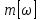 начиная с 0 и до W. Если дополнительно хранить на каждом шаге набор предметов, который реализует максимальную ценность, то алгоритм выдаст и оптимальный набор предметов. начиная с 0 и до W. Если дополнительно хранить на каждом шаге набор предметов, который реализует максимальную ценность, то алгоритм выдаст и оптимальный набор предметов.Так как на каждом шаге необходимо найти максимум из n предметов, алгоритм имеет вычислительную сложность O(nW). Поскольку W может зависеть экспоненциально от размера входных данных, алгоритм является псевдополиномиальным. Поэтому эффективность данного алгоритма определяется значением W. Задача о рюкзаке 0-1. Решение задачи о рюкзаке 0-1 близко к решению предыдущей задачи, но необходимо учесть тот факт, что каждый предмет имеется в единственном экземпляре. Пусть 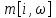 — максимальная ценность предметов, полученных из первых i имеющихся предметов, с суммарным весом не превышающим — максимальная ценность предметов, полученных из первых i имеющихся предметов, с суммарным весом не превышающим 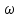 . .Рекуррентные соотношения: 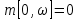 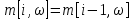 , если , если 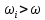 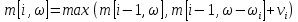 , если , если 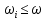 Вычисляя 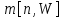 , можно найти точное решение. Если массив , можно найти точное решение. Если массив 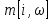 помещается в памяти машины, то данный алгоритм, вероятно, является одним из наиболее эффективных. Этот алгоритм и будет реализован в приложении помещается в памяти машины, то данный алгоритм, вероятно, является одним из наиболее эффективных. Этот алгоритм и будет реализован в приложении3 Разработка приложения и его тестирование 3.1 Выбор языка программирования Для реализации приложения, которое будет удовлетворять всем критериям, необходимо выбрать подходящий язык программирования. Благодаря наличию ряда ключевых достоинств, в настоящее время широкую популярность получили объектно-ориентированные языки программирования, поддерживающие компонентную парадигму. C# – объектно-ориентированный язык программирования, относящийся к семье с С-подобным синтаксисом, из них его синтаксис наиболее близок к С++ и Java. Язык имеет статическую типизацию, поддерживает полиморфизм, перегрузку операторов, делегаты, атрибуты, события, свойства, обобщённые типы и методы и т.д. [5] Поскольку уже имелся опыт работы с C# выбор пал в его сторону, он также обусловлен следующими положениями: 1) Полная поддержка классов и объектно-ориентированного программирования, включая наследование интерфейсов и реализаций, виртуальных функций и перегрузки операторов; 2) Полный и хорошо определенный набор основных типов; 3) Встроенная поддержка автоматической генерации XML-документации, использование WPF; 4) Автоматическое освобождение динамически распределенной памяти; 5) Возможность отметки классов и методов атрибутами, определяемыми пользователем; 6) Полный доступ к библиотеке базовых классов .NET, а также легкий доступ к Windows API; [12] 7) Простое изменение ключей компиляции. Позволяет получать исполняемые файлы или библиотеки компонентов .NET, которые могут быть вызваны другим кодом так же, как элементы управления ActiveX; 3.2 Разработка задачи распределения ресурсов Для разработки интерфейса под задачу оптимального распределения ресурсов необходимо как минимум три входных переменных – Количество распределяемых ресурсов (resourceValue), Шаг распределения (resourceValueStep), Количество предприятий (companyCount). Для них созданы соответствующие TextBox, которые заполняет пользователи. Однако введены булевы переменные для каждого из них, если их значение false, то в каком-то из TextBox введены некорректные данные, выделив то самое значение красным цветом, что не позволяет создать таблицу с распределением инвестиций. При инициализации формы выполняется функция GenerateDataGrid, где таблица исходных данных автоматически формируется исходя из заданных параметров, причём все значения в ней целочисленные, ввод каких-либо символов или разделителей в ячейки недопустим. Создание происходит путем добавления столбца  , причем ему присваивается значение IsReadOnly. Затем для каждого филиала компании создается строка соответственно шагу распределения инвестиций вплоть до максимального значения. После создания ячеек DataGrid в свойстве ItemResource присваивается значение bindingData. , причем ему присваивается значение IsReadOnly. Затем для каждого филиала компании создается строка соответственно шагу распределения инвестиций вплоть до максимального значения. После создания ячеек DataGrid в свойстве ItemResource присваивается значение bindingData.Создаваемая таблица формируется динамически, то есть при изменении какого-либо из входных параметров при помощи функции TextChanged она создаётся по новой путём использования той же функции генерации. Затем создается блок вывода результатов, в нем расположена строка, в которую будет вписано максимальная прибыль при распределении ресурсов исходя из данных outputData, в который по нажатию на кнопку «Просчитать» вносится искомый результат функцией ProcessingData(). Но для начала создается класс Company, с полями необходимые для подсчёта рекуррентной формулы Беллмана, то есть это k – шаг оптимизации и значения предыдущих вычислений функции. Разработанная форма для задачи распределения ресурсов показана на рисунке 1. 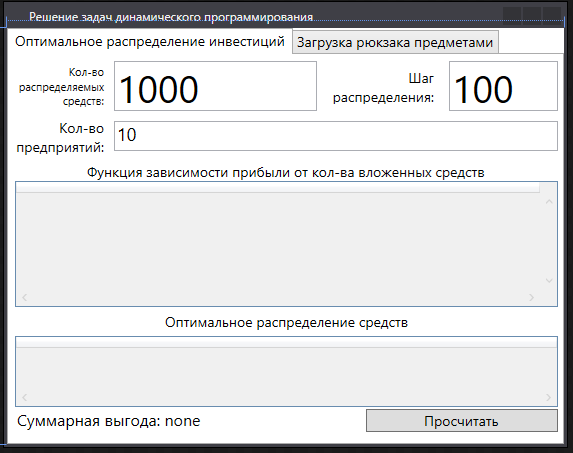 Рисунок 1 – форма задачи о распределении ресурсов Вычисления начинается с условной оптимизации, то есть с шага k = 1, каждой функции 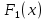 присваивается соответствующее значение при вложении средств x. Поиск присваивается соответствующее значение при вложении средств x. Поиск 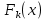 будет происходить до тех пор, пока шаг не будет равен значению CompanyCount, то есть количеству филиалов компаний. Для записи финального результат используется список FinalResults, содержащий в себе экземпляры класса Company, а для корректного вывода распределяемых средств используется класс VisualResults, содержащий в себе единственное поле – одномерный массив VisualHistory, хранящий в себе результаты работы программы. будет происходить до тех пор, пока шаг не будет равен значению CompanyCount, то есть количеству филиалов компаний. Для записи финального результат используется список FinalResults, содержащий в себе экземпляры класса Company, а для корректного вывода распределяемых средств используется класс VisualResults, содержащий в себе единственное поле – одномерный массив VisualHistory, хранящий в себе результаты работы программы.Подробнее и нагляднее этот алгоритм представлен в виде блок-схемы в Приложении А. Теперь необходимо провести тестирование программы, внеся исходные данные типовой задачи об оптимальном распределении ресурсов предприятия из раздела 2.1. Тестирование проведено успешно, расхождений не найдено результаты показаны на рисунке 2. Как и в ответе решенной задачи следует распределить средства инвестиций в размере 200 у.e. следующим образом: первому предприятию выделить 40 у.e., второму 80 у.e., третьему 40 у.e. и наконец четвертому 40 у.e., таким образом максимальная прибыль составит 24 у.e. 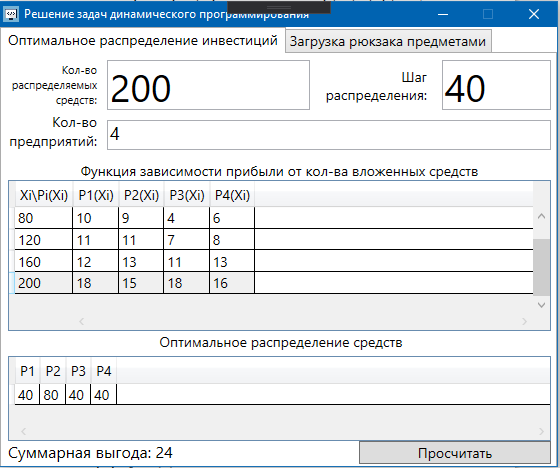 Рисунок 2 – тестирование на основе исходных данных 3.3 Разработка задачи о рюкзаке Для решения задачи о загрузке рюкзака предметами необходимо реализовать класс Backpack, полями которого являются: name – тип string, отвечает за название предмета; weight – тип int, вес предмета; price – тип int, цена предмета. Помимо этого, в классе реализован единственный конструктор по умолчанию с тремя входными параметрами, которые указаны выше. Затем следует спроектировать внешний вид этой задачи. Для ввода предметов в рюкзак будет использоваться такой элемент как DataGrid, которому в свойстве ItemSource присваивается класс Backpack через Binding, поскольку будут использоваться его поля для вывода списка предметов. После этого в DataGrid создаётся три столбца: Название, Вес (Wi), Цена (Pi). Источниками значений в этих столбцах соответственно будут значения экземпляра класса Backpack. При запуске приложения выполняется функция AddRanec(), которая формирует коллекцию экземпляров Backpack – items. Чтобы при запуске программы DataGrid не был пустым создается пустой экземпляр класса с параметрами – 0,0,0. Для добавления/удаления предметов, помещаемых в рюкзак, используются кнопки с соответствующим Content – «+», «  ». ». После создается поле, с которого будет считываться максимальная вместимость рюкзака и присваиваться переменной W. Для работы программы без сбоев для этого поля создана функция OnlyNumbers, которая позволяет вводить только цифры без использования разделителей или знака минус путем проверки значения IsDigit. Далее создается CheckBox с названием «Неограниченный рюкзак». Если его свойство IsChecked имеет значение true, это означает, что в рюкзак может быть любой предмет любое количество раз. Иначе решается классическая задача, когда любой предмет может быть взят некоторое количество раз. Созданный интерфейс для задачи о загрузке рюкзака предметами показана на рисунке 3 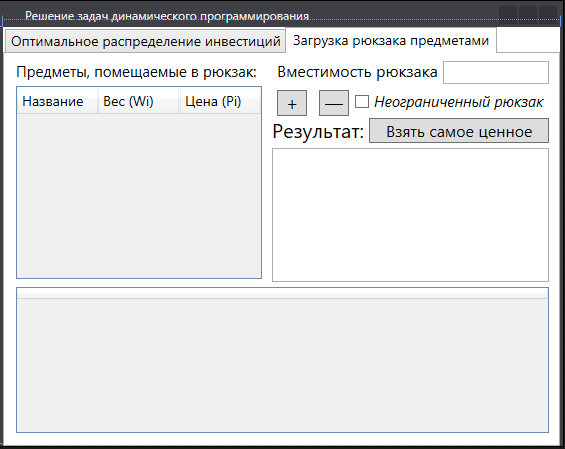 Рисунок 3 – Форма задачи о рюкзаке Теперь создается блок «Результат», он включает в себя DataGrid, находящийся в самом низу программы, который будет заполняться данными из полученного массива. Также TextBox, в который будут вноситься загруженные в рюкзак предметы, их номер, вес, стоимость. На новой строке записывается общий вес ранца, а еще полученная в результате работы программы максимальная стоимость рюкзака. Помимо вышеперечисленного в этом блоке расположена кнопка «Взять самое ценное», при нажатии на которую выполняется функция AlgorithmRanec(). Она находит рюкзак максимальной стоимости методом динамического программирования. Сначала из значений коллекции путём метода Select и преобразования ToArray() создаются массивы цен и весов введенных предметов p и w типа int соответственно. Переменной N присваивается следующее значение – w.Length – 1. Затем происходит создание двумерного массива и его заполнение согласно методу ДП, то есть значениям A[0,i] и A[i,0] присваиваются нули. После если вес текущего предмета меньше или равен значению текущего веса при переборе (то есть он вмещается), то проверяется условие стоит ли флажок напротив неограниченного рюкзака, если да, то A[k,s] присваивается максимальная стоимость текущего или предыдущего предметов. Происходит выбор: класть ли данный предмет в рюкзак? Иначе предмет в ранец не кладём. После заполнения массива в TextBox Result выводится максимальная стоимость рюкзака равная значению A[N,W]. Теперь происходит безусловная оптимизация, для этого создается лист типа int – Obj, содержащий в себе номера предметов, которые были положены в рюкзак. Затем следует условие, пока A[k,s] не равняется нулю, то происходит проверка: если стоимость текущего и предыдущего предметов совпадает, то k уменьшается на единицу. Иначе в Obj добавляется k, максимальный вес рюкзака уменьшается на вес предмета. Затем с конца листа Obj объекты присваиваются переменной j и, согласно его номеру, записываются в необходимой форме, причем переменной Total присваивается вес текущего предмета. После завершения цикла выводится получившийся вес рюкзака при загрузке его заданными предметами. Подробнее и нагляднее этот алгоритм представлен в виде блок-схемы в Приложении Б. Теперь необходимо провести тестирование программы, внеся исходные данные из задачи 2.2. Результаты успешного тестирования приведены на рисунке 4 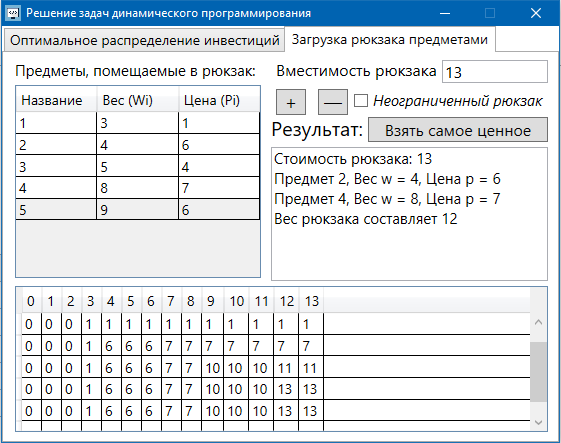 Рисунок 4 – тестирование задачи о рюкзаке Заключение По итогам написания курсового проекта достигнута цель – исследован метод динамического программирования и его применение для решения задач, соответственно решены поставленные задачи: 1) При помощи самостоятельного изучения интернет-ресурсов, дополнительной литературы получены знания о динамическом программировании, о постановке его общей задачи, а также об алгоритме решения. 2) Решены такие классические задачи как распределение ресурсов между предприятиями и загрузка рюкзака предметами методом динамического программирования, построены их математические модели. 3) Разработано приложение, позволяющее рассчитывать оптимальный план типовых задач динамического программирования. Проведено его успешное тестирование на основе исходных данных решенных задач, расхождений в расчётах не выявлено. Однако существует дальнейшая перспектива развития разработанной программы путем расширения списка задач, решаемых методом динамического программирования, добавление новых разновидностей формулировок уже осуществленных задач, реализация возможности выгрузки результатов работы программы в файл или заполнение таблиц исходными данными задачи из файла. Список использованных источников ГОСТ Р 7.0.5-2008 СИБИД. Библиографическая ссылка. Общие требования и правила составления. ГОСТ 7.32-2017 СИБИД. Отчет о научно-исследовательской работе. Структура и правила оформления. ГОСТ 19.701-90 Единая система программной документации. Схемы алгоритмов, программ, данных и систем. Обозначения условные и правила выполнения. Абрамян М.Э. Visual C# на примерах; БХВ-Петербург - М., 2016. - 436 c. Бабешко, Л. О. Математическое моделирование финансовой деятельности. Учебное пособие / Л.О. Бабешко. - М.: КноРус, 2016. - 224 c. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования; Главная редакция физико-математической литературы издательства "Наука" - М., 2016. - 458 c. Бродецкий, Г. Л. Экономико-математические методы и модели в логистике. Процедуры оптимизации / Г.Л. Бродецкий, Д.А. Гусев. - М.: Academia, 2017. - 288 c. Ватсон Б. С# 4.0 на примерах (C# 4.0. How-To); БХВ-Петербург - М., 2015. - 608 c. Галеев, Э. М. Оптимизация. Теория, примеры, задачи. Учебное пособие / Э.М. Галеев. - М.: Ленанд, 2015. - 344 c. Ишкова, Э. А. Самоучитель С#. Начала программирования / Э.А. Ишкова. - М.: Наука и техника, 2017. - 496 c. Калихман, И. Л. Динамическое программирование в примерах и задачах. Учебное пособие / И.Л. Калихман, М.А. Войтенко. - М.: Высшая школа, 2017. - 128 c. Лежнёв, А.В. Динамическое программирование в экономических задачах / А.В. Лежнёв. - М.: Бином. Лаборатория знаний, 2015. - 589 c. Ликнесс, Дж. Приложения для Windows 8 на C# и XAML / Дж. Ликнесс. - М.: Питер, 2015. - 368 c. Лугинин, О. Е. Экономико-математические методы и модели. Теория и практика с решением задач / О.Е. Лугинин, В.Н. Фомишина. - М.: Феникс, 2014. - 448 c. Окулов, С.М. Динамическое программирование / С.М. Окулов. - М.: Бином. Лаборатория знаний, 2015. - 598 c. Павловский, Ю. Н. Компьютерное моделирование. Учебное пособие / Ю.Н. Павловский, Н.В. Белотелов, Ю.И. Бродский. - М.: Физмат книга, 2014. - 304 c. Программирование, численные методы и математическое моделирование / И.Г. Семакин и др. - М.: КноРус, 2016. - 304 c. Приложение А (обязательное) Алгоритм решения задачи оптимального распределения ресурсов  Приложение Б (обязательное) Алгоритм решения задачи о загрузке рюкзака предметами 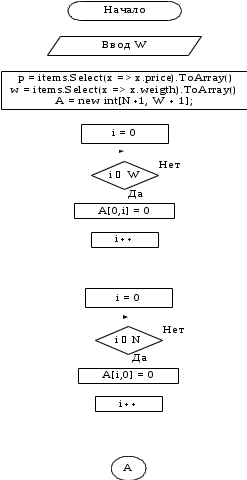  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

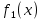
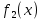
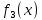
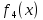
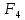 (x)
(x)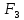 (x)
(x)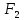 (x)
(x)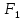 (x)
(x)