З.Си УП. 70. Курсовой проект по дисциплине здания, сооружения и их устойчивость при пожаре

• Название: Курсовой проект по дисциплине здания, сооружения и их устойчивость при пожаре
• Дата: 04.05.2022
• Размер: 3.49 Mb.
• Имя файла: З.Си УП. 70.docx
• Тип: Курсовой проект; #512467
• страница: 4 из 7

3. РАСЧЕТ ФАКТИЧЕСКОГО ПРЕДЕЛА ОГНЕСТОЙКОСТИ МЕТАЛЛИЧЕСКОЙ ФЕРМЫ ПОКРТЫИЯ

Высокая теплопроводность металла позволяет выполнить расчет стальных несущих конструкций по времени прогрева конструкции до критической температуры. Для каждого из элементов фермы следует определить величину критической температуры, то есть решить статическую задачу, а затем решить теплотехническую задачу по определению предела огнестойкости конструкции.

3.1. Статический расчет

Расчет растянутых элементов заданного узла фермы

Расчет производится из условия снижения прочности (предела текучести стали) до величины напряжения, возникающего в элементе от внешней (нормативной, рабочей) нагрузки).

Рассматриваем узел 17 (прил. 2, рис. 1). Растянутыми элементами (в соответствии с табл. 1 исходных данных) являются стержень Р4, Р5, Н2,Н3.

Расчет усилий, воспринимаемых элементом от нормативной нагрузки:

N_n(Р4=Р5) = N_(Р2) /γ_f = 207/1,2 = 172,5 кН;

N_n(Н2=Н3) = N_(Р2) /γ_f = 852/1,2 = 710 кН;

где N_(i) – расчетное усилие, воспринимаемое элементом фермы, Н;

γ_f – усредненное значение коэффициента надежности по нагрузке, равный 1,2.

Рассчитаем коэффициент изменения предела текучести стали, соответствующий критической температуре нагрева растянутого элемента фермы:

γ_{ytcr(Р4=Р5)} = N_{n(Pi) /} (A_(Pi) ⋅ R_yn) = 172,5*10³/(2*10,6*10^-4*245*10⁶) = 0,332;

γ_{ytcr(Н2=Н3)} = N_{n(Нi) /} (A_(Нi) ⋅ R_yn) = 710*10³/(2*15,2*10^-4*325*10⁶) = 0,719;

где А_(Р2) – площадь поперечного сечения элементов фермы, м², принимают с учетом количества профилей, на которые передается усилие от внешней нагрузки.

В узлах фермы каждый элемент выполнен из двух уголков (рис 3.1.1). Размеры уголка находятся в приложении 1, таблица 4.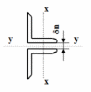


Рис. 3.1.1 Сечение элементов фермы

R_yny – нормативное сопротивление стали по пределу текучести определяется в зависимости от марки стали (приложение 1, таблица 3).

Несущая способность сжатых элементов исчерпывается при критических напряжениях, меньших, чем предел текучести. Это объясняется тем, что сжатые элементы теряют эксплуатационные качества не от разрушения сечения, а от потери устойчивости (выпучивания) стержня, поэтому сжатые элементы рассчитывают на устойчивость с учетом коэффициента φ (коэффициента продольного изгиба).
Расчет сжатых элементов заданного узла фермы

В связи с выше сказанным, расчет производится по потере устойчивости (выпучивания) сжатых элементов. Этот расчет можно провести по двум методикам:

• 
  Расчет элементов на устойчивость с учетом коэффициента продольного изгиба φ.
  
• 
  Из условия снижения модуля упругости стали до критической величины (что приводит к недопустимому прогибу элемента).
  

Сжатыми элементами (в соответствии с табл.3 исходных данных) являются стержни С4, Р4, Р5.
Расчет на устойчивость с учетом коэффициента продольного изгиба φ

Рассчитываем предел огнестойкости сжатых элементов фермы из условия устойчивости с учетом коэффициента продольного изгиба.

Определим гибкость в вертикальном направлении прогиба элементов фермы:

λ_x(С4) = l_x(С4) / i_x(С4) = 2468/27,8 = 88,78;

λ_x(P4=Р5) = l_x(Pi) / i_x(Pi) = 4271/27,8 = 153,63;

где l_x– расчетная длина элемента в вертикальном направлении прогиба (табл. 3.1.1), мм;

i_x – радиус инерции поперечного сечения элемента относительно оси «х» (приложение 1, таблица 4), мм.

Таблица 3.1.1

Расчетная длина элемента при его различных направлениях прогиба

Направление прогиба	Расчетная длина элемента, мм
	С4	Р4=Р5
Вертикальное	lx =0,8 l = 2468	lx= l = 4271
Горизонтальное	ly= l = 3085	ly= l = 4271

Определим гибкость в горизонтальном направлении прогиба элементов фермы:

λ_y(С4) = l_y(С4) / i_y(С4) = 3085/41,1 = 75,1;

λ_y(P4=Р5) = l_y(Pi) / i_y(Pi) = 4271/41,1 = 103,92;

где l_y– расчетная длина элемента в горизонтальном направлении прогиба (табл. 3.1.1), мм;

i_y – радиус инерции поперечного сечения элемента относительно оси «y» (приложение 1, таблица 4), мм.

Максимальная величина гибкости элемента фермы принимается равной наибольшей из гибкостей элемента в вертикальном и горизонтальном направлениях, то есть:

λ_max(С4) = 88,78;

λ_max(P4=Р5) = 153,63.

Коэффициент продольного изгиба φ элемента фермы принимается в зависимости от _max (если λ_max ≤ 40, то φ = 1; если λ_max > 40, то φ = 0,95) и равен:

для λ_max(С4) = 88,78> 40, φ_(С4) = 0,95;

для λ_max(P4=Р5) = 153,63> 40, φ_(P4=Р5) = 0,95;

Таким образом,

φ_(С4) = φ_(Р4) = φ_(Р5) = φ = 0,95

Усилия, воспринимаемые элементами от нормативной нагрузки, равны

N_n(С4) = N_(С4) /γ_f = 120/1,2 = 100 кН;

N_n(P4=Р5) = N_(P4=Р5) /γ_f = 120/1,2 = 100 кН;

Определим коэффициент изменения предела текучести стали при критической температуре нагрева сжатых элементов фермы из условия прочности с учетом коэффициента продольного изгиба:

γ_ytcr(С4) = N_n(С4)/ (A_(С4)* R_yn * φ) = 100*10³/(2 * 10,6* 10^-4 *245*10⁶ * 0,95) =
= 0,2;

γ_ytcr(P4=Р5) = N_n(P4=Р5)/(A_(P4=Р5)*R_yn*φ) = 100*10³/(2*10,6*10^-4*245*10⁶ *0,95)=
= 0,2.
Расчет из условия снижения модуля упругости стали до критической величины

Для расчета определим коэффициент изменения модуля упругости стали элементов фермы:

γ_е(С4) = (N_n(С4) ⋅ l²_(С4)) _/ (π² ⋅ E_n ⋅ J_min(С4)) = (100*10³*(3085*10^-3)²)/(3,14² *2,06* 10¹¹ *163,84* 10^-8) = 0,286;
γ_е(P4=Р5) = (N_n(P4=Р5) ⋅ l²_(P4=Р5)) _/ (π² ⋅ E_n ⋅ J_min(P4=Р5)) = (100* 10³ * (4271 * 10^-3)²)/(3,14² *2,06* 10¹¹* 163,84* 10^-8) = 0,548;
где π = 3,14;

E_n – нормативное значение модуля упругости стали, равное 2,06 ⋅ 10¹¹ Па;

J_min – миниальное значение момента инерции поперечного сечения элемента, м⁴, равное:

J_min(С4) = i_min(С4)² ⋅ 2A_(С4) = (2,78 ⋅ 10^-2)² ⋅ (2 ⋅ 10,6 ⋅ 10^-4) = 163,84 ⋅ 10^-8 м⁴;

J_min(Р4=Р5) = i_min(Р4=Р5)² ⋅ 2A_(Р4=Р5) = (2,78 ⋅ 10^-2)² ⋅ (2 ⋅ 10,6 ⋅ 10^-4) = 163,84 ⋅ 10^-8 м⁴.

где i_min – минимальное значение радиуса инерции поперечного сечения элемента из значений i_x и i_y, м, то есть:

i_min(С4) = 2,78 ⋅ 10^-2 м;

i_min(Р4=Р5) = 2,78 ⋅ 10^-2 м;

По графику (приложение 2, рисунок 5) определяем числовые значения критической температуры t_cr в зависимости от величин γ_ytcr и γ_e (для сжатых элементов). Полученные данные сведем в таблицу 3.1.2:

Таблица 3.1.2

Значения критической температуры t_cr в зависимости от величин γ_ytcr и γ_e

	Элементы фермы
	Растянутые				Сжатые
	Р4	Р5	Н2	Н3	Р4	Р5	С4
γytcr	0,332	0,332	0,719	0,719	0,2	0,2	0,2
γe	-	-	-	-	0,548	0,548	0,286
tcr, 0C по γytcr	610	610	390	390	660	660	660
tcr, 0C по γe	-	-	-	-	700	700	700

Результатом статической части расчета будут являться критические температуры рассматриваемых элементов конструкции, полученные по графику (приложение 2, рисунок 5).

Для теплотехнического расчета берутся минимальные значения t_cr, то есть:

t_cr(P4) = 610 ⁰C;

t_cr(P5) = 610 ⁰C;

t_cr(С4) = 660 ⁰C;

t_cr(Н2) = 390 ⁰C;

t_cr(Н3) = 390 ⁰C;