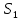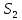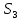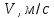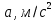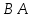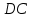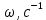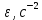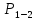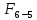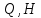Курсовой проект состоит из пяти листов графического материала, а также пояснительной записки
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
3.4. Кинематический анализ механизма методом графического дифференцирования Этим методом определяем величины скоростей, ускорений точки 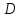 механизма. Сначала строим диаграмму перемещений ползуна « механизма. Сначала строим диаграмму перемещений ползуна «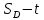 » в функции времени. Диаграммы « » в функции времени. Диаграммы «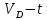 » и « » и «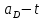 » строим методом графического дифференцирования соответственно диаграмм » строим методом графического дифференцирования соответственно диаграмм 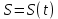 и и 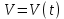 . Принимаем масштабный коэффициент . Принимаем масштабный коэффициент 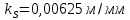 . .Время одного оборота кривошипа равно 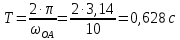 Вычислим масштабы: 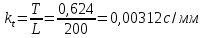 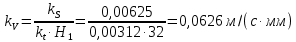 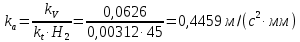 Для седьмого положения механизма по кинематическим диаграммам: 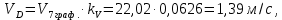 где 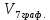 – ордината графика – ордината графика 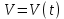 в точке 7. в точке 7.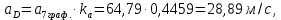 где 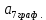 – ордината графика « – ордината графика «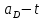 » в точке 7. » в точке 7.Скорости и ускорения точек и звеньев механизма в рассматриваемом положении механизма приведены в табл. 3.1., табл. 3.2. Табл. 3.1. Скорости и ускорения точек механизма в положении 4
По кинетическим диаграммам 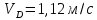 , , 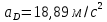 Погрешность от определения скорости точки 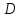 различными методами составляет 25 % различными методами составляет 25 %Погрешность от определения ускорения точки 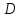 различными методами составляет 25,83% различными методами составляет 25,83%Табл. 3.2. Угловые скорости и ускорения звеньев механизма в положении 4
4. Кинетостатический анализ механизма Целью силового анализа является определение сил, действующих на звенья механизма, реакций в кинематических парах и уравновешивающей силы. В курсовом проекте задача силового расчета решается в первом приближении, предполагая, что трение в кинетических парах отсутствует. 4.1. Определение сил, действующих на звенья механизма Силы тяжести звеньев: 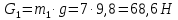 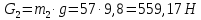 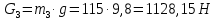 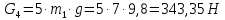 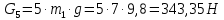 Сила сопротивления перемещению ползуна, направленная в противоположную сторону скорости 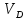 : :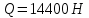 Величины сил инерции: 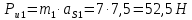 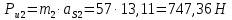 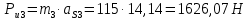 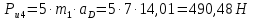 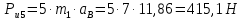 Эти силы прикладываем к центрам тяжести соответствующих звеньев и направляем в сторону, противоположную вектору ускорений центра тяжести. Моменты от сил инерции звеньев: 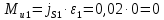 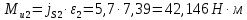 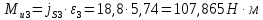 4.2. Определение реакций в кинематических парах Силовой расчет механизма начинается с группы Ассура 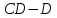 , наиболее удалённой от входного звена , наиболее удалённой от входного звена 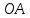 . На звенья этой группы действуют известные по величине и направлению силы веса . На звенья этой группы действуют известные по величине и направлению силы веса 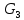 и и 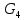 , силы инерции , силы инерции 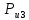 и и 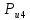 , момент , момент 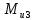 от силы инерции, технологическое усилие от силы инерции, технологическое усилие 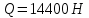 . .Эту группу Ассура освобождаем от связей и вместо них прикладываем к паре 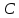 реакцию реакцию 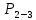 , а к паре , а к паре 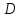 реакцию реакцию 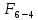 . Обе реакции неизвестны по величине. Реакция . Обе реакции неизвестны по величине. Реакция 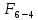 направлена направлена 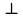 направляющей направляющей 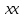 ползуна ползуна 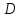 . Реакция . Реакция 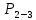 неизвестна по направлению. неизвестна по направлению.Реакцию 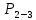 раскладываем на 2 взаимно перпендикулярные составляющие: раскладываем на 2 взаимно перпендикулярные составляющие: 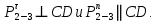 Запишем уравнение моментов всех сил, действующих на звено 3, относительно точки 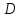 : :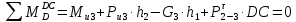 , отсюда , отсюда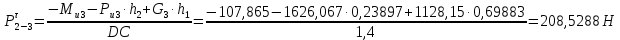 Далее, приняв масштаб сил 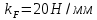 , строим план сил по векторному уравнению: , строим план сил по векторному уравнению: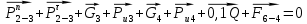 Из плана сил находим величины и направления сил 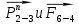 , а также полную реакцию в паре с , а также полную реакцию в паре с 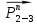 ( (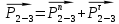 ). ).Переходим к силовому расчету группы Ассура 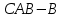 . Освобождаем от связей и прикладываем реакции . Освобождаем от связей и прикладываем реакции 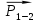 и и 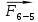 , которые неизвестны ни по величине, ни по направлению. , которые неизвестны ни по величине, ни по направлению.Реакцию 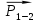 раскладываем на 2 взаимно перпендикулярные составляющие: раскладываем на 2 взаимно перпендикулярные составляющие: 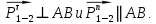 Запишем уравнение моментов всех сил, действующих на звено 2, относительно точки 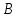 : :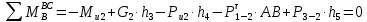 , отсюда , отсюда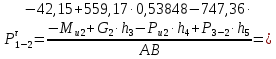 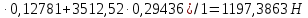 Задавшись масштабом 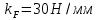 , строим план сил по векторному уравнению: , строим план сил по векторному уравнению: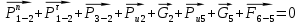 Из плана сил находим величины и направления сил 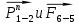 , а также полную реакцию в паре , а также полную реакцию в паре 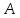 : ( : (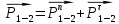 ). ).4.3. Силовой расчет входного звена механизма Для определения реакции 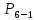 в кинематической паре, образованной входным звеном и стойкой, необходимо привести в равновесие все силы, действующие на это звено с учетом уравновешивающей силы. Уравновешивающая сила является реальной внешней силой, которая представляет собой действие привода на звено в кинематической паре, образованной входным звеном и стойкой, необходимо привести в равновесие все силы, действующие на это звено с учетом уравновешивающей силы. Уравновешивающая сила является реальной внешней силой, которая представляет собой действие привода на звено 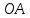 . .Величину уравновешивающей силы находим из уравнения моментов относительно точки 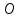 всех сил, действующих на звено 1: всех сил, действующих на звено 1: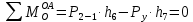 , отсюда , отсюда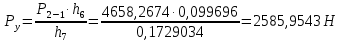 Для определения численного значения 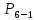 строим план сил в масштабе строим план сил в масштабе 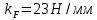 согласно векторному уравнению: согласно векторному уравнению: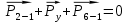 Результаты силового расчёта с использованием планов сил указаны в табл. 4.1. Табл. 4.1. Реакции в кинематических парах рычажного механизма для положения 4, Н
4.4. Определение уравновешивающей силы методом Н.Е. Жуковского Чтобы найти уравновешивающую силу методом Н.Е. Жуковского построим план скоростей и в соответствующие точки этого плана перенесём все силы (внешние и инерции), действующие на звенья механизма, предварительно повернув их в одном направлении на угол 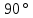 . .Моменты сил инерции заменяем парами сил: 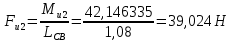 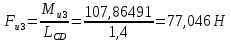 Рассматривая план скоростей как жёсткий рычаг, который находится в равновесии, определим сумму моментов всех сил относительно полюса: 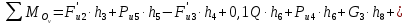 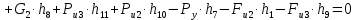 Выражаем из этого уравнения 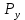 : :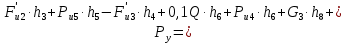 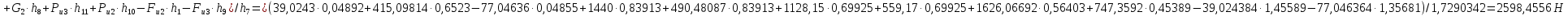 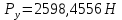 Погрешность в расчётах уравновешивающей силы разными способами составляет: 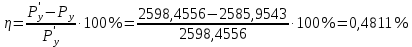 5. Динамический расчет механизма Внутри цикла установившегося движения угловая скорость начального звена машины периодически меняется из-за постоянного изменения нагрузок, что приводит к нежелательной неравномерности движения. Неравномерность движения начального звена характеризуется коэффициентом неравномерности движения 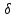 , который не должен превышать допускаемого значения , который не должен превышать допускаемого значения 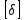 . Для снижения колебаний угловой скорости начального звена до допустимых пределов в машине предусматривают маховик, который с целью уменьшения его размеров устанавливают на быстроходном валу. Задачей динамического расчета механизма является определение расхода мощности и основных геометрических размеров маховика по заданному коэффициенту . Для снижения колебаний угловой скорости начального звена до допустимых пределов в машине предусматривают маховик, который с целью уменьшения его размеров устанавливают на быстроходном валу. Задачей динамического расчета механизма является определение расхода мощности и основных геометрических размеров маховика по заданному коэффициенту 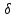 неравномерности хода машины. неравномерности хода машины. 5.1. Приведение сил, построение диаграммы работ и их разностей С использованием диаграммы силы сопротивления, действующей на ползун 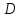 , изображаем на соответствующем листе проекта график характеристики технологической силы от положения механизма. Определяем численные значения силы сопротивления по формуле , изображаем на соответствующем листе проекта график характеристики технологической силы от положения механизма. Определяем численные значения силы сопротивления по формуле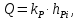 где 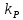 – масштаб диаграммы сил; – масштаб диаграммы сил; 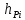 – ордината диаграммы для данного положения механизма. – ордината диаграммы для данного положения механизма.Численные значения силы сопротивления указываем в табл. 5.1. Приведение сил для  -го положения механизма по методу Жуковского осуществляется по формуле: -го положения механизма по методу Жуковского осуществляется по формуле: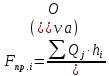 Здесь 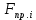 – приведенная сила; – приведенная сила; 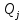 – активная сила, приложенная к звену – активная сила, приложенная к звену 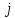 ; ;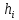 - плечо этой силы в плане скоростей относительно его полюса; - плечо этой силы в плане скоростей относительно его полюса;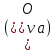 – графическое изображение скорости точки приведения (пальца кривошипа) на плане скоростей. – графическое изображение скорости точки приведения (пальца кривошипа) на плане скоростей. Табл. 5.1. Внешняя сила, действующая на ползун 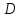
Момент приведенной силы, или приведенный момент 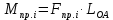 где 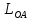 – удаление точки приведения от оси вращения начального звена (длина кривошипа). – удаление точки приведения от оси вращения начального звена (длина кривошипа).Для седьмого положения механизма: 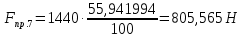 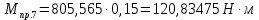 Поскольку цикл машины соответствует одному обороту ведущего звена, то приведенные силы и их моменты отыскиваем для двенадцати положений механизма. В соответствии с результатами расчета на чертежном листе строим диаграмму приведенных моментов в функции угла 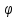 поворота кривошипа. поворота кривошипа.Численные значения приведённых сил и приведённых моментов сил сопротивления указаны в табл. 5.2. В седьмом положении механизма приведенный момент изобразим на диаграмме « 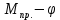 » отрезком » отрезком 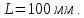 Масштаб приведенных моментов на диаграмме « Масштаб приведенных моментов на диаграмме «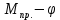 » »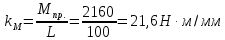 Масштаб угла поворота начального звена (кривошипа) 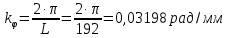 Путем графического интегрирования диаграммы приведенных моментов строим диаграмму работ заданных сил сопротивления 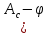 ) за цикл. На этом же графике строится диаграмма работ движущихся сил. При этом предполагается, что приведенный движущийся момент есть величина постоянная. Следовательно, работа этого момента будет выражаться прямолинейной зависимостью в системе координат « ) за цикл. На этом же графике строится диаграмма работ движущихся сил. При этом предполагается, что приведенный движущийся момент есть величина постоянная. Следовательно, работа этого момента будет выражаться прямолинейной зависимостью в системе координат «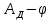 ». ». Таблица 5.2. Приведение силы и их моменты сил сопротивления
При установившемся движении за цикл справедливо равенство 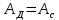 , поэтому в начале и в конце цикла ординаты , поэтому в начале и в конце цикла ординаты 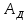 и и 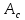 будут одинаковы между собой по абсолютной величине, а прямая, выражающая работу движущихся сил, соединит начало координат с концом графика « будут одинаковы между собой по абсолютной величине, а прямая, выражающая работу движущихся сил, соединит начало координат с концом графика «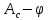 ». ».Масштаб диаграммы работ: 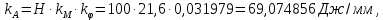 где 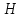 – это полюсное расстояние при графическом интегрировании. – это полюсное расстояние при графическом интегрировании.Расход мощности за цикл, т.е. средняя мощность без учета потерь трения в приводе, равен 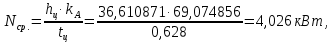 где 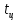 – время цикла; – время цикла; 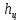 - ордината графика « - ордината графика «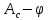 », соответствующая концу цикла. », соответствующая концу цикла.На полученной диаграмме работ ординаты поля между криволинейным графиком, изображающим работу сил сопротивления, и прямолинейным, отображающим работу движущих сил, будут определять собой разность работ, или приращение кинетической энергии машины. Замеряя разность ординат 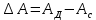 для каждого положения механизма, строим диаграмму разности работ – диаграмму приращения кинетической энергии. для каждого положения механизма, строим диаграмму разности работ – диаграмму приращения кинетической энергии. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||