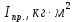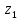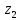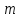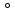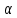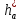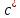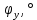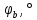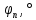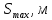Курсовой проект состоит из пяти листов графического материала, а также пояснительной записки
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
5.2. Приведение моментов инерции Приведенный момент инерции определяется для каждого положения механизма по формуле 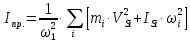 Для рассматриваемого положения механизма 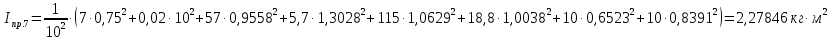 Результаты расчётов приведённых моментов инерции указаны в табл. 5.3. Пользуясь данными табл. 5.3, строим диаграмму приведенных моментов инерции звеньев в функции угла поворота кривошипа, отобразив величину  отрезком отрезком  . Масштаб диаграммы приведенных моментов инерции: . Масштаб диаграммы приведенных моментов инерции: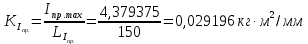 Табл. 5.3. Приведенные моменты инерции механизма
5.3. Расчет маховика Момент инерции маховика и его масса зависят от его местоположения в кинематической цепи механизма. Чем выше частота вращения вала, на котором установлен маховик, тем меньше его размеры при вычисленном моменте инерции группы звеньев, обеспечивающем движение начального звена с номинальной средней угловой скоростью и заданным коэффициентом 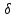 неравномерности движения. неравномерности движения.Определяем углы 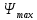 и и 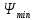 по выражениям: по выражениям: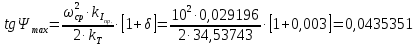 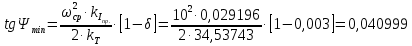 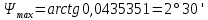 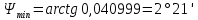 С использованием данных диаграммы разности работ « 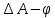 » и диаграммы приведённых моментов инерции « » и диаграммы приведённых моментов инерции «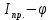 » строим диаграмму кинетической энергии в функции приведённого момента инерции « » строим диаграмму кинетической энергии в функции приведённого момента инерции «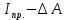 » – диаграмму Виттенбауэра. К полученной замкнутой кривой проводим наклонённые к оси абсцисс две касательные: снизу под углом » – диаграмму Виттенбауэра. К полученной замкнутой кривой проводим наклонённые к оси абсцисс две касательные: снизу под углом 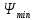 к оси абсцисс и сверху под углом к оси абсцисс и сверху под углом  . Касательные пересекают ось ординат в точках . Касательные пересекают ось ординат в точках 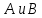 . .Приведённый момент инерции маховика: 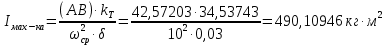 Средний диаметр обода маховика: 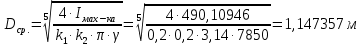 Принимаем: 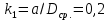 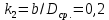 Здесь 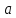 и и 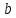 – размеры поперечного сечения обода маховика; – размеры поперечного сечения обода маховика;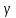 – плотность материала маховика, – плотность материала маховика, 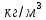 . .Определив 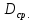 , находим , находим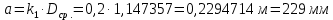 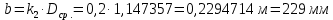 6. Синтез эвольвентного зубчатого зацепления Для синтеза зубчатого зацепления используются следующие данные, имеющиеся в задании: Числа зубьев колес: 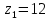 ; ; 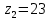 ; модуль ; модуль 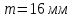 . .Угол профиля инструментальной рейки 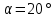 ; коэффициент высоты зуба ; коэффициент высоты зуба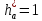 ; коэффициент радикального зазора ; коэффициент радикального зазора 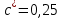 . .Коэффициенты смещения исходного производящего контура 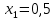 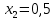 Исходные данные для синтеза приведены в таблице 6.1. Табл. 6.1 Исходные данные для синтеза
6.1. Геометрические параметры зацепления Радиусы делительных окружностей: 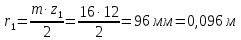 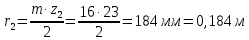 Радиусы основных окружностей: 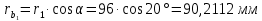 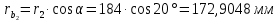 Длительный окружной шаг: 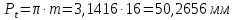 Делительная окружная толщина зуба: 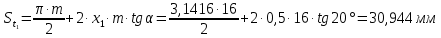 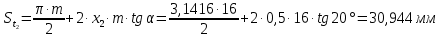 Угол зацепления: 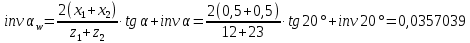 По таблице находим: 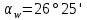 Межосевое расстояние: 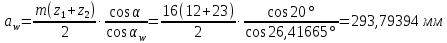 Радиусы начальных окружностей: 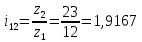 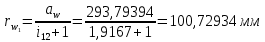 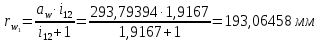 Радиусы окружностей впадин: 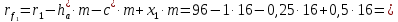 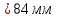 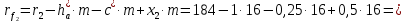 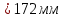 Радиусы окружностей вершин: 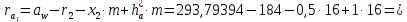 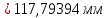 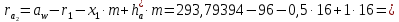 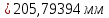 Шаг по основной окружности (основной шаг): 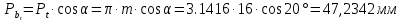 Углы профилей зубьев колес по окружностям вершин зубьев (градусы): 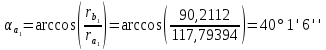 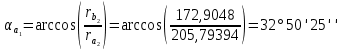 Найдем инволюты углов 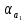 и и 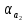 : :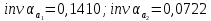 Толщина зуба по окружности вершин, мм: 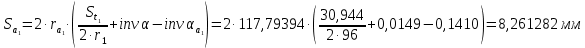 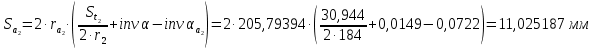 Об отсутствии заострения зубьев свидетельствует неравенства: 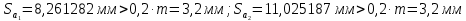 6.2. Построение картины внешнего эвольвентного зацепления 1. Строим начальные окружности с радиусами 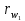 и и 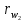 . В точке соприкосновения этих окружностей получаем точку . В точке соприкосновения этих окружностей получаем точку 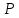 – полюс зацепления. – полюс зацепления.2. Проводим касательную 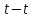 к этим окружностям через полюс к этим окружностям через полюс 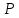 . .3. Поворачиваем касательную 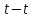 на угол на угол 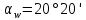 против часовой стрелки относительно точки против часовой стрелки относительно точки 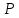 и получаем прямую и получаем прямую 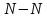 . .3. Проводим перпендикуляры к прямой 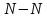 через центры начальных окружностей и получаем точки через центры начальных окружностей и получаем точки 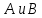 . . 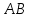 – теоретическая линия зацепления. – теоретическая линия зацепления.4. Строим эвольвентные профили зубьев, перекатывая линию 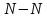 по основным окружностям. по основным окружностям.5. Проводим окружности вершин зубьев с радиусами 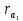 и и 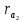 . .6. Проводим окружности впадин 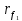 и и 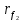 . .7. Строим профили зубьев. 8. Отмечаем практическую линию зацепления 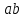 , лежащую на линии , лежащую на линии 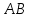 между окружностями вершин колёс. между окружностями вершин колёс.6.3. Качественные показатели зацепления 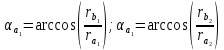 Коэффициент прикрытия: 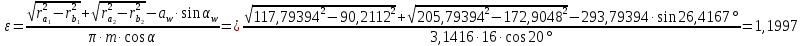 Относительная скорость скольжения: 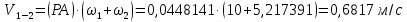 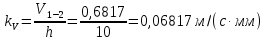 Коэффициенты удельного скольжения 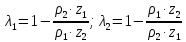 При входе в зацепление в точке 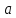 практической линии зацепления: практической линии зацепления: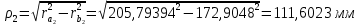 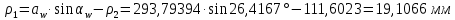 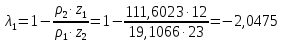 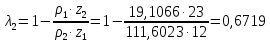 При выходе из зацепления в точке 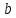 : :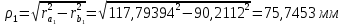 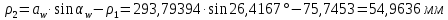 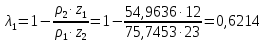 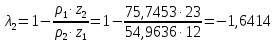 Масштабный коэффициент, принимаемый при построении диаграммы коэффициентов удельного скольжения: 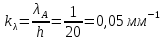 7. Синтез кулачковых механизмов Синтез кулачкового механизма заключается в определении основных размеров механизма и профиля кулачка по заданному движению толкателя. Исходные данные для синтеза кулачкового механизма приведены в табл. 7.1. Табл. 7.1. Исходные данные для синтеза кулачкового механизма
В нашем случае кулачковый механизм с плоским толкателем. 1. В произвольном масштабе вычерчиваем диаграмму аналогов ускорений толкателя в функции угла поворота кулачка « 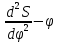 ». ».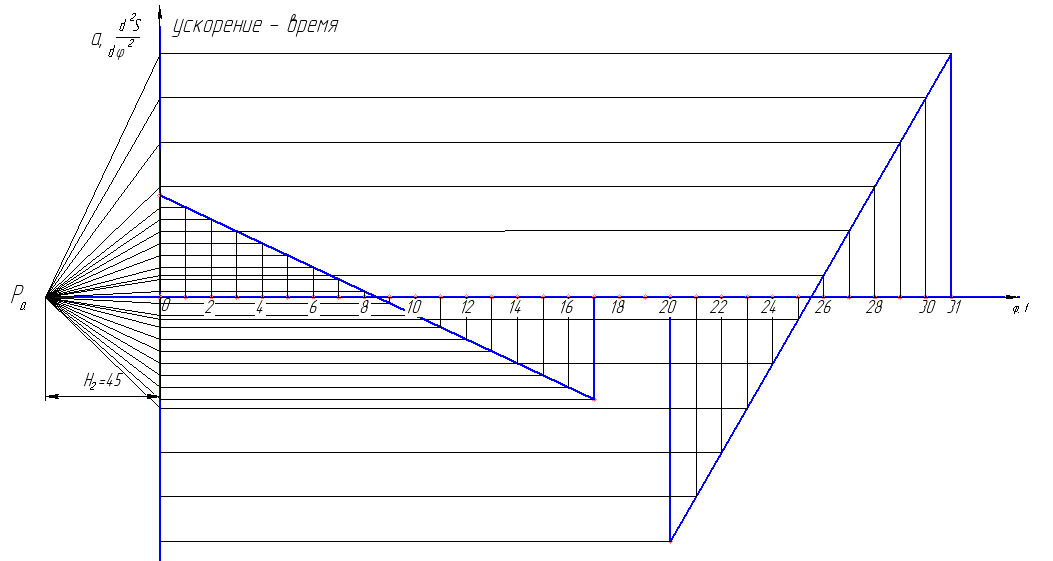 Рис. 7.1. Диаграмма аналогов ускорений толкателя 2. Методом графического интегрирования диаграммы аналогов ускорений строим диаграмму аналогов скорости « 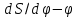 » и диаграмму перемещения толкателя « » и диаграмму перемещения толкателя «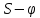 » в зависимости от угла поворота кулачка » в зависимости от угла поворота кулачка 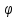 . .3. Определяем масштабы построенных диаграмм: Масштаб угла поворота по оси абсцисс: 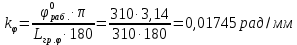 Здесь 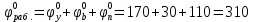 – угол рабочего профиля кулачка и его составляющие при удалении – угол рабочего профиля кулачка и его составляющие при удалении 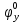 ; дальнем состоянии ; дальнем состоянии 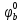 и сближении и сближении 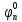 . .Масштаб перемещения толкателя определяется исходя из максимальной ординаты 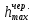 диаграммы « диаграммы «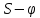 ». ».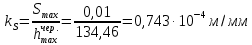 Масштаб диаграммы аналогов скоростей: 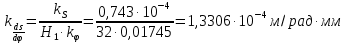 Масштаб диаграммы аналогов ускорений: 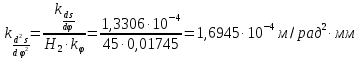 4. Определяем положение центра вращения и минимального радиуса-вектора теоретического профиля кулачка. Строим диаграмму « 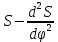 », при соблюдении условия: », при соблюдении условия: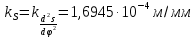 К полученной кривой проводятся касательные под углом 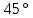 к оси к оси 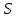 . Расстояние от начала координат диаграммы « . Расстояние от начала координат диаграммы «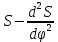 » до точки пересечения касательной с осью ординат равно » до точки пересечения касательной с осью ординат равно 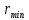 – минимальному радиус-вектору теоретического профиля кулачка. – минимальному радиус-вектору теоретического профиля кулачка.5. Профилирование кулачка методом обращенного движения. Всем звеньям механизма условно сообщается вращение с угловой скоростью, равной скорости кулачка, но противоположно направленной. При этом кулачок условно неподвижен, а стойка вращается относительно центра вращения кулачка совместно с толкателем. Движение толкателя относительно профиля кулачка в действительном и обращённом движении одинаково. В каждом положении толкатель перемещается на заданное расстояние 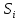 от нулевого положения и поворачивается вместе со стойкой в обращенном движении на угол от нулевого положения и поворачивается вместе со стойкой в обращенном движении на угол 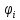 . Построив все положения тарелки толкателя, строим огибающую к тарелкам, которая и является искомым профилем кулачка. . Построив все положения тарелки толкателя, строим огибающую к тарелкам, которая и является искомым профилем кулачка.Заключение 1. Выполнен структурный анализ механизма. Выявлены основные особенности и разновидности групп Ассура, состав и последовательность присоединений структурных групп. 2. Найдены положения звеньев механизма и траектории отдельных точек. Решены задачи определения линейных скоростей и ускорений точек, а так же угловых скоростей и ускорений. 3. Получены реакции в кинематических парах. Найдена величина уравновешивающего момента. 4. Реализован переход от многозвенного механизма к его одномассовой модели. Определены параметры механизма, обеспечивающие заданный коэффициент неравномерности движения. Получена предварительная оценка величины средней мощности, необходимой для определения сил сопротивления движению механизмов. На неравномерность движения начального звена основное влияние оказывает технологическая нагрузка. 5. Определены геометрические параметры показателей качества зубчатой передачи. Проанализировано взаимодействие сопряженных профилей. Анализ зацепления даёт основание утверждать, что наибольший износ поверхности зубьев имеет место у основания ножек. 6. Спроектированы кулачковые механизмы, обеспечивающие заданные законы движения толкателя при выполнении обязательных и желательных условий синтеза. Библиографический список 1. «Теория механизмов и машин: методические указания для выполнения курсового проекта». Составители Э. А. Бубнов, А. Г. Черненко: ГОУ ВПО УГТУ-УПИ. Екатеринбург, 2006. 2. «Теория механизмов и машин: конспект лекций». В. И. Соколовский. Изд. УПИ. Свердловск, 1971. 3. «Курсовое проектирование по теории механизмов и машин». А. С. Кореняко, Л. И. Кременштейн, С. Д. Петровский, Г. М. Овсиенко, В. Е. Баханов. Изд. «Машиностроение». Москва, 1964. 4. «Теория механизмов и машин. Кинематика, динамика и расчёт». Ю. Ф. Лачуга, А. Н. Воскресенский, М. Ю. Чернов. Изд. «КолосС». Москва, 2007. |