Курсовой проект состоит из пяти листов графического материала, а также пояснительной записки
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Содержание
Введение Темой курсового проекта является кинематический и динамический анализ, а также синтез механизмов двухпозиционного пресса. Курсовой проект состоит из пяти листов графического материала, а также пояснительной записки. Необходимо выполнить структурный анализ механизма. Выявить основные особенности и разновидности групп Ассура, состав и последовательность присоединений структурных групп, работоспособность механизма. Выполнить кинематический анализ механизма, т.е. найти положения звеньев механизма и траектории отдельных точек. Определить линейные скорости и ускорения точек, а также значения угловых скоростей и ускорений звеньев механизма. Провести кинетостатический анализ механизма. Определить силы, действующие на звенья механизма. Получить реакции в кинематических парах. Провести силовой расчет входного звена механизма. Определить уравновешивающую силу методом Жуковского. Выполнить синтез эвольвентного зубчатого зацепления. Определить геометрические параметры показателей качества зубчатой передачи. Проанализировать взаимодействие сопряженных профилей. Сделать анализ зацепления. Спроектировать кулачковый механизм с поступательно перемещающимся плоским толкателем, обеспечивающий заданные законы движения толкателя. Сделать динамический расчёт. Определить расход мощности и основные геометрические размеры маховика. Исходные данные варианта 1 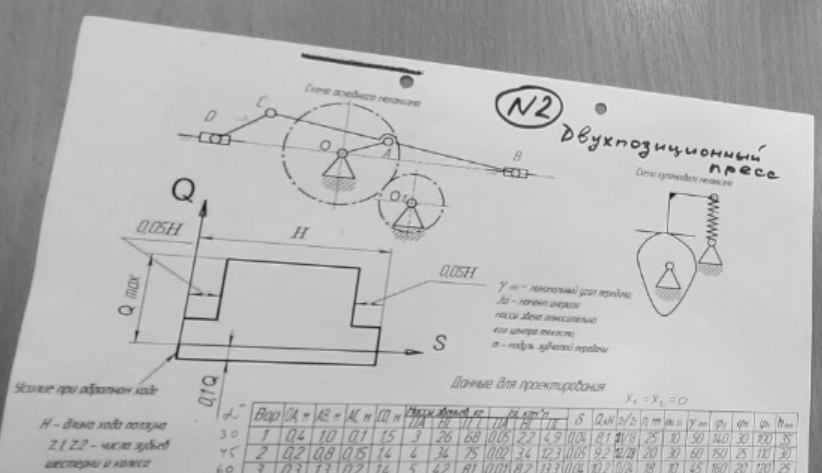 1. Задание на проектирование Кинематическая схема рычажного механизма показана на рис. 1.1. Диаграмма технологической силы, действующей на ползун  , изображена на рис. 1.2. Размеры и массы звеньев механизма указаны в табл. 1.1. , изображена на рис. 1.2. Размеры и массы звеньев механизма указаны в табл. 1.1. Р  ис. 1.1. Кинематическая схема рычажного механизма Рис. 1.2. Диаграмма силы сопротивления, действующей на ползун 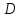 Табл. 1.1. Исходные данные для проекта
Задаются также: - кинематическая схема зубчатого механизма, числа зубьев и модуль зубчатых колес; - кинематическая схема, фазовые углы поворота кулачка и диаграмма аналога ускорения толкателя кулачкового механизма. 2. Структурный анализ рычажного механизма Кинематическая схема рычажного механизма показана на рис. 1.1. Механизм плоский рычажный. Для этого механизма: 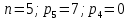 Степень подвижности плоского механизма определяется по формуле П.Л. Чебышева: 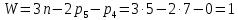 , где , где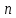 - число подвижных звеньев; - число подвижных звеньев;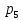 – число пар пятого класса; – число пар пятого класса; 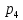 – число пар четвертого класса. – число пар четвертого класса.Согласно полученному результату для определенности движения всех звеньев механизма необходимо иметь одно входное звено. Разложение механизма на группы Ассура показано на рис. 2.1. 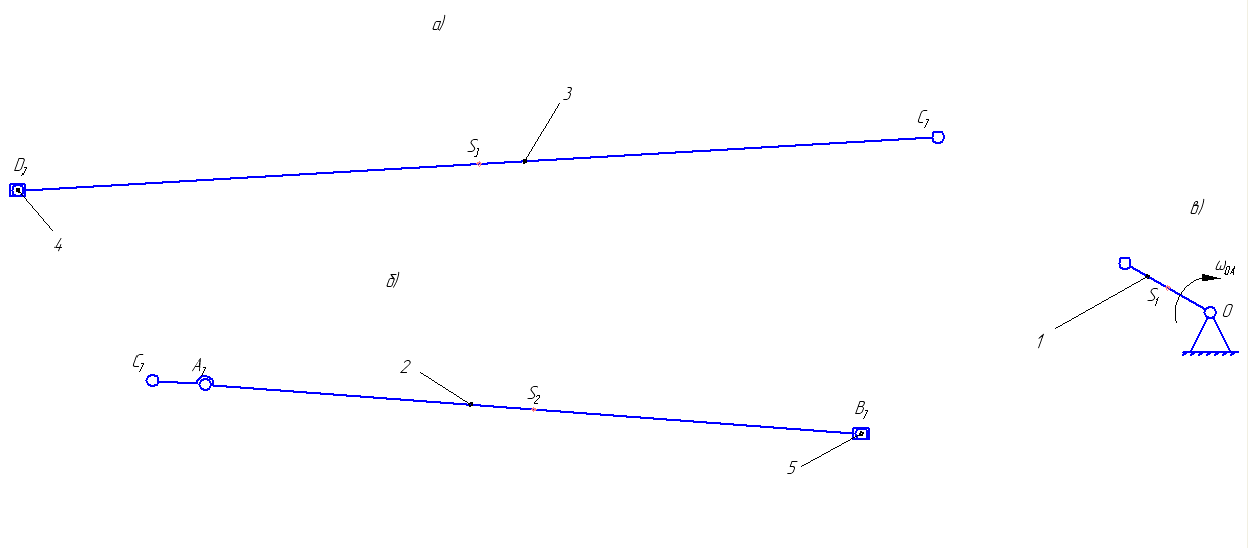 Рис. 2.1. Строение механизма а) группа Асура 2-го класса, 2-го вида, 2-го порядка; б) группа Асура 2-го класса, 2-го вида, 2-го порядка; в) механизм 1-го класса или группа начальных звеньев. Определим степень подвижности каждой группы в отдельности: а) группа Асура 2-го класса, 2-го вида: 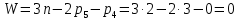 б) группа Асура 2-го класса, 2-го вида: 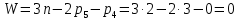 в) механизм 1-го класса: 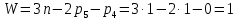 Вывод: рассматриваемый механизм является механизмом 2-го класса. 3. Кинематический анализ рычажного механизма. Целью кинематического анализа является установление положений звеньев механизма, определение скоростей и ускорений его звеньев. 3.1. Построение положений звеньев Задача о положениях звеньев решается на первом листе проекта графически путем построения кинематической схемы механизма в двенадцати положениях механизма. На плане механизма отобразим входное звено  отрезком длиной отрезком длиной  мм. мм.Масштабный коэффициент планов механизма: 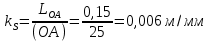 3.2. Определение скоростей звеньев механизма Рассмотрим 7-е положение механизма. Скорость точки 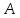 : :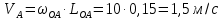 Скорости остальных точек механизма находим путем построения плана скоростей. Принимаем длину отрезка 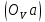 , изображающего скорость , изображающего скорость 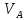 точки точки 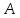 , равной 100 мм. , равной 100 мм.Тогда масштабный коэффициент плана скоростей:  Рассматривая движение точки  вместе с точками вместе с точками  и и 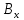 и относительно этих точек, получим векторные уравнения для построения скорости точки: и относительно этих точек, получим векторные уравнения для построения скорости точки: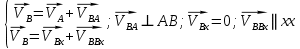 Величина (модуль) скорости точки 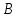 : :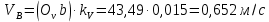 Используя принцип подобия, найдём расстояние 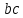 на плане скоростей: на плане скоростей: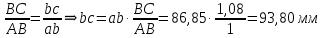 Скорость точки 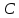 : :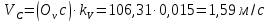 Векторные уравнения для нахождения скорости точки 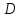 следующий вид: следующий вид: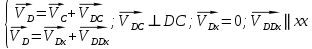 Скорость точки 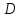 : :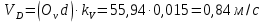 Определение скоростей центров тяжести звеньев производится с помощью теоремы подобия: 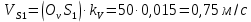 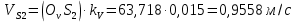 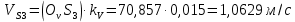 Определение угловых скоростей звеньев: 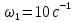 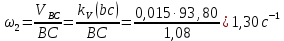 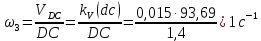 Направления угловых скоростей определяем по относительной линейной скорости. 3.3. Определение ускорений точек звеньев механизма Ускорение точки 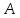 : :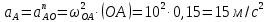 В общем случае: 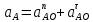 , но так как , но так как 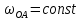 , то , то 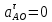 , поэтому , поэтому 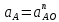 . .Принимаем длину отрезка 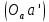 , изображающего вектор ускорения точки , изображающего вектор ускорения точки 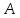 , равной , равной 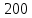 мм. Тогда масштабный коэффициент плана ускорений: мм. Тогда масштабный коэффициент плана ускорений: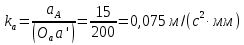 Рассматривая движение точки 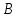 вместе с точками вместе с точками 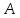 и и 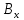 и относительно этих точек, получим векторные уравнения для построения ускорения точки: и относительно этих точек, получим векторные уравнения для построения ускорения точки: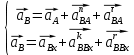 Первое уравнение: 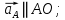 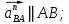 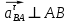 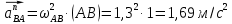 Графическое изображение вектора нормального ускорения 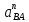 на плане ускорений равное отрезку на плане ускорений равное отрезку 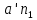 определяется по формуле: определяется по формуле: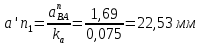 Второе уравнение: 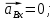 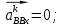 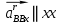 Величина (модуль) ускорения точки 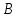 : :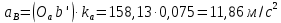 Используя принцип подобия, найдём расстояние 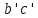 на плане ускорений: на плане ускорений: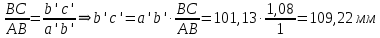 Абсолютное ускорение точки 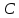 : :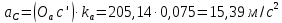 Векторные уравнения для нахождения ускорения точки 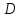 : :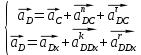 Первое уравнение: 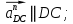 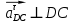 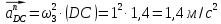 Графическое изображение вектора нормального ускорения 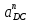 на плане ускорений равное отрезку на плане ускорений равное отрезку 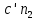 определяется по формуле: определяется по формуле: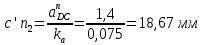 Второе уравнение: 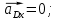 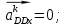 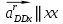 Величина (модуль) ускорения точки 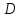 : :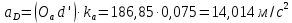 Определение ускорений центров тяжести звеньев производится с помощью теоремы подобия: 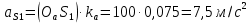 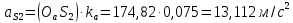 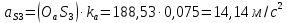 Определение угловых ускорений звеньев механизма: Угловое ускорение звена 1 равно 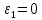 , так как , так как 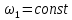 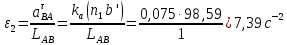 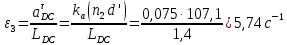 Направление углового ускорения 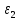 определяем по направлению вектора определяем по направлению вектора 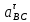 , перенесенного в точку , перенесенного в точку 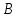 . Угловое ускорение . Угловое ускорение 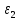 направлено против направлении вращения стрелки часов. Направление угловых ускорений остальных звеньев отыскиваются аналогично. направлено против направлении вращения стрелки часов. Направление угловых ускорений остальных звеньев отыскиваются аналогично. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

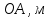
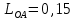
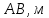
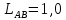
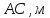
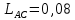
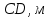
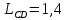
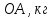
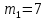
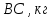
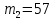
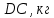
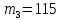
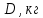
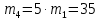
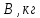
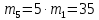
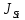 относительно их центров тяжести,
относительно их центров тяжести, 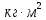 .
.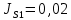
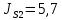
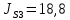
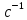
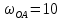
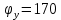
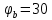
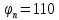
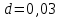
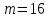
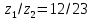
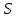 , расположены на середине звеньев
, расположены на середине звеньев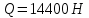 .
.