Лекция 9
 Скачать 426.5 Kb.
|
Силовой расчет Краткое содержание: Силовой расчет. Исходные данные для силового расчета. Порядок силового расчета. Метод Жуковского. Силы инерции, действующие на звенья кривошипно-ползунного механизма. Пример выполнения ДЗ№2.  Силовой расчет рычажных механизмов Во время движения механизма в его кинематических парах действуют силы, являющиеся силами взаимодействия между звеньями. Напомним, что эти силы относятся к категории внутренних по отношению к механизму в целом. Нагруженность кинематических пар силами взаимодействия является важной динамической характеристикой механизма. Знание сил в кинематических парах необходимо для расчета звеньев механизма на прочность, жесткость, вибростойкость, износоустойчивость, для расчетов подшипников на долговечность и для проведения других подобных расчетов, выполняемых при проектировании механизма. Определение внутренних сил, а также — в целом ряде задач — сил и пар сил, приложенных к механизму извне, составляет содержание его силового расчета. Изложение методов силового расчета будет сделано только для плоских механизмов. При этом примем, что механизм имеет плоскость симметрии, которая параллельна плоскости движения и в которой действуют все приложенные силы. Указанному условию отвечает очень большое число механизмов энергетических, технологических, транспортных машин и различных приборов. Силовой расчет следует выполнять с учетом ускоренного движения звеньев, так как их ускорения в современных быстроходных машинах весьма значительны. Неучет ускоренного движения звеньев вызовет недооценку нагружающих сил, что может привести к ошибкам в дальнейших инженерных расчетах. Учет ускоренного движения звеньев выполним методом кинетостатики, условно приложив к каждому подвижному звену механизма главный вектор, и главный момент сил инерции. Тогда для каждого звена можно записать уравнения кинетостатики. Главный вектор, и главный момент сил инерции определяются по уравнениям:  эти уравнения предполагают, что главный вектор сил инерции приложен к центру масс и направлен в сторону противоположную соответствующему ускорению, а главный момент сил инерции направлен против углового ускорения и его удобнее разбивать на пару сил:  .Следует подчеркнуть, что никакой силы  ; и никакой пары сил  к звену в действительности не приложено. Главный вектор и главный момент сил инерции не имеют никакого физического содержания и в расчетных уравнениях играют роль не более чем чисто математических величин, посредством которых учитывается влияние ускоренного движения звеньев.Силы в кинематических парах, являющиеся искомыми, определяют из уравнений, в которых они содержатся в составе сумм. Поскольку значения сил инерции зависят от ускорений, искомые силы также зависят от ускорений. Следовательно, для проведения силового расчета надо знать закон движения механизма. Исходные данные для силового расчета
Силовой расчет позволяет определить
Порядок силового расчета
Принцип Д’Аламбера: При движении механической системы активные силы, силы реакций связей вместе с силами инерции образуют равновесную систему сил для каждой точки системы. Таким образом, в конкретный момент времени можно к рассматриваемой системе применять уравнения статики:  При этом, если все моменты разложены на пары сил, а расчетные схемы построены в одном масштабе, то плечи для определения моментов берутся с чертежа в мм, а за положительное направление поворота принимают направление против часовой стрелки. Для нахождения сумм сил строятся планы сил в определенном масштабе, который может быть различным для различных расчетных схем. Существует ряд правил, позволяющих упростить решение поставленной задачи:
Для каждой расчетной схемы может быть решена задача с тремя неизвестными. Если в предложенной расчетной схеме две неизвестных величины (величина и направление одной силы; величины двух сил, при этом их направления известны), то результат можно получить, используя план сил. Если в предложенной расчетной схеме три неизвестных (и при этом возможно составить уравнение моментов!) то:
Метод Жуковского Для применения этого метода необходимо повернуть план скоростей на  (рекомендуется поворачивать в сторону противоположную  ). Переносим все заданные силы, действующие в рассматриваемый момент времени на звенья механизма, в том числе и силы инерции, в одноименные точки повернутого плана скоростей, не изменяя при этом величины и направления этих сил. (Силы реакции в Рычаге Жуковского не участвуют!) Составляем уравнение моментов всех перенесенных сил относительно полюса плана скоростей, т. е. рассматриваем план скоростей как некоторый рычаг с опорой в полюсе плана скоростей, находящийся под действием всех рассматриваемых сил в равновесии. Плечи всех сил берутся непосредственно с чертежа в мм. Подобная геометрическая интерпретация принципа возможных перемещений представляет значительные удобства для решения многих задач динамики механизмов. Метод этот получил название метода Жуковского по имени ученого, которым он был предложен, а рычаг, которым пользуются в этом методе, назван рычагом Жуковского. Метод Жуковского может быть применен для нахождения величины какой-либо одной неизвестной силы из числа сил, входящих в уравнение моментов, если точка приложения и направление этой силы заданы, а также заданы величины, направления и точки приложения всех остальных сил. В самом деле, в этом случае в записанном уравнении будет только одна неизвестная величина искомой силы, которая из него и определится. Силы инерции, действующие на звенья кривошипно-ползунного механизма 1 Построение плана механизма в масштабе.  2. Кинематическое исследование механизма Построение плана скоростей.
Построение плана ускорений.
3 Определение сил инерции. Звено 1:  , т.к.  ;  .Звено 2:  ,  .Звено 3:  ,  , т.к.  .Знак «минус» показывает, что силы инерции направлены противоположно ускорениям центров масс, а моменты сил инерции направлены противоположно угловым ускорениям. |
;
;
;
; 
; 
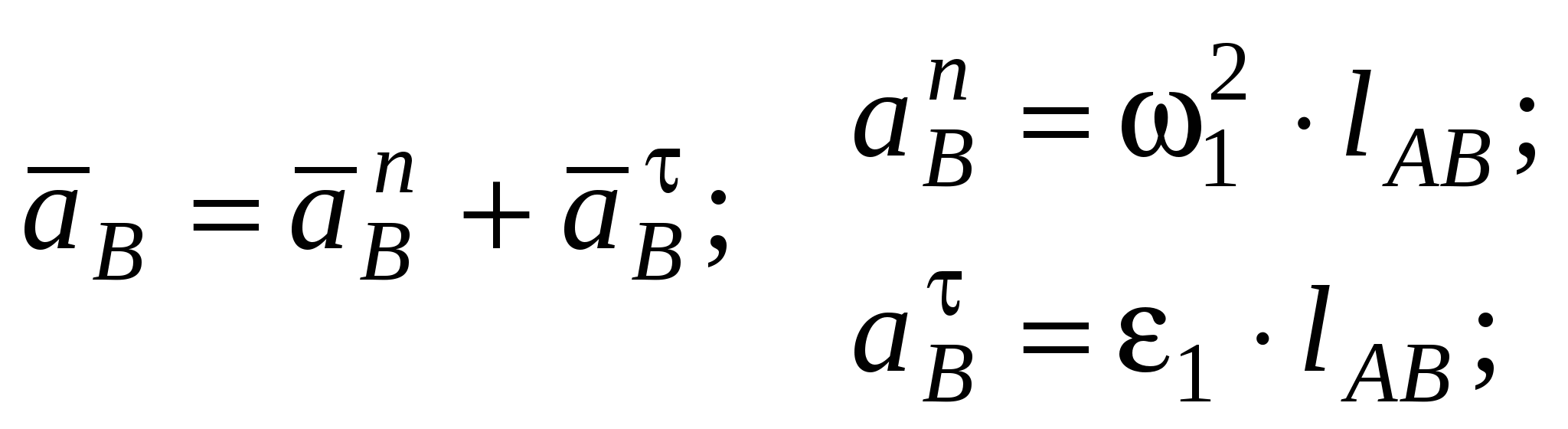