МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ (1). Квадратурные формулы прямоугольников, трапеций и Симпсона с переменным шагом. Оценка погрешности
 Скачать 1.09 Mb. Скачать 1.09 Mb.
|
|
Министерство высшего образования и науки Российской Федерации ФГБОУ ВО «ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «Прикладной математики и информатики» КУРСОВАЯ РАБОТА по дисциплине «Методы вычислений» на тему «Квадратурные формулы прямоугольников, трапеций и Симпсона с переменным шагом. Оценка погрешности». Вариант №5 Выполнила: Студентка3-го курса гр. М831 Алиева А.А. . Приняла: Ст. преп.кафедры «ПМиИ» Алиосманова О.А. Каспийск 2020 г Министерство высшего образования и науки РФ ФГБОУ ВО «ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Филиал в г.Каспийске Кафедра «Прикладной информатики и математики» Для направления «Программная инженерия» Задание на курсовую работу (проект) Студентки 3 курса М831 группы Алиевой А.А. По дисциплине «Методы вычисления»
Руководитель курсовой работы (проекта)(Алиосманова О.А.) Задание принял к исполнению (Алиева А.А.) Аннотация В данной работе рассмотрены решение квадратурных формул прямоугольников, трапеций и Симпсона с переменным шагом, оценка погрешности. В рамках курсовой работы решения реализованы на языке блок-схем алгоритма и программ на языке программирования С++. Кроме этого, наши вычисления производятся в среде: Excel и расписаны вручную. Курсовая содержит: рисунков –4 таблиц – 1 блок-схем - 3 страниц машинописного текста – 27 библиографические источники – 5 СОДЕРЖАНИЕ Введение……………………………………………………………...5 Метод прямоугольников..................................................................7 Метод трапеций................................................................................8 Метод Симпсона ( метод парабол) ................................................9 Задание по курсовой работе ...........................................................12 Ручной расчёт.........................................................................................13 Метод трапеций..............................................................................13 Блок-схемы программ...........................................................................16 Блок-схема метод прямоугольника.................................................16 Блок-схема метод трапеций ............................................................17 Блок-схема метод Симпсона............................................................19 Результаты полученные на ЭВМ......................................................21 Заключение............................................................................................23 Литература............................................................................................24 Приложение..........................................................................................25 Введение Одной из распространённых задач по численным методам, является – приближенное вычисление определенных интегралов. В этой курсовой мы рассмотрим три метода приближенного вычисления определённого интеграла – метод трапеций , метод Симпсона и метод прямоугольников. Что бы вычислить интеграл можно найти первообразную функцию и использовать формулу Ньютона-Лейбница, вычислив точное значение определённого интеграла. Но формула Ньютона-Лейбница 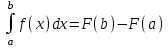 имеет ограниченное применение: имеет ограниченное применение:
Рассмотрим демонстрационный пример с рисунком. Вычислить определённый интеграл 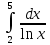 Всё было бы хорошо, но в данном примере интеграл не берётся – перед вами не берущийся, так называемый интегральный логарифм. А существует ли вообще этот интеграл? Изобразим на чертеже график подынтегральной функции f(x) = 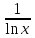 : : 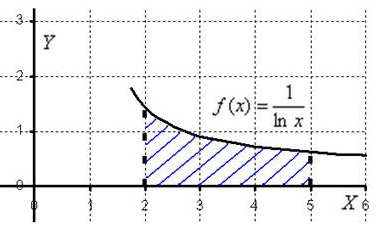  Всё нормально. Подынтегральная функция непрерывна на отрезке [2;5] и определённый интеграл 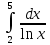 численно равен заштрихованной площади. Да вот только одна загвоздка – интеграл не берётся. И в подобных случаях на помощь как раз приходят численные методы. численно равен заштрихованной площади. Да вот только одна загвоздка – интеграл не берётся. И в подобных случаях на помощь как раз приходят численные методы. При этом задача встречается в двух формулировках: 1) Вычислить определённый интеграл приближённо, округляя результат до определённого знака после запятой. Например, до двух знаков после запятой, до трёх знаков после запятой и т.д. Предположим, получился приближенный ответ 5,347. На самом деле он может быть не совсем верным (в действительности, скажем, более точный ответ 5,343). Наша задача состоит лишь в том, чтобы округлить результат до трёх знаков после запятой. 2) Вычислить определённый интеграл приближённо, с определённой точностью. Например, вычислить определённый интеграл приближённо с точностью до 0,001. Что это значит? Это значит, что если получен приближенный ответ 5,347, то все цифры должны быть железобетонно правильными. А точнее говоря, ответ 5,347 должен отличаться от истины по модулю (в ту или другую сторону) не более чем на 0,001. Численные методы интегрирования универсальны: позволяют вычислить значение определённого интеграла непосредственно по значениям подынтегральной функции f(x), независимо от способа её задания или вида аналитического выражения. Геометрический смысл определённого интеграла – площадь криволинейной трапеции, ограниченной осью OX, кривой f(x), и прямыми x=a и x=b (Рис 2). Численные методы интегрирования основаны на различных способах оценки этой площади, поэтому полученные формулы численного интегрирования называются квадратурными (формулами вычисления площади). Существуют несколько основных методов приближенного вычисления определённого интеграла, который встречается в задачах: Метод прямоугольников. Д 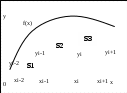 ля нахождения значения определённого интеграла ля нахождения значения определённого интеграла 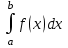 , разобьём отрезок [a, b] на n частей с шагом , разобьём отрезок [a, b] на n частей с шагом 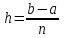 . Заменим на каждом частичном отрезке криволинейную фигуру прямоугольником. . Заменим на каждом частичном отрезке криволинейную фигуру прямоугольником.Одна сторона прямоугольника равна шагу разбиения, а в зависимости от того, какой будет вторая сторона, формула прямоугольников меняет свой вид и название:
Значение функции в точке xn не берётся, т.к. по данному значению прямоугольник уже не строится (выходим за пределы отрезка [a, b]).
Погрешность метода возникает по тем же причинам, что и в методе трапеций. Наименьшую погрешность имеет формула средних прямоугольников. Чтобы получить более точное значение интеграла, необходимо увеличить число разбиений. Метод трапеций. Идея аналогична. Отрезок интегрирования разбивается на несколько промежуточных отрезков, и график подынтегральной функции приближается ломаной линией: 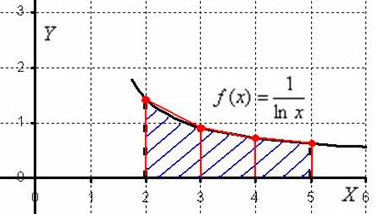 Таким образом, наша площадь (синяя штриховка) приближается суммой площадей трапеций (красный цвет). Отсюда и название метода. Легко заметить, что метод трапеций даёт значительно лучшее приближение, чем метод прямоугольников (при одинаковом количестве отрезков разбиения). И, естественно, чем больше более мелких промежуточных отрезков мы рассмотрим, тем будет выше точность. Рассмотрим определённый интеграл I= 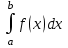 , где f(x) – функция, непрерывная на отрезке[a;b] . , где f(x) – функция, непрерывная на отрезке[a;b] . Проведём разбиение отрезка [a;b] на n равных отрезков:[x0;x1],[x1;x2],[x2,x3], [xn-1;xn]. При этом, очевидно: x0=a (нижний предел интегрирования) и xn=b (верхний предел интегрирования). Точки x0, x1, x2, x3, … xn-1, xn также называют узлами. Тогда определённый интеграл можно вычислить приближённо по формуле трапеций: 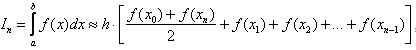 1.2 1.2h= 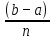 – длина каждого из маленьких отрезков или шаг; – длина каждого из маленьких отрезков или шаг;f(xi) – значения подынтегральной функции в точках x0, x1, x2, x3, … xn-1, xn. Метод Симпсона (метод парабол). Это более совершенный способ – график подынтегральной функции приближается не ломаной линией, а маленькими параболами. Сколько промежуточных отрезков – столько и маленьких парабол. Если взять те же три отрезка, то метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод трапеций. Чертёж строить не вижу смысла, поскольку визуально приближение будет накладываться на график функции f(x)= 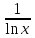 (ломаная линия предыдущего пункта – и то практически совпала). (ломаная линия предыдущего пункта – и то практически совпала).Задача на вычисление определённого интеграла по формуле Симпсона – самое популярное задание на практике. И методу парабол будет уделено значительное внимание. Рассмотрим определённый интеграл I= 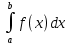 , где f(x) – функция, непрерывная на отрезке[a;b] . , где f(x) – функция, непрерывная на отрезке[a;b] . Проведём разбиение отрезка [a;b] на чётное количество равных отрезков. Чётное количество отрезков обозначают через 2n. На практике отрезков может быть: два: 2n=2  четыре:2n=4  восемь: 2n=8  десять:2n=10  двадцать: 2n=20 Число 2n понимается как единое число . То есть, нельзя сокращать, например, 2b=4 на два, получая n=4. Запись 2n лишь обозначает, что количество отрезков чётно. И ни о каких сокращениях речи не идёт. Итак, наше разбиение имеет следующий вид: [a=x0;x1],[x1;x2],[x2;x3];…, [x2n-2;x2n-1],[x2n-1; x2n=b] Термины аналогичны терминам метода трапеций: Точки x0, x1, x2, x3, … x2n-2, x2n-1,xn называют узлами. Формула Симпсона для приближенного вычисления определённого интеграла имеет следующий вид: 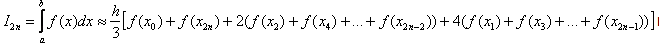 где: h= 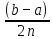 – длина каждого из маленьких отрезков или шаг; – длина каждого из маленьких отрезков или шаг;f(x) – значения подынтегральной функции в точках  . .Детализируя это нагромождение, разберу формулу подробнее: f(x0) + f(x2n) – сумма первого и последнего значения подынтегральной функции; 2(f(x2)+ f(x4)+…+ f(x2n-2) ) – сумма членов с чётными индексами умножается на 2; 4(f(x1) +f(x3)+. . .+ f(x2n-1) ) – сумма членов с нечётными индексами умножается на 4. Задание Вариант №5 Квадратурные формулы прямоугольников, трапеций Симпсона с переменным шагом. Оценка погрешности.
Пример 1. Дана табличная функция:
Пример 2. Дан интеграл: Y= 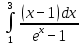 Блок схема Метод прямоугольников начало  Ввод y  Вызов функции integram  Вывод y  Конец Функция integram Ввод h, S, x, i  H=(b-a)*0,1/n S=0    I=0,n-1  X=x+i*h S=S+f(x)  S=h*s Retyrn y Функция y F=(x-1)/(exp(x)-1) Блок-схема Метод трапеций double f(double x) (x-1)/(exp(x)-1 double I(double a, double b, int n, double y (-3xx+2x+9) (b-a)/(2n)y int main() int n double a, b, y, dy, In cin a b n n>1 True dy=(b-a)/n y+=f(a)+f(b) False int I=1  i Y+=2(ƒ(a+dy*i)) i++  In= I(a, b, n,y) cout in  False True else cout “Wrong data” Блок схема Метод Симпсона double f(double x) (x-1)/(exp(x)-1) Sin(xx+2x) int main() double a, b, eps cin a b eps Double I=eps+1, I1=0 int N=2  (N<=4)||(fabs(I1-I)>eps) True False double h, sum2=0, sum4=0, sum=0 cout h=(b-a)/(2*N) I1 End I 0 int i=1 i<=2*N-1 sum4+=f(a+h*i) sum2+=f(a+h*(i+1)) i+=2  sum=f(a)+4*sum4+2*sum2-f(b) I=I1 I1=(h/3)*sum N*=2  Результаты полученные на ЭВМ используя табличный процессор Excel.Метод прямоугольников 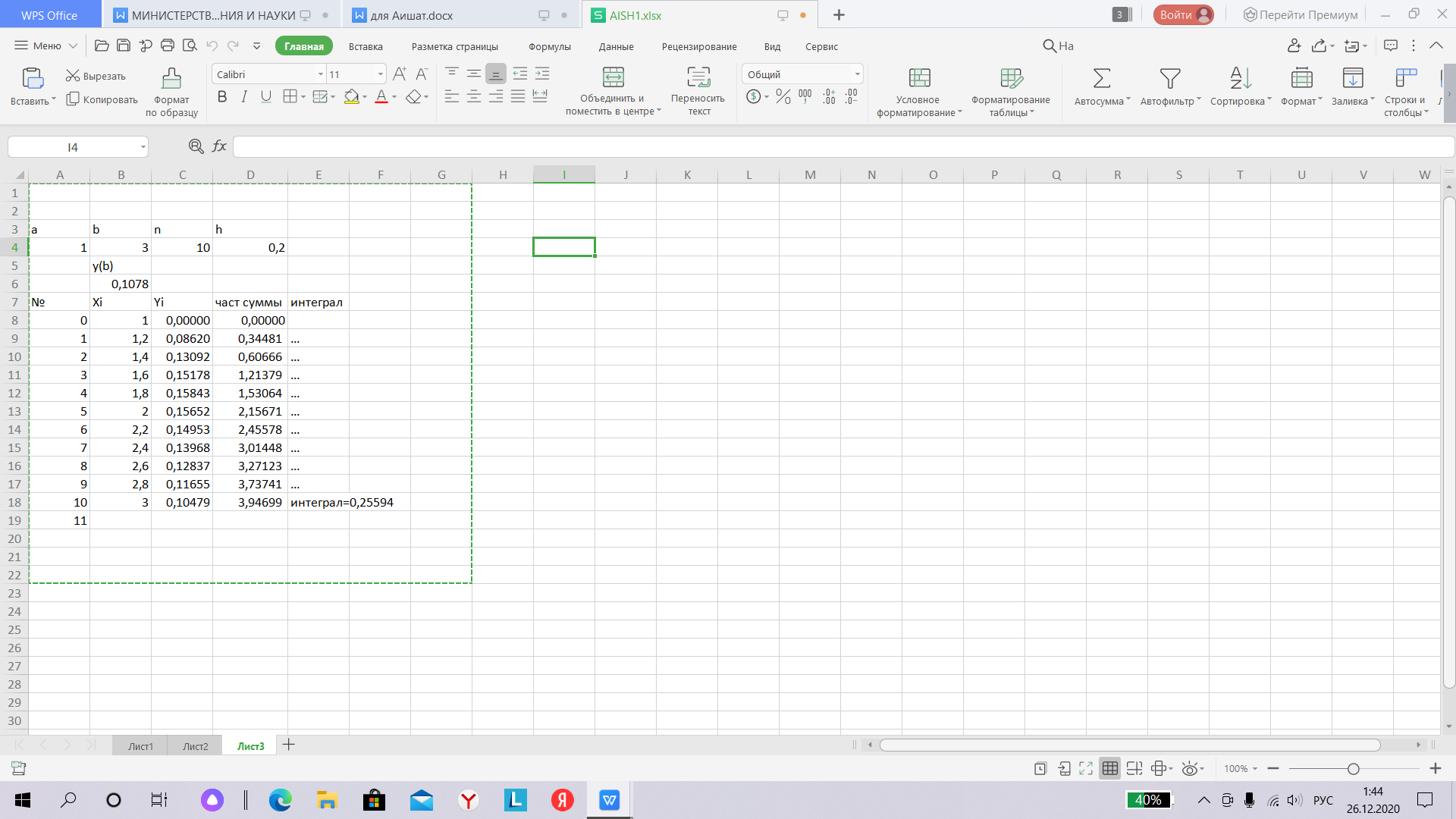 Метод трапеций 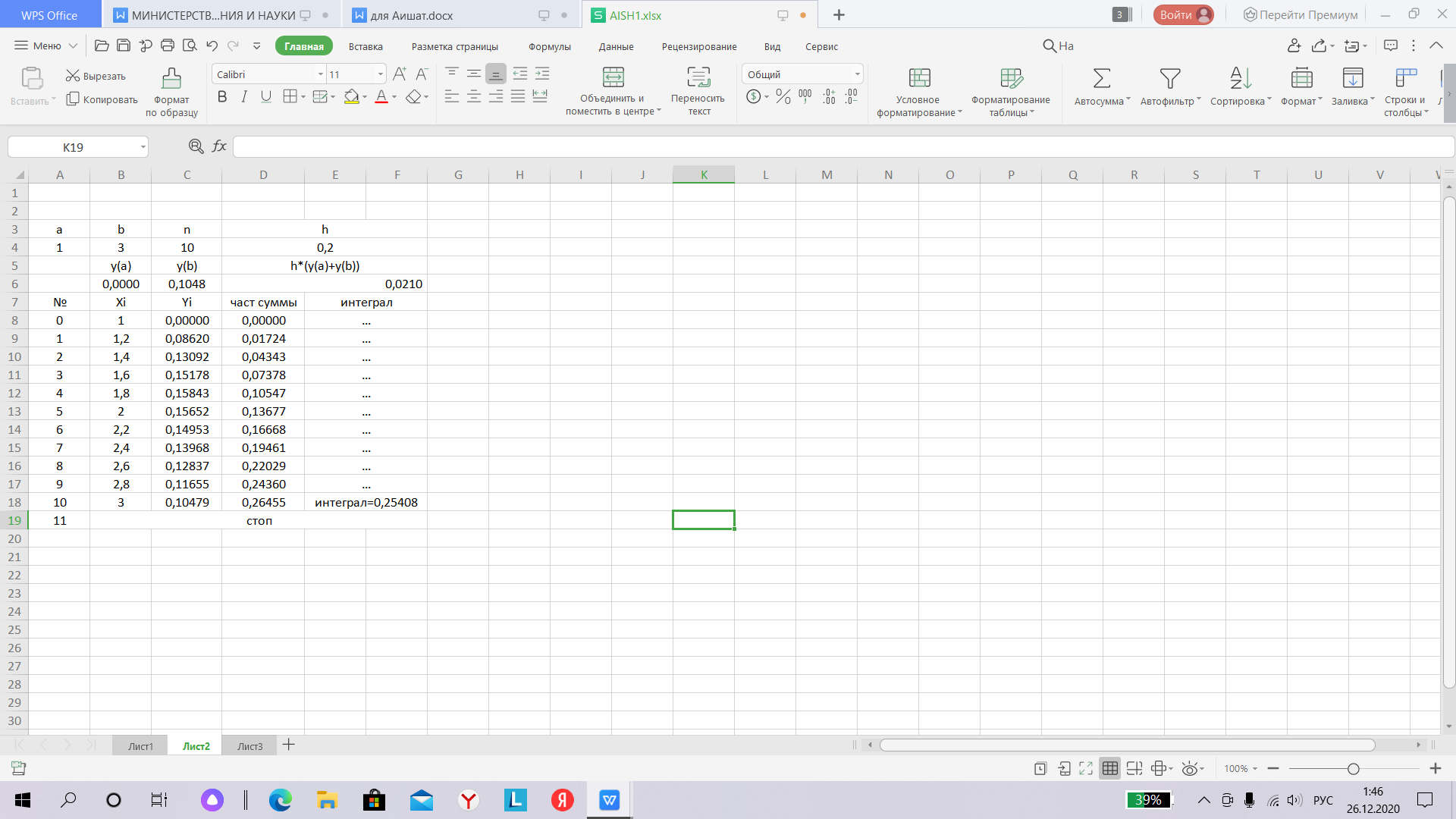 Метод Симпсона 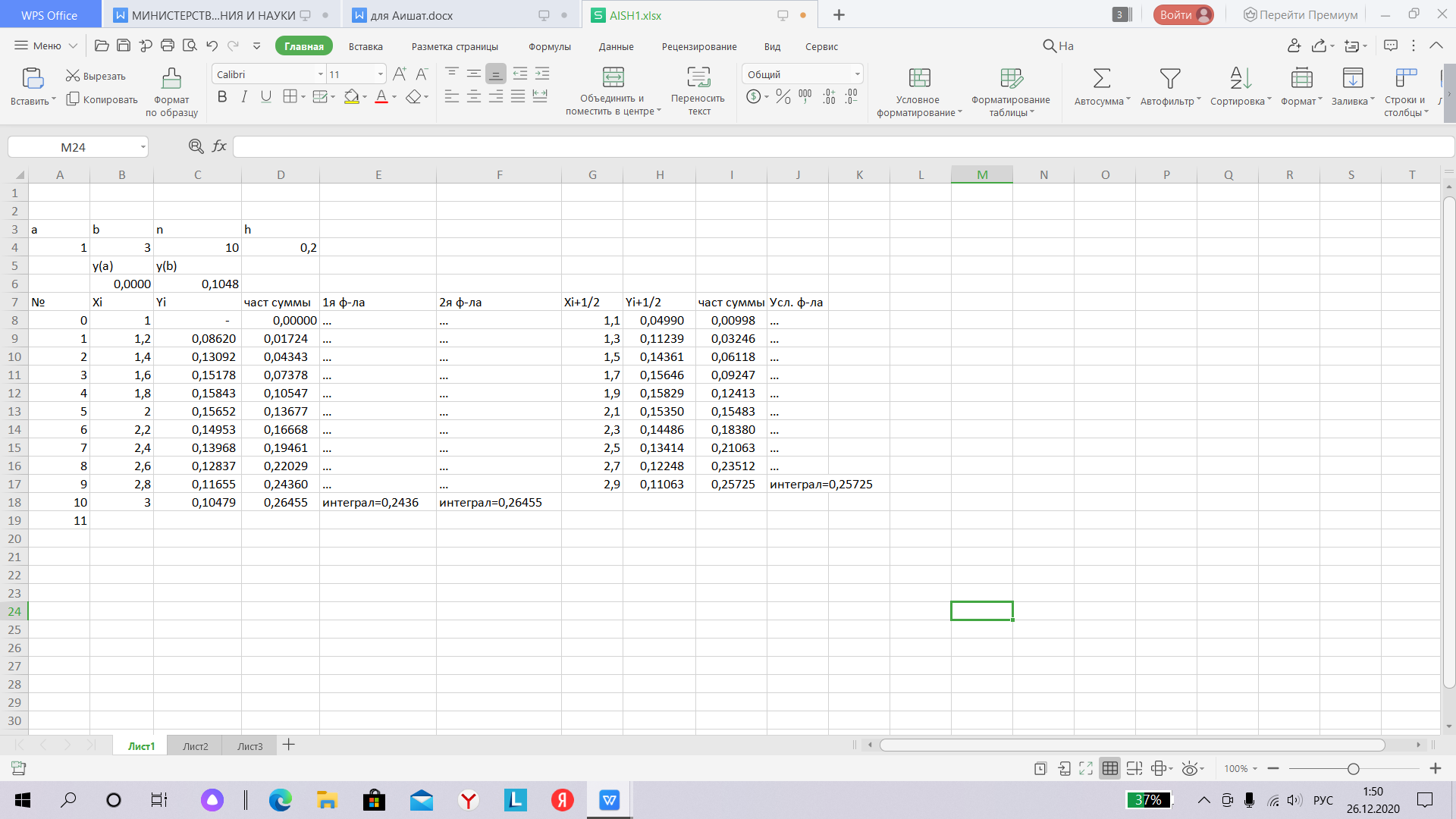 Заключение Таким образом очевидно, что при вычислении определенных интегралов методами трапеций и средних прямоугольников не даёт нам точного значения, а только приближенное. Чем ниже задаётся численное значение точности вычислений (основание трапеции или прямоугольника, в зависимости от метода), тем точнее результат получаемый машиной. При этом, число итераций составляет обратно пропорциональное от численного значения точности. Следовательно для большей точности необходимо большее число итераций, что обуславливает возрастание затрат времени вычисления интеграла на компьютере обратно пропорционально точности вычисления. Использование для вычисления одновременно двух методов (трапеций и средних прямоугольников) позволило исследовать зависимость точности вычислений при применении обоих методов. Следовательно при понижении численного значения точности вычислений результаты расчётов по обеим методам стремятся друг к другу и оба к точному результату. Список используемой литературы
Приложение Метод прямоугольников #include #include #include using namespace std; float f(float x) { Return((x-1)/(exp(x)-1)); } float integralpram(int a,int b,int n) { float h,S,x; int i; h=(b-a) * 1.0 /n; S=0; for(i=0;i { x=a+i*h; S=S+f(x); } S=h*S; return S; } int main() { float y; y=integralpram(1,3,10); cout< }  Метод трапеций #include #include using namespace std; double f(double x) {return ((x-1)/(exp(x)-1); } double I(double a,double b,int n,double y) {return ((b-a)/(2*n)*y); } int main() { int n; double a,b,y,dy,In; cin>>a>>b>>n; if (n>1) { dy=(b-a)/n; y+=f(a)+f(b); for (int i=1; i { y+=2*(f(a+dy*i)); } In=I(a,b,n,y); cout << In; } else {cout <<"Wrong data";} }  Метод Симпсона #include #include using namespace std; double f(double x) { return sin((x-1)/(exp(x)-1)); } Int main() { double a, b, eps; cin>>a>>b>>eps; double I=eps+1, I1=0; for (int N=2; (N<=4)||(fabs(I1-I)>eps); N*=2) { double h, sum2=0, sum4=0, sum=0; h=(b-a)/(2*N);. for (int i=1; i<=2*N-1; i+=2) { sum4+=f(a+h*i);. sum2+=f(a+h*(i+1)); } sum=f(a)+4*sum4+2*sum2-f(b);. I=I1; I1=(h/3)*sum; } cout << I1 << endl; return 0;}  |

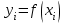 формула приобретает вид:
формула приобретает вид: