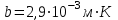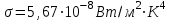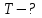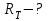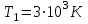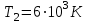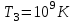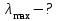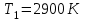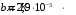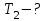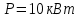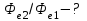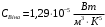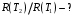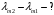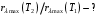физикаа. Квантова природа випромінювання розділ vii квантова природа випромінювання приклади розвязування задач
 Скачать 427.48 Kb. Скачать 427.48 Kb.
|
|
7.8. Визначити температуру і енергетичну світність абсолютно чорного тіла, якщо максимум енергії випромінювання припадає на довжину хвилі 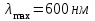 . .
Згідно з першим законом Віна 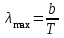 , таким чином температура абсолютно чорного тіла , таким чином температура абсолютно чорного тіла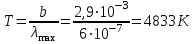 . .За законом Стефана-Больцмана інтегральна випромінювальна здатність: 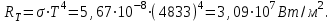 7.9. В яких ділянках спектра знаходяться довжини хвиль, що відповідають максимуму спектральної густини енергетичної світності, якщо джерелами світла є: 1. спіраль електричної лампи ( 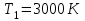 ); 2. поверхня сонця ( ); 2. поверхня сонця (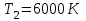 ); 3. атомна бомба, в момент вибуху якої температура становить ); 3. атомна бомба, в момент вибуху якої температура становить 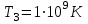 ? Випромінювання вважати близьким до випромінювання абсолютно чорного тіла ? Випромінювання вважати близьким до випромінювання абсолютно чорного тіла
Згідно закону зміщення Віна: 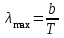 , ,тому довжини хвиль, що відповідають зазначеним в умові задачі температурам: 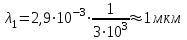 , , 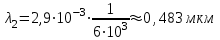 , , 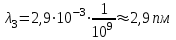 . .7.10. Абсолютно чорне тіло мало температуру 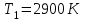 . Внаслідок остигання тіла довжина хвилі, на яку припадає максимум спектральної густини енергетичної світності, змінилась на . Внаслідок остигання тіла довжина хвилі, на яку припадає максимум спектральної густини енергетичної світності, змінилась на 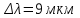 . До якої температури охололо тіло? . До якої температури охололо тіло?
Довжину хвилі, яка відповідає максимуму спектральної густини енергетичної світності, можна знайти із закону зміщення Віна: 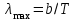 . Таким чином, . Таким чином, 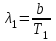 ; ; 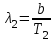 , , отже зміна довжини хвилі 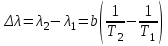 , , Звідси 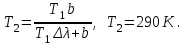 7.11. Потужність випромінювання абсолютно чорного тіла становить Р = 10 кВт. Визначити площу випромінювальної поверхні тіла, якщо відомо, що довжина хвилі, на яку припадає максимум спектральної густини його енергетичної світності, становить 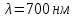 . .Розв’язування
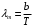 , , звідки 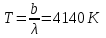 . .Енергетичну світність можна знайти із закону Стефана-Больцмана: 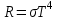 . . Потужність випромінювання абсолютно чорного тіла 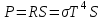 , , отже 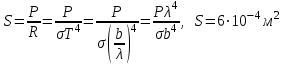 . .7.12. У скільки разів зміниться потік випромінювання абсолютно чорного тіла, якщо максимум енергії випромінювання зміститься з червоної межі видимого спектра ( 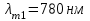 ) у фіолетову ( ) у фіолетову (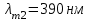 )? )?
Розв’язування Потік випромінювання 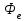 абсолютно чорного тіла пов'язаний з енергетичною світністю співвідношенням абсолютно чорного тіла пов'язаний з енергетичною світністю співвідношенням 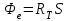 , ,де 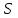 - площа випромінюючої поверхні. За законом Стефана-Больцмана - площа випромінюючої поверхні. За законом Стефана-Больцмана 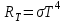 . .Абсолютну температуру можна знайти із закону зміщення Віна: 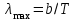 . . Остаточно формула для визначення потоку випромінювання абсолютно чорного тіла набуде вигляду: 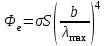 . .Таким чином, 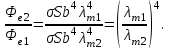 Знаходимо числове значення шуканої величини : 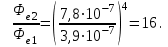 7.13. Температура абсолютно чорного тіла зросла від 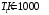 до до 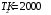 . У скільки разів зросла його енергетична світність? На скільки змінилася довжина хвилі, на яку припадає максимум спектральної густини енергетичної світності? У скільки разів зросла максимальна спектральна густина енергетичної світності тіла? . У скільки разів зросла його енергетична світність? На скільки змінилася довжина хвилі, на яку припадає максимум спектральної густини енергетичної світності? У скільки разів зросла максимальна спектральна густина енергетичної світності тіла? Розв’язування
Користуючись законом Стефана-Больцмана, маємо: 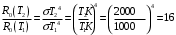 . .Зміну довжини хвилі, на яку припадає максимум спектральної густини енергетичної світності знайдемо за допомогою закону зміщення Віна: 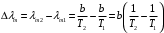 . .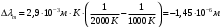 . .Згідно другого закону Віна, максимальне значення спектральної густини енергетичної світності абсолютно чорного тіла 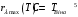 . .Отже, 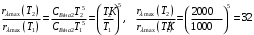 . .7.14. Температура абсолютно чорного тіла 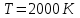 . Визначити довжину хвилі, на яку припадає максимум енергії випромінювання і спектральну густину енергетичної світності (випромінювальну здатність) для цієї довжини хвилі. . Визначити довжину хвилі, на яку припадає максимум енергії випромінювання і спектральну густину енергетичної світності (випромінювальну здатність) для цієї довжини хвилі.
Довжину хвилі, на яку припадає максимум енергії випромінювання, знайдемо за першим законом Віна: 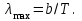 Максимальну випромінювальну здатність знайдемо за другим законом Віна: 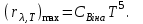 Знаходимо числові значення шуканої величини: 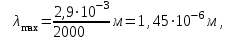 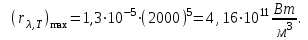 7.15. Визначити енергію, масу та імпульс фотона, якщо довжина хвилі дорівнює = 2,0 пм.
Для того, щоб визначити енергію фотона, скористаємось виразом: 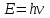 , (1) , (1)де h – стала Планка а – частота коливань. Оскільки в умові задачі задана довжина хвилі, то скористаємось наступним виразом, який виражає зв'язок між довжиною хвилі та частотою коливань: 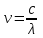 . (2) . (2)Підставивши вираз (2) в (1), отримаємо: 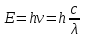 . . Використовуючи дані умови задачі, визначимо енергію кванта: 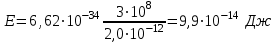 . . Масу фотона можна визначити з виразу: 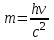 . . Використавши формулу (2), отримаємо: 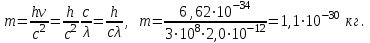 І насамкінець для розрахунку величини імпульсу фотона скористаємось виразом: 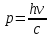 , , в якому частоту коливань визначимо за формулою (2): 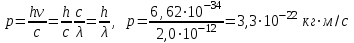 . . 7.16. Ртутна лампа має потужність Р = 125 Вт. Скільки фотонів світла випромінюється щосекунди для довжин хвиль: 1) 1 = 612,3 нм; 2) 2 = =579,1 нм? Інтенсивність цих ліній відповідно становить: 1) I1 =2 %; 2) I2= =4 % від інтенсивності випромінювання ртутної лампи. Врахувати, щоk = 80 % потужності витрачається на випромінювання.
Кількість фотонів ni, котра припадає на довжину хвилі j (в даній задачі j = 1, 2), можна розрахувати, розділивши сумарну енергію всіх фотонів Ej, яка випромінюється для даної довжини хвилі j, на енергію одного фотона: 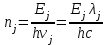 , (1) , (1)де h – стала Планка. У виразі (1) використано зв'язок між частотою коливань та їх довжиною хвилі : 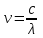 , (2) , (2)де c – швидкість світла. В свою чергу, сумарна енергія всіх фотонів Ej, яка випромінюється для даної довжини хвилі j, це не що інше, як інтенсивність даної спектральної лінії: 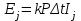 , (3) , (3)де коефіцієнт k вказує на те, що лише k = 80% потужності ртутної лампи витрачається на випромінювання. Також в (3) слід врахувати , що відрізок часу, який розглядається, становить t = 1 с, тому надалі множник t будемо опускати. Підставивши (3) в (1), отримаємо робочу формулу: 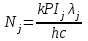 . (4) . (4)За допомогою рівняння (4) розрахуємо кількість фотонів, які випромінюються для 1 = 612,3 нм - 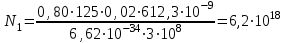 , ,для 2 = 579,1 нм - 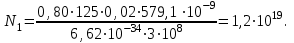 |