физикаа. Квантова природа випромінювання розділ vii квантова природа випромінювання приклади розвязування задач
 Скачать 427.48 Kb. Скачать 427.48 Kb.
|
|
7.17. Червона межа фотоефекту для деякого металу дорівнює ч = 300 нм. Визначити: 1) роботу виходу електрона з металу; 2) максимальну швидкість електронів, які вириваються з металу світлом з довжиною хвилі = 150 нм; 3) максимальну кінетичну енергію електронів.
Основною формулою, яка використовується в розв’язанні задач про фотоефект, є закон збереження енергії для зовнішнього фотоефекту або формула Ейнштейна: 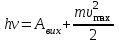 , (1) , (1)де 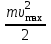 – це кінетична енергія електрона, вирваного із металу . За означенням, для червоної межі зовнішнього фотоефекту вираз (1) набуває вигляду: – це кінетична енергія електрона, вирваного із металу . За означенням, для червоної межі зовнішнього фотоефекту вираз (1) набуває вигляду: 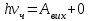 (2) (2)або, враховуючи зв'язок між частотою коливань та їх довжиною хвилі : 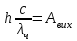 . (3) . (3)Підставивши дані умови задачі в (3), розрахуємо роботу виходу: 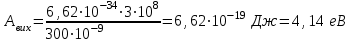 . Максимальну швидкість електронів, вирваних із металу випромінюванням із довжиною хвилі , можна визначити з (1) та (3) як: . Максимальну швидкість електронів, вирваних із металу випромінюванням із довжиною хвилі , можна визначити з (1) та (3) як: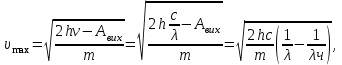 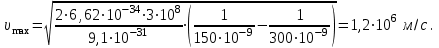 Для визначення максимальної кінетичної енергії скористаємось виразами (1) та (3): 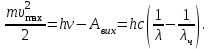 Підставимо числові значення: 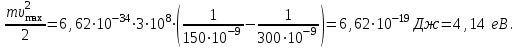 7.18. Для припинення фотоефекту, що викликаний опроміненням поверхні вольфраму ультрафіолетовим світлом, необхідно прикласти затримуючу різницю потенціалів у UW = 3,5 В.Якщо вольфрамову пластину замінити пластинкою з іншого металу, то затримуюча різниця потенціалів зменшиться до UХ = 3,3 В. Визначити роботу виходу електронів з поверхні іншого металу. що це за метал ?
Роботу виходу електронів з металу можна визначити за допомогою формули Ейнштейна: 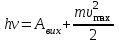 . . В довідкових таблицях знайдемо роботу виходу для вольфраму Авих W= 4,5 еВ. За означенням затримуючої різниці потенціалів, на її подолання фотоелектрону необхідно витратити всю свою кінетичну енергію. Або, інакше кажучи, потенціальна енергія затримуючого електричного поля по модулю дорівнює кінетичній енергії фотоелектрона: 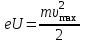 . . Використовуючи ці дані, можемо знайти енергію квантів ультрафіолетового світла: 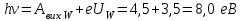 . . Тоді робота виходу невідомого металу становить: 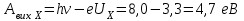 . . Згідно із довідниковими даними робота виходу 4,7 еВ відповідає сріблу. 7.19. Кванти світла з енергією h = 5,0 еВвиривають фотоелектрони з металу, який має роботу виходу А = 4,7 еВ.Визначити максимальний імпульс, який отримує поверхня металу при вильоті одного електрона.
Максимальний імпульс, отриманий поверхнею внаслідок виривання електрона можна визначити із закону збереження імпульсу для системи, яка складається з електрона та поверхні. Відповідні імпульси позначимо як Рe та Рпов, а індексами 1 та 2 – стани системи до і після поглинання фотона, відповідно. Тоді закон збереження імпульсу матиме вигляд: 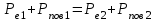 . (1) . (1)Якщо врахувати. що до взаємодії з фотоном як електрон, так поверхня були нерухомими, тобто Рe1 = Рпов1 = 0, то (1) набере вигляду: 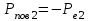 . (2) . (2)Отже, для розв’язання задачі необхідно визначити імпульс фотоелектрона (вирваного електрона). Для цього скористаємось основним виразом, який описує зовнішній фотоефект, а саме формулою Ейнштейна: 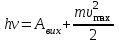 , (3) , (3)з якої можна визначити максимальну кінетичну енергію електрона емісії. Скористаємось зв’язком між кінетичною енергією та імпульсом тіла: 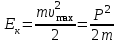 . (4) . (4)В даному випадку імпульс тіла Р з (4) відповідає імпульсу вирваного електрона Рe2. Підставивши (4) в (3) та врахувавши (2), отримаємо: 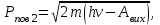 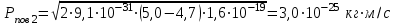 . .7.20. На дзеркальце з ідеальною відбиваючою поверхнею площею S = 1,0 см2 нормально падає світло. Визначити імпульс, отриманий дзеркальцем, якщо поверхнева густина потоку випромінювання, що падає на дзеркальце, становить w = 0,25 МВт/м2. Час опромінення 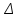 t = 2с. t = 2с.
Імпульс, отриманий будь-яким тілом, тобто приріст імпульсу цього тіла визначається за формулою: 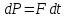 , (1) , (1)де dP – нескінченно малий приріст імпульсу, F – механічна сила, дія якої викликала зміну імпульсу dP, а dt – це час, протягом якого діяла сила. Якщо сила залишається незмінною в часі, то від приростів у (1) можемо перейти до скінчених змін фізичних величин: 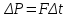 . (2) . (2)В даному випадку сила, що діє на дзеркальце, є наслідком тиску з боку потоку фотонів. Знаючи тиск p, що діє на поверхню S, можна визначити силу F, яка є причиною дії тиску: 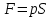 . (3) . (3)Відомо, що тиск світла на поверхню тіла становить: 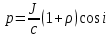 , (4) , (4)де 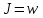 – енергія всіх фотонів, що падають на одиницю поверхні за одиницю часу, тобто поверхнева густина потоку випромінювання; – енергія всіх фотонів, що падають на одиницю поверхні за одиницю часу, тобто поверхнева густина потоку випромінювання; 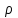 – коефіцієнт відбивання світла; – коефіцієнт відбивання світла; 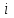 – кут падіння світла на поверхню. Підставивши (4) в (3) і в (2) та скориставшись даними умови задачі, отримаємо значення імпульсу, переданого електронами дзеркальцю протягом 2 секунд: – кут падіння світла на поверхню. Підставивши (4) в (3) і в (2) та скориставшись даними умови задачі, отримаємо значення імпульсу, переданого електронами дзеркальцю протягом 2 секунд: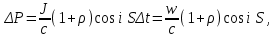 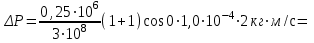 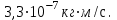 7.21. Світло з довжиною хвилі = 500нм, падаючи нормально на поверхню, створює тиск на неї p = 25·10-6н/м2. Яка кількість квантів падає щосекунди на одиницю площі цієї поверхні? Коефіцієнт відбивання світла = 0,5.
Тиск світла на поверхню тіла дорівнює: 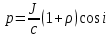 , (1) , (1)деJ – енергія всіх фотонів, що падають на одиницю поверхні за одиницю часу; – коефіцієнт відбивання світла; i – кут падіння світла на поверхню. Єдиною величиною в (1), яка характеризує інтенсивність потоку фотонів, а отже, дозволяє визначити їх кількість, є J: 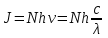 . (2) . (2)Підставивши (2) в (1), отримаємо: 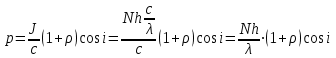 (3) (3)Звідки кількість фотонів: 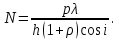 Знаходимо числове значення шуканої величини : 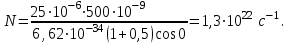 7.22. Рентгенівське випромінювання з довжиною хвилі = 25,0пм розсіюється на графіті. Визначити довжину хвилі, що розсіялась під кутом = 30º до напрямку падаючого променя.
Проходження випромінювання через легкі елементи, одним із яких є графіт, супроводжується комптонівським розсіянням квантів цього випромінюванням на електронах речовини. Експериментально це проявляється як зростання довжини хвилі розсіяного випромінювання: 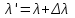 . . Зміну довжини хвилі випромінювання при комптонівському розсіюванні можна визначити за формулою: 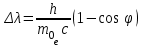 , , де 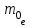 – маса спокою електрона, а – маса спокою електрона, а 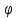 – кут розсіювання рентгенівських променів. Підставивши дані умови задачі, отримаємо: – кут розсіювання рентгенівських променів. Підставивши дані умови задачі, отримаємо: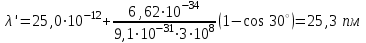 . . 7.23. Яка доля енергії фотона при ефекті Комптона припадає на електрон віддачі, якщо фотон був розсіяний на кут = 90º? Енергія фотона до розсіяння становила Еф = 0,5МеВ.
Приріст кінетичної енергії електрона відбувається за рахунок передачі йому частини енергії фотона падаючого випромінювання під час комптонівського розсіяння: 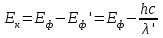 , (1) , (1)де Еф – це енергія фотона до розсіяння, а Е' та ' – енергія фотона та довжина хвилі після розсіяння, відповідно. Відомо, що зміна довжини хвилі під час комптонівського розсіяння становить 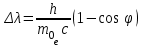 . (2) . (2)Тоді довжина хвилі ' розсіяного фотона: 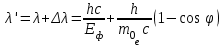 . (3) . (3)Підставивши (2) і (3) у вираз (1), отримаємо: 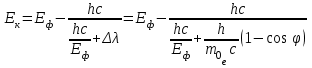 (4) (4)Використовуючи (1) та (4), можна розрахувати, яка частина енергії фотона була передана електрону віддачі: 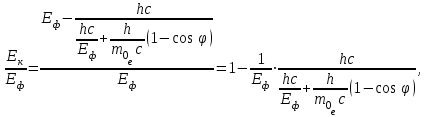 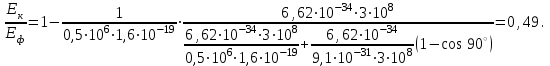 7.24. Рентгенівські промені з довжиною хвилі = 20пм здійснюють комптонівську взаємодію і розсіюються під кутом = 90°. Визначити: 1) зміну довжини хвилі рентгенівських променів при розсіюванні; 2) кінетичну енергію електрона віддачі; 3) імпульс електрона віддачі.
Зміну довжини хвилі рентгенівського випромінювання при комптонівському розсіюванні можна визначити за формулою: 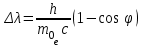 , (1) , (1)де 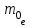 – маса спокою електрона, а – маса спокою електрона, а 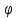 – кут розсіювання рентгенівських променів. Підставивши дані умови задачі, отримаємо: – кут розсіювання рентгенівських променів. Підставивши дані умови задачі, отримаємо: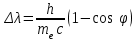 , (2) , (2)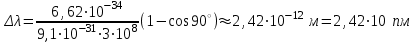 . .Відповідно, довжина хвилі рентгенівських променів, які зазнали комптонівського розсіяння під кутом = 90° становить: 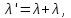 (3) (3)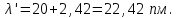 Під час комптонівського розсіяння збільшення кінетичної енергії електрона відбувається за рахунок зменшення енергії фотона, тобто: 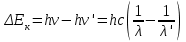 , (4) , (4)де та ' ( та ') – це частоти (довжини хвиль) фотона до і після розсіяння, відповідно. Оскільки згідно моделі комптонівського розсіяння електрон вважається нерухомим до моменту взаємодії із фотоном, то Eк = Eк. Зважаючи на це і підставивши в (4) числові значення з умови та результат (3), визначимо кінетичну енергію електрона розсіяння: 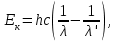 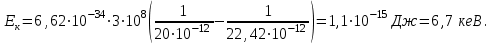 Скористаємось зв'язком між кінетичною енергією та імпульсом тіла: Скористаємось зв'язком між кінетичною енергією та імпульсом тіла: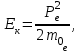 (5) (5)звідки: 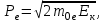 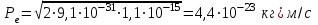 . . |

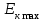 - ?
- ?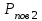 - ?
- ?
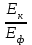 - ?
- ?