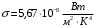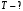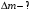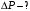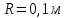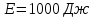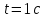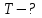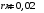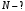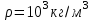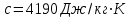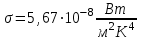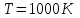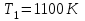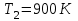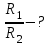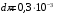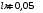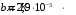физикаа. Квантова природа випромінювання розділ vii квантова природа випромінювання приклади розвязування задач
 Скачать 427.48 Kb. Скачать 427.48 Kb.
|
|
КВАНТОВА ПРИРОДА ВИПРОМІНЮВАННЯ РОЗДІЛ VII КВАНТОВА ПРИРОДА ВИПРОМІНЮВАННЯ Приклади розв’язування задач 7.1. Яка температура в печі, якщо відомо, що через оглядове віконце площею 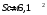 виходить пучок теплового випромінювання потужністю виходить пучок теплового випромінювання потужністю 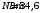 ? Випромінювання вважати близьким до випромінювання абсолютно чорного тіла. Знайти масу теплового випромінювання, що виходить через віконце за 1 секунду, та імпульс, який воно переносить за цей час. ? Випромінювання вважати близьким до випромінювання абсолютно чорного тіла. Знайти масу теплового випромінювання, що виходить через віконце за 1 секунду, та імпульс, який воно переносить за цей час.Розв’язування
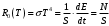 . .Звідси знаходимо температуру всередині печі:  , , , , 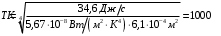 . . Обчислимо масу теплового випромінювання, яке виходить через віконце за одиницю часу. Враховуючи відому формулу для енергії кванта випромінювання 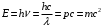 , ,і врахувавши, що загальна енергія, перенесена пучком випромінювання дорівнює сумі енергій окремих його квантів, маємо: 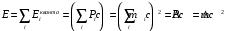 , , де 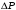 та та 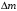 - імпульс та маса потоку теплового випромінювання, що переносить енергію - імпульс та маса потоку теплового випромінювання, що переносить енергію 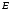 . Отже, за одну секунду пучок випромінювання перенесе через віконце масу та імпульс . Отже, за одну секунду пучок випромінювання перенесе через віконце масу та імпульс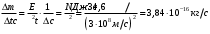 , , 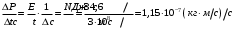 . . 7.2. Кулька, радіус якої R = 10 см, за постійної температури випромінює за секунду E = 1 кДж енергії. Визначити температуру кульки, якщо вважати її сірим тілом з коефіцієнтом чорноти 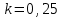 . .
Енергетична світність кульки згідно із законом Стефана-Больцмана 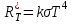 , з іншого боку. , з іншого боку. 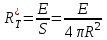 Прирівнюючи праві частини формул, можна легко знайти шукану температуру кульки: Прирівнюючи праві частини формул, можна легко знайти шукану температуру кульки: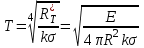 , , отже, 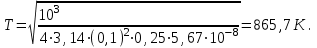 7.3. Яку потужність необхідно підводити до чорної металевої кульки радіусом  , щоби підтримувати її при температурі , щоби підтримувати її при температурі 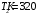 ? Температура оточуючого середовища ? Температура оточуючого середовища 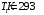 . Вважати, що обмін теплом відбувається лише через теплове випромінювання. . Вважати, що обмін теплом відбувається лише через теплове випромінювання.
Розв’язування Згідно закону Стефана-Больцмана, енергетична світність кульки 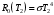 та оточуючого середовища: та оточуючого середовища: 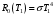 . Поверхня кульки площею . Поверхня кульки площею  є абсолютно чорною, а отже, випромінює потік теплового випромінювання потужністю є абсолютно чорною, а отже, випромінює потік теплового випромінювання потужністю 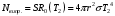 . . Разом із тим, вона поглинає все випромінювання оточуючого середовища, яке попадає на її поверхню, потужністю  . . Отже, для збереження вказаного температурного режиму, необхідно компенсувати втрати енергії кулькою через теплове випромінювання (кулька повинна випромінювати таку ж потужність, яку поглинає та отримує від нагрівника: 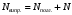 , , звідки 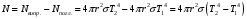 . . Знаходимо числове значення шуканої величини :  7.4. Яку потужність втрачає приміщення через 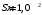 площі вікна внаслідок теплового випромінювання? В кімнаті температура площі вікна внаслідок теплового випромінювання? В кімнаті температура 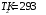 , надворі , надворі 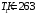 . Вважати, що приміщення та зовнішнє середовище випромінюють, як абсолютно чорні. . Вважати, що приміщення та зовнішнє середовище випромінюють, як абсолютно чорні. Розв’язування
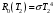 та оточуючого середовища: 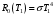 . . Теплове випромінювання з приміщення вважається таким, як в абсолютно чорного тіла, а отже, з приміщення випромінюється через площу вікна 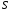 потік теплового випромінювання потужністю потік теплового випромінювання потужністю 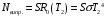 . . Разом з тим, з двору через вікно поступає теплове випромінювання оточуючого середовища, яке попадає на його поверхню 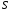 , потужністю , потужністю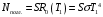 . . Отже, в сумі через поверхню вікна 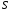 завдяки тепловому випромінюванню втрачається потік енергії потужністю: завдяки тепловому випромінюванню втрачається потік енергії потужністю: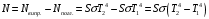 . .Знаходимо числове значення шуканої величини : 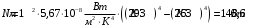 . .7.5. В чорну металеву посудину, що має форму куба, налито  води, температура якої води, температура якої 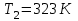 . Знайти час остигання посудини до температури . Знайти час остигання посудини до температури 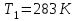 , якщо її помістили в чорний резервуар, температуру стінок якого можна прийняти такою, що дорівнює , якщо її помістили в чорний резервуар, температуру стінок якого можна прийняти такою, що дорівнює  . . Розв’язування
Кількість теплоти, що виділяється при остиганні води 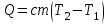 , ,де с – теплоємність води. Ця теплота виділяється за рахунок теплового випромінювання, тому  , ,причому 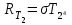 - енергія, що випромінюється - енергія, що випромінюється 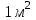 за за 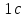 площі поверхні куба, площі поверхні куба, 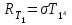 - енергія, що поглинається - енергія, що поглинається 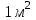 за за 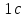 площі поверхні куба, площі поверхні куба, 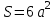 - площа поверхні куба, - площа поверхні куба, 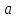 - сторона куба. Маса води в кубі - сторона куба. Маса води в кубі 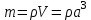 , де , де 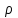 - густина води, тому сторона куба - густина води, тому сторона куба 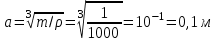 . .За законом збереження енергії 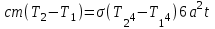 , ,звідки знаходимо час остигання посудини 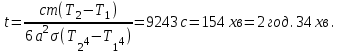 7.6. Поверхня нагріта до Т = 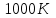 . Одну половину цієї поверхні нагрівають на Т1 = . Одну половину цієї поверхні нагрівають на Т1 = 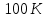 , а друга охолоджується на Т2 = , а друга охолоджується на Т2 = 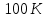 . В скільки разів зміниться енергетична світність поверхні цього тіла? . В скільки разів зміниться енергетична світність поверхні цього тіла?
Користуючись законом Стефана-Больцмана, запишемо для обох частин тіла – нагрітої: 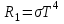 та охолодженої: та охолодженої: 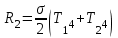 . Шукане відношення енергетичних світностей поверхні тіла можна розрахувати за формулою: . Шукане відношення енергетичних світностей поверхні тіла можна розрахувати за формулою: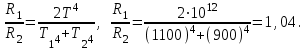 . .7.7. Діаметр вольфрамової спіралі в електричній лампі 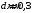 , її довжина , її довжина 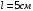 . При ввімкненні в електромережу з напругою . При ввімкненні в електромережу з напругою 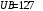 через спіраль тече струм силою через спіраль тече струм силою 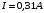 . Вважати, що при робочій температурі відношення енергетичної світності вольфраму та абсолютно чорного тіла . Вважати, що при робочій температурі відношення енергетичної світності вольфраму та абсолютно чорного тіла 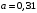 , та вся спожита лампою енергія витрачається на теплове випромінювання. Знайти температуру спіралі та довжину хвилі, якій відповідає максимум спектральної густини енергетичної світності. , та вся спожита лампою енергія витрачається на теплове випромінювання. Знайти температуру спіралі та довжину хвилі, якій відповідає максимум спектральної густини енергетичної світності.
Розв’язування Обчислимо площу циліндричної випромінюючої поверхні вольфрамової дротини: 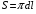 . . Згідно закону Стефана-Больцмана, енергетична світність абсолютно чорного тіла рівна 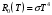 . . Враховуючи закон Кірхгофа для теплового випромінювання в інтегральній формі,  , , маємо, що енергетична світність сірого тіла 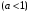 нижча, ніж в абсолютно чорного, та дорівнює нижча, ніж в абсолютно чорного, та дорівнює 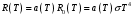 . . З іншого боку, можемо обчислити енергетичну світність вольфрамової спіралі за потужністю теплового випромінювання, що згідно з умовою, дорівнює потужності, споживаній лампою від електромережі 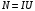 , , та площею випромінюючої поверхні спіралі: 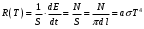 . . Звідси знаходимо температуру спіралі: 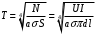 . . Знаходимо числове значення шуканої величини : 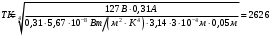 . .Оцінимо довжину хвилі, на якій нитка лампи має максимальну спектральну густину енергетичної світності за законом зміщення Віна: 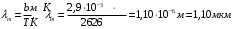 |