|
Лабораторна робота №3 Багатофакторна регресія
БАГАТОФАКТОРНА РЕГРЕСІЯ
Тема роботи: Багатофакторна регресія.
Ціль роботи: Навчитися будувати багатофакторні економетричні моделі, аналізувати їх і будувати прогнозні значення.
ЗАВДАННЯ
На основі статистичних даних показника Y і факторів Х1,Х2,…,Хm вашого варіанту знайти:
кореляційну матрицю і розрахувати визначник для факторної кореляційної матриці;
використовуючи 2-критерій, з надійністю Р=0,95 оцінити наявність загальної мультиколінеарності. Якщо існує загальна мультиколінеарність, то, використовуючи t-статистику, з надійністю Р=0,95 виявити пари факторів, між якими існує мультиколінеарність. Якщо такі пари існують, то один із факторів цієї пари виключити із розгляду;
оцінки параметрів лінійної залежності між показником У та залишившимися факторами Хі;
множинний коефіцієнт кореляції і скорегований індекс множинної детермінації;
використовуючи F- критерій, з надійністю Р=0,95 перевірити статистичну значущість коефіцієнта детермінації (оцінити адекватність прийнятої математичної моделі статистичним даним на основі критерію Фішера);
якщо математична модель із заданою надійністю адекватна експериментальним даним, то використовуючи t-статистику, з надійністю Р=0,95 оцінити значущість параметрів регресії; знайти значення прогнозу показника для заданих значень факторів; з надійністю Р=0,95 обчислити його довірчий інтервал; обчислити частинні коефіцієнти еластичності для точки прогнозу.
На основі отриманих розрахунків зробити економічний аналіз.
ПРИКЛАД РІШЕННЯ ЗАДАЧИ
Нехай дана статистична сукупність спостережень (табл.3.1).
Таблиця 3.1 Початкові дані.
Місяць
|
Прибуток на місяць Y, грн..
|
Фондовіддача Х1, грн
|
Продуктивність праці Х2, грн
|
Питомі інвестиції Х3, грн..
|
1
|
40
|
12
|
5
|
15
|
2
|
45
|
17
|
7
|
18
|
3
|
40
|
13
|
6
|
16
|
4
|
43
|
14
|
7
|
17
|
5
|
48
|
16
|
6
|
20
|
6
|
39
|
15
|
5
|
15
|
7
|
42
|
14
|
6
|
16
|
8
|
45
|
17
|
9
|
18
|
9
|
38
|
12
|
5
|
19
|
10
|
48
|
18
|
10
|
20
|
11
|
50
|
20
|
11
|
22
|
12
|
48
|
17
|
10
|
21
|
13
|
49
|
18
|
12
|
21
|
14
|
45
|
19
|
8
|
20
|
15
|
49
|
20
|
9
|
22
|
16
|
52
|
22
|
14
|
23
|
17
|
54
|
24
|
15
|
24
|
18
|
51
|
21
|
13
|
20
|
19
|
55
|
25
|
16
|
24
|
20
|
56
|
27
|
18
|
25
|
21
|
?
|
19,855
|
10,56
|
21,78
|
На основі статистичних даних показника Y і факторів Х1,Х2,Х3 знайти:
кореляційну матрицю і розрахувати визначник для факторної кореляційної матриці;
використовуючи 2-критерій, з надійністю Р=0,95 оцінити наявність загальної мультиколінеарності. Якщо існує загальна мультиколінеарність, то, використовуючи t-статистику, з надійністю Р=0,95 виявити пари факторів, між якими існує мультиколінеарність. Якщо такі пари існують, то один із факторів цієї пари виключити із розгляду;
оцінки параметрів лінійної залежності між показником У та залишившимися факторами Хі;
множинний коефіцієнт кореляції та скорегований індекс множинної детермінації;
використовуючи F- критерій, з надійністю Р=0,95 перевірити статистичну значущість коефіцієнта детермінації (оцінити адекватність прийнятої математичної моделі статистичним даним на основі критерію Фішера);
якщо математична модель із заданою надійністю адекватна експериментальним даним, то використовуючи t-статистику, з надійністю Р=0,95 оцінити значущість параметрів регресії; знайти значення прогнозу показника для заданих значень факторів; з надійністю Р=0,95 обчислити його довірчий інтервал; обчислити частинні коефіцієнти еластичності для точки прогнозу.
Корреляция'>ХІД РОБОТИ.
Для побудови корелфційної матриці в Excel будемо використовувати інструмент аналізу даних Корреляция. Для цього:
в головному меню послідовно виконаємо команди Сервис – Анализ данных – Корреляция – Ок (якщо інструмент аналізу даних не встановлений, то спочатку виконати послідовність команд Сервис – Надстройки – Пакет анализа – Ок ).
заповнити діалогове вікно Корреляция необхідними параметрами введення мал. 3.1:
Малюнок 3. 1 Діалогове вікно Корреляция
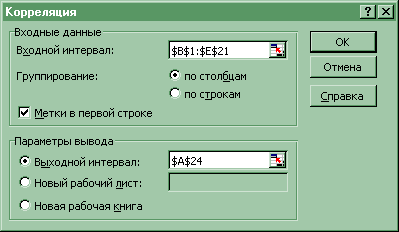 , ,
де Входной интервал – вказується вся область, яка містить початкові статистичні дані, Метки в первой строке – прапорець вказує, що в першому рядку даних знаходяться пояснювальні заголовки, Выходной интервал – вказується адрес комірки, починаючи з якої будуть показані результати.
результати розрахунків – матриці коефіцієнтів парної кореляції – наведені на мал. 3.2:
Малюнок 3. 2 Матриця коефіцієнтів парної кореляції (Кореляційна матриця)
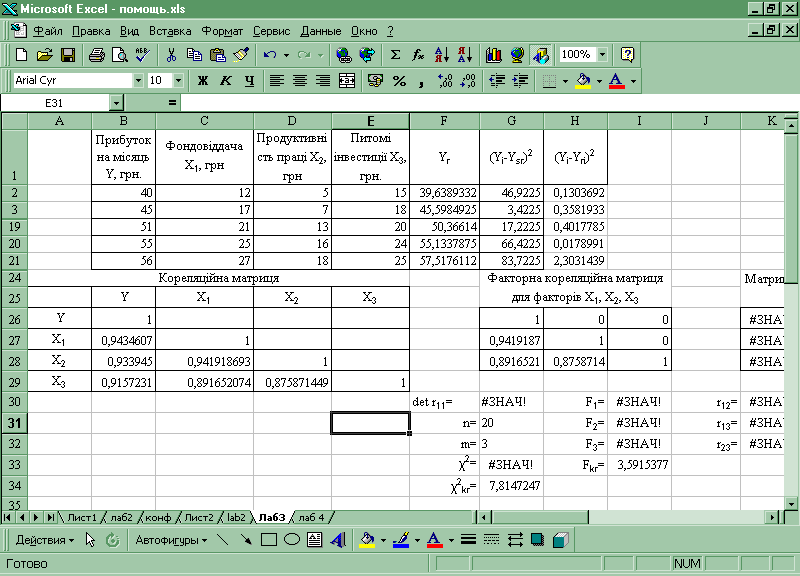
для проведення розрахунків кореляційну матрицю необхідно добудувати. Це можна зробити, використовуючи аппарат Excel копіювання і спеціальну вставку: виділити необхідні комірки – Правка – Копировать – виділити необхідну комірку, починаючи з якої будуть вставлені дані – Правка – Специальная вставка – флажок Транспонировать – Ок мал. 3.3:
Малюнок 3. 3 Кореляційна матриця.
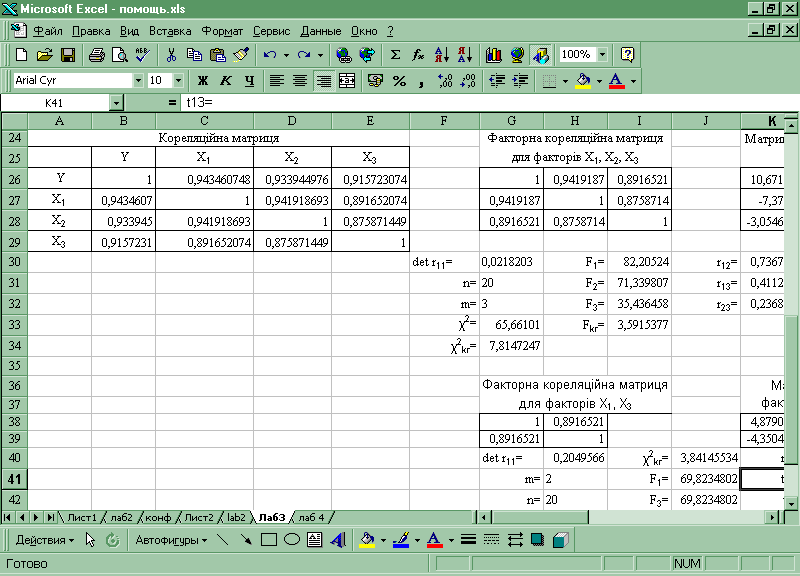
Кореляційна матриця має наступний вигляд:
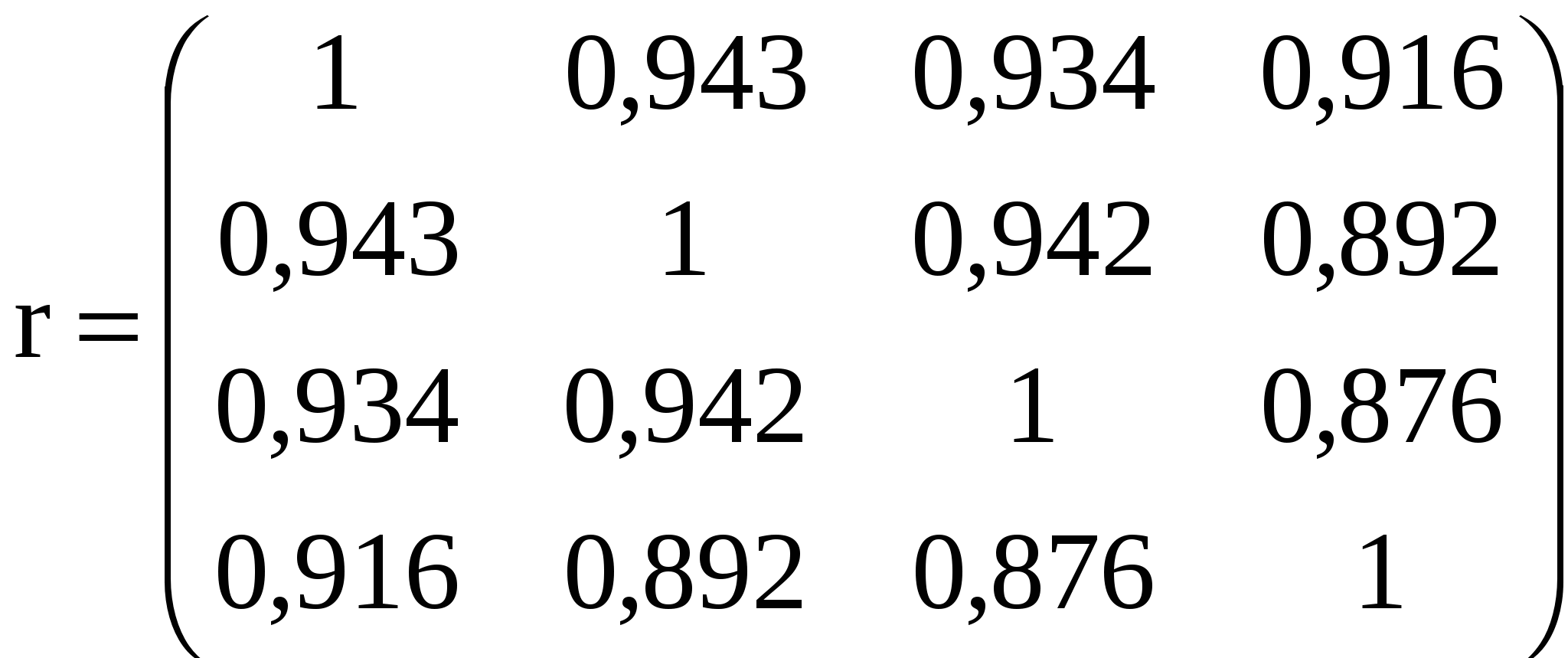 . .
Факторна кореляційна матриця:
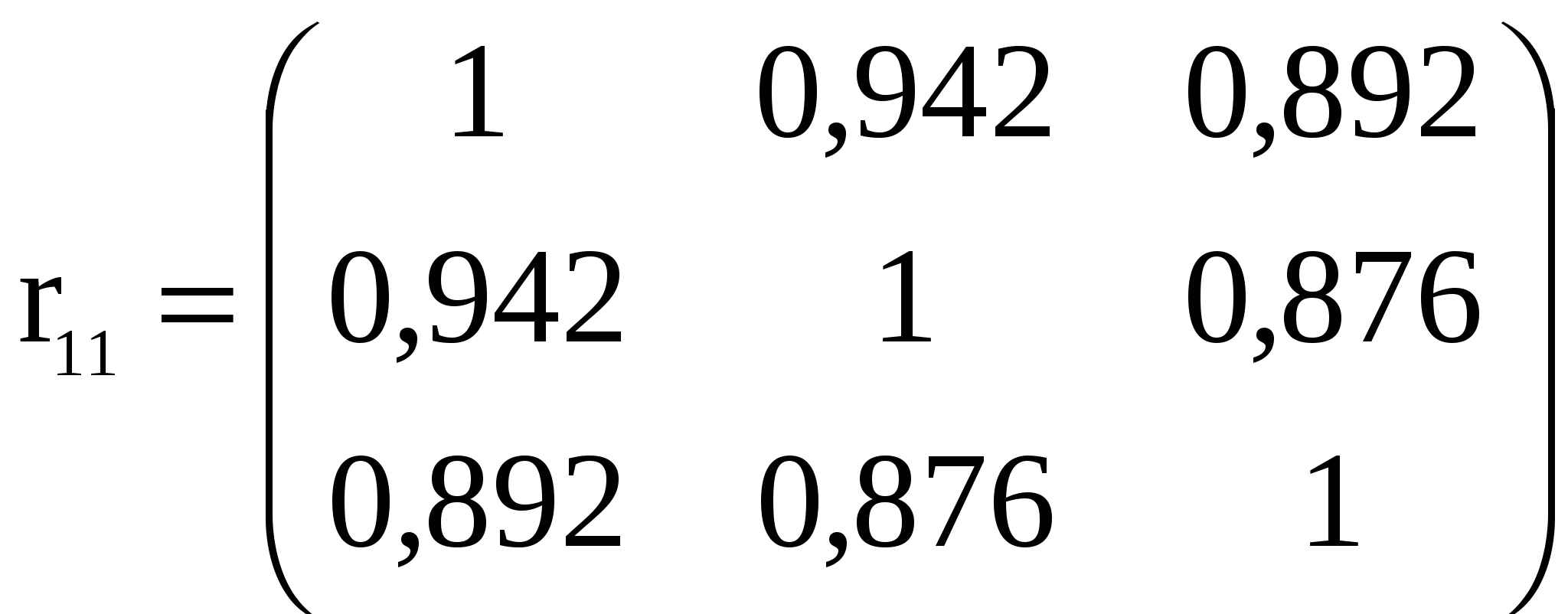 . .
Кожний елемент цієї матриці характеризує щільність зв’язку однієї незалежної змінної з іншою. Оскільки діагональні елементи характеризують щільність зв’язку кожної незалежної змінної з самою собою, то вони дорівнюють одиниці.
Визначник факторної кореляційної матриці можна отримати за допомогою функції МОПРЕД(), в якості аргументів якої необхідно виділяти область значень парних лінійних міжфакторних коефіцієнтів (для приклада, що рішається C26:E28):
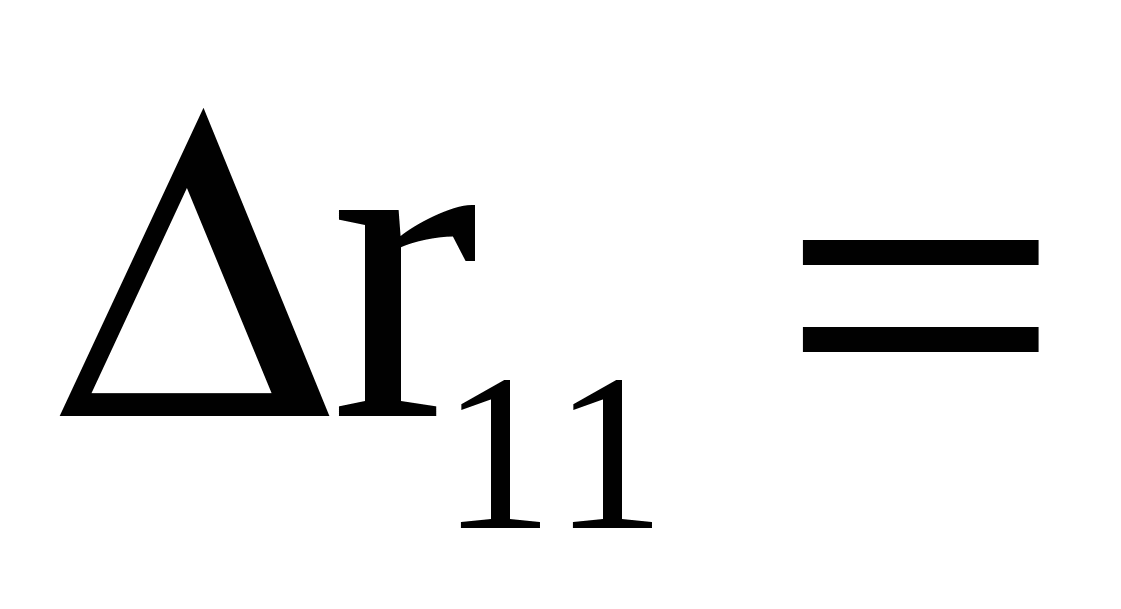 0,02182. 0,02182.
Користуючись елементами факторної кореляційної матриці можна зробити висновок, що між факторами Х1, Х2, Х3 існує зв’язок. Перевіримо, чи є цей зв’язок виявленням мультиколінеарності.
Визначник кореляційної матриці r : 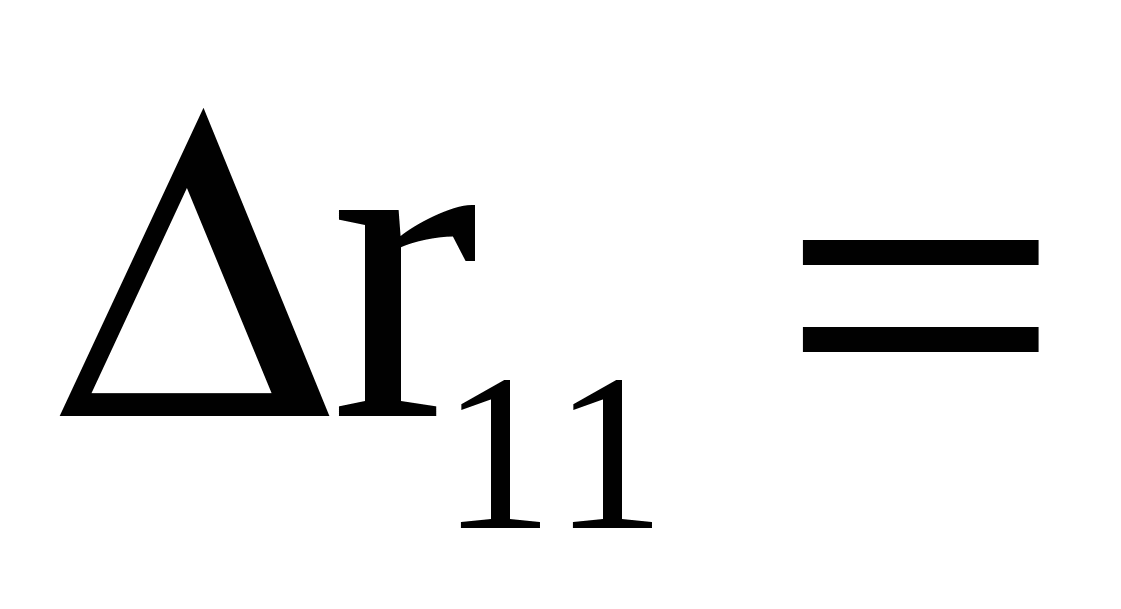 det r11=0,022. Оскільки він наближається до 0, то в масиві пояснюючих змінних може існувати мультиколінеарність. det r11=0,022. Оскільки він наближається до 0, то в масиві пояснюючих змінних може існувати мультиколінеарність.
Обчислимо χ2=-[20-1-(2∙3+5)/6]∙Ln(0,022)=65,66.
При ступені свободи 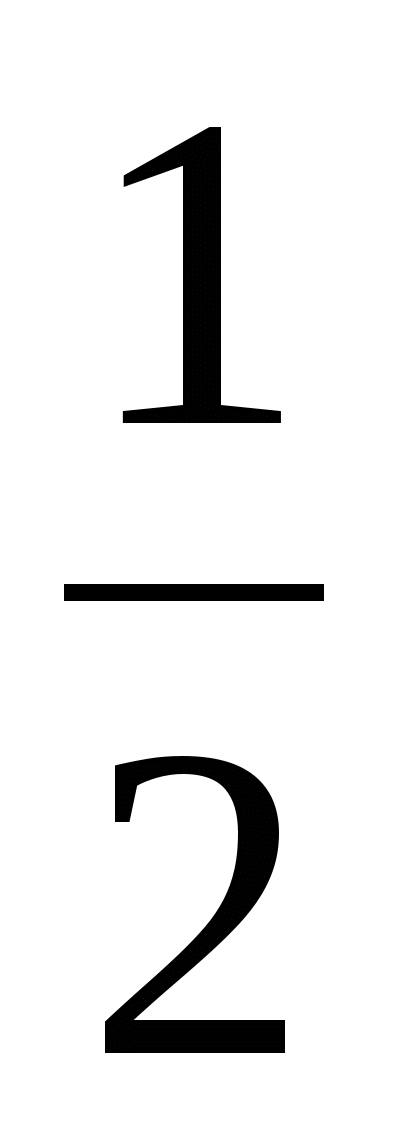 m(m-1)=3 і рівні значущості α=0,05 знаходимо критичне значення, використовуючи функцію ХИ2ОБР() χ2кр=7,8. Оскільки χ2> χ2кр, то в масиві пояснювальних змінних (продуктивність праці, питомі інвестиції та фондовіддача) існує мультиколінеарність. m(m-1)=3 і рівні значущості α=0,05 знаходимо критичне значення, використовуючи функцію ХИ2ОБР() χ2кр=7,8. Оскільки χ2> χ2кр, то в масиві пояснювальних змінних (продуктивність праці, питомі інвестиції та фондовіддача) існує мультиколінеарність.
Знайдемо матрицю, обернену до факторної кореляційної матриці, використовуючи функцію МОБР(). Для використання цієї функкції виконують наступні кроки:
Виділяють область комірок, де будуть розташовані значення результату виконання цієї функції, скільки значень – стільки комірок;
Використовуючи Мастер функций (Вставка – Функция) викликають функцію МОБР() і заповнюють її параметри, виділяючи область комірок, де знаходяться значення факторної кореляційної матриці;
Натискають послідовність клавіш Ctrl – Shift – Enter,
C=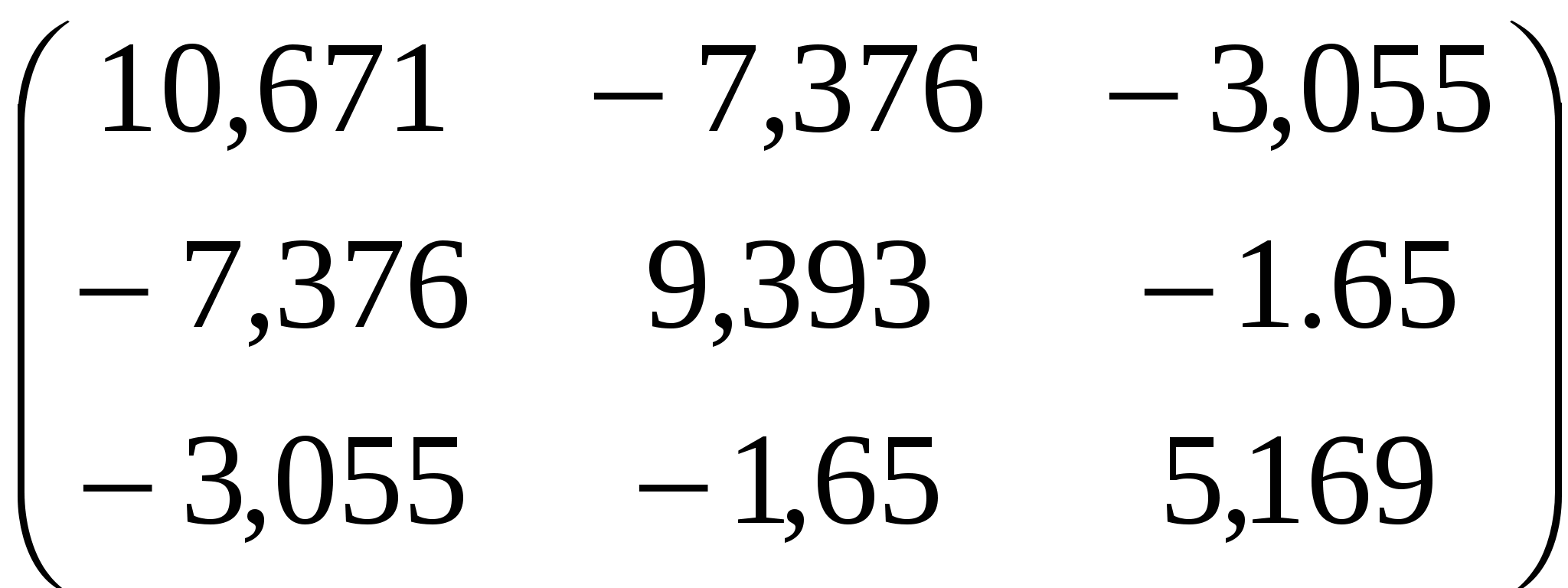 . .
Використовуючи діагональні елементи матриці С обчислимо F – критерії:
F1=(c11-1)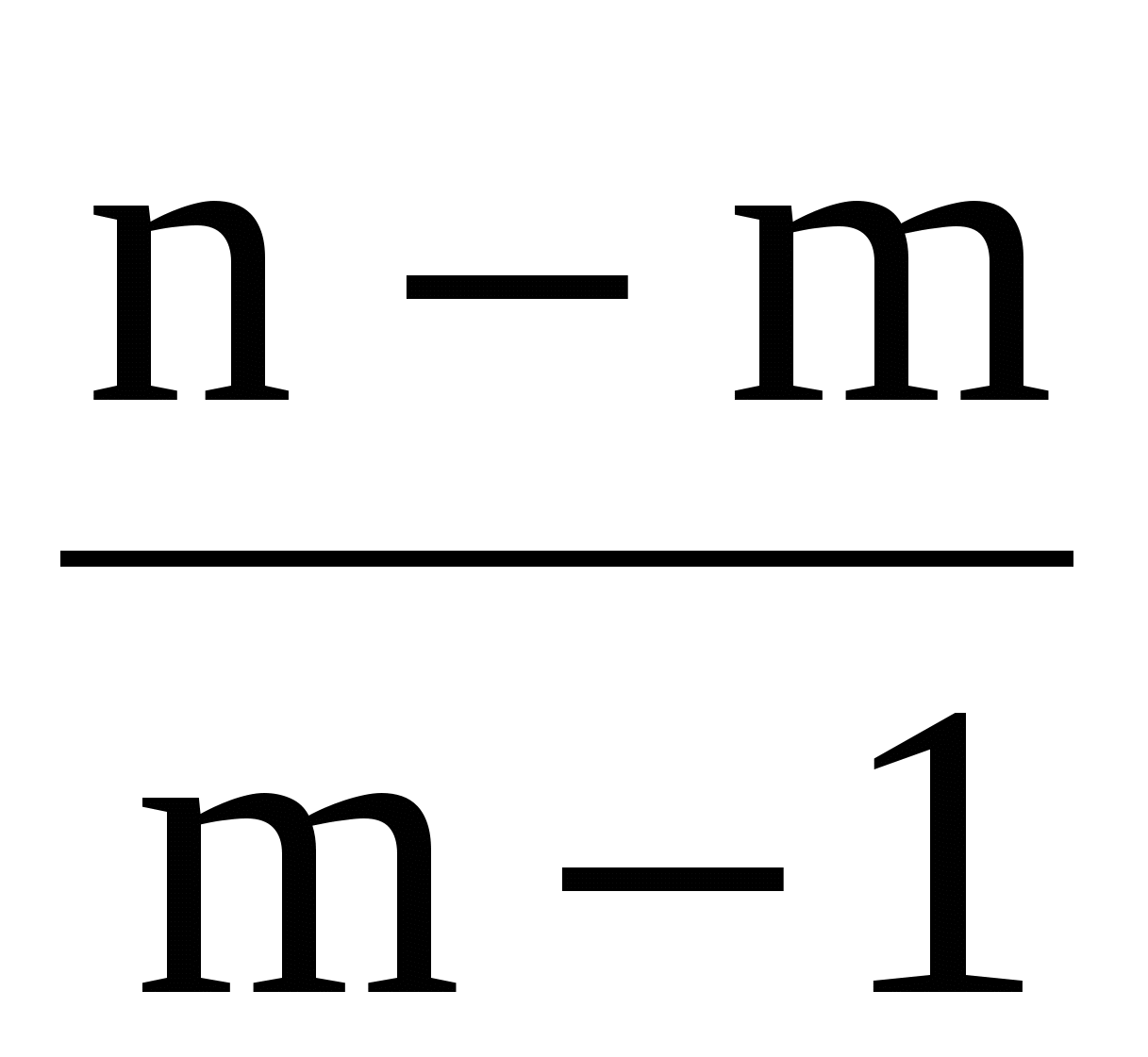 =(10,67-1) =(10,67-1)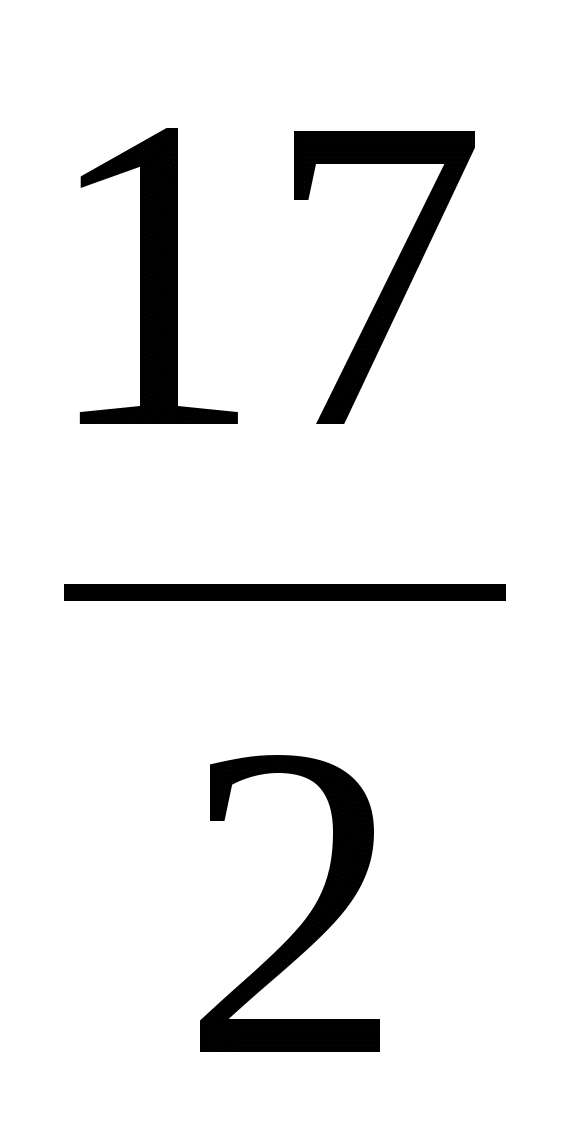 =82,21; =82,21;
F2=(c22-1)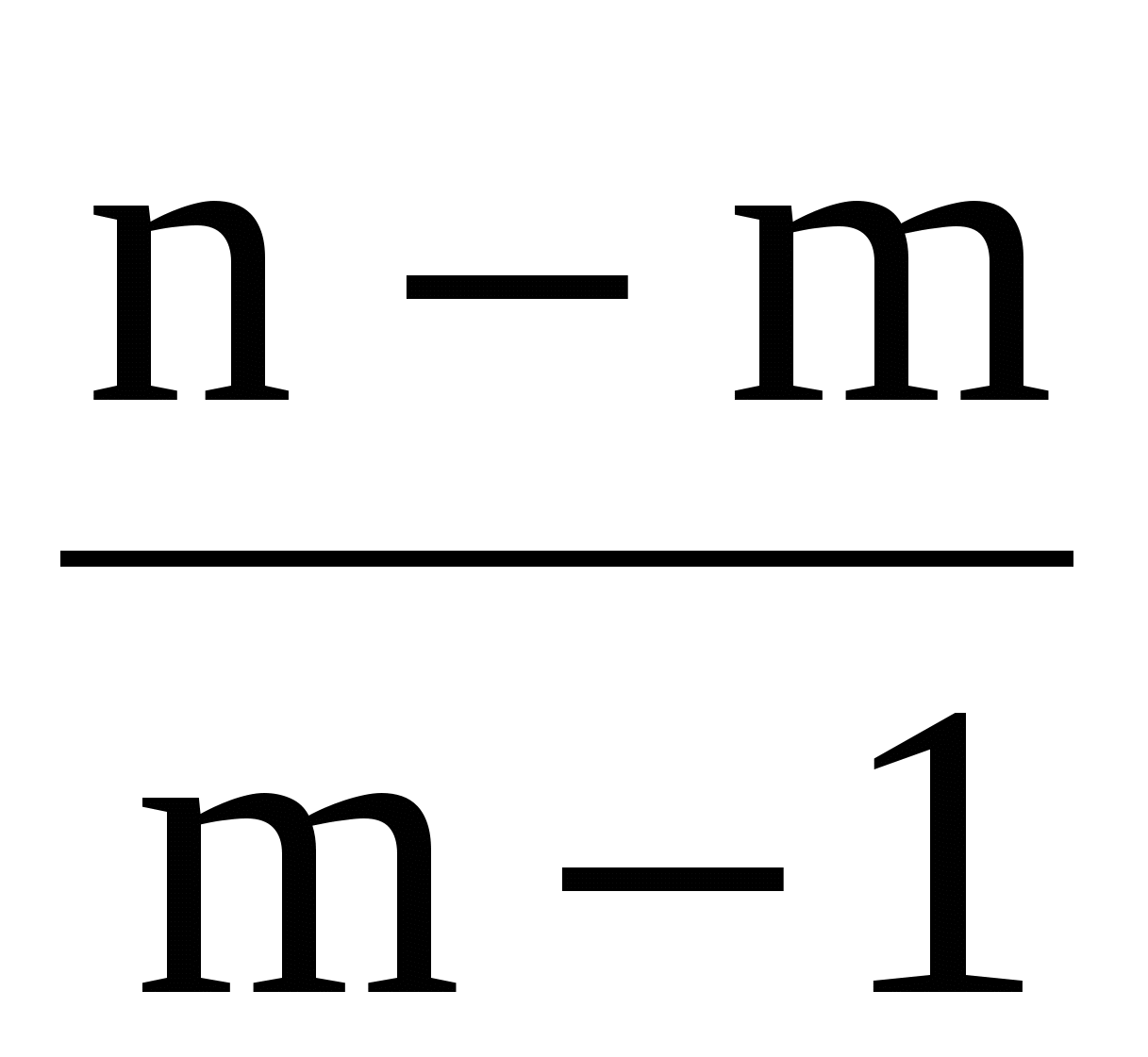 =(9,39-1) =(9,39-1)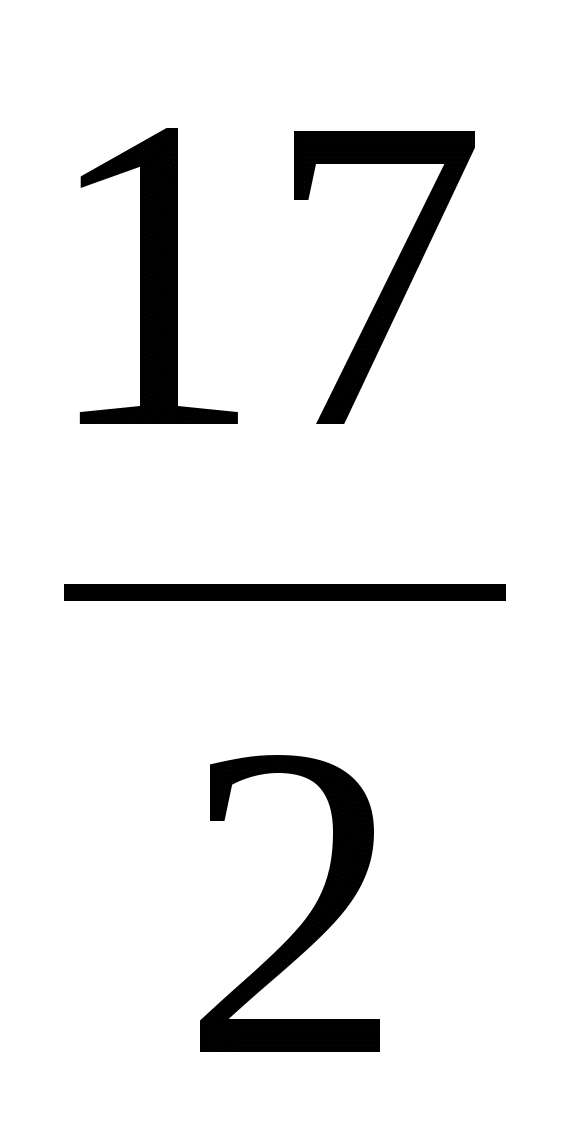 =71,34; =71,34;
F3=(c33-1)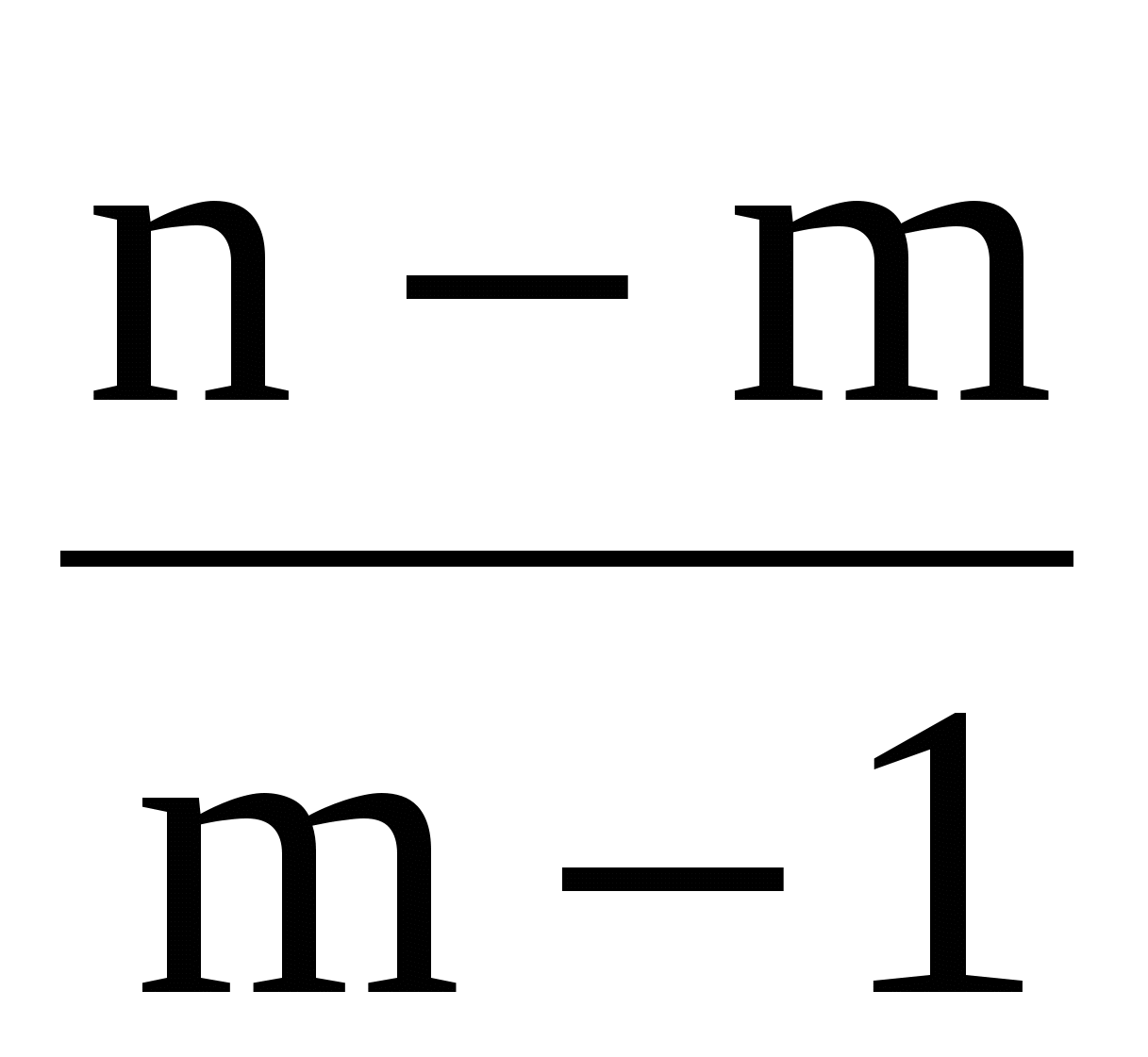 =(5,169-1) =(5,169-1)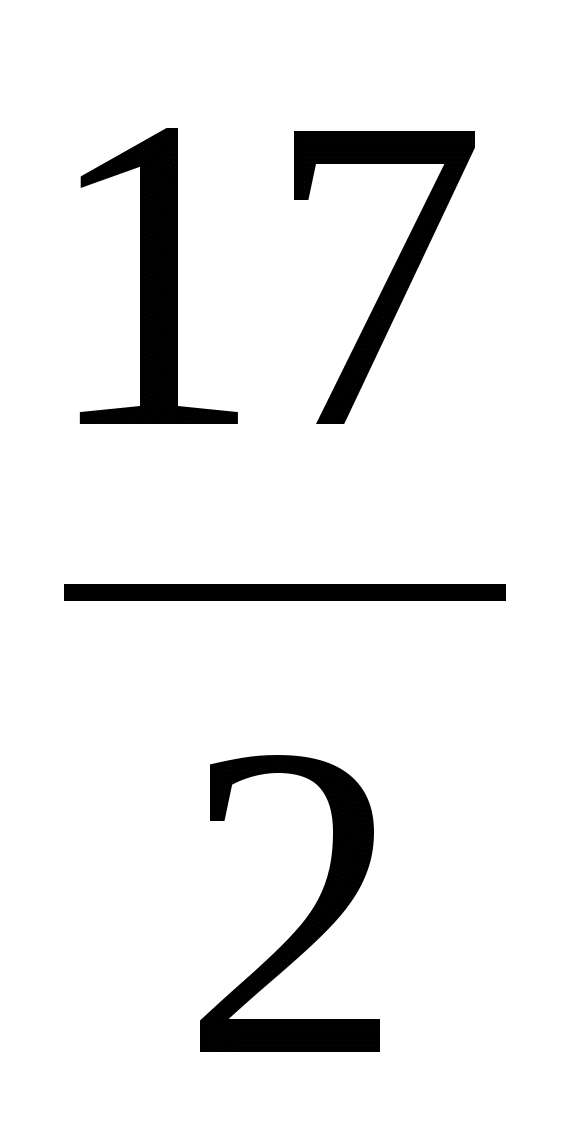 =35,44. =35,44.
Для рівня значущості α=0,05 і ступені вільності m-1=2 і n-m=17 критичне (табличне) значення критерію (функція FРАСПОБР()) Fкр.=3,59. Оскільки кожне з розрахованих значень Fi більше ніж критичне, то кожна з пояснювальних змінних мультиколінеарна з іншими.
Використовуючи елементи матриці С, обчислимо часткові коефіцієнти кореляції:
r12=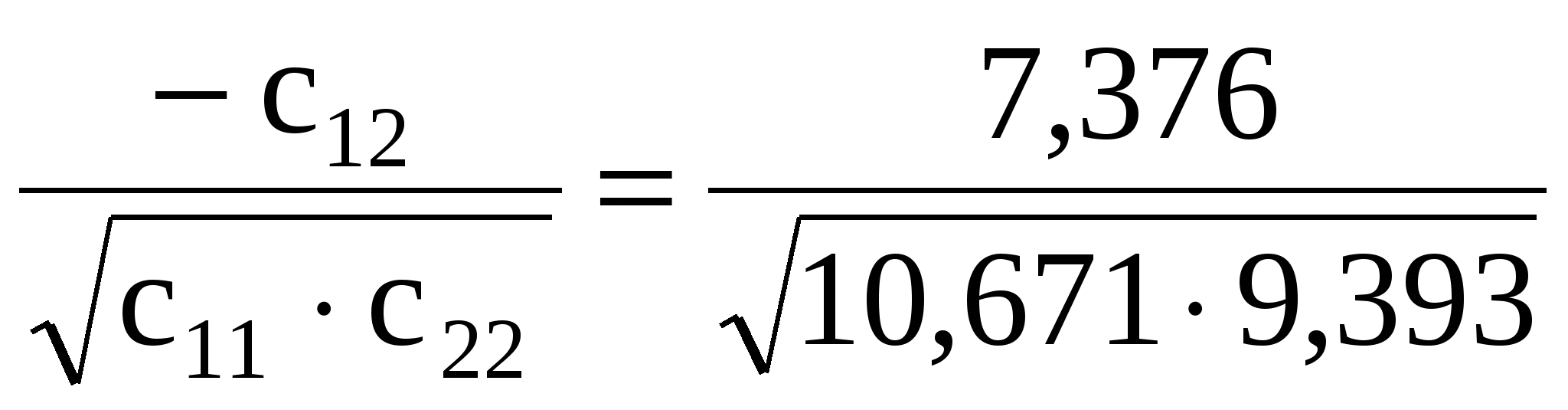 =0,737; =0,737;
r13=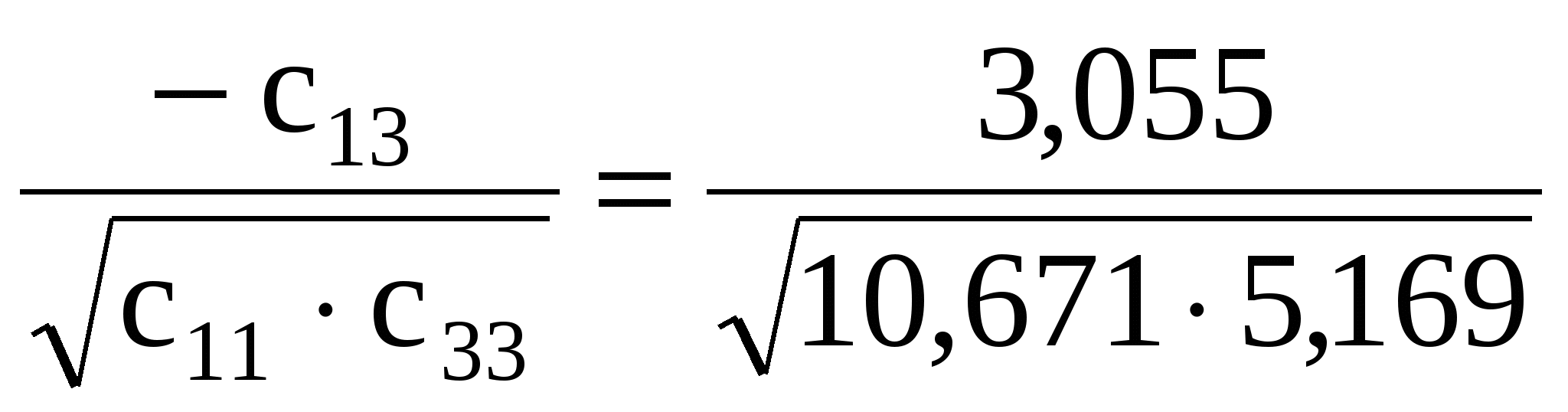 =0,411; =0,411;
r23=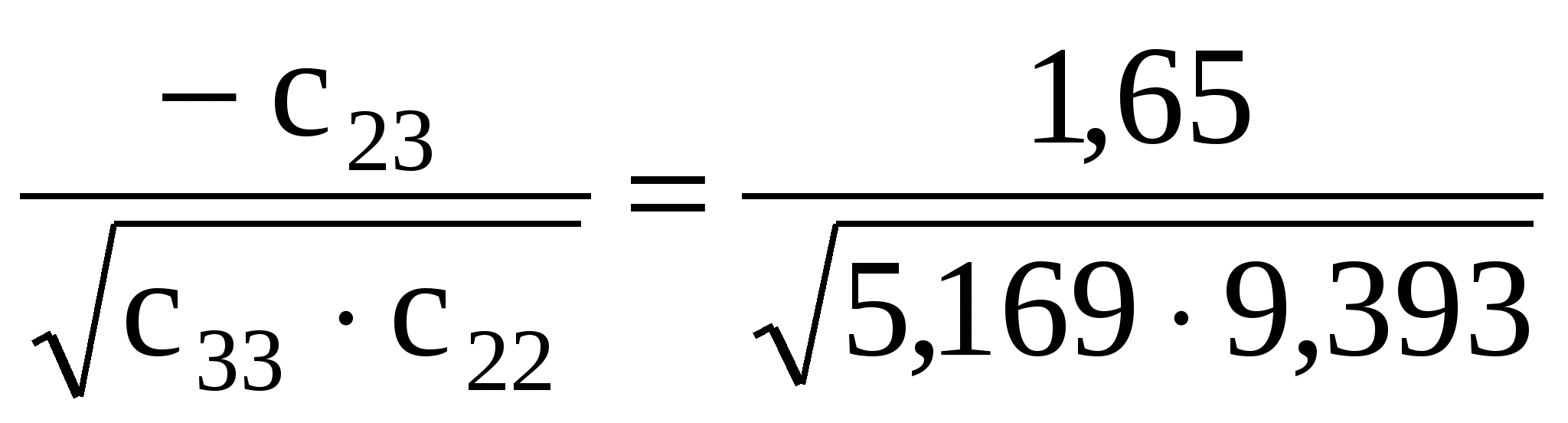 =0,237. =0,237.
Порівнявши часткові коефіцієнти кореляції з парними (кореляційна матриця), можна помітити, що частинні коефіцієнти значно менш за парні. Це ще раз показує, що на підставі парних коефіцієнтів кореляції не можна зробити висновків про наявність або відсутність мультиколінеарності.
Визначимо t – критерії на основі частинних коефіцієнтів кореляції:
t12=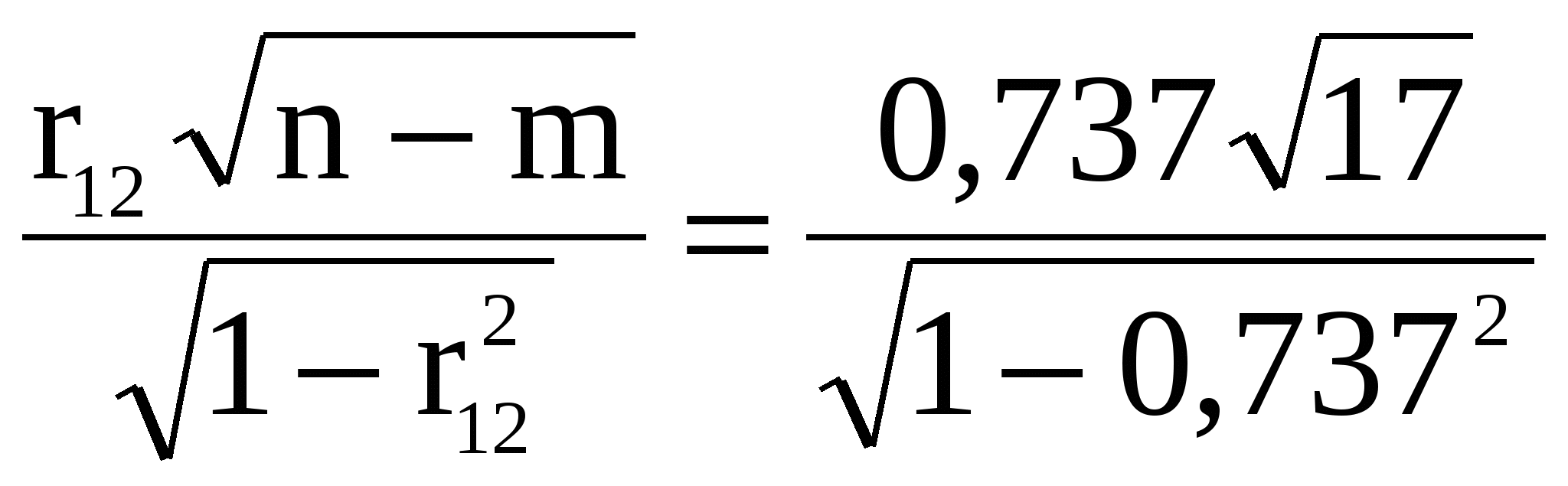 =4,49; =4,49;
t13=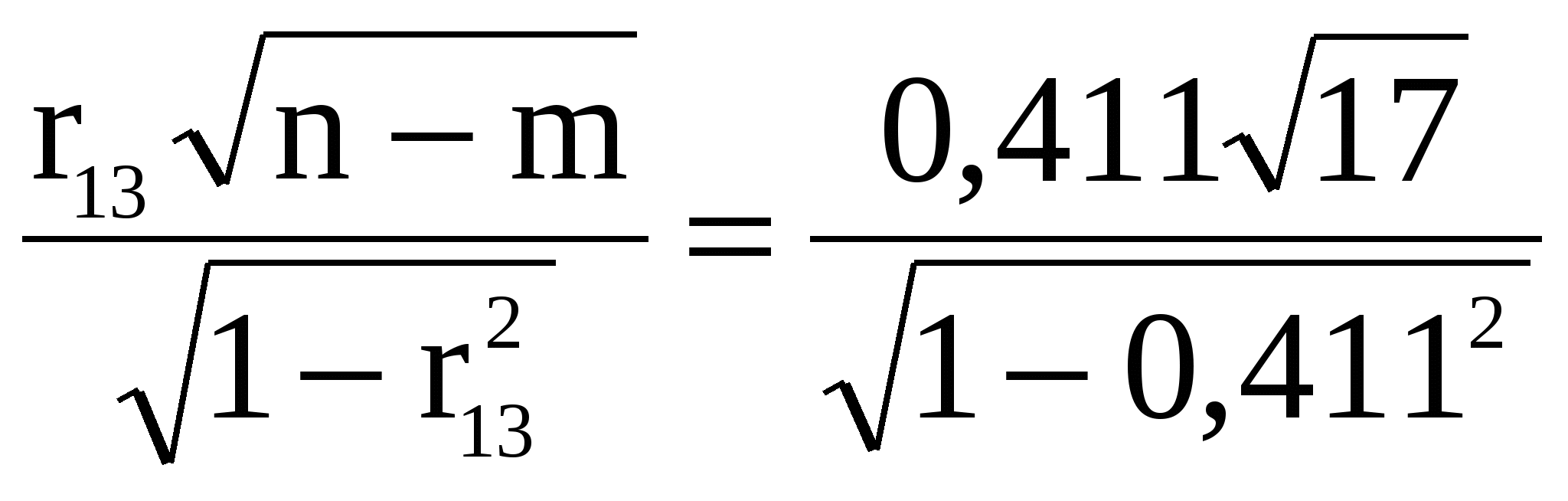 =1,86; =1,86;
t23=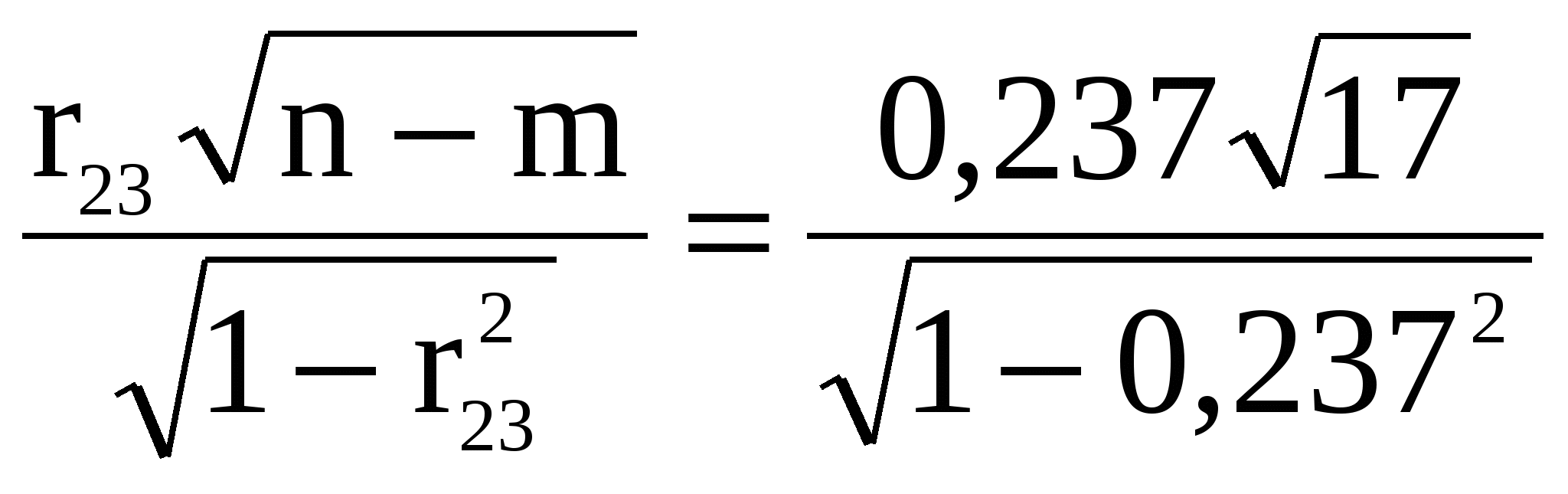 =1,005. =1,005.
Табличне значення t – критерію при n-m=17 ступенях вільності і рівні значущості 0,05 дорівнює 2,12 (функція СТЬЮДРАСПОБР()). Звідси виходить, що лише для пари факторів Х1 і Х2 існує мультиколінеарність. Розрахував вибіркові коефіцієнти кореляції, що пов’язують пояснювальні фактори з залежним Y, знайдемо 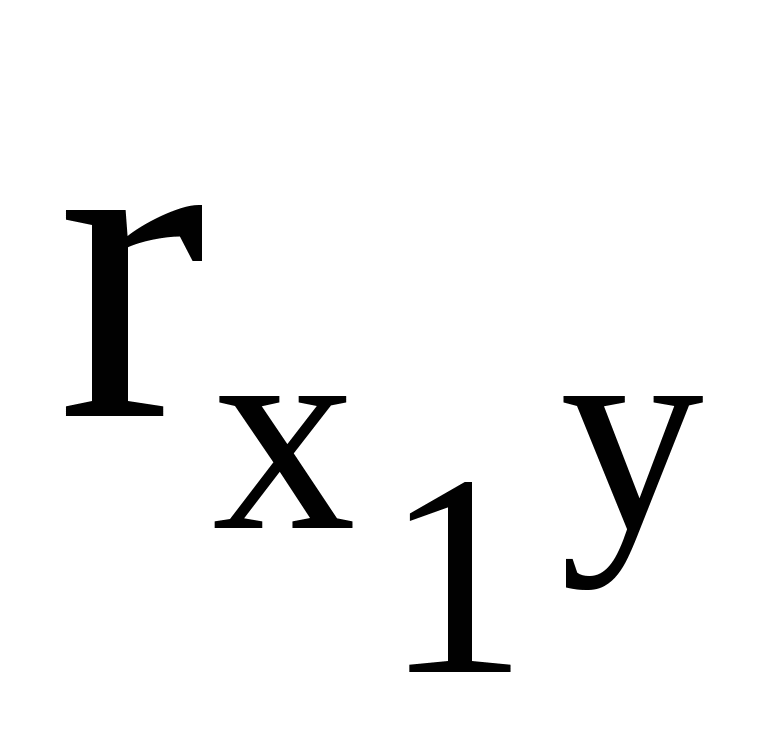 =0,944, =0,944, 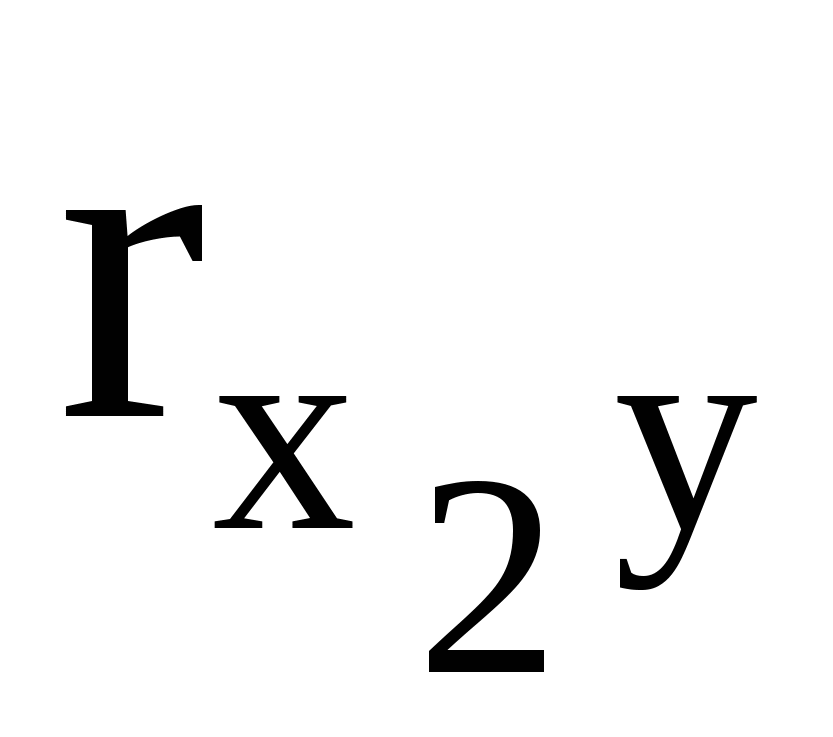 =0,934, оскільки =0,934, оскільки 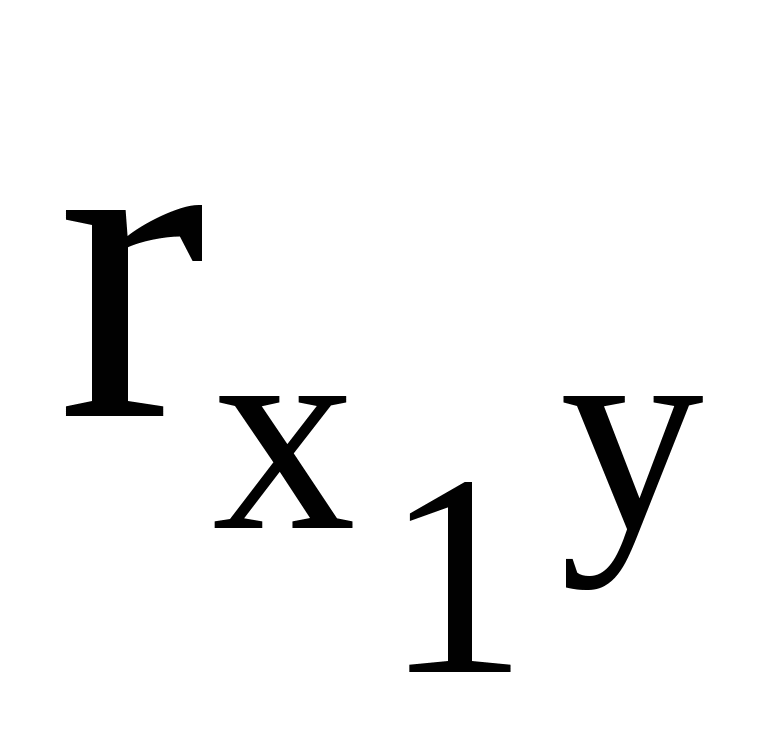 > >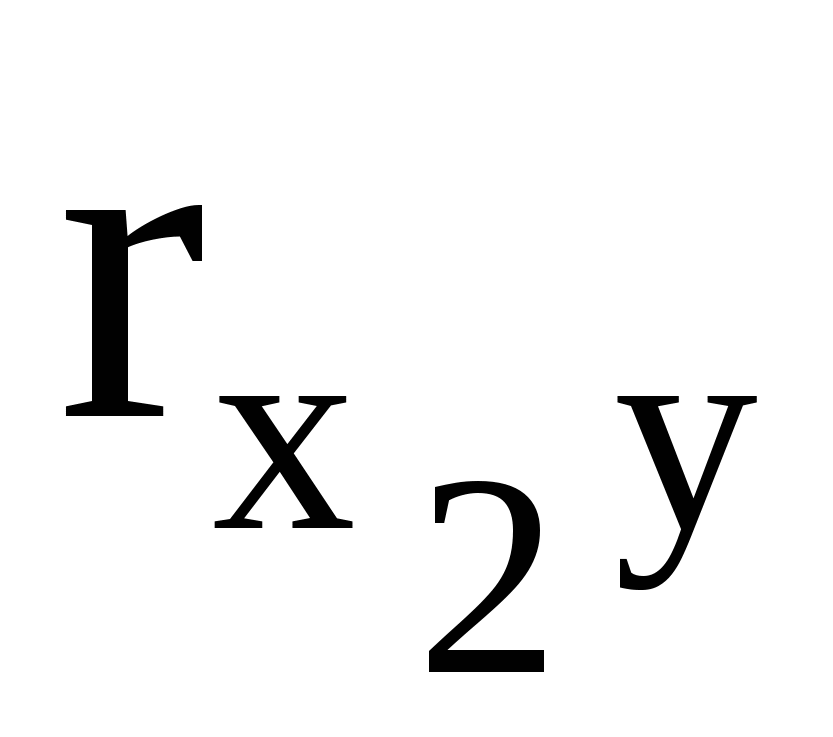 , з моделі виключаємо фактор X2. , з моделі виключаємо фактор X2.
Знайдемо кореляційну матрицю факторів Х1 і Х3:
r=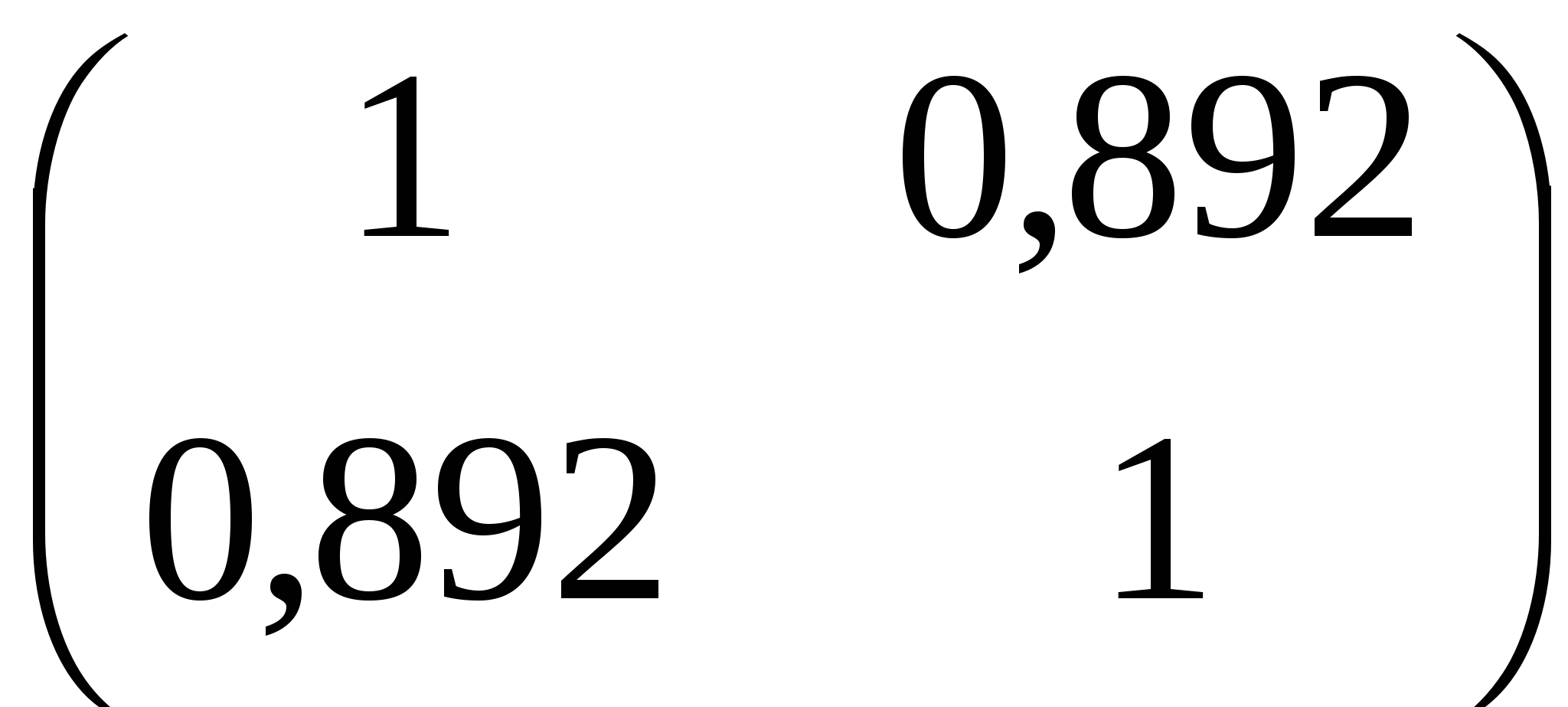 . .
Обернена матриця:
C=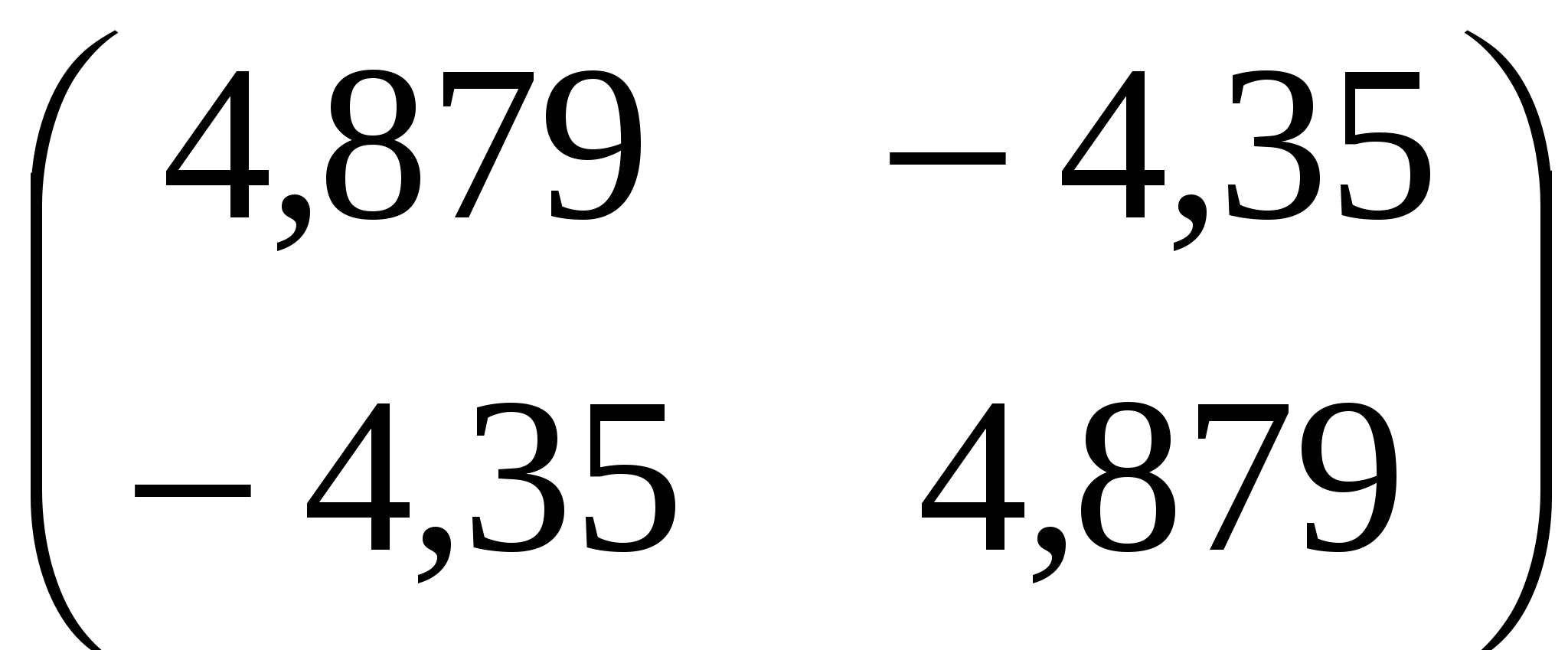 . .
Значення χ2=27,74 більше ніж χ2кр = 3,8. Це значить, що між факторами X1 і X3 існує мультиколінеарність. Це підтверджує і значення t – статистики:
r13=0,8917, t13=8,356,
оскільки воно більш ніж 2,11. Тобто з моделі необхідно виключити ще один з факторів. Оскільки 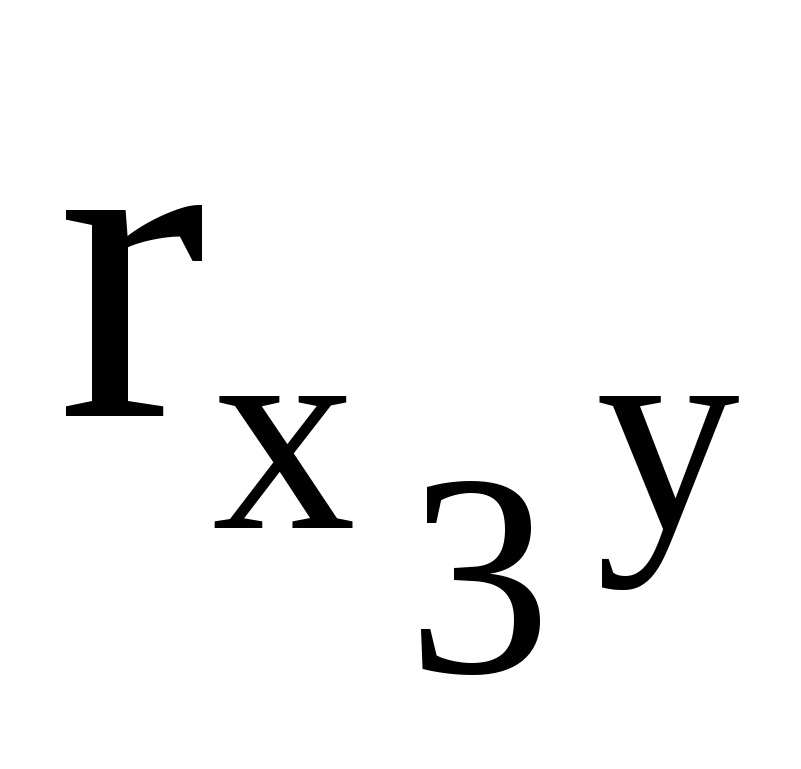 =0,916< =0,916<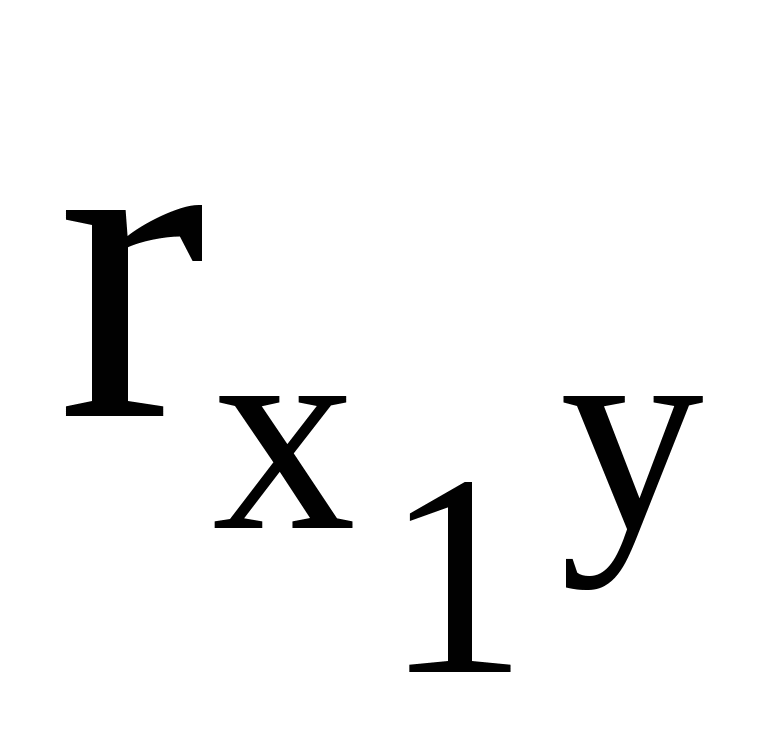 =0,944, то таким фактором є фактор X3. =0,944, то таким фактором є фактор X3.
Отже з моделі виключили два фактори X2 і X3.
Зауваження: Якщо при перевірці наявності мультиколінеарності визначається зв’язок, наприклад, між парами факторів Х1 і Х2 та Х2 і Х3, то з розгляду виключається той фактор, який приймає участь одночасно в першій та другій парах. Так для нашого приклада таким фактором є Х2.
Припустимо, що між показником Y і фактором X1 існує лінійна залежність:
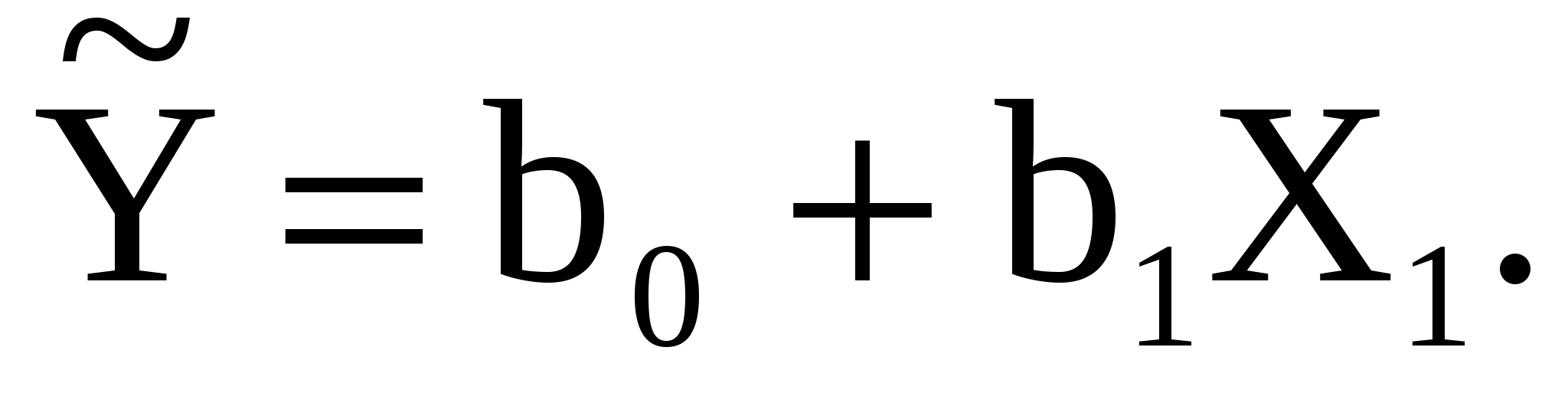
Знайдемо оцінки параметрів, використовуючи матричні операції: 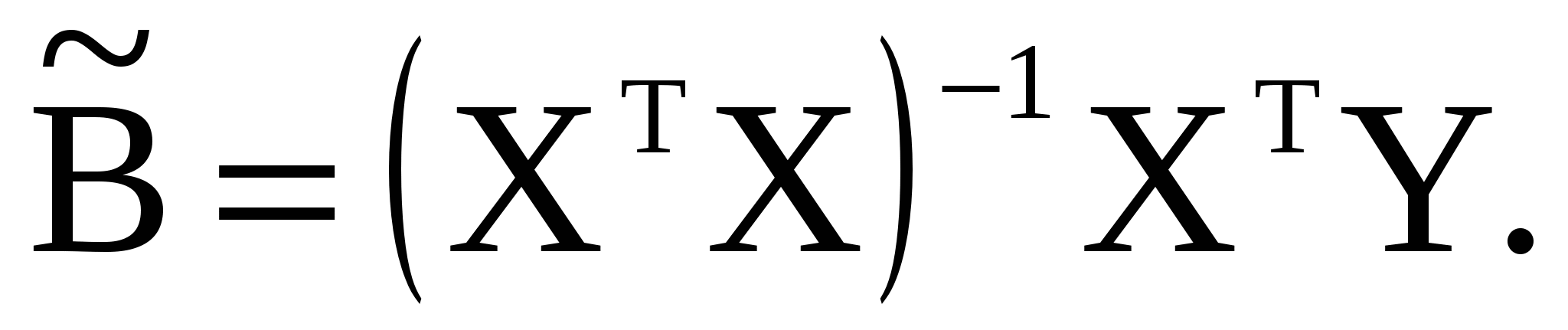 Перш ніж проводити розрахунки добавимо до залишившихся факторних значень стовпчик, який містить одиниці. Їх кількість повинна дорівнювати обсягу вибірки, тобто n: Перш ніж проводити розрахунки добавимо до залишившихся факторних значень стовпчик, який містить одиниці. Їх кількість повинна дорівнювати обсягу вибірки, тобто n:
Малюнок 3. 4 Вигляд матриці кінцевої матриці Х
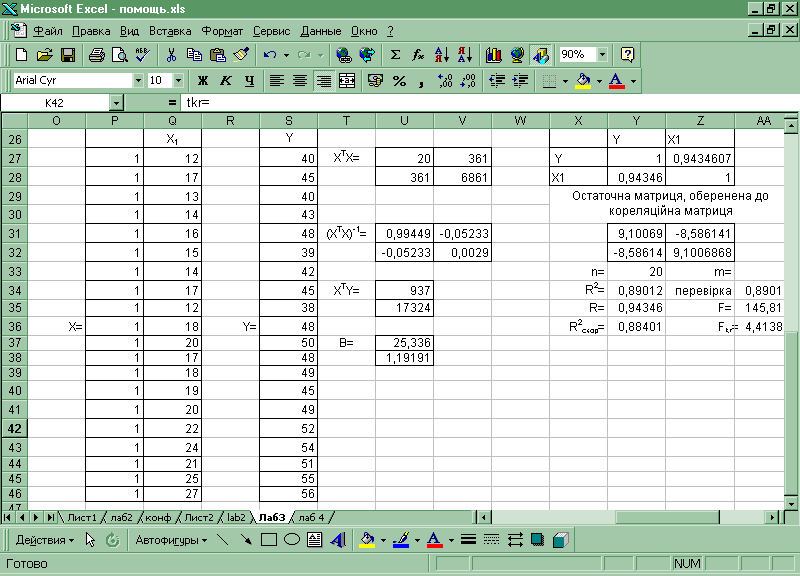
Для розрахунків викоритсовуються функціїї:
МОБР() – для знаходження зворотньої матриці,
МУМНОЖ() – для знаходження добутку двох матриць.
Дії з цими функціїї відповідні діям, що описані вище для функції МОБР().
Всі необхідні дії виконані нижче:
Малюнок 3. 5 Розрахунки параметрів моделі.

Для матричних розрахунків в Excel використовувались наступні формули:
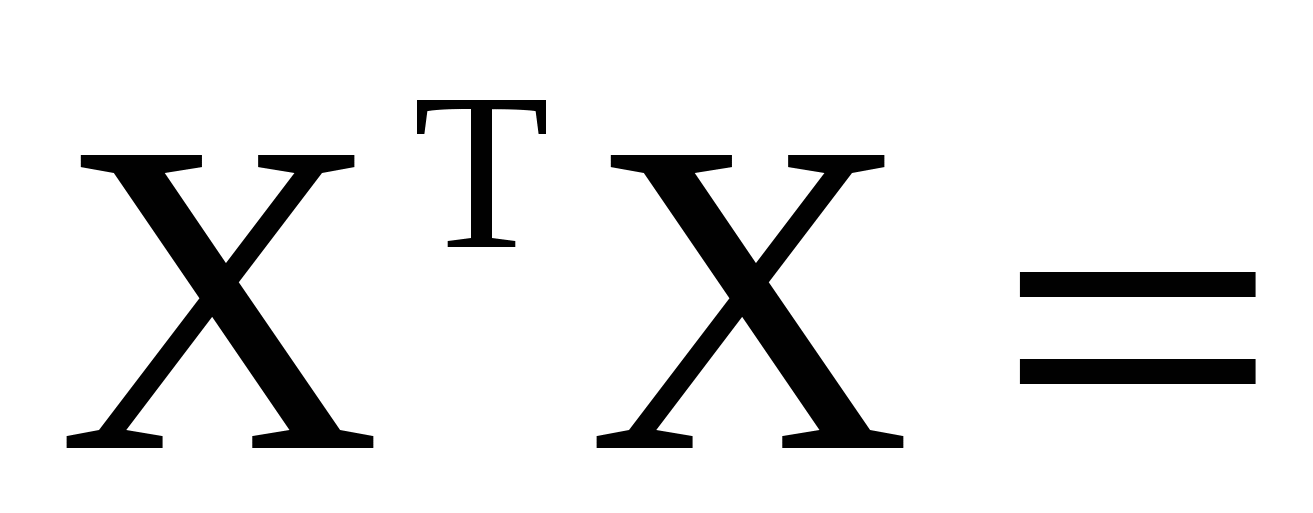 МУМНОЖ(ТРАНСП(P27:Q46);P27:Q46); МУМНОЖ(ТРАНСП(P27:Q46);P27:Q46);
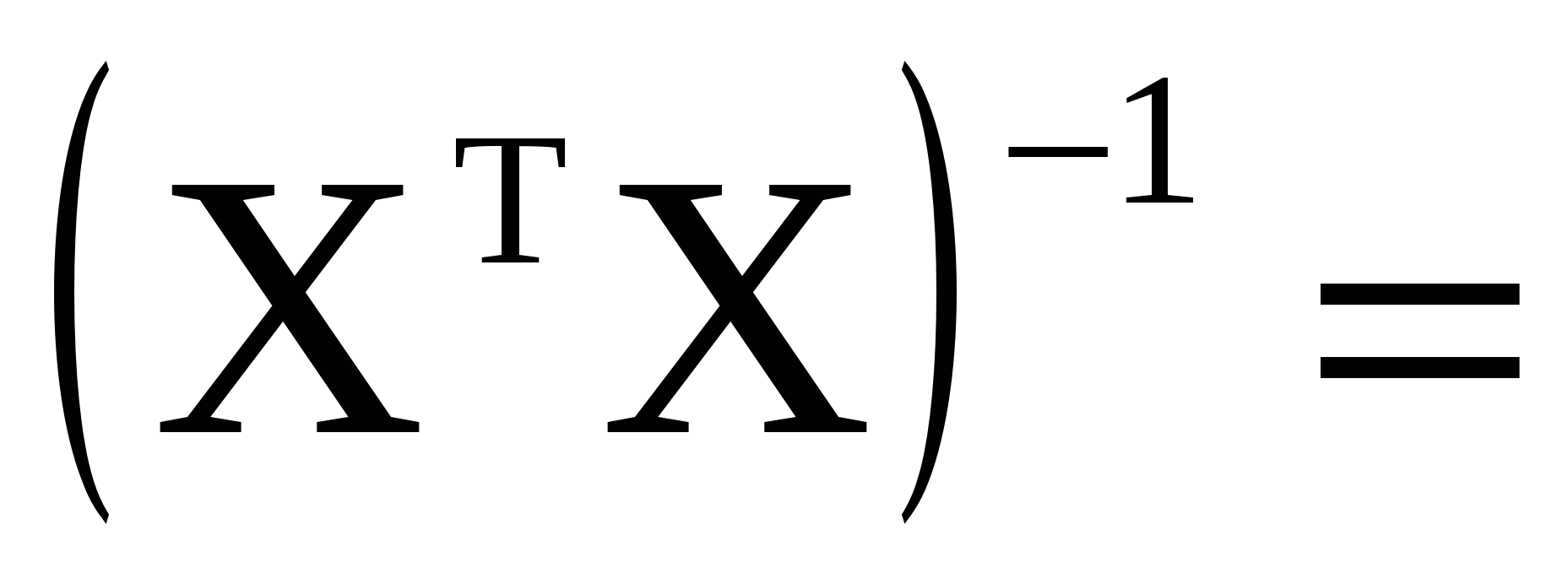 МОБР(U27:V28); МОБР(U27:V28);
 МУМНОЖ(ТРАНСП(P27:Q46);S27:S46); МУМНОЖ(ТРАНСП(P27:Q46);S27:S46);
B=МУМНОЖ(U31:V32;U34:U35).
Отже економетрична модель має вигляд: 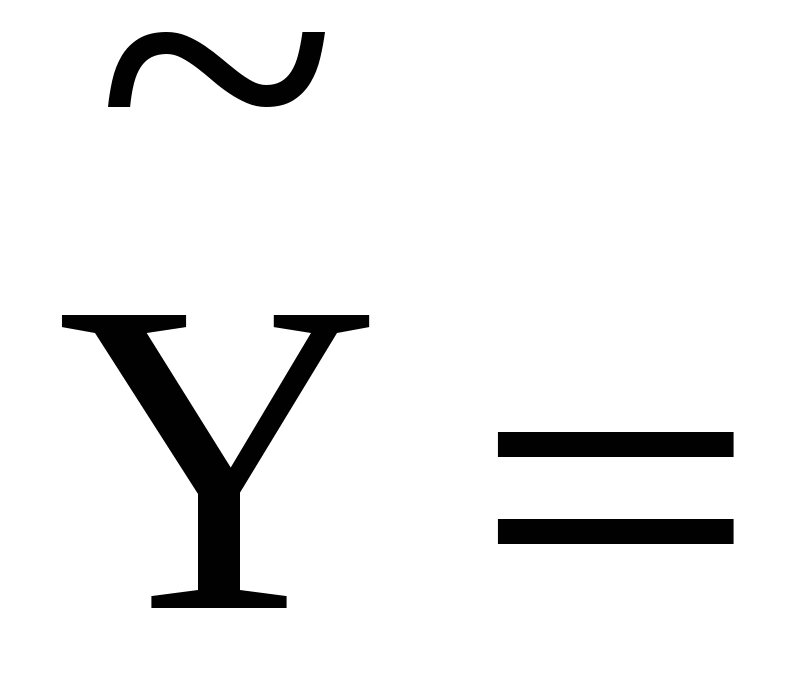 25,336+1,192X1. 25,336+1,192X1.
Коефіцієнт детермінації знайдемо на основі матриці оберненої до розширеної кореляційної матриці (кореляційної матриці) (вона містить парні вибіркові коефіцієнти кореляції не тільки між пояснювальними змінними, але й У):
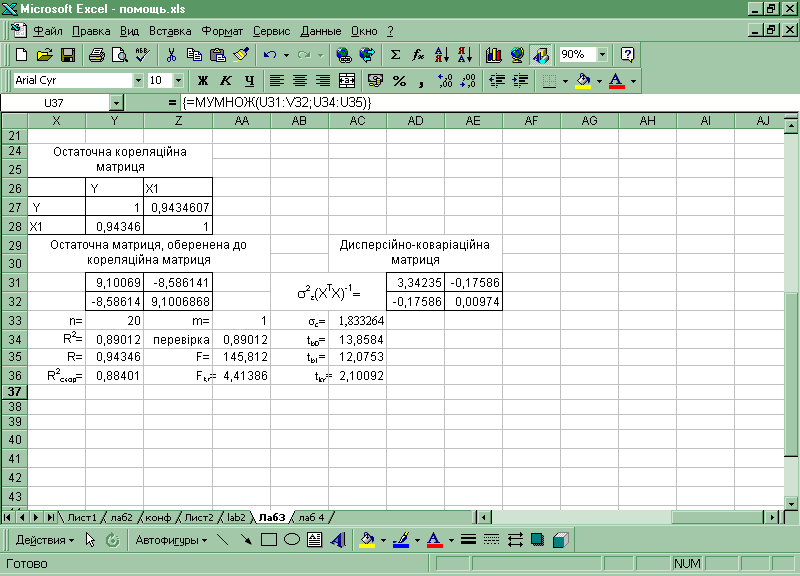
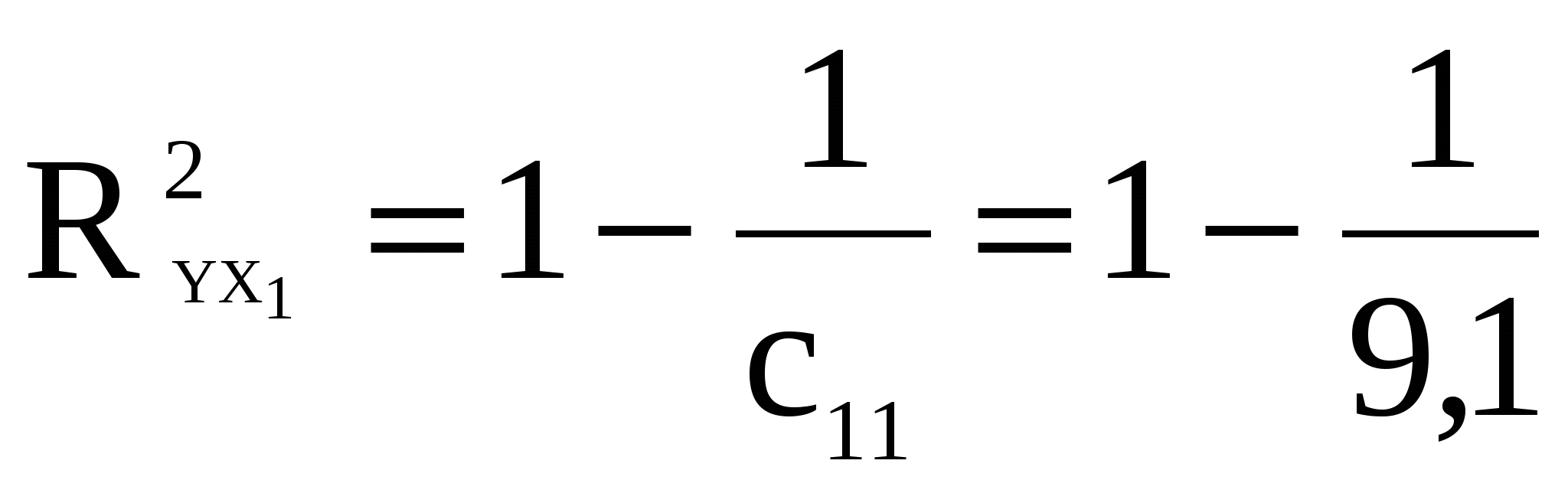 =0,89. =0,89.
Для розрахунку множинного коефіцієнта детермінації можна використовувати формулу:
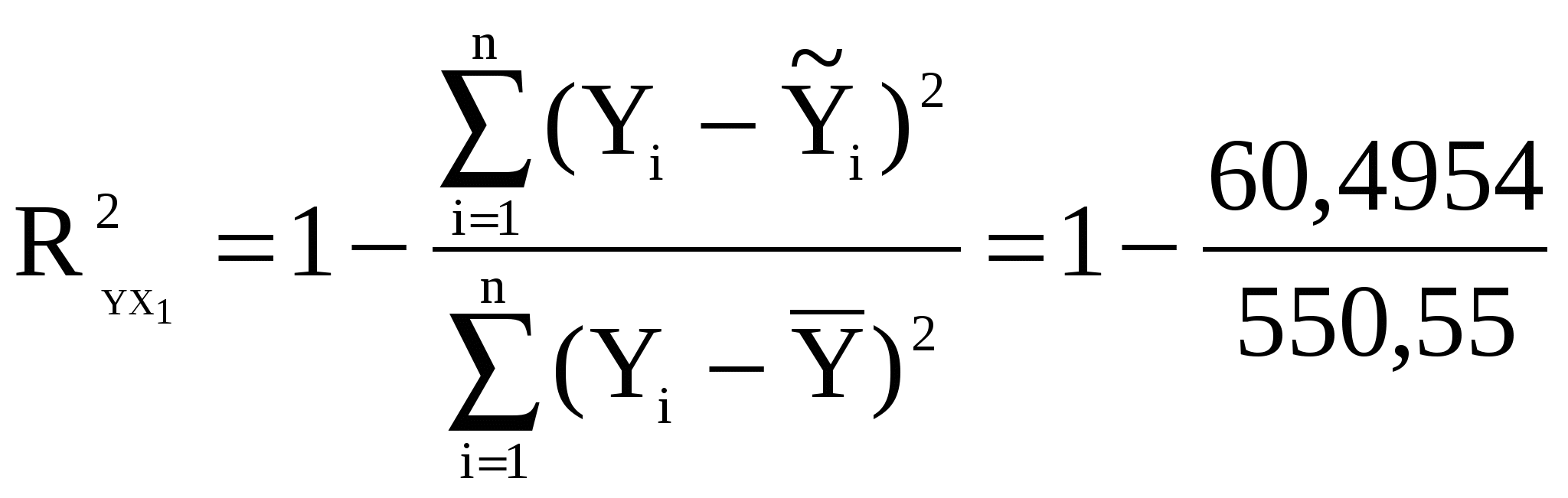 =0,89. =0,89.
Множиний коефіцієнт кореляції 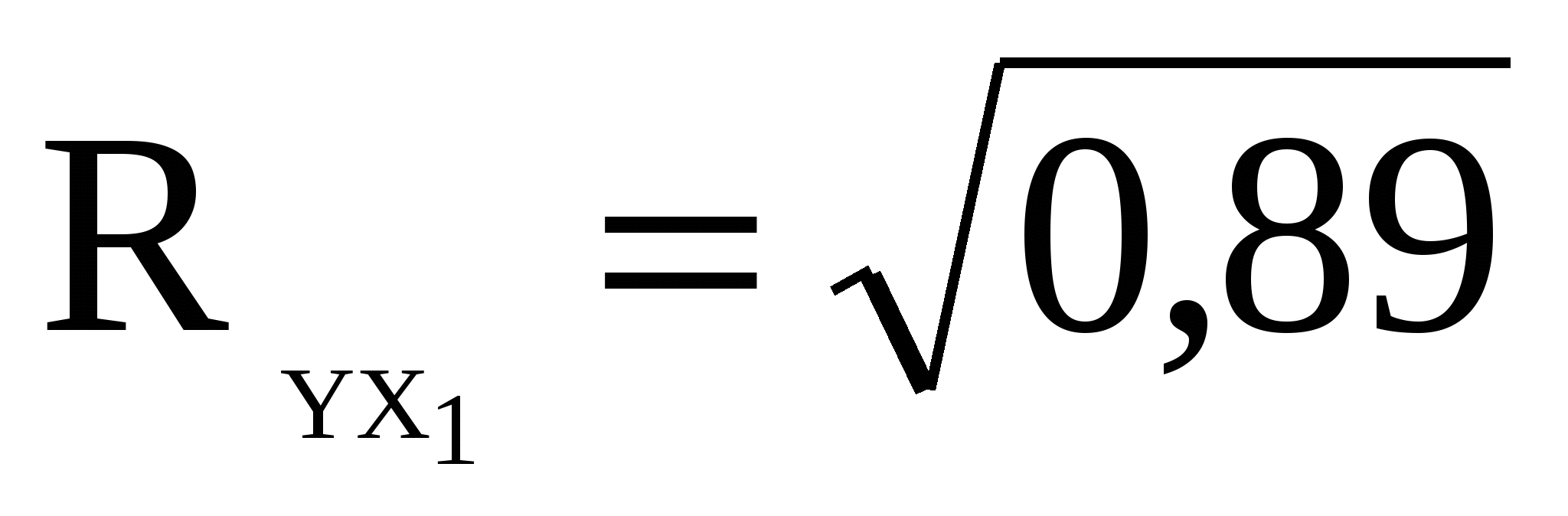 =0,943. =0,943.
Скорегований коефіцієнт (індекс) множинної детермінації розраховується за формулою:
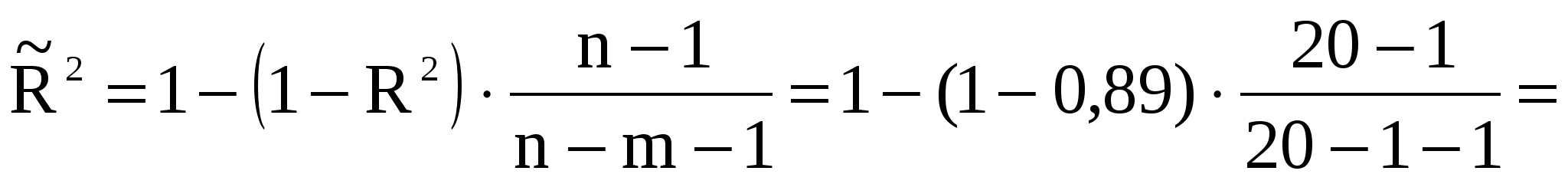 0884, 0884,
Розрахуємо значення F – критерію:
FR=(c11-1)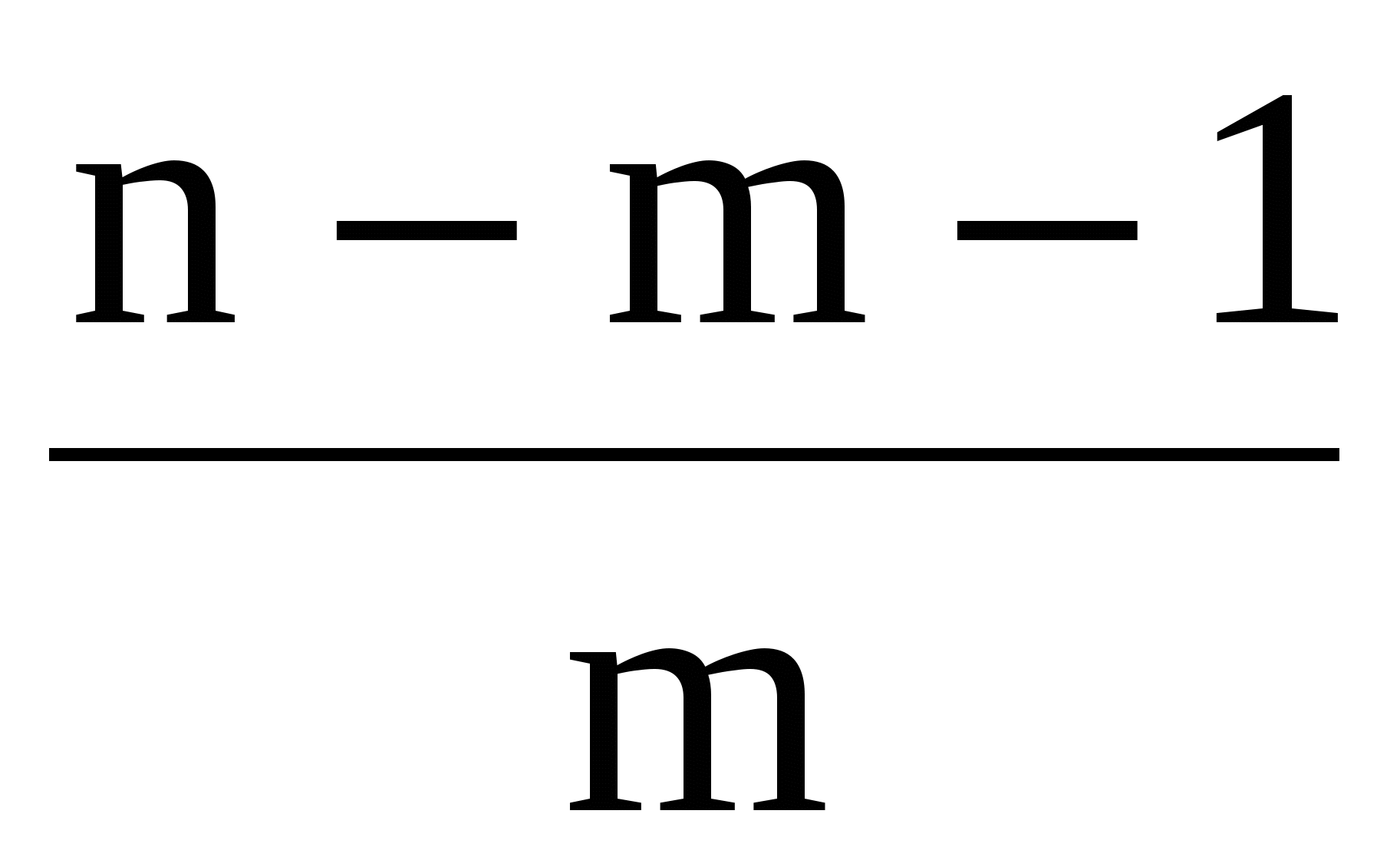 =(9,1 - 1) =(9,1 - 1)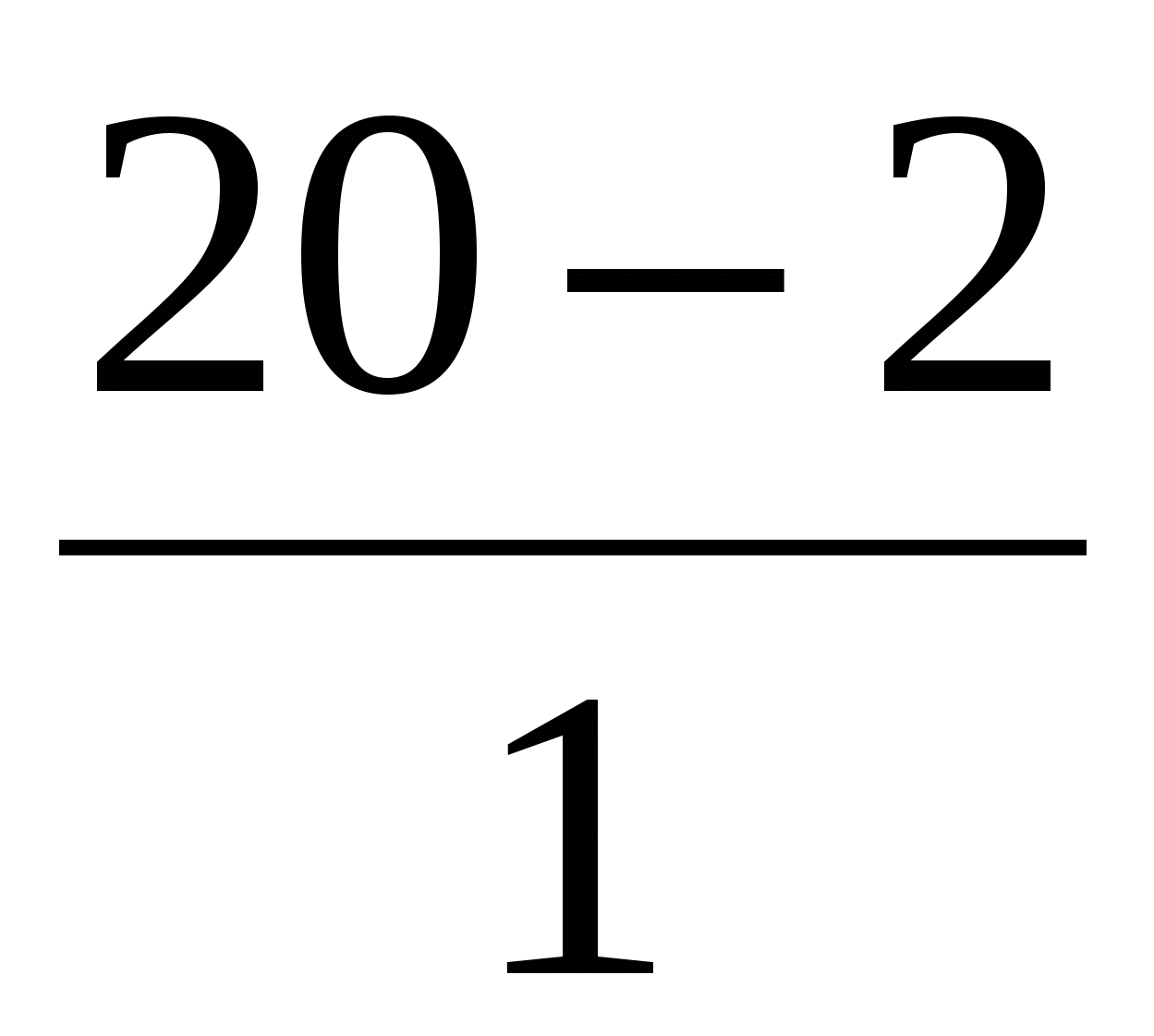 =146 або =146 або
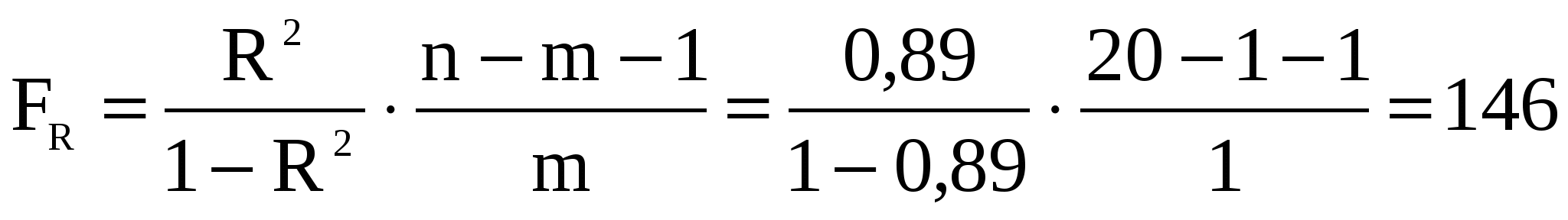 . .
Побудована модель є адекватною, оскільки обчислене за F – критерієм значення більш ніж критичне F(0,05;1;18)=4,41). Це означає також, що коефіцієнт множинної детермінації значущ.
Розрахуємо значення незміщеної оцінки дисперсії залишків у матричному вигляді:
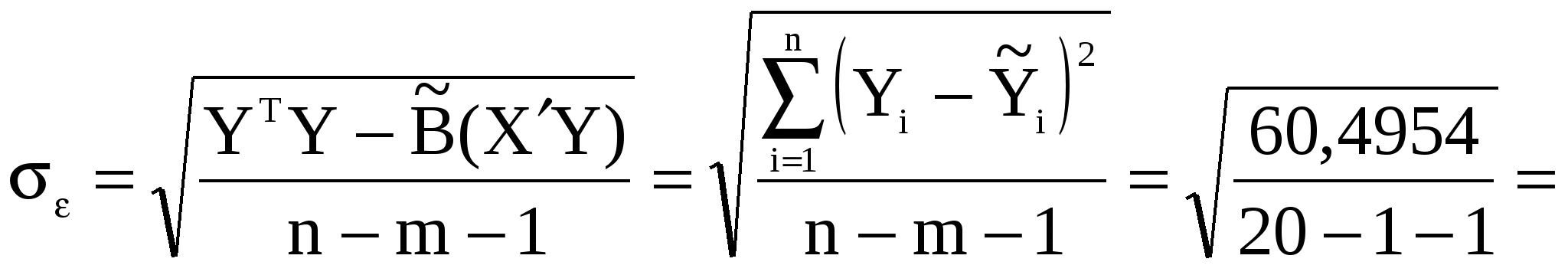 1,833. 1,833.
Обчислимо дисперсійно – коваріаційну матрицю
var(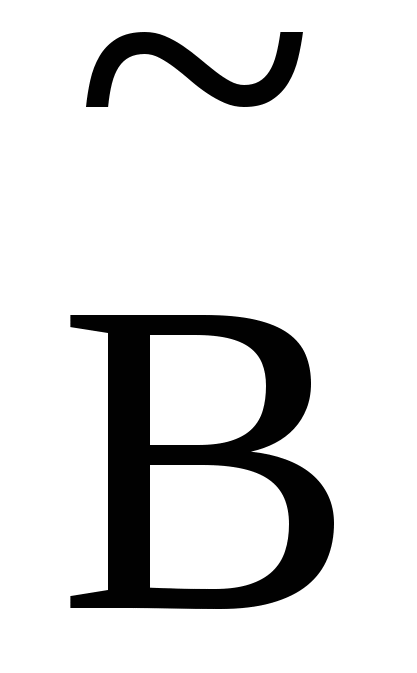 )= )=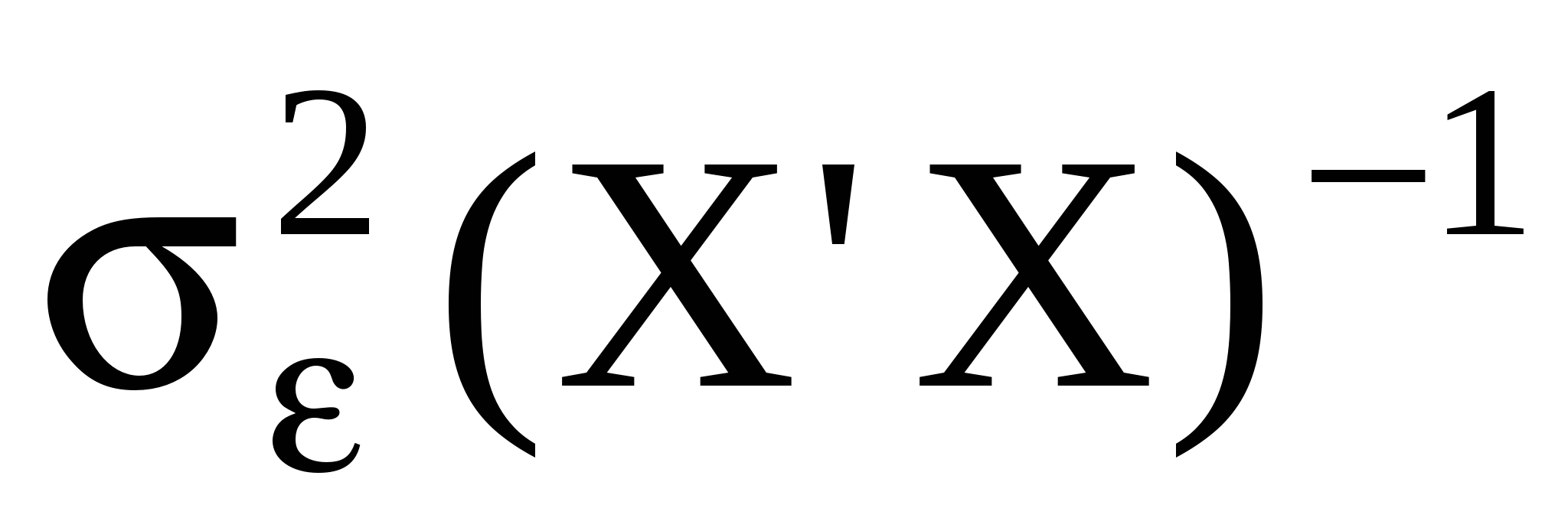 = =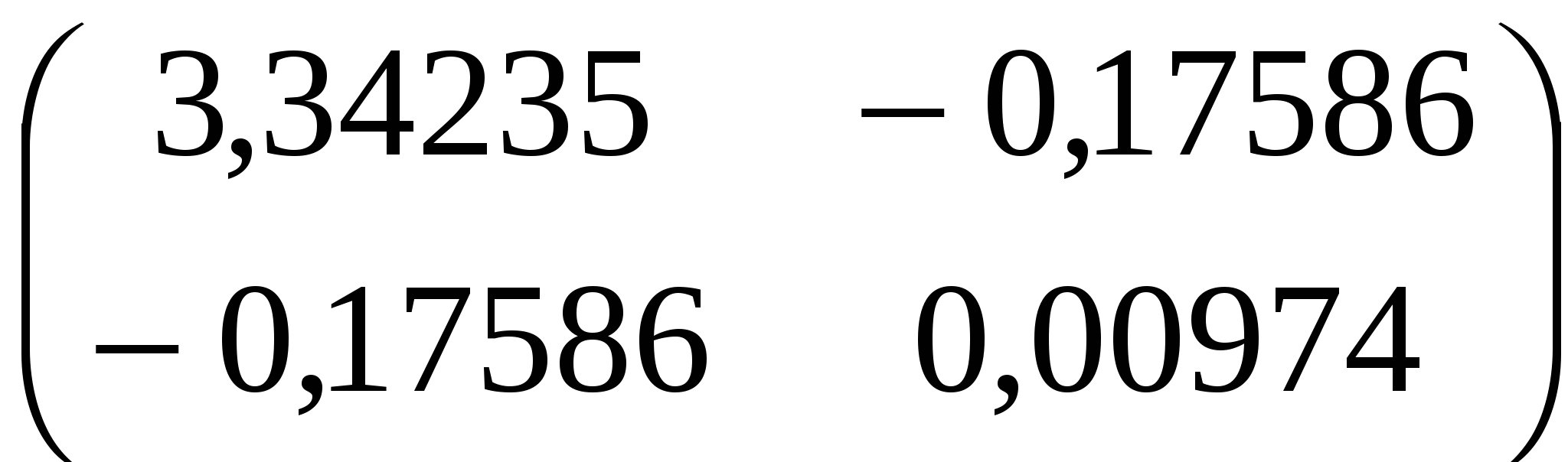 . .
Малюнок 3. 6 Розрахунок дисперсійно-кореляційної матриці
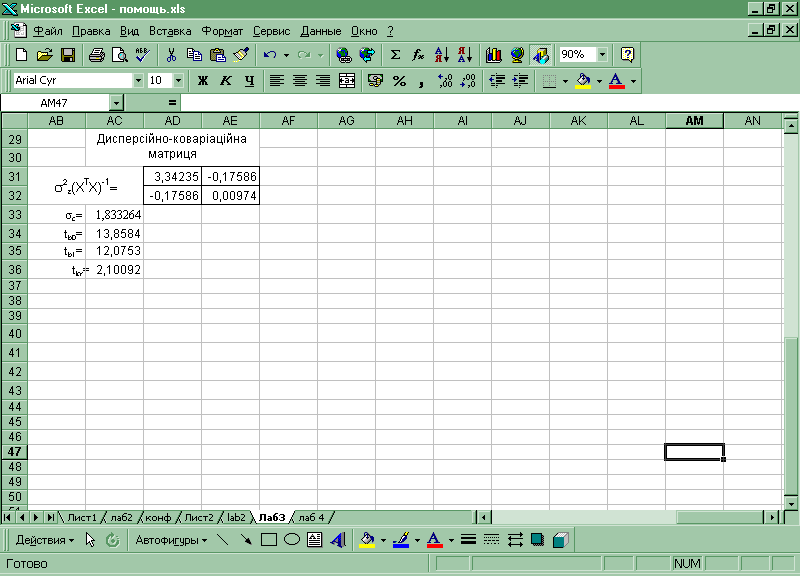
Стандартні помилки оцінок параметрів моделі 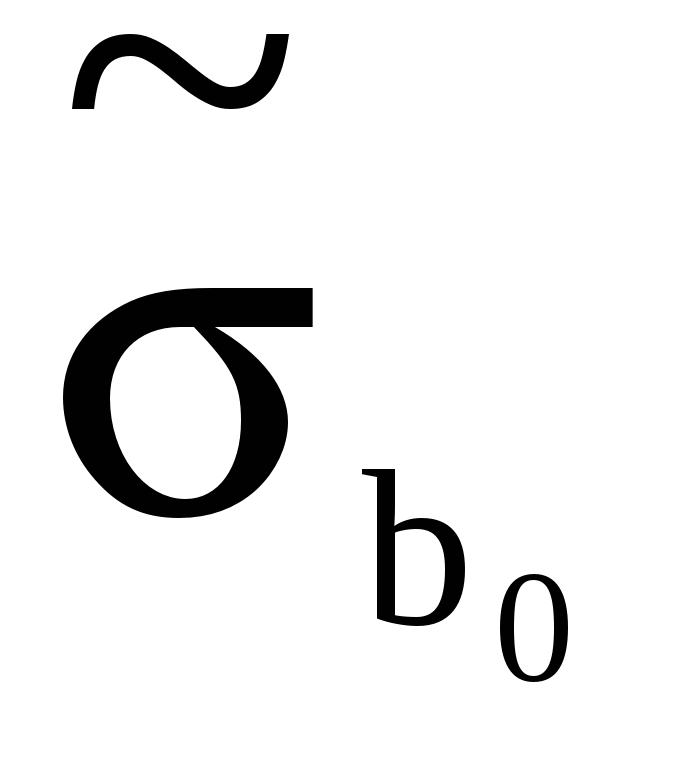 =1,828, =1,828, 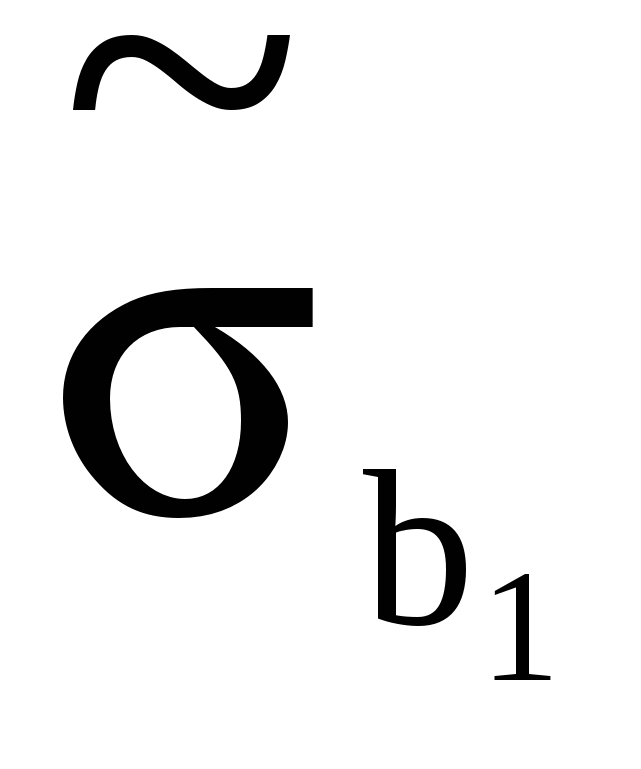 =0,0987, знайдено обчисливши квадратні корні від чисел 3,34235 і 0,00974 відповідно. =0,0987, знайдено обчисливши квадратні корні від чисел 3,34235 і 0,00974 відповідно.
Знайдемо значення t статистики:
tb0=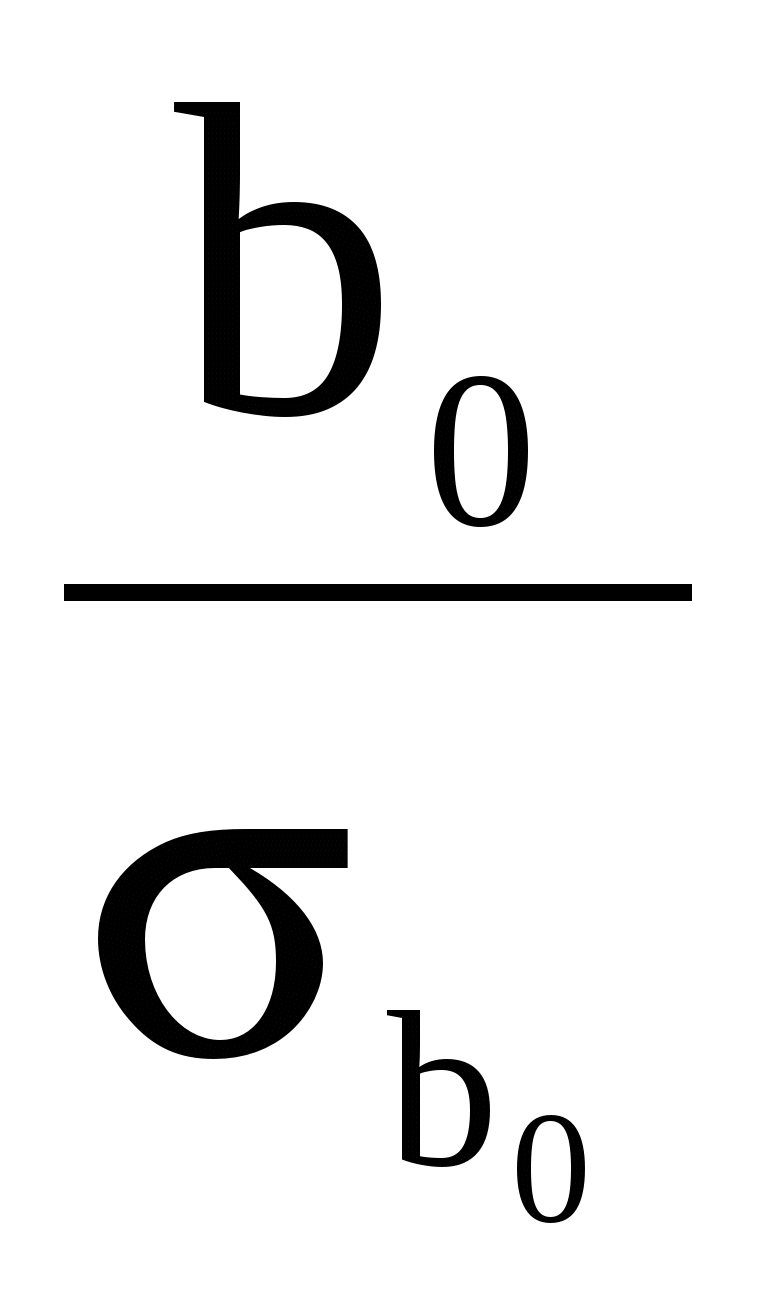 = =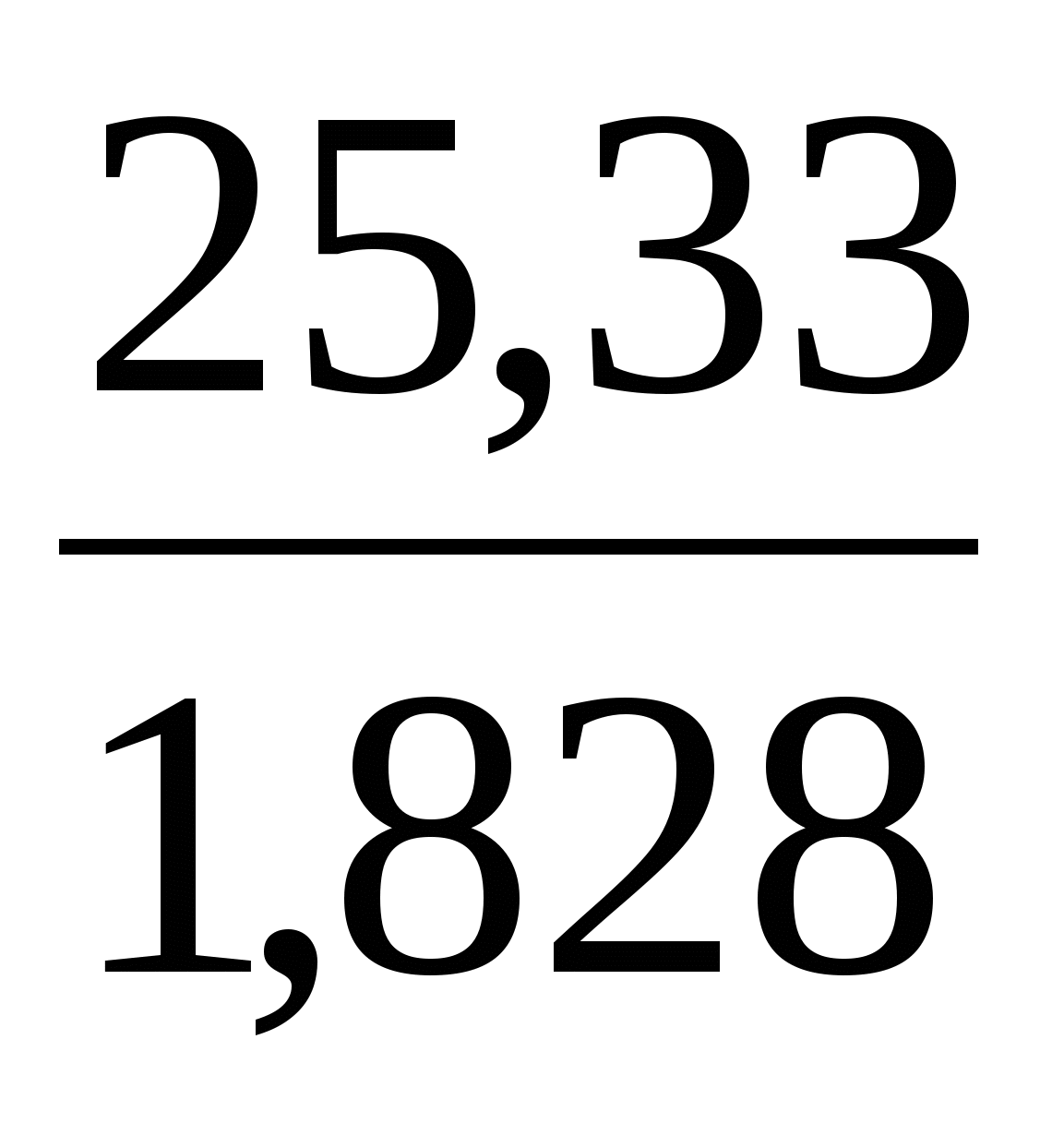 =13,8584, =13,8584, 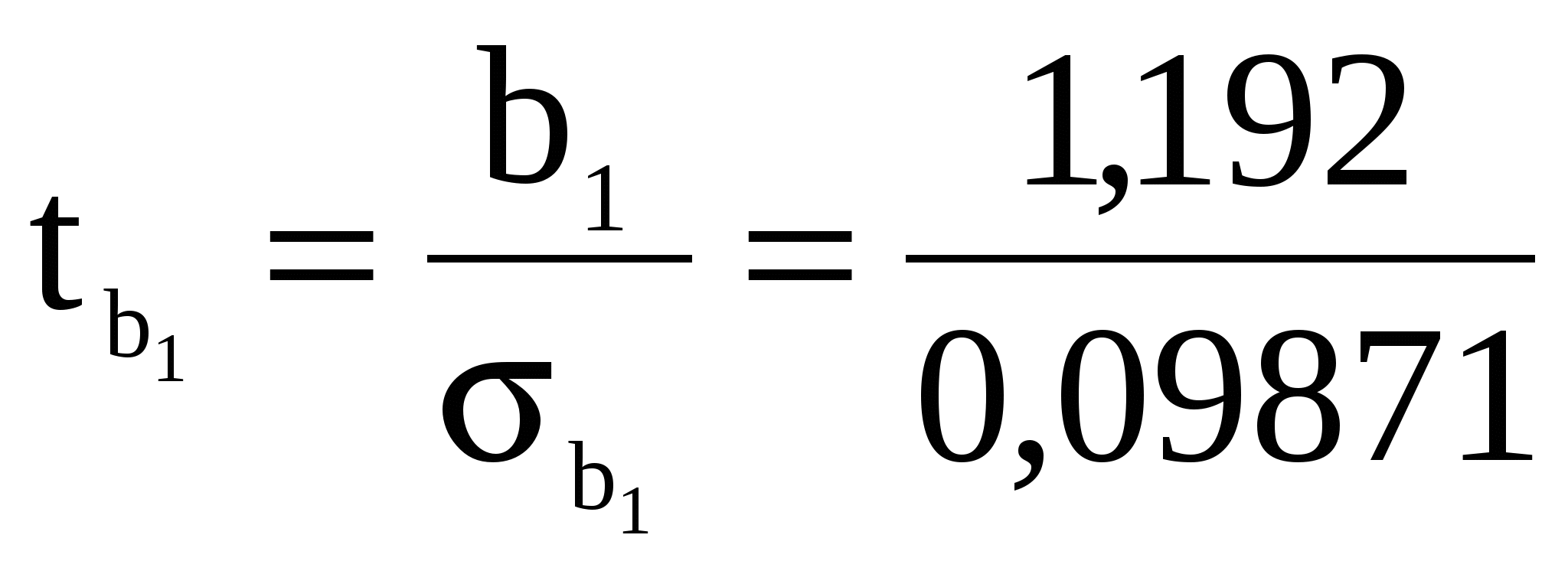 =12,0753, тобто параметри є статистично значущими, оскільки ці значення більш ніж tкр=2,101, яке знайдено при рівні значущості α=0,05 і ступені вільності n-m-1=18, де n – обсяг вибірки, m – кількість незалежних факторів. =12,0753, тобто параметри є статистично значущими, оскільки ці значення більш ніж tкр=2,101, яке знайдено при рівні значущості α=0,05 і ступені вільності n-m-1=18, де n – обсяг вибірки, m – кількість незалежних факторів.
Знайдемо точкове значення прогнозу для 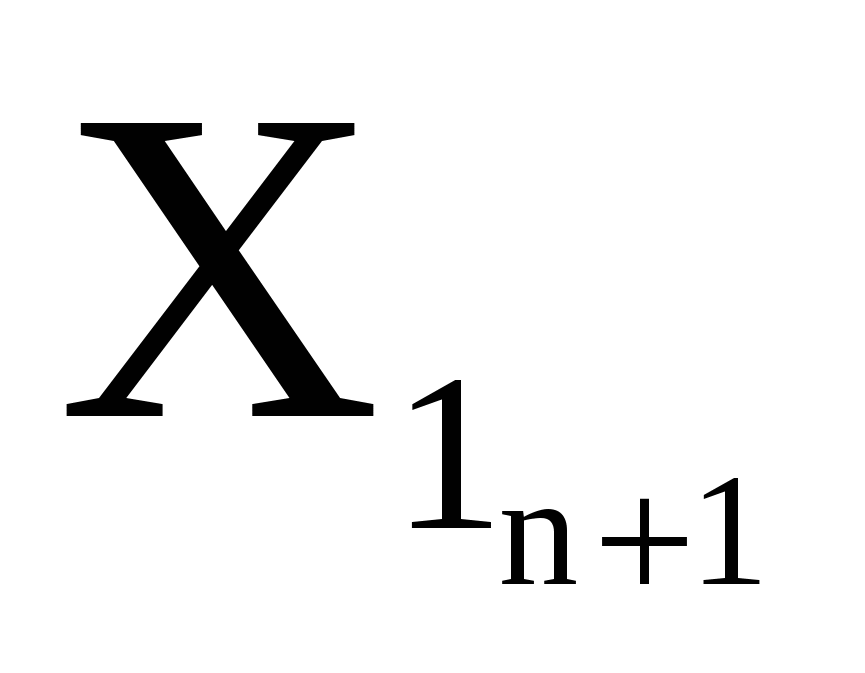 , що дорівнює 19,85, для цього це значення підставимо в рівняння отриманої моделі: , що дорівнює 19,85, для цього це значення підставимо в рівняння отриманої моделі:
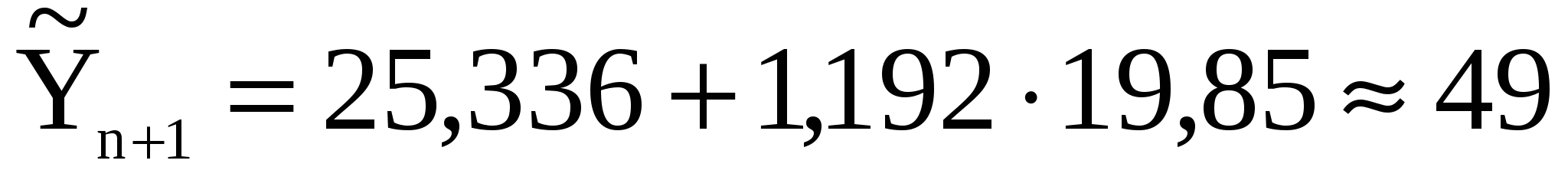 . .
Щоб отримати інтервальний прогноз необхідно розрахувати стандартну помилку прогнозу індивідуального значення:
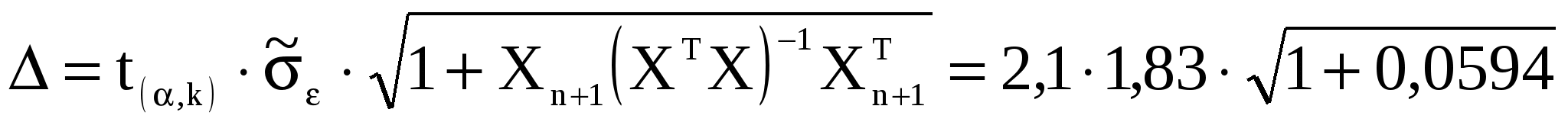 =3,964. =3,964.
Звідси 49–3,964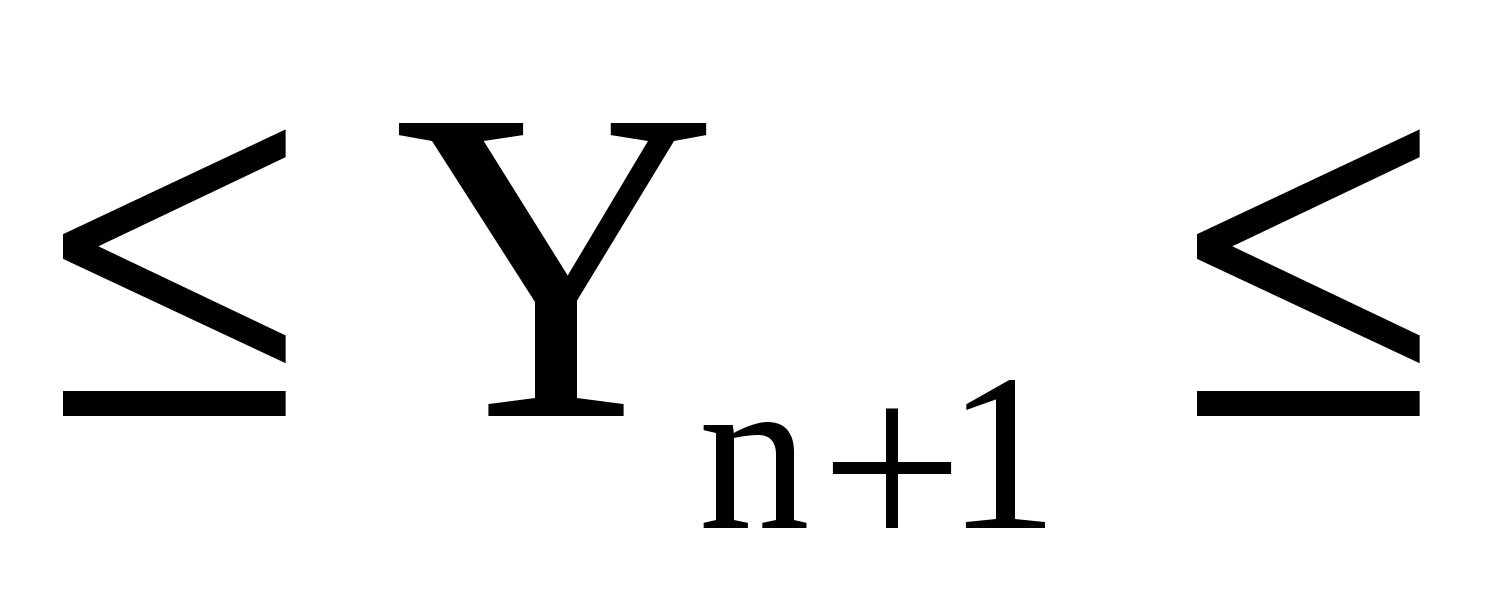 49+3,964, тобто 45,04 49+3,964, тобто 45,04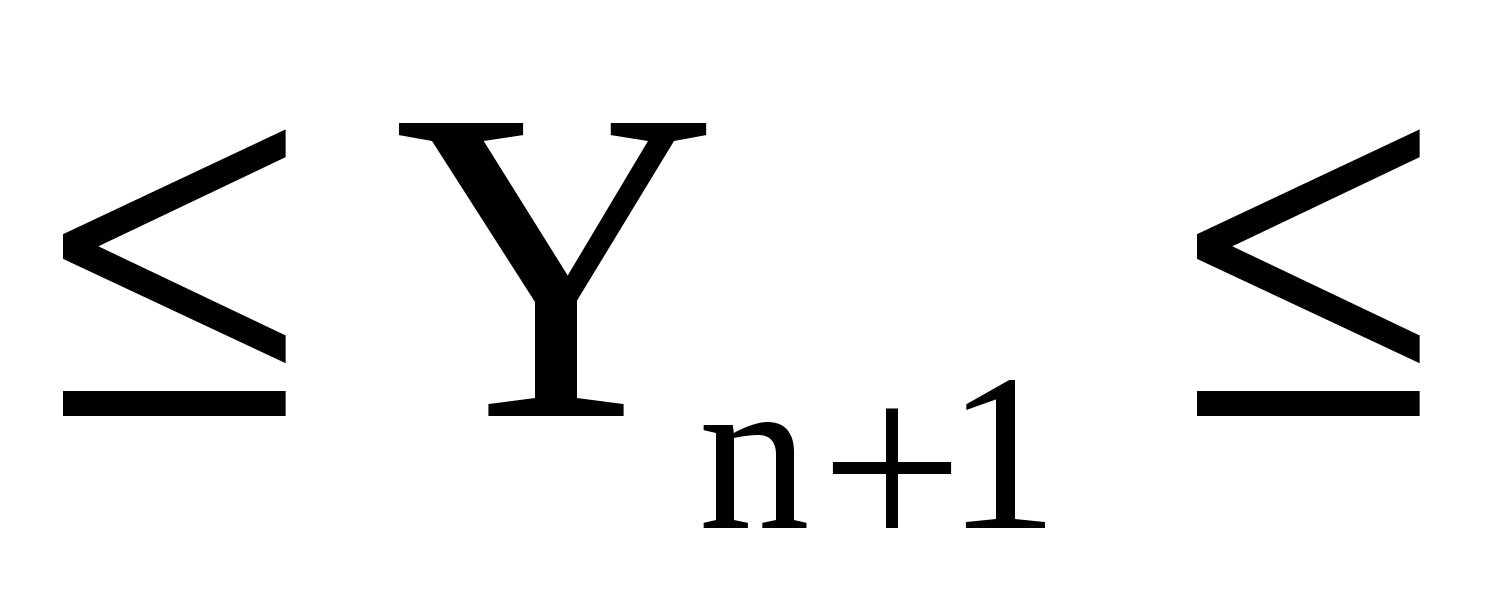 52,96. 52,96.
У нас залишився тільки один незалежний фактор Х1. Значення часткового коефіцієнта еластичності для точки прогнозу знаходиться за формулою:
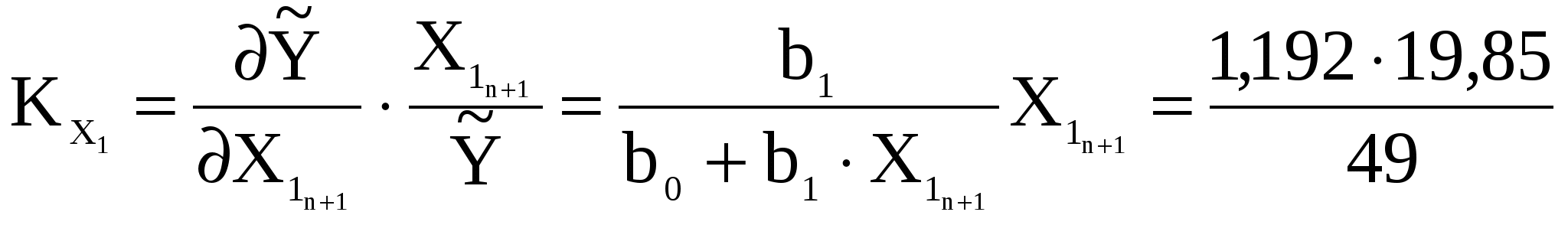 =0,48. =0,48.
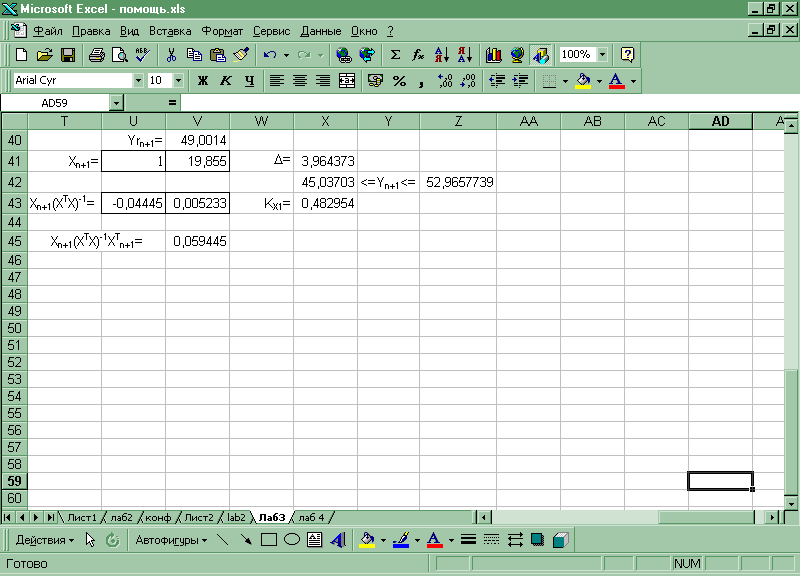
Всі розрахунки в Excel наведені нижче:
Малюнок 3. 7 Розрахунки для точкового і інтервального прогнозного значення тачастковго коефіцієнта еластичності.
ВИСНОВКИ
Використовуючи можливості пакету Excel, була побудована кореляційна матриця:
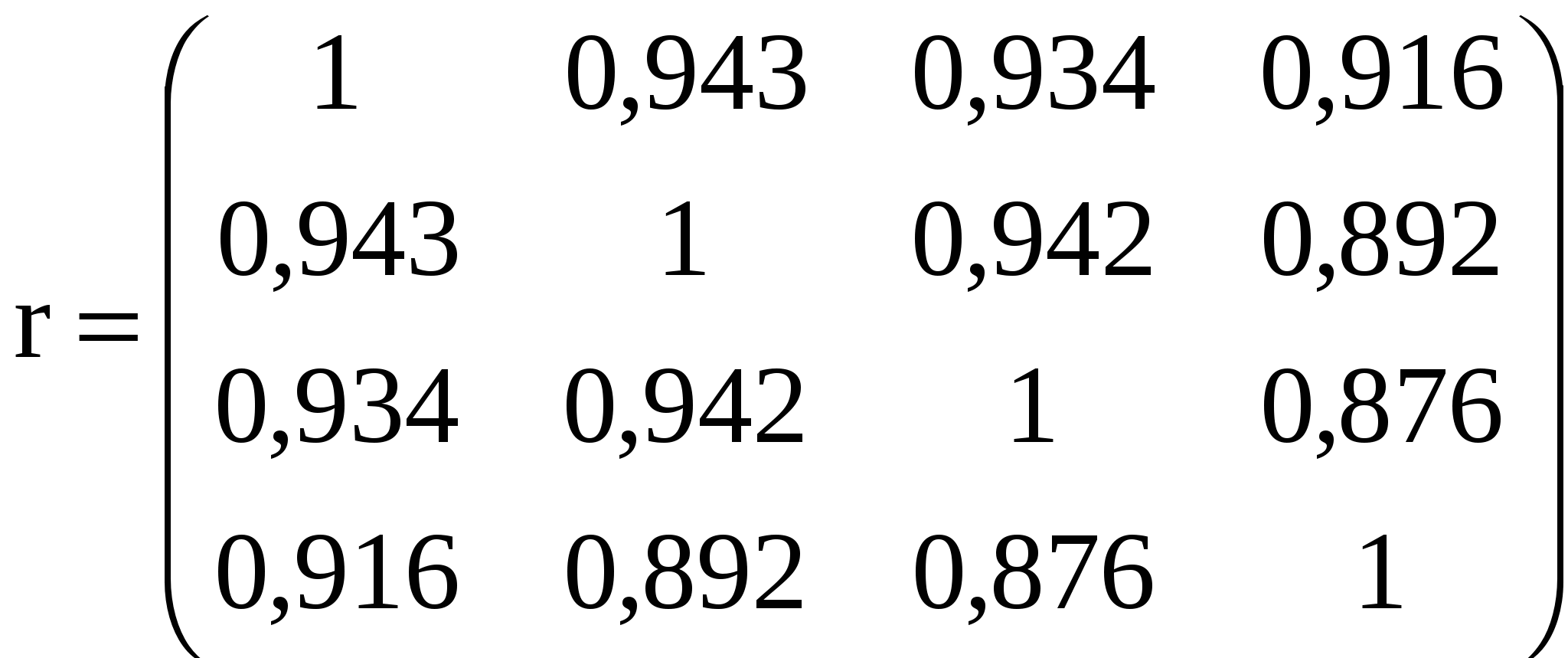 . .
Елементами цієї матриці є парні лінійні коефіцієнти кореляці. Починаючи з другого рядка і другого стовпчика вони попарно характеризують парний лінійний зв’язок між умовно незалежними факторами економетричної моделі Хі. Як видно з цих значень можливо припустити, що в моделі існує таке явище, як мультиколінеарність. Скоріш за все, в моделі залишиться лише один з незалежних факторів. Це підтверджує і розрахунок визначника факторної кореляційної матриці 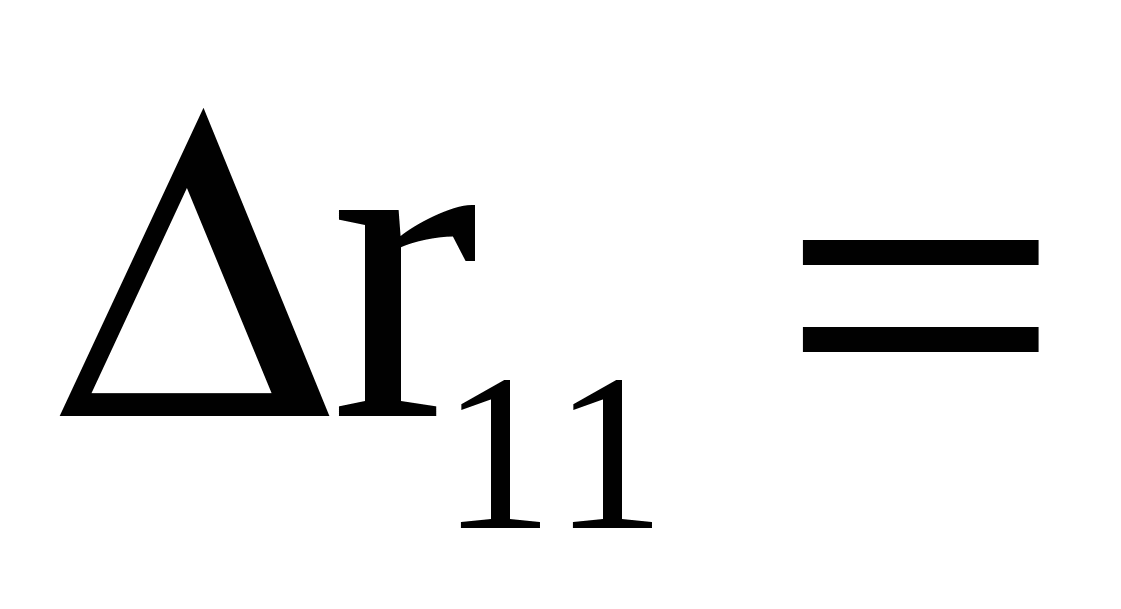 0,02182. Оскільки воно наближується до 0, то в моделі може існувати загальна мультиколінеарність. 0,02182. Оскільки воно наближується до 0, то в моделі може існувати загальна мультиколінеарність.
В результаті розрахунків і перевірки моделі на мультиколінеарність було виявлено, що між факторами Х1 і Х2, а потім і Х1 і Х3 існує залежність, тому на основі аналізу розрахунків в моделі залишився лише один фактор Х1.
Економетрична модель прибутка на місяць має вигляд:
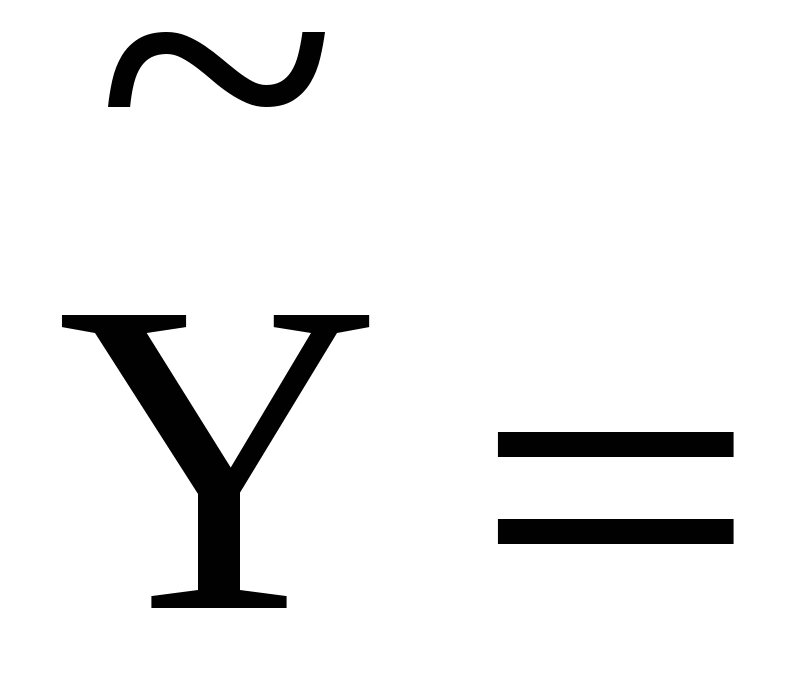 25,336+1,192X1. 25,336+1,192X1.
Зауваження: Коефіцієнти регресії при і-му факторі показують, як буде змінюватись результат, при зміні відповідного фактора на 1 при умові, що інші фактори незмінні.
Коефіцієнт множинної детермінації:
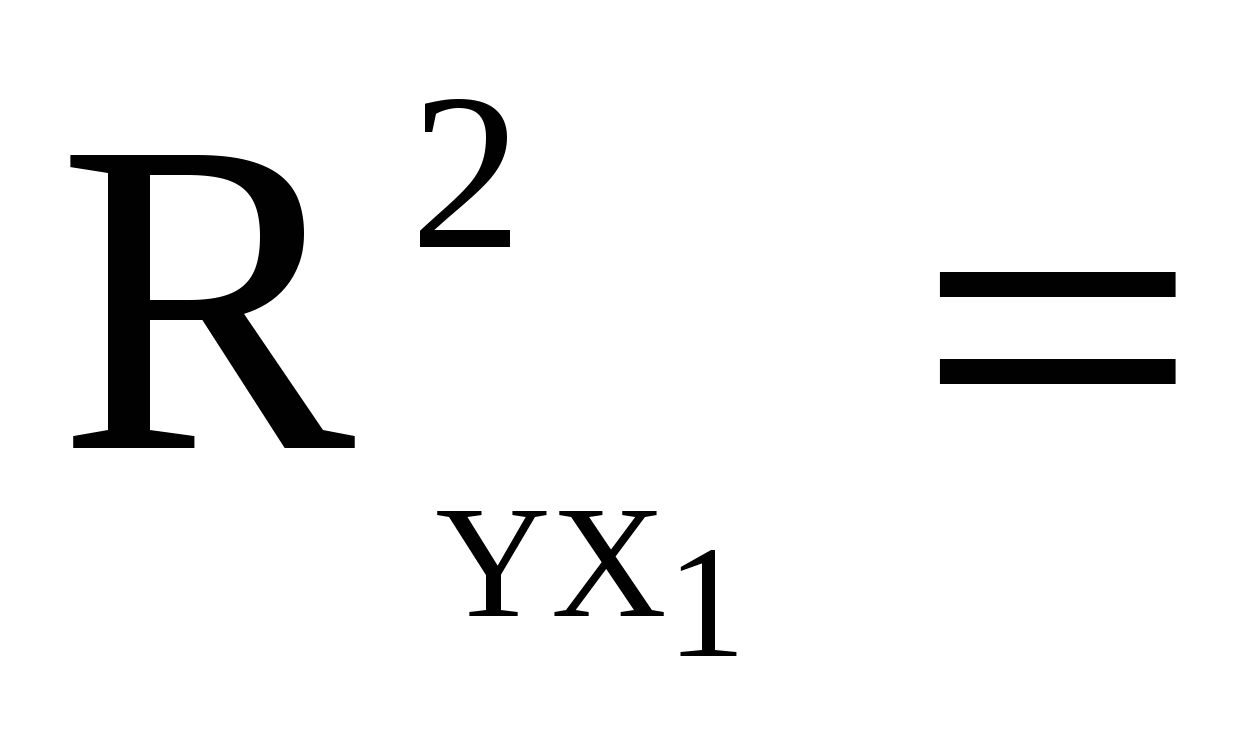 0,89. 0,89.
Він показує, що прибуток на місяць Y на 89% визначається досліджуваними чинниками (для задачи, що розглядалась фондовіддачею Х1).
Множиний коефіцієнт кореляції 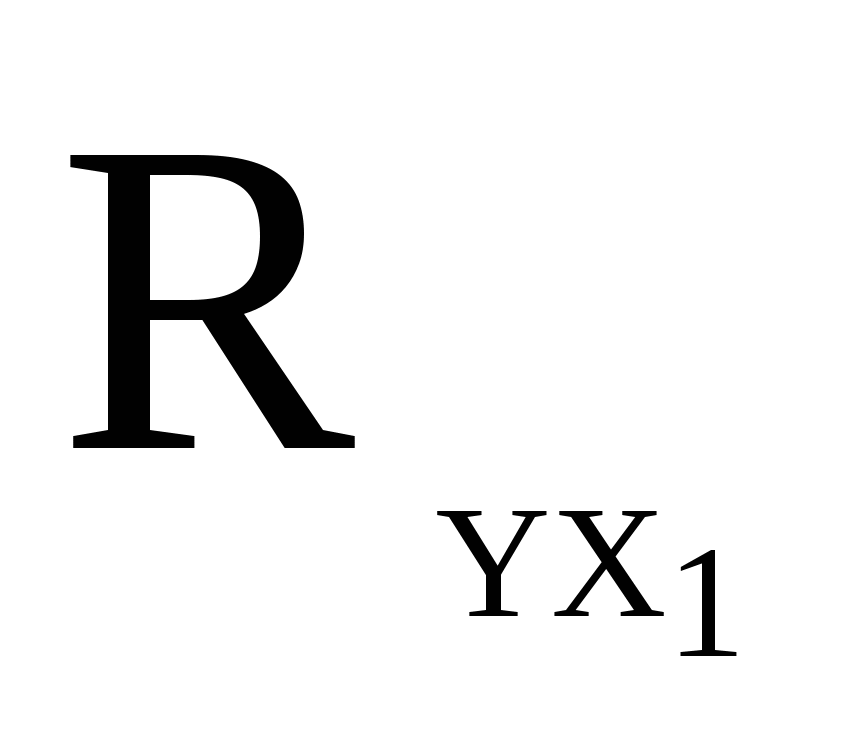 =0,943 На підставі цього коефіцієнта можна стверджувати, що зв’язок між прибутком та досліджуваними чинникам – тісний. =0,943 На підставі цього коефіцієнта можна стверджувати, що зв’язок між прибутком та досліджуваними чинникам – тісний.
Критерій Фішера 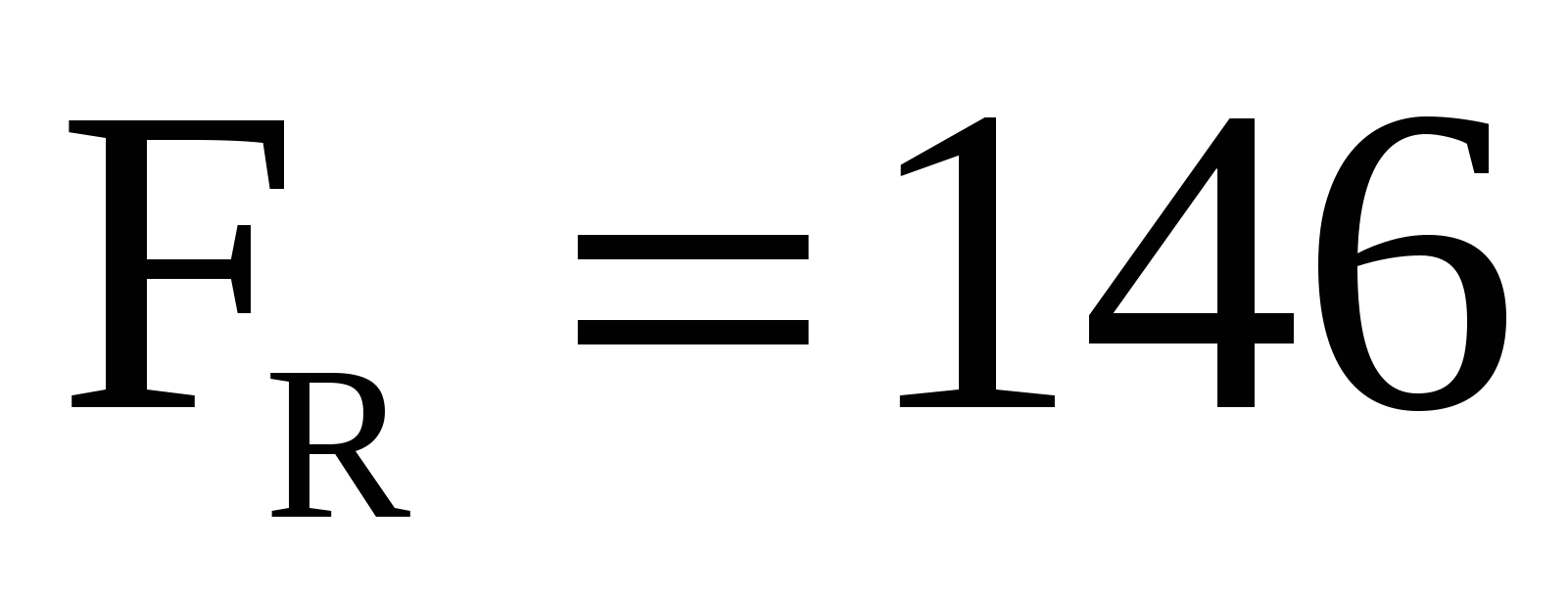 . Табличне (критичне) його значення за рівня значущості α=0,05, ступенів вільності k1=1 і k2=18 дорівнює F(0,05;1;18)=4,41. Оскільки розрахункове значення цього критерію більш ніж табличне, то з надійністю 0,95 можна зробити висновок про адекватність побудованої моделі, а також про підтведження гіпотези про статистичну значущість зв’язку на основі економетричної моделі. . Табличне (критичне) його значення за рівня значущості α=0,05, ступенів вільності k1=1 і k2=18 дорівнює F(0,05;1;18)=4,41. Оскільки розрахункове значення цього критерію більш ніж табличне, то з надійністю 0,95 можна зробити висновок про адекватність побудованої моделі, а також про підтведження гіпотези про статистичну значущість зв’язку на основі економетричної моделі.
Перевірка достовірності кожної оцінки параметрів моделі на основі t – критерію показала, що кожна з оцінок отриманих параметрів b0 і b1 є статистично значущими з надійністю 0,95. Таким чином, достовірность моделі в цілому досягається за рахунок параметрів b0 і b1.
Зауваження. При перевірці значимості оцінок параметрів моделі інколи виникає ситуація, коли не всі оцінки параметрів є статистично значущими. Наприклад, в економетричній моделі залишилось чотири фактора і тільки для останніх трьох оцінки параметрів виявились статистично значущими, тоді роблять висновок, що достовірність моделі в цілому досягається за рахунок останніх трьох параметрів.
Точковий та інтервальний прогнози згідно з отриманою економетричною моделлю:
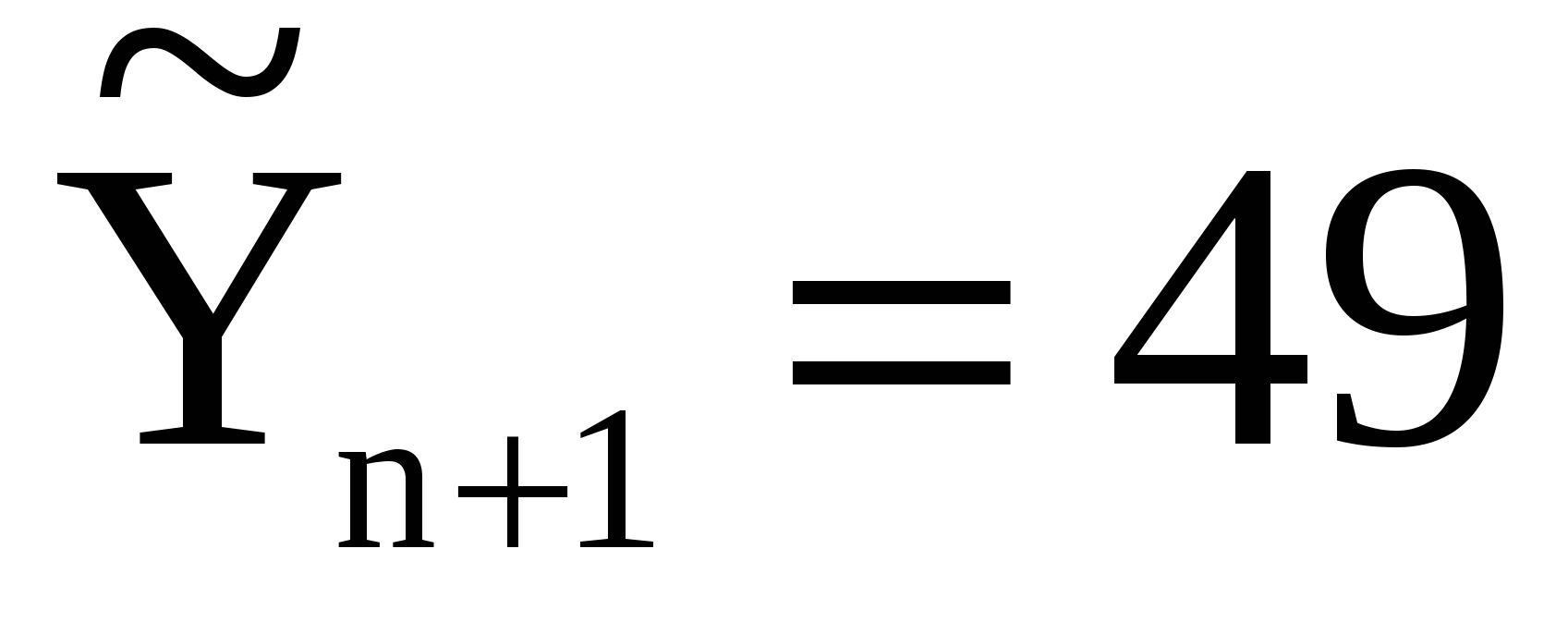 і 45,04 і 45,04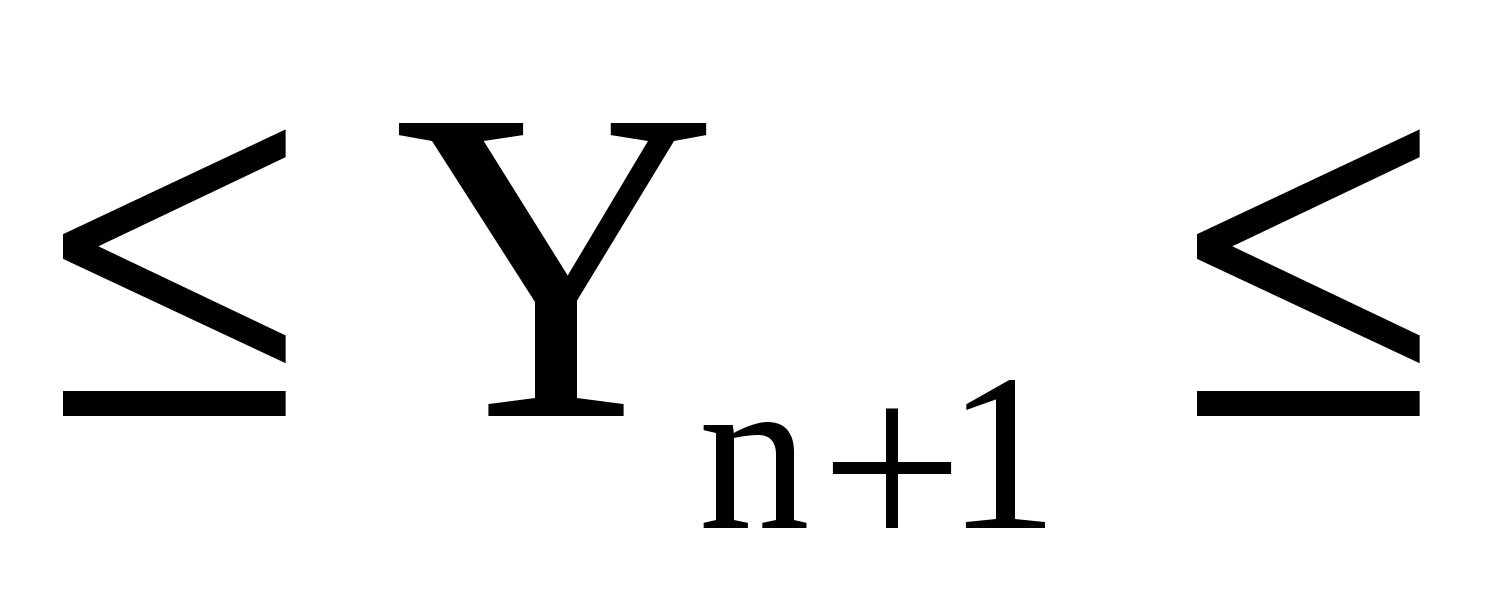 52,96. 52,96.
Частковий коефіцієнт еластичності показує на скільки відсотків зміниться показник, якщо один із факторів зміниться на один відсоток при умові, що інші фактори не змінюються. Еластичність першого чинника для точки прогнозу показала, що при зростанні фондоввідачі на 1% прибуток збільшиться на 0,48%.
Зауваження. Якщо модель буде мати декілька чинників, то в цьому випадку аналізуючи еластичність чинника необхідно робити наступний висновок, що при зростанні певного чинника на 1% і незміні інших, результат збільшиться на стільки-то відсотків.
Додаток 3. 1 Розрахунки в Excel
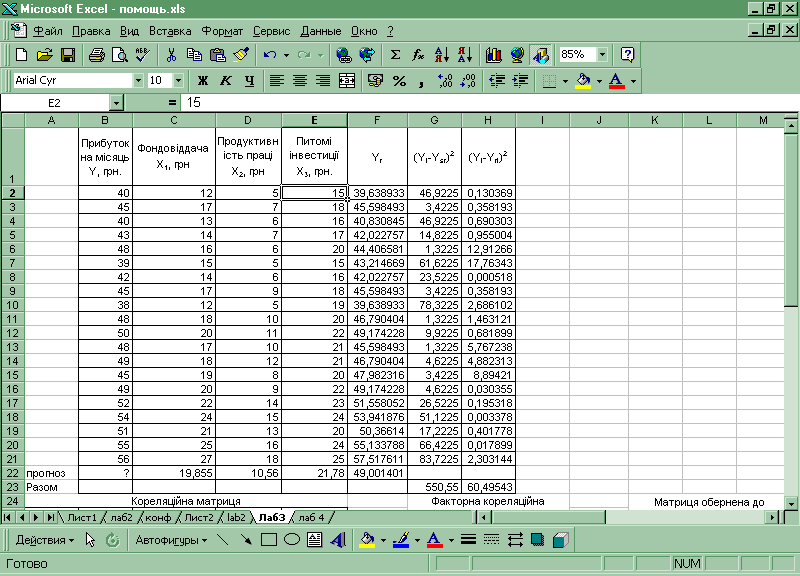
Додаток 3. 2 Розрахунки в Excel
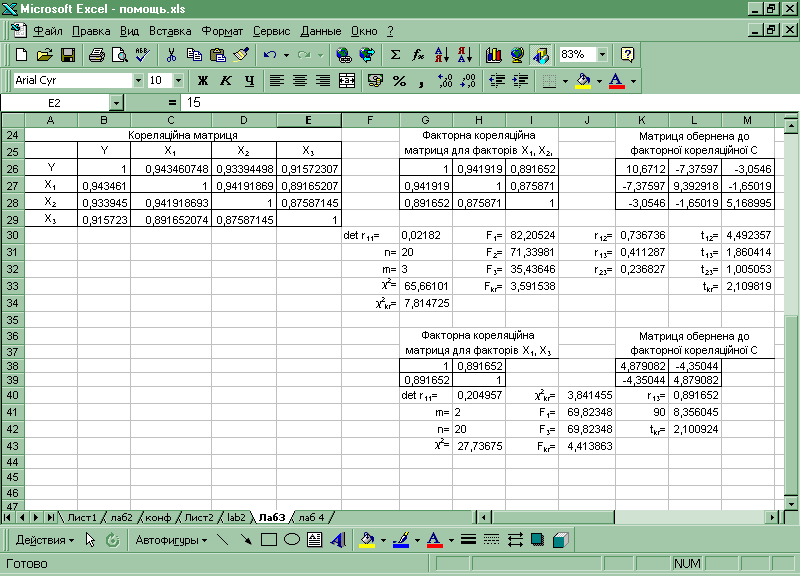
Додаток 3. 3 Розрахунки в Excel
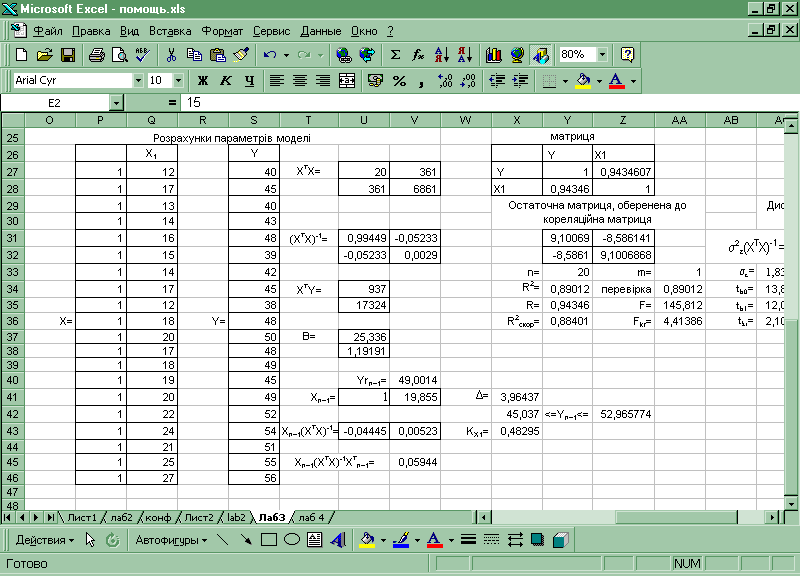
Додаток 3. 4 Розрахунки в Excel
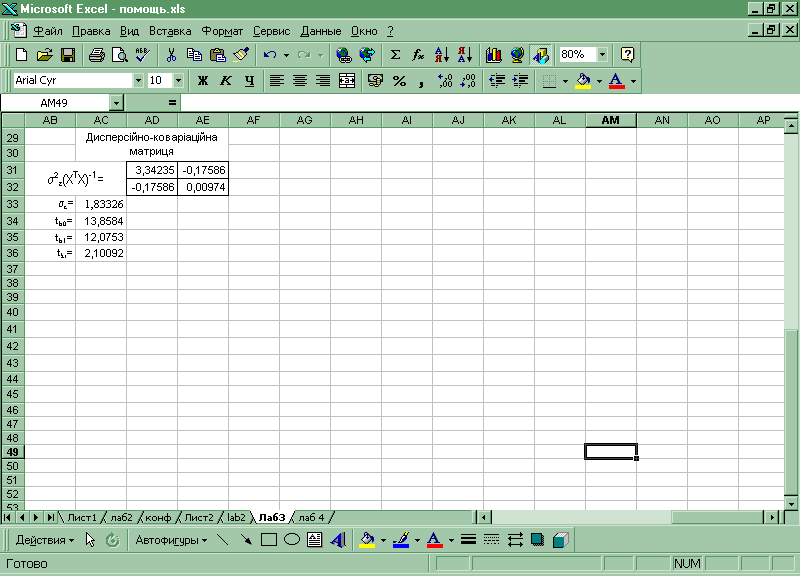
АМСУ кафедра статистики Лавренюк І.В.
|
 Скачать 456.5 Kb.
Скачать 456.5 Kb. ,
,

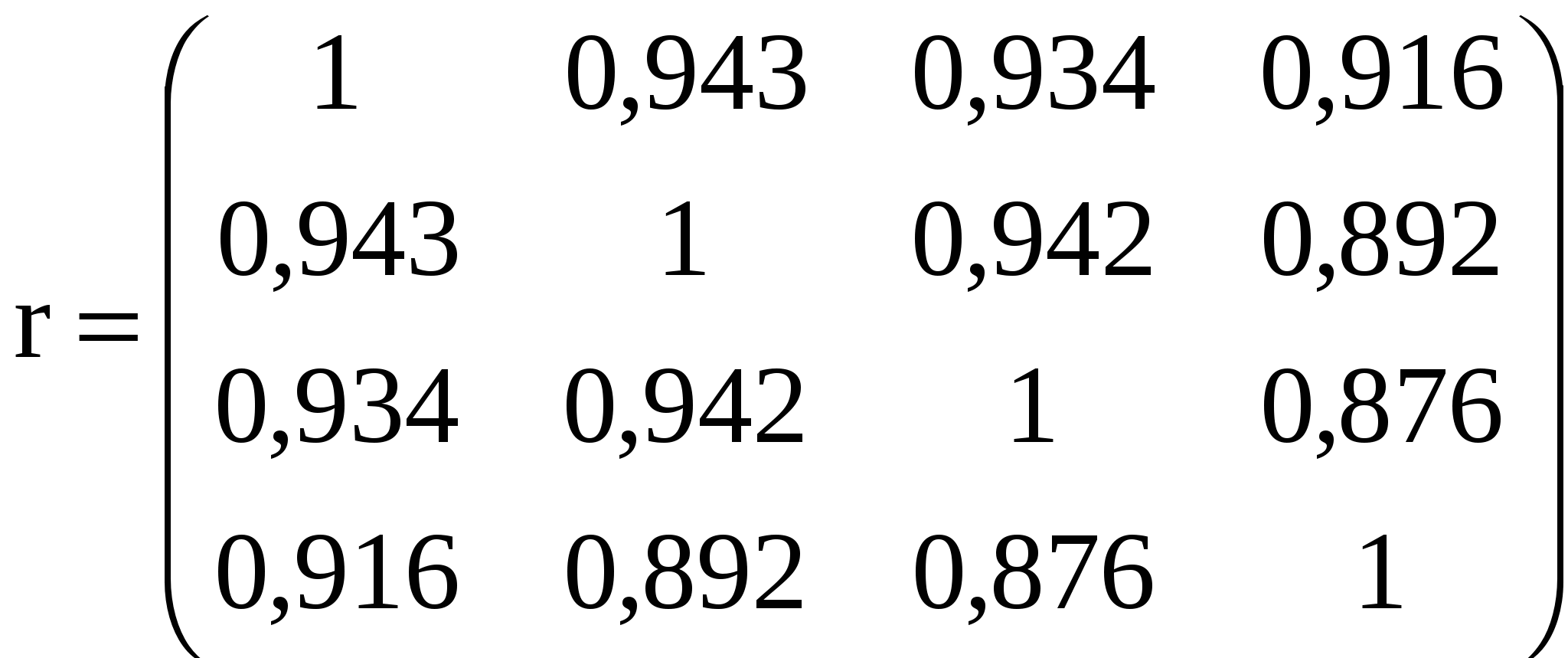 .
.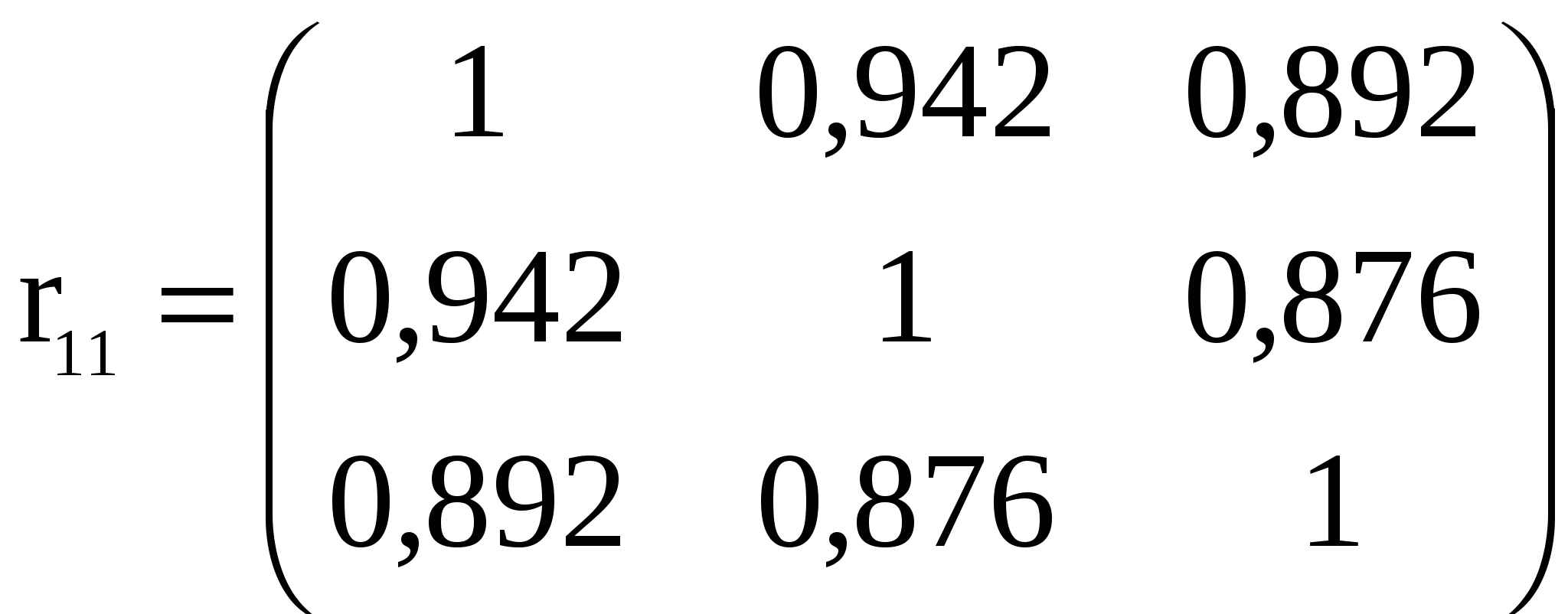 .
.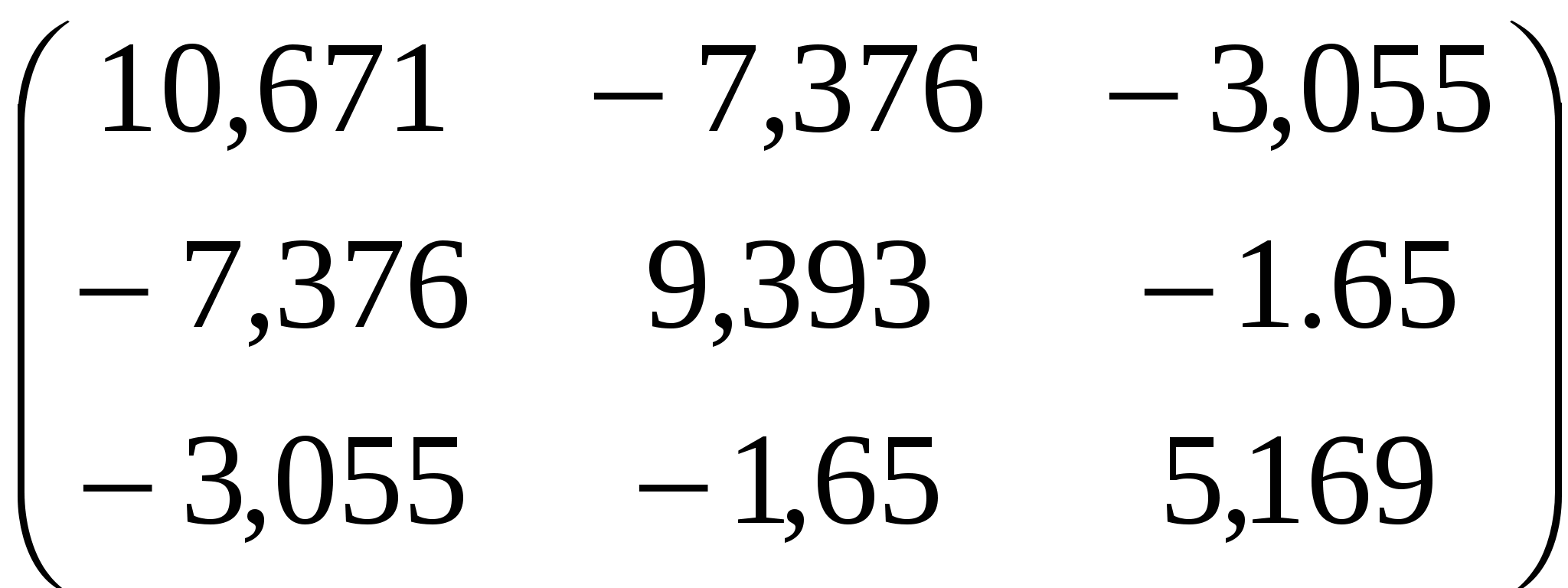 .
.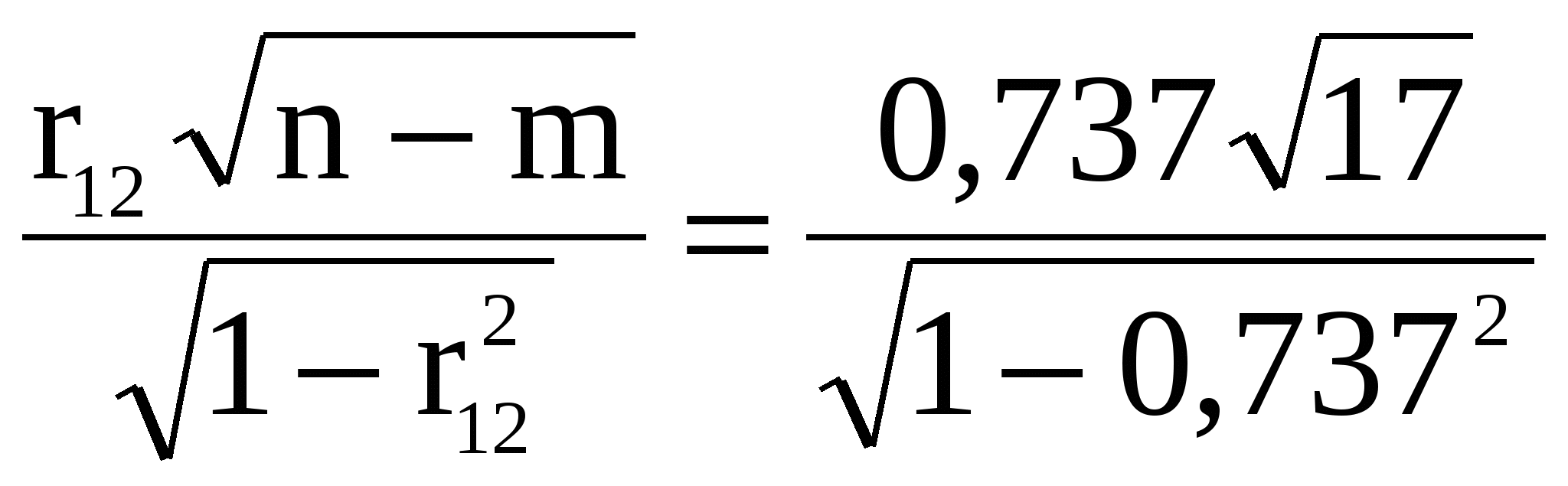 =4,49;
=4,49;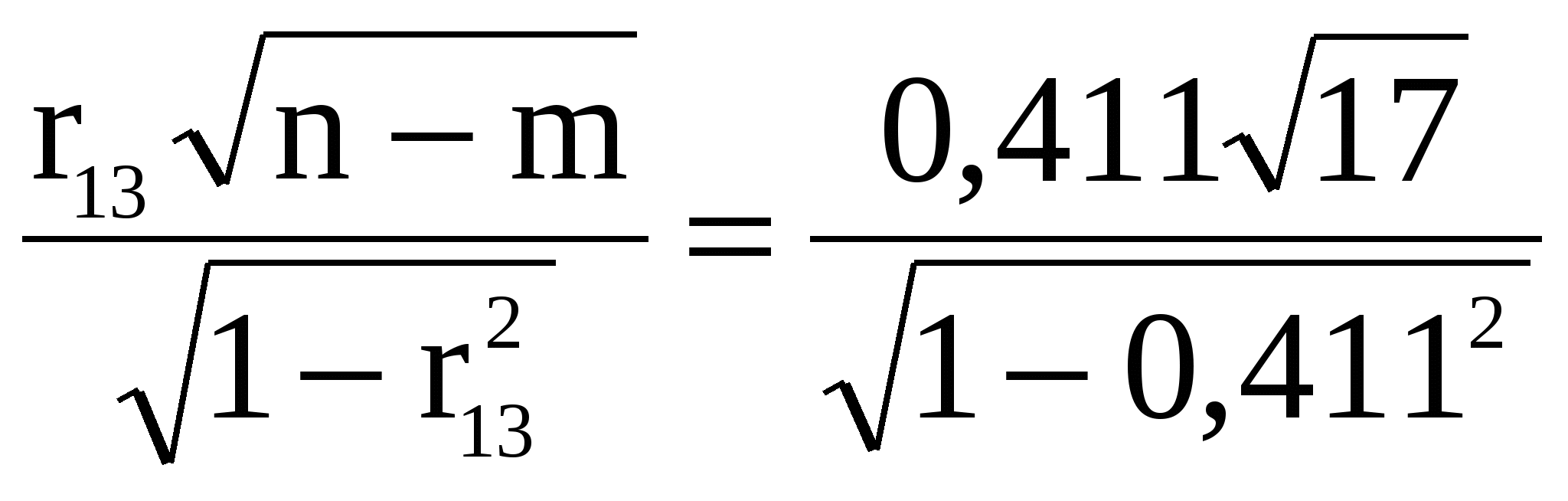 =1,86;
=1,86;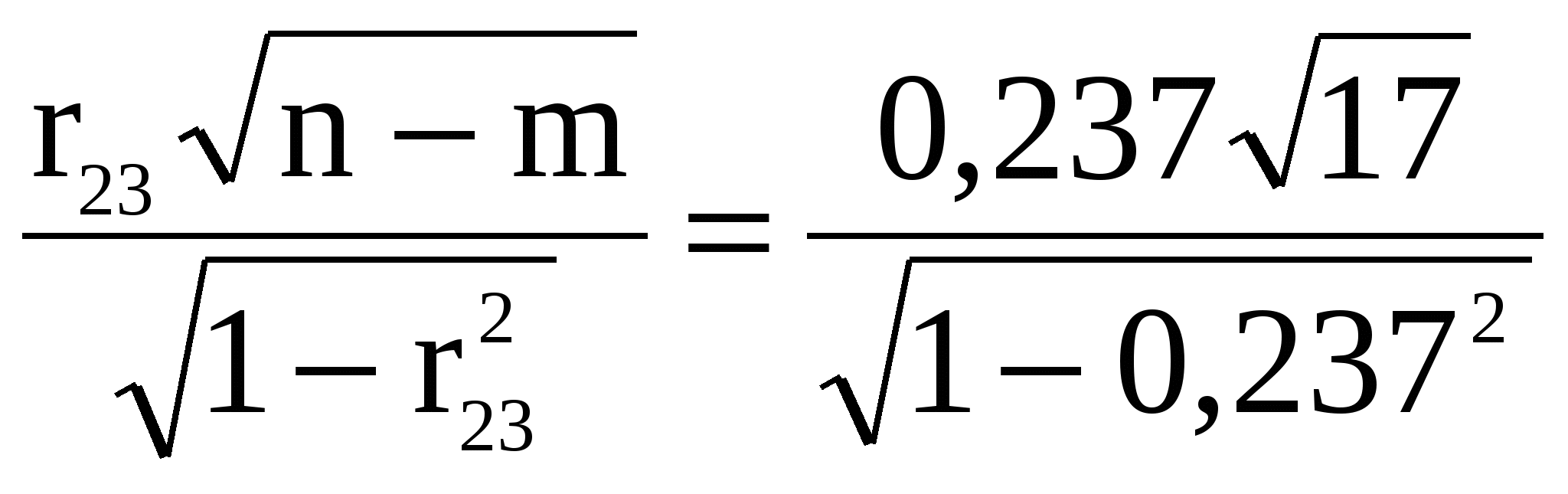 =1,005.
=1,005.


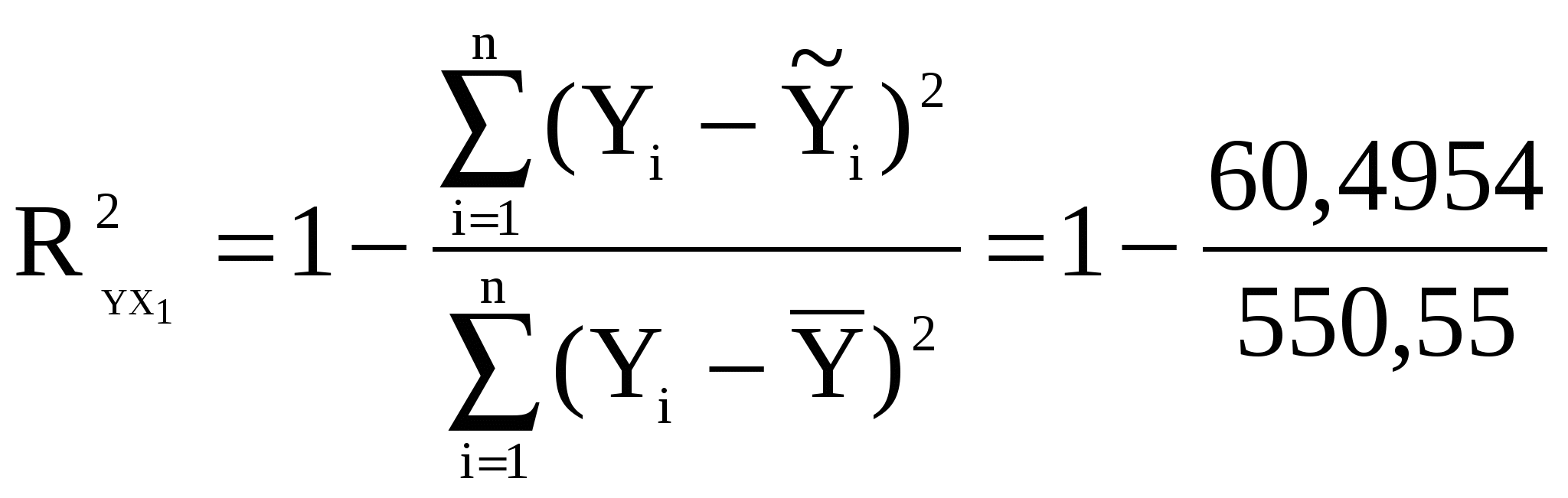 =0,89.
=0,89.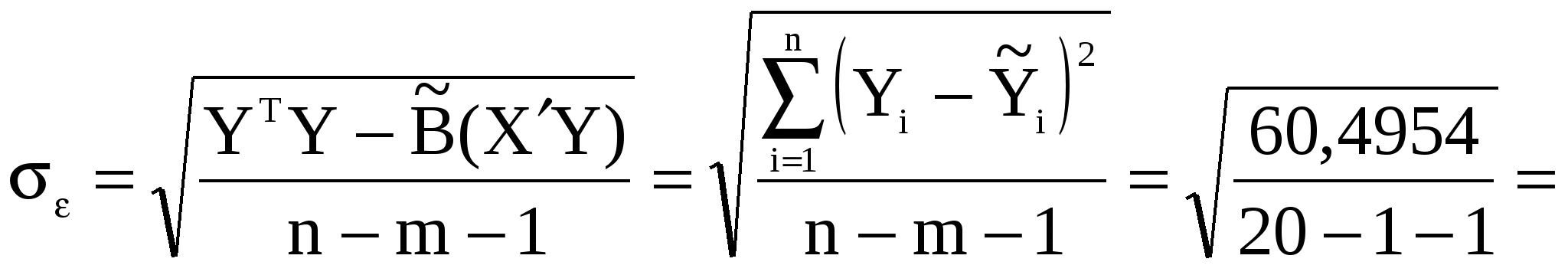 1,833.
1,833.
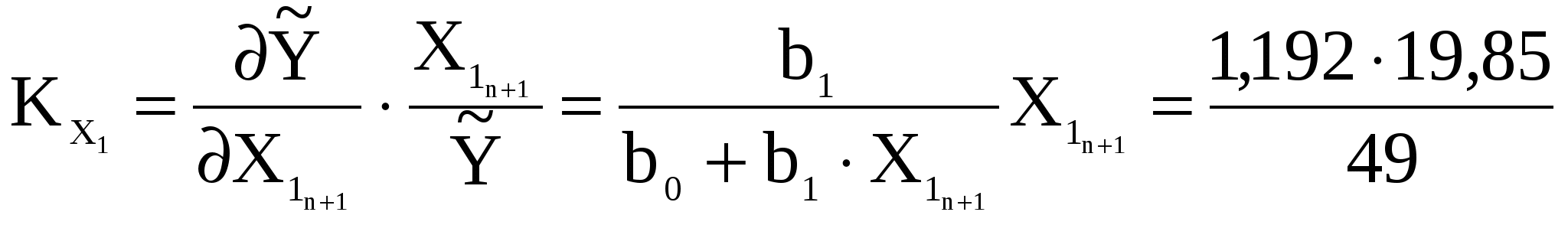 =0,48.
=0,48.
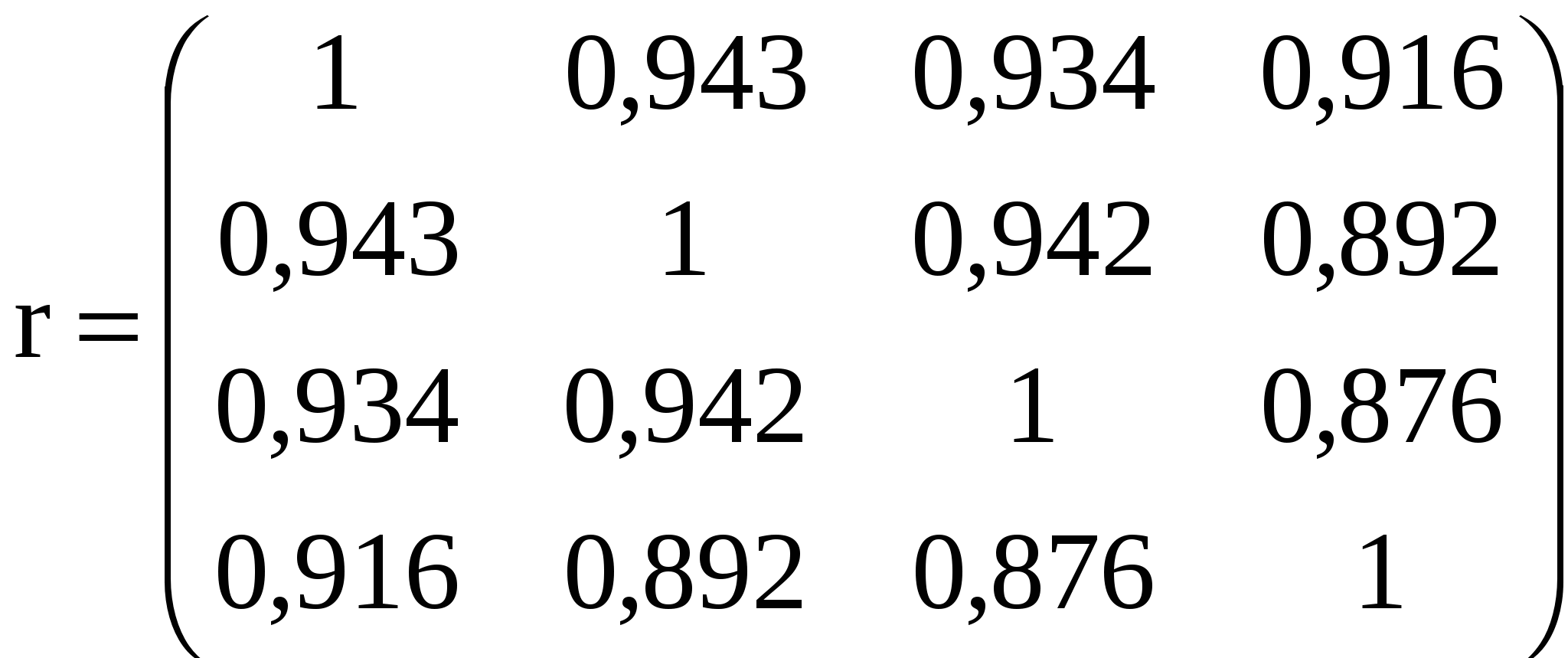 .
.



