ЛР4 Дифракційна ґратка. Лабораторна робота 4 вивчення явища дифракції світла. Визначення сталої дифракційної ратки з використанням екрана з міліметровою шкалою

• Название: Лабораторна робота 4 вивчення явища дифракції світла. Визначення сталої дифракційної ратки з використанням екрана з міліметровою шкалою
• Дата: 12.03.2023
• Размер: 281.78 Kb.
• Имя файла: ЛР4 Дифракційна ґратка.docx
• Тип: Лабораторна робота; #983845

ЛАБОРАТОРНА РОБОТА №4

ВИВЧЕННЯ ЯВИЩА ДИФРАКЦІЇ СВІТЛА. ВИЗНАЧЕННЯ СТАЛОЇ ДИФРАКЦІЙНОЇ ҐРАТКИ З ВИКОРИСТАННЯМ ЕКРАНА З МІЛІМЕТРОВОЮ ШКАЛОЮ.

Мета роботи. Визначити сталу дифракційної ґратки та її роздільну здатність.

Прилади і обладнання

1. Дифракційна ґратка.

2. Лазер.

3. Екран з міліметровою шкалою.

Самостійна підготовка.

1. Студент вивчає теорію інтерференції Френеля і Фраунгофера.

2. Вивчає теорію дифракційної ґратки .

3. Вивчає теорію лазерів і характеристики лазерного випромінювання.

4. Вивчає теорію і методику проведення експерименту.
Завдання 1. Визначити сталу дифракційної ґратки.

Для проведення обчислень записати довжину хвилі лазерного випромінювання λ = 632,8 нм.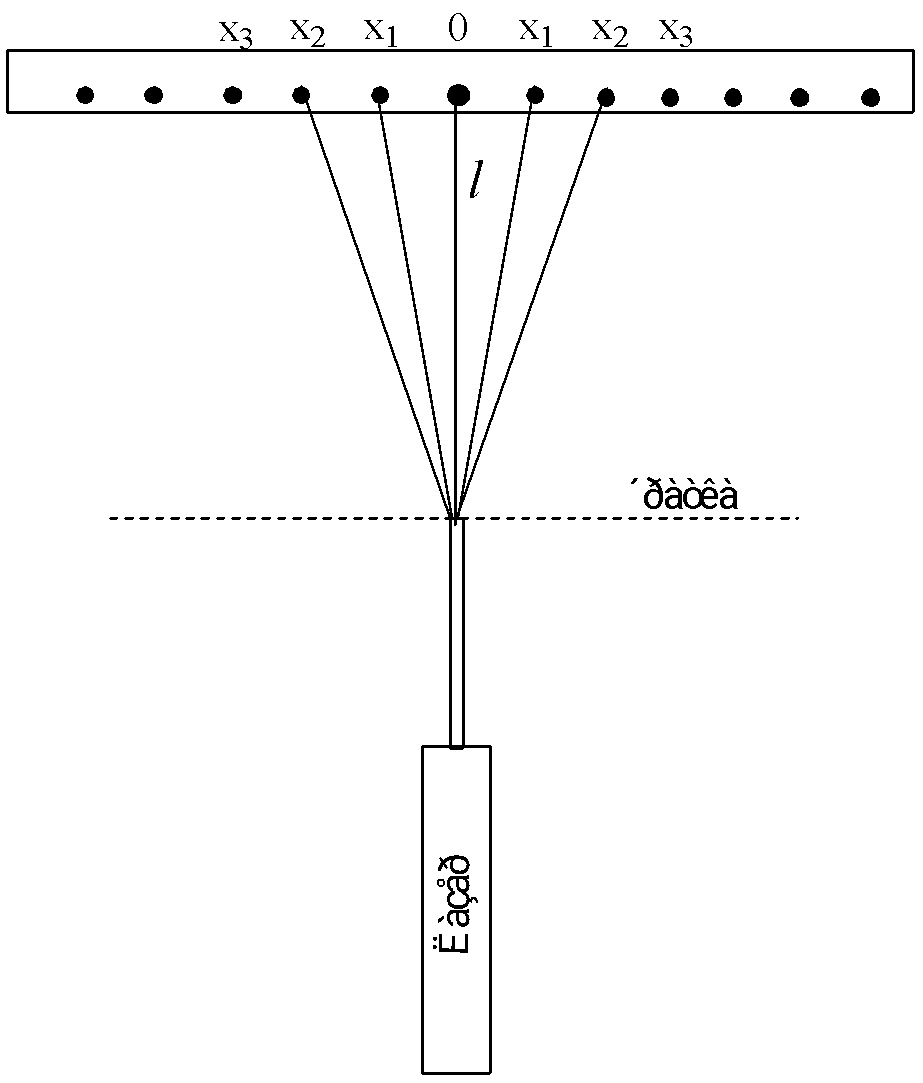

1. Виміряти правий і лівий відліки за міліметровою шкалою.

2. 
   Обчислити відстань між максимумами X_k. Результати занести до табл. 1.
   
3. 
   Розрахувати величину сталої дифракційної ґратки d_i
   

_,

Результати занести до табл. 1.

1.4. Знайти середнє значення сталої дифракційної ґратки d_сер, середнє квадратичне відхилення Δd та відносну похибку ε. Результати занести до табл. 1.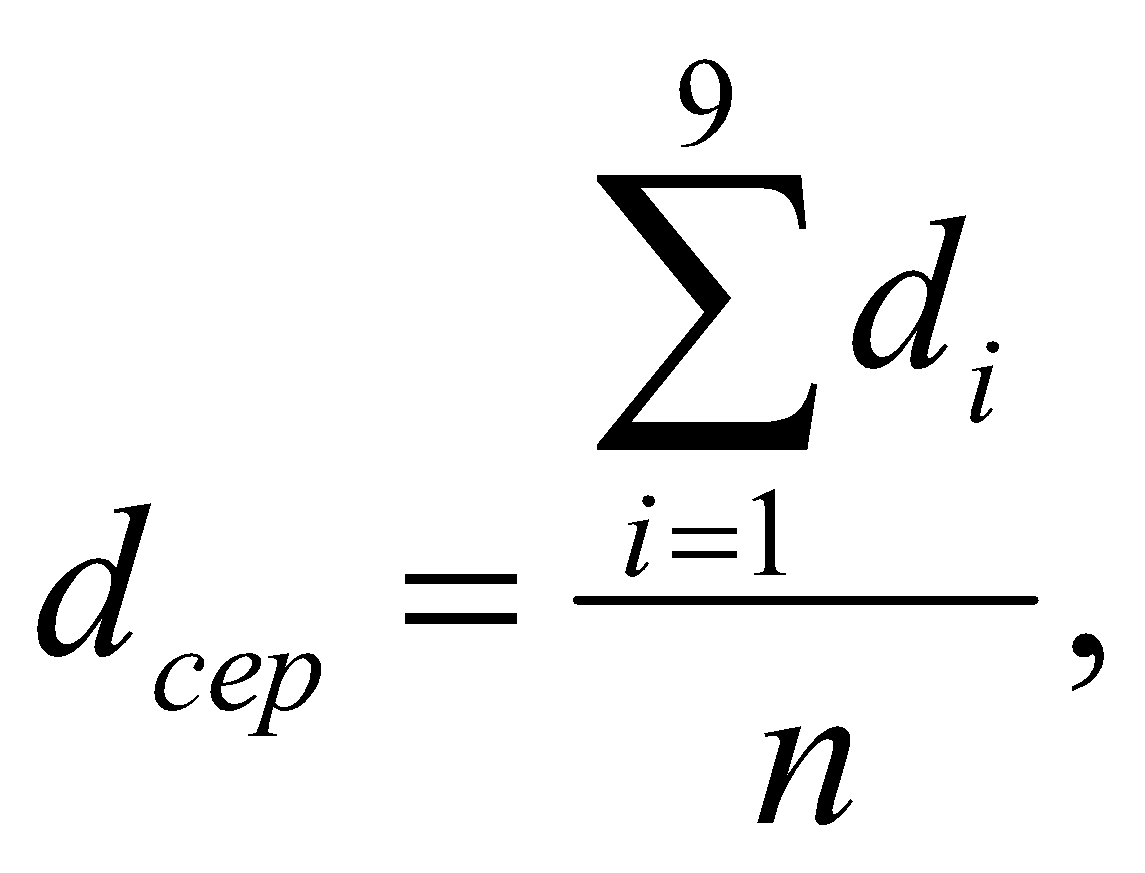

. n = 9.

Таблиця 1

Номер досліду	Відстань до екрана l, м	Порядок максимуму k	Лівий відлік, мм	Правий відлік, мм	Відстань між максимумами Xk,мм	Стала дифракційної ґратки, м
						di, м		dсер, м	Δd	ε, %
1	0,15	1	19	19	38	0,000005035	-0,000000002	0,000005037	0.0000002306	4,57
		2	39	40	79	0,00000497	-0,000000067
		3	60	61	121	0,000005075	0,000000037
2	0,20	1	25	26	51	0,000005003	-0,000000034
		2	52	53	105	0,00000498	-0,000000057
		3	80	81	161	0,000005084	0,000000047
3	0,25	1	31	32	63	0,000005061	0,000000025
		2	65	66	131	0,000004994	-0,000000043
		3	99	100	199	0,000005134	0,000000097

— Обчислити відхилення кожного значення від середнього:



— Обчислити середнє квадратичне відхилення для середнього значення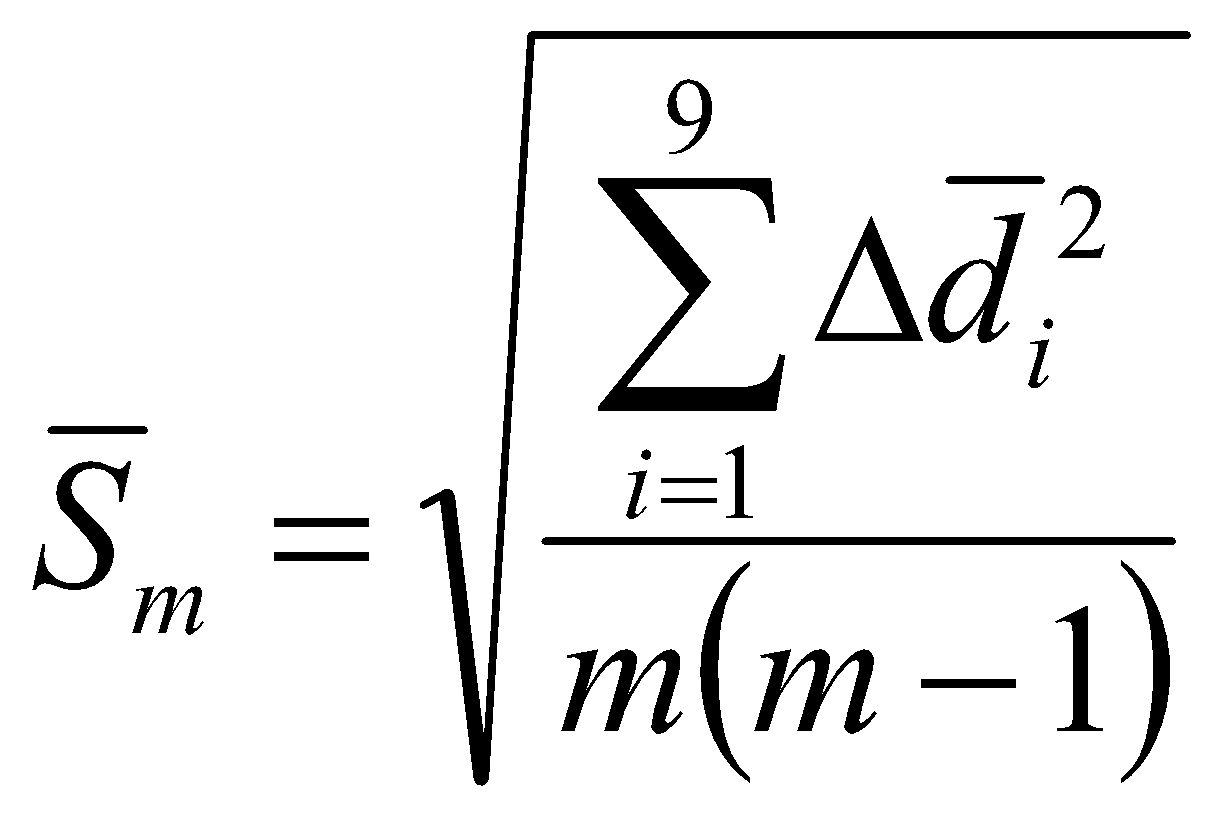

=0.0000001,

де m = 9.

— Помноживши значення на коефіцієнт Стьюдента t_Ст = 2.306 для надійної ймовірності знайти абсолютну похибку вимірювання сталої дифракційної ґратки:

.

0.0000001*2,306 = 0.0000002306

— Відносну похибку вимірювання середнього значення сталої дифракційної ґратки визначити за формулою

.
0.0000002306/0,000005037*100%=4,57%

Завдання 2. Визначити роздільну здатність дифракційної ґратки.

Обчислити кількість штрихів N та роздільну здатність R дифракційної ґратки за формулами:

,

N₁ = 0,002/0,000005037=397,06;

N₂ = 0,05/0,000005037=9 926,54.

R_1.1=1*397,06=397,06;

R_1.2=3*397,06=794,12;

R_1.3=3*397,06=1 191,18;

R_2.1=1*9 926,54=9 926,54;

R_2.2=2*9 926,54=19 853,087;

R_2.3=3*9 926,54=29 779,62;

При обчисленні ширини дифракційної ґратки l потрібно врахувати, що у формуванні дифракційної картини беруть участь лише ті штрихи, через які проходило світло, тобто лазерний промінь. Тому спершу потрібно оцінити діаметр лазерного променя (l = 2 мм) і взяти його за ширину освітленої частини ґратки. Вся ширина ґратки l = 50 мм.
Результати занести до табл. 2.

Таблиця 2

Порядок спектра k	Ширина дифрак-ційної ґратки l, м	Стала дифракційної ґратки dсер, м	Кількість штрихів ґратки N	Роздільна здатність дифракційної ґратки R
1	0,002 0,050	0,000005037	397,06 9 926,54	397,06	9 926,54
2				794,12	19 853,087
3				1 191,18	29 779,62

В исновки

У результаті виконання роботи було визначено сталу дифракційної ґратки та її роздільну здатність. Також було вивчено та опрацьовано теорії інтерференції Френеля і Фраунгофера, дифракційної ґратки, лазерів і характеристики лазерного випромінювання і методику проведення експерименту.

Дата виконання лабораторної роботи ____________________________________________

Оцінка за допуск до лабораторної роботи ________________ Підпис _________________

Оцінка за захист лабораторної роботи ___________________ Підпис _________________

ПИТАННЯ ДЛЯ ДОПУСКУ Й ЗАХИСТУ ЛАБОРАТОРНОЇ РОБОТИ
ТА ДЛЯ ПОТОЧНОГО МІКРОМОДУЛЬНОГО КОНТРОЛЮ

1. 
   Що називається дифракцією світла? Яка умова спостереження дифракції світла?
   

Дифракція світла - це поширення світлових хвиль через вузькі відкладення або перешкоди, що призводить до поширення світла в напрямках, які б не очікувалися за прямою лінією поширення світла.
Умова спостереження дифракції світла - це коли довжина хвилі світла порівнянна з розміром перешкоди, через яку воно проходить. Коли світлова хвиля зіткнулася з перешкодою, її поширення починає розходитися в усіх напрямках, створюючи інтерференційні максимуми і мінімуми на екрані або на поверхні, на якій проектується тінь. Це можна спостерігати наприклад, коли світло проходить через вузьку щілину, гострі краї перешкоди або коли світло відбивається від кристалічних решіток.

2. 
   Чим відрізняються умови спостереження дифракції Френеля і дифракції Фраунгофера?
   

Дифракція Френеля та дифракція Фраунгофера - це два типи дифракції світла на перешкоді. Основна відмінність між ними полягає у тому, яким чином світло падає на перешкоду і як спостерігається дифракційна картина.
Умови спостереження дифракції Френеля:

1. 
   Джерело світла та перешкода знаходяться на близькій відстані одна від одної.
   
2. 
   Світло падає на перешкоду під малим кутом.
   
3. 
   Дифракційні картина формується на відносно близькій відстані від перешкоди.
   
4. 
   Дифракційна картина має яскраві плями, які поступово перетворюються в темні плями при збільшенні відстані від перешкоди.
   

Умови спостереження дифракції Фраунгофера:

1. 
   Джерело світла та перешкода знаходяться на відстані один від одного.
   
2. 
   Світло падає на перешкоду під широким кутом.
   
3. 
   Дифракційна картина формується на відносно великій відстані від перешкоди.
   
4. 
   Дифракційна картина має рівномірні смуги світла та темряви, які залежать від розміру перешкоди.
   

Отже, дифракція Френеля та Фраунгофера відрізняються характером спостережень, джерелом світла та відстанню між ним та перешкодою, а також розміром дифракційних плям і полос.

3. 
   У чому полягає принцип Гюйгенса—Френеля?
   

Принцип Гюйгенса-Френеля - це один з фундаментальних принципів фізики, що описує поширення хвиль, таких як світло, звук, радіохвилі тощо.
Згідно з цим принципом, кожен елемент хвилі може бути розглянутий як джерело нових хвиль. Коли хвиля розповсюджується через середовище, кожна точка хвилі може бути розглянута як центр сферичної хвилі, яка випромінює нову хвилю в усі напрямки. Ці сферичні хвилі називаються хвильовими фронтами.
Застосування принципу полягає у тому, що для обчислення характеристик хвилі (наприклад, її амплітуди та фази) в будь-якій точці простору можна скласти суму вкладів усіх джерел хвилі в цій точці. Цей принцип є основою багатьох методів розрахунку поширення світла, зокрема дифракції та розсіювання.
Принцип Гюйгенса-Френеля знайшов своє застосування в таких галузях, як оптика, електродинаміка, акустика та радіотехніка.

4. 
   У чому полягає метод зон Френеля?
   

Метод зон Френеля - це апроксимаційний метод, що використовується в оптиці для аналізу дифракції світла на круглих або діафрагмових отворах та інших геометричних об'єктах.
Метод полягає в розбитті початкового діафрагмового відкриття на безліч зон Френеля, кожна з яких представляє ділянку діафрагми, з якої світло поширюється з фазовим зсувом, що дорівнює половині довжини хвилі.
Для кожної зони Френеля, дифракційний інтеграл обчислюється як сума вкладів точок на зоні, де фазовий зсув відносно точки в центрі діафрагми є однаковим. Оскільки фазовий зсув може бути лише кратним півхвилі, зони Френеля складаються з концентричних кіл з різним радіусом, що відповідає цілим числам півхвиль.
Після обчислення внеску кожної зони Френеля, можна знайти кінцеве розподілення світла в дифракційній площині. Цей метод дозволяє описати дифракцію світла на круглих або діафрагмових отворах з високою точністю, зокрема, визначити розміри дифракційних плям та інші параметри.
Метод зон Френеля знайшов своє застосування в багатьох галузях оптики, включаючи мікроскопію, спектроскопію та лазерну технологію.

5. 
   Застосуйте метод зон Френеля для поширення світла в однорідному ізотропному середовищі.
   

Метод зон Френеля застосовується для дифракції світла на об'єктах, що мають обмежену форму, таких як діафрагми та круглі отвори. Однак для поширення світла в однорідному ізотропному середовищі, дифракційні ефекти зазвичай знехтувані, оскільки світло не відбивається та не згинається на межі різних середовищ.
Застосування методу зон Френеля для поширення світла в однорідному ізотропному середовищі може бути здійснене тільки в тому випадку, якщо в середовищі знаходяться перешкоди, наприклад, з круглим або іншим обмеженим відкриттям.
Розглянемо приклад поширення світла через круглий отвір у плоскій перегородці, що розділяє два однорідні ізотропні середовища. Розташуємо дифракційну площину в площині перегородки, паралельної круговому отвору.
Дифракційна площина поділяється на безліч зон Френеля, кожна з яких представляє ділянку площини, з якої світло поширюється з фазовим зсувом, що дорівнює половині довжини хвилі. Радіус кожної зони Френеля може бути знайдений з формули:
r(n) =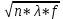
де r(n) - радіус n-ої зони Френеля, 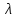- довжина хвилі світла, f - фокусна відстань кругового отвору, а n - ціле число.
Потім можна обчислити фазовий зсув світла на кожній зоні Френеля. Якщо фазовий зсув на зоні дорівнює цілому числу півхвиль, то відповідна зона внесе додаткову конструктивну інтерференцію до кінцевого результату.

6. 
   Застосуйте метод зон Френеля для дифракції на круглому отворі і непрозорому диску.
   

Розглянемо дифракцію світла на круглому отворі діаметром D та непрозорому диску з таким же діаметром, розташованих в однорідному ізотропному середовищі. Для застосування методу зон Френеля, необхідно визначити радіус першої зони Френеля:
r(1) =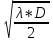
де 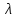- довжина хвилі світла.
Для кругового отвору діаметром D, це означає, що центральна зона Френеля буде мати радіус r(1) = D/2.
Після визначення радіуса першої зони Френеля, можна визначити радіуси наступних зон Френеля:
r(n) =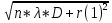
де n - ціле число, що представляє порядковий номер зони Френеля.
Після визначення радіусів зон Френеля можна обчислити фазовий зсув світла на кожній зоні Френеля, використовуючи формулу:
phi(n) = 2 * pi * r(n) /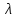
де phi(n) - фазовий зсув на n-ій зоні Френеля.
За допомогою цих фазових зсувів можна визначити інтерференційні ефекти на кінцевому зображенні. Для круглого отвору, це приведе до появи світлого диска в центрі зображення з темним кільцем навколо нього. Для непрозорого диску, це приведе до появи темного диска в центрі зображення з світлим кільцем навколо нього.
Цей ефект може бути використаний для аналізу та вимірювання діаметру круглих об'єктів, таких як бактерії, клітини та інші мікроскопічні структури.

7. 
   Виведіть формулу умови максимуму і мінімуму для дифракції на щілині.
   

Умова максимуму та мінімуму для дифракції на щілині може бути виведена з допомогою принципу Гюйгенса-Френеля та розглядуваних точок на щілині.
Розглянемо площинну хвилю, що поширюється з напрямком k на щілину ширини b. На поверхні щілини можна визначити дифракційну хвилю, що розповсюджується у всі напрямки. Ця хвиля буде мати амплітуду, яка пропорційна амплітуді падаючої хвилі та відстані між розглядуваною точкою на щілині та точкою спостереження на екрані. При цьому, фазовий зсув між різними точками на щілині та точкою спостереження може бути обчислений з принципу Гюйгенса-Френеля.
З розглядуваної точки спостереження на екрані, можна визначити геометричні параметри щілини та зв'язати їх з фазовим зсувом між різними точками на щілині та точкою спостереження. У результаті, можна отримати формулу для умови максимуму та мінімуму дифракційної хвилі на екрані:
Умова максимуму:
b sin(theta) = m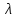
де b - ширина щілини, theta - кут нахилу до прямої, що проходить через середину щілини та точку спостереження на екрані, m - ціле число (називається порядком максимуму), та lambda - довжина хвилі світла.
Умова мінімуму:
b sin(theta) = (m + 1/2)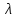
де m - ціле число (називається порядком мінімуму).
Ці умови можуть бути використані для розрахунку параметрів дифракційної картини на екрані, таких як положення максимумів та мінімумі

8. 
   Як виготовляються дифракційні ґратки? Доведіть формулу дифракційної ґратки.
   

Дисперсією дифракційної ґратки називають розбіжність у кутах, під якими спостерігається дифракційне спектральне розщеплення світла на різні спектральні складові. Ця розбіжність виникає через різний ступінь відхилення світла різних довжин хвиль від прямого напрямку при проходженні крізь ґратку.

Дисперсія дифракційної ґратки залежить від кута нахилу гратки, числа штрихів на одиницю довжини і довжини хвилі світла. Формула для розрахунку дисперсії дифракційної ґратки має наступний вигляд:



де D - дисперсія, d - відстань між сусідніми штрихами на ґратці, cos - кут дифракції і m - порядок дифракційної максимуму.

Ця формула показує, що дисперсія збільшується зі збільшенням кута дифракції та числа штрихів на одиницю довжини ґратки, але зменшується зі збільшенням порядку дифракційного максимуму.

9. 
   Що називається дисперсією дифракційної ґратки і від чого вона залежить? Виведіть формулу.
   

Дифракційні ґратки виготовляються шляхом формування періодичної структури на поверхні матеріалу, що має високу оптичну якість. Цю структуру можна отримати за допомогою фотолітографії або гравіювання на склі або металевій поверхні.
У дифракційній ґратці періодична структура складається з послідовності однакових штрихів та проміжків між ними. Штрихи мають фіксовану ширину та висоту, а проміжки між ними є також однаковими за шириною. Періодичність ґратки описується параметром d, який відповідає відстані між центрами сусідніх штрихів або проміжків.
Формула дифракційної ґратки описує залежність кута відхилення дифрактованого променя світла від початкового напрямку падіння. За умови, що промінь падає перпендикулярно до поверхні ґратки, формула може бути записана наступним чином:
d (sin(y)) = m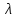
де d - період ґратки, y - кут відхилення дифрактованого променя від початкового напрямку падіння, m - ціле число, яке відповідає порядку дифракційного максимуму, та 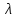- довжина хвилі світла.

10. 
    Що називається роздільною здатністю дифракційної ґратки і від чого вона залежить? Виведіть формулу.
    

Роздільна здатність дифракційної ґратки - це мінімальний кутовий розмір двох точкових джерел світла на вхідній площині, за якими можна розділити їхні дифракційні зображення на вихідній площині.
Роздільна здатність залежить від довжини хвилі світла 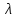та від параметрів ґратки, таких як крок d між ближніми щілинами та кількість $N$ щілин:
Роздільна здатність R дифракційної ґратки може бути визначена за допомогою формули:
R = 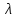Nd \cos(y)
де y - кут дифракції, який визначається як кут між прямою, що проходить через центр ґратки та точку на вихідній площині, де спостерігається дифракційне зображення, та нормаллю до ґратки.
11. Визначте максимальний порядок головного максимуму (теоретично), якщо d = 0,01 мм, λ= 5000 Å.

Для того, щоб визначити максимальний порядок головного максимуму при заданих параметрах d та L, ми можемо скористатися формулою Брэгга-Вульфа для розсіювання рентгенівських променів на кристалах:
nλ = 2d sin(θ)
де n - ціле число, λ - довжина хвилі рентгенівських променів, d - міжплощина в кристалі, а θ - кут падіння променів на кристал.
Максимальний порядок головного максимуму буде відповідати максимальному цілому числу n, яке може бути задоволене при даних значеннях d та L.
Перетворимо формулу Брэгга-Вульфа, щоб виділити n:
n = 2d sin(θ) / λ
Максимальне значення n відповідатиме куту падіння θ, при якому sin(θ) має максимальне можливе значення 1. Тоді:
n_max = 2d / λ
Підставляючи дані з завдання, отримуємо:
n_max = 2(0.01 мкм) / (5000 Å) = 0.004
Оскільки n повинне бути цілим числом, то максимальний порядок головного максимуму для даних параметрів буде n_max = 0.
12. Яке застосування дифракційної ґратки?

Дифракційні ґратки - це оптичні прилади, які використовуються для розкладання світла на його складові колірні складові (спектр). Дифракційні ґратки складаються з ряду паралельних штрихів або щілин, які сприяють дифракції світла і створенню інтерференційної картини на екрані.
Основне застосування дифракційних ґраток полягає в їх використанні для спектрального аналізу світла. Коли світло проходить через дифракційну ґратку, воно розкладається на спектральні складові з різними довжинами хвиль. Це дає можливість вивчення складу світла і визначення характеристик джерела світла.
Дифракційні ґратки також використовуються в науці і техніці для створення інтерференційної картини, яка може бути використана для вимірювання довжин хвиль світла, вимірювання кутів нахилу поверхні і дослідження структури матеріалів. В оптиці дифракційні ґратки також використовуються для створення оптичних фільтрів з певною характеристикою пропускання світла.
Дифракційні ґратки також використовуються в спектроскопії, фотометрії, лазерній техніці, оптичній телекомунікації, науці про матеріали та багатьох інших галузях науки і техніки.
13. Як за допомогою дифракції вивчається структура кристалічних тіл?

Дифракція рентгенівських променів (або дифракція електронів) використовується для вивчення кристалічної структури твердих тіл. Принцип дифракції полягає в тому, що коли рентгенівські промені або електрони проходять через кристал, вони взаємодіють з його атомами і розсіюються. Якщо кристал є досить регулярним у своїй структурі, то розсіяні промені взаємодіють між собою і інтерферують, утворюючи характерні максимуми та мінімуми на екрані.
За допомогою дифракції можна отримати інформацію про геометричну структуру кристалу, таку як відстані між атомами в кристалі, форму його елементарної клітини та орієнтацію кристалу в просторі. Ця інформація може бути використана для побудови моделі кристалічної структури твердих тіл.
Для проведення дифракційного аналізу зазвичай використовують рентгенівські промені або електрони з високою енергією, які мають коротку довжину хвилі і можуть проникати в кристал. Розсіяні промені збираються на детекторі та аналізуються для отримання інформації про кристалічну структуру.
Дифракційний аналіз є важливим інструментом для вивчення кристалічних матеріалів і знаходить застосування в багатьох галузях науки і техніки, включаючи кристалографію, матеріалознавство.
14. Як зміняться кутова дисперсія та роздільна здатність, якщо ґратку з d = 0,01 мм замінити ґраткою з d = 0,001 мм?

Роздільна здатність дифракційної ґратки залежить від довжини хвилі світла, кількості щілин та розміру кроку між ними. За умови, що довжина хвилі світла та кількість щілин залишаються незмінними, заміна ґратки з $d=0.01$ мм на ґратку з $d=0.001$ мм призведе до зменшення роздільної здатності і збільшення кутової дисперсії.
Роздільна здатність зменшиться в 10 разів, оскільки роздільна здатність зворотнопропорційна розміру кроку між щілинами d. Таким чином, заміна ґратки з d=0.01 мм на ґратку з d=0.001 мм призведе до зменшення роздільної здатності в 10 разів.
Кутова дисперсія збільшиться, оскільки кутова дисперсія дифракційної ґратки залежить від розміру кроку між щілинами/ Отже, заміна ґратки з d=0.01 мм на ґратку з d=0.001 мм призведе до збільшення кутової дисперсії в 10 разів.
15. Дайте характеристику лазерного випромінювання.

Лазерне випромінювання - це електромагнітне випромінювання, яке виробляється в лазері. Воно має декілька характеристик:

• 
  Монохроматичність: лазерне випромінювання має дуже вузький спектральний діапазон і випромінюється на одній довжині хвилі. Це дозволяє використовувати лазери для багатьох додатків, де потрібна точність і стабільність довжини хвилі, таких як медицинська діагностика, наука та технології.
  

• 
  Когерентність: лазерне випромінювання є когерентним, що означає, що всі світлові хвилі, які випромінюються, знаходяться у фазі і є узгодженими. Це дозволяє використовувати лазери для додатків, таких як інтерференційна мікроскопія, голографія та оптичні засоби з високою роздільною здатністю.
  

• 
  Напрямленість: лазерне випромінювання має високу напрямленість, що означає, що воно випромінюється в зустрічному напрямку з високою інтенсивністю. Це дозволяє використовувати лазери для різних додатків, таких як лазерна різка, лазерна зварювання та лазерна обробка матеріалів.
  

• 
  Висока інтенсивність: лазерне випромінювання може мати високу інтенсивність, що дозволяє використовувати лазери для додатків, таких як лазерна терапія, наука та дослідження фізики високих енергій.
  

• 
  Монодисперсність: лазерне випромінювання має вузький діапазон досмірної ширини, що відноситься до ширини функції пучка. Це дозволяє використовувати лазери для додатків, де необхідна висока просторова роздільна здатність, таких як мікроскопія, оптичні датчики та дистанційне зондування.
  

Узагальнюючи, лазерне випромінювання має унікальні властивості, які роблять його корисним для багатьох різних додатків. Лазерна технологія широко використовується у науці, медицині, інженерії та технологіях і знаходить все більше застосування у сучасному світі.
16. Фізичні основи випромінювання гелій-неонового лазера.

Гелій-неоновий (He-Ne) лазер - це газовий лазер, що випромінює в інфрачервоній, видимій і ультрафіолетовій областях спектру. Фізичні основи випромінювання He-Ne лазера полягають у розподілі енергії атомів газу в різних енергетичних станах, залежно від температури та струму, що протікає через газову розрядну трубку.
He-Ne лазер має трубку з газом, який складається з суміші гелію та неону під високим тиском. Гелій заповнює трубку на висоті 85%, а неон - на висоті 15%. Крім того, трубка містить дві зеркальні поверхні на кінцях, що утворюють резонатор. Одна з цих поверхонь - повністю відбиваюча, а інша - частково пропускаюча.
При подачі струму в газову розрядну трубку відбувається іонізація газу, тобто відбувається збудження електронів в атомах газу до вищих енергетичних станів. Коли електрони повертаються на більш низькі енергетичні рівні, вони випромінюють енергію у вигляді світла.
У He-Ne лазері газ випромінює світло з довжиною хвилі 632,8 нм, що відповідає червоному кольору. Це світло є монохроматичним та когерентним, оскільки всі фотони мають однакову фазу та напрямок. Це досягається завдяки тому, що внутрішня форма трубки забезпечує лазерну дію, тобто збудження атомів газу залишається у резонаторі, збільшуючи кількість випромінюваних фотонів та підсилюючи їх фазу.
Оскільки світло в He-Ne лазері є когерентним, воно може бути застосовано для різних цілей. Наприклад, він використовується для вирівнювання, для зчитування баркодів, в технології лазерного сканування та інших застосуваннях, які потребують монохроматичного та когерентного світла.
У He-Ne лазері використовуються високовольтні випромінювачі для забезпечення струму, необхідного для збудження газу, а також зеркала для створення резонатора. Для підсилення світла використовуються оптичні підсилювачі, які змінюють форму світла, що виходить з лазера, для його більш ефективної передачі на далекі відстані.
У загальному, He-Ne лазер - це досить простий та дешевий лазер, який може забезпечити монохроматичне та когерентне світло в зручному форматі. Це забезпечує його популярність в багатьох різних дисциплінах, від науки до технологій та медицини.
17. Чому в даній роботі після ґратки не ставиться лінза для формування дифракційної картини?

Після ґратки не ставиться лінза для формування дифракційної картини, оскільки дифракційна ґратка сама за собою вже є об'єктивом, який формує дифракційну картину.

Дифракційна ґратка пропускає світло через свої вузькі відкриття, які вчиняють як інтерференційні елементи, формуючи інтерференційну картину на екрані або детекторі. Ця дифракційна картинка може бути знята та досліджена, не використовуючи лінзу, оскільки формування картини вже здійснюється за допомогою ґратки.
18. Як необхідно змінити лабораторну роботу, щоб збільшити роздільну здатність ґратки?

Щоб збільшити роздільну здатність ґратки, необхідно зробити наступні кроки:
Збільшити кількість штрихів на ґратці. Роздільна здатність ґратки пропорційна кількості штрихів на ній. Таким чином, збільшення кількості штрихів може покращити роздільну здатність.
Зменшити розмір штрихів на ґратці. Роздільна здатність ґратки пропорційна розміру штрихів на ній. Таким чином, зменшення розміру штрихів може покращити роздільну здатність.
Використовувати більш вузькосмугове джерело світла. Роздільна здатність ґратки пропорційна довжині хвилі світла, яке проходить через неї. Таким чином, використання більш вузькосмугового джерела світла може покращити роздільну здатність.
Зменшити довжину хвилі світла. Роздільна здатність ґратки пропорційна довжині хвилі світла, яке проходить через неї. Таким чином, використання світла з меншою довжиною хвилі може покращити роздільну здатність.