Главная страница
Навигация по странице:

  • Измерить физическую величину

  • Выделяют следующие виды погрешностей

  • Абсолютная погрешность

  • Относительная погрешность

  • Приведенная погрешность

    		•

    Лабораторная работа1. Лабораторная работа Определение ускорения свободного падения с помощью математического маятника


    Скачать 28.66 Kb.
    НазваниеЛабораторная работа Определение ускорения свободного падения с помощью математического маятника
    Дата02.06.2022
    Размер28.66 Kb.
    Формат файлаdocx
    Имя файлаЛабораторная работа1.docx
    ТипЛабораторная работа
    #566470

    Лабораторная работа № 1.

    Определение ускорения свободного падения с помощью математического маятника.

    Цель работы: научиться рассчитывать погрешности прямых и косвенных измерений.

    Приборы и материалы: 1) секундомер; 2) линейка; 3) математический маятник.

    Порядок выполнения работы0

    Упражнение 1. Измерение длины математического маятника.

    1) С помощью линейки измерим длину математического маятника l. Измерения проводим 5 раз.

    2) Результаты измерений занесем в таблицу:

    № п/п
    li, мм
    (- li), мм
    (- li)2, мм2

    1
    112
    8
    64

    2
    105
    1
    1

    3
    100
    4
    16

    4
    110
    6
    36

    5
    97
    7
    49


    3) Определим среднее значение длины маятника: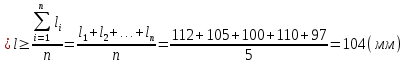



    (где n – число измерений) и продолжим заполнять таблицу.

    Вычислим абсолютную систематическую погрешность измерения длины математического маятника по формуле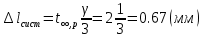



    Здесь t,p=2 – коэффициент Стьюдента определяется по таблице, =1 мм - цена деления линейки.

    4) Вычислим абсолютную случайную погрешность измерения длины математического маятника по формуле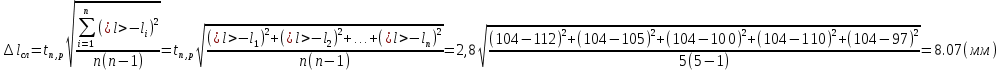



    Здесь tn,p =2.8– коэффициент Стьюдента определяется по таблице (n=5 - число измерений, p=0,95 - надежность или вероятность).

    5) Вычислим общую абсолютную погрешность измерения длины математического маятника по формуле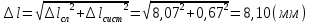



    6) Запишем результат измерения длины математического маятника в виде l=±Δl= 104.00±8.10 мм с надежностью p=0,95.
    Упражнение 2. Измерение времени двадцати колебаний математического маятника.

    1. С помощью секундомера измерили время  двадцати колебаний математического маятника. Измерения произвели не менее 5 раз.

    2) Результаты измерений занесли в таблицу:

    № п/п
    τi, с
    (<τ>- τi), с
    (<τ>- τi)2, с2

    1
    83
    0,6
    0,36

    2
    84
    0,4
    0,16

    3
    84
    0,4
    0,16

    4
    85
    1,4
    1,96

    5
    82
    1,6
    2,56


    3) Определим среднее значение времени двадцати колебаний математического маятника по формуле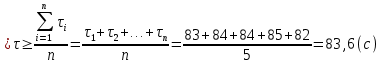



    (где n=5 – число измерений) и продолжим заполнять таблицу.

    4) Вычислим абсолютную систематическую погрешность измерения времени двадцати колебаний математического маятника по формуле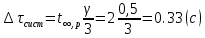



    Здесь t,p =2– коэффициент Стьюдента определяется по таблице, =0,5 с - цена деления секундомера.

    5) Вычислим абсолютную случайную погрешность измерения времени двадцати колебаний математического маятника по формуле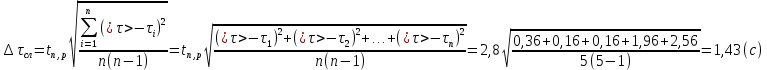



    Здесь tn,p =2,8– коэффициент Стьюдента определяется по таблице.

    6) Вычислим общую абсолютную погрешность измерения времени двадцати колебаний математического маятника по формуле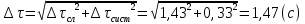


    7) Запишем результат измерения времени двадцати колебаний математического маятника в виде τ=<τ>±Δτ= 83,60±1,47 с с надежностью p=0,95.
    Упражнение 3. Определение периода колебаний математического маятника.

    1) Определим среднее значение периода колебаний математического маятника по формуле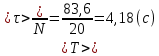

    , где N – число колебаний математического маятника (в нашем случае 20).

    2) Вычислим абсолютную погрешность измерения периода колебаний математического маятника по формуле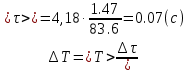



    3) Запишем результат измерения периода колебаний математического маятника в виде T   T=4,18±0.07 c
    Упражнение 4. Определение ускорения свободного падения.

    1) Определим среднее значение ускорения свободного падения по формуле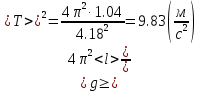



    2) Вычислим абсолютную погрешность измерения ускорения свободного падения по формуле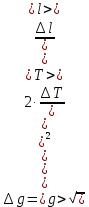


    3) Запишем результат измерения ускорения свободного падения в виде g  g  g= 9,83±0,34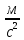

    4) Вывод: в ходе работы экспериментально определили ускорение свободного падения с помощью математического маятника, научились рассчитывать погрешности прямых (длина и время) и косвенных (ускорение свободного падения) измерений с заданной точностью. В результате получили, что ускорения свободного падения равно g  g  g= 9,83±0,34 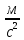. Полученные результаты несущественно отличаются от табличных g  g  g= 9,81 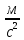. Погрешность связана с неточностью при измерениях.
    Контрольные вопросы

    1) Что называется измерением физической величины? Какие измерения бывают?

    Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.

    Измерения бывают:

    1. Прямые -если физическая величина измеряется непосредственно путем снятия данных со шкалы прибора.

    2. Косвенные - если физическая величина определяется по формуле.


    2) Назовите виды погрешностей и дайте им характеристику.

    Разница между результатом измерения и истинным значением измеряемой величины называется погрешностью измерения.

    Причем чем погрешность меньше, тем считается выше точность.

    Факторов, оказывающих влияние на точность измерения, существует огромное множество. Следовательно, любая классификация погрешностей измерения достаточно условна, поскольку нередко в зависимости от условий измерительного процесса погрешности могут проявляться в различных группах.

    Выделяют следующие виды погрешностей:

    1) абсолютная погрешность;

    2) относительна погрешность;

    3) приведенная погрешность;

    4) основная погрешность;

    5) дополнительная погрешность;

    6) систематическая погрешность;

    7) случайная погрешность;

    8) инструментальная погрешность;

    9) методическая погрешность;

    10) личная погрешность;

    11) статическая погрешность;

    12) динамическая погрешность.

    Абсолютная погрешность – это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.

    Абсолютная погрешность вычисляется по следующей формуле:

    Δхn = хn − х0,

    где хn – значение некой величины, полученное в процессе измерения;

    х0 – значение той же самой величины, принятое за базу сравнения (настоящее значение).

    Относительная погрешность – это число, отражающее степень точности измерения.

    Относительная погрешность вычисляется по следующей формуле: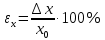



    где Δх – абсолютная погрешность; х0 – настоящее (действительное) значение измеряемой величины.

    Относительная погрешность выражается в процентах.

    Приведенная погрешность – это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению.

    Инструментальная погрешность – это погрешность, возникающая из-за допущенных в процессе изготовления функциональных частей средств измерения ошибок.
    3) Что такое доверительный интервал? Как определяются его границы?

    Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью a (0 < a < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина a – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение. Половина ширины доверительного интервала представляет собой случайную погрешность.
    4) Объясните, как рассчитываются погрешности прямых и косвенных измерений.

    При прямых измерениях за абсолютную погрешность прирнимают инструментальную погрешность, которую определяют по классу тоности или цене деления.

    Обработку результатов косвенных измерений следует выполнять в следующей последовательности: 1. Найти значения входящих в расчетную формулу величин, а также их абсолютную и относительную погрешности

    2. По уравнению вычислить значение z измеряемой величины при измеренных значениях аргументов.

    3. Вывести формулу для расчета погрешности искомой величины z как функции погрешностей прямо измеренных величин.
    Список литературы

    1. Руководство к лабораторным занятиям по физике. Под ред. Л.Л. Гольдина. – М.: Наука, 1973.- с. 11-26. 2. Кибец И.Н., Кибец В.И. Физика: Справочник. – Харьков: Фолио; Ростов н/Д: Феникс, 1997. – с. 14-20

    написать администратору сайта