Лабораторная работа 02

• Название: Лабораторная работа 02
• Дата: 23.03.2022
• Размер: 89.56 Kb.
• Имя файла: Lab_1_02.docx
• Тип: Документы; #411945
• страница: 1 из 5

ЦентрФизикиФТФИТМО

Лабораторная работа № 1.02

Изучение скольжения тележки по наклонной плоскости

Цель работы

1. 
   Экспериментальная проверка равноускоренности движения те- лежки по наклонной плоскости.
   
2. 
   Определение величины ускорения свободного падения 𝑔.
   

Введение

Как известно, при поступательном равноускоренном движе- нии тела вдоль оси 0 зависимость проекции его скорости от времени определяется выражением:
() = ₀ + 𝑎 (1)

где ₀ - проекция скорости на ось 0 в момент времени = 0,

𝑎 - ускорение тела. Зависимость координаты тела от времени

имеет вид:

() = ₀ + ₀ +

𝑎²


2

. (2)

Здесь ₀ - начальная координата. Если начальная скорость тела равна нулю, то из (2) следует:
𝑎 2 2


(︀ )︀
₂ − ₁ = _{2 2} − ₁ . (3)

Таким образом, существует линейная зависимость между пе- ремещением = ₂ − ₁ и полуразностью квадратов значений

времени 2 −2 . Коэффициент пропорциональности этой зависимо-

2 1

2

сти равен ускорению тела. Если экспериментальный график этой

зависимости будет представлять собой прямую линию, то это бу- дет доказательством движения с постоянным ускорением.

В качестве объекта совершающего равнопеременное поступа- тельное движение рассмотрим тележку, скользящую по наклонной плоскости (см. рис.1). Второй закон Ньютона, описывающий ее движение, имеет вид:
⃗𝑎 = ⃗𝑔 + 𝑁^⃗ + 𝐹^⃗_тр (4)

где ⃗𝑎 – ускорение тележки,

_𝑁⃗

- сила реакции опоры, а сила

трения, возникающая при скольжения, по модулю равна про- изведению коэффициента трения на силу нормальной реакции:

𝐹_тр = 𝜇𝑁 . Проекции уравнения (4) на координатные оси:

{︃
0 : 0 = 𝑁 − 𝑔 cos 𝛼

0 : 𝑎 = 𝑔 sin 𝛼 − 𝜇𝑔 cos 𝛼

(5)

где 𝛼 - угол между наклонной плоскостью и горизонталью. Из

(5) следует выражение для модуля ускорения:
𝑎 = 𝑔 sin 𝛼 − 𝜇𝑔 cos 𝛼 (6)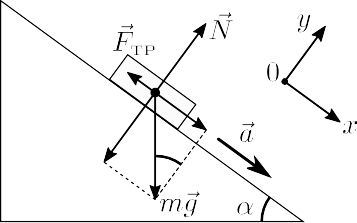



РИС. 1. Векторная диаграмма сил, действующих на тело, расположенное на наклонной плоскости
Поскольку в лабораторной установке коэффициент трения 𝜇 и угол 𝛼 достаточно малы, то cos 𝛼 в формуле (6) можно заменить единицей. С учетом этого выражение для ускорения будет иметь вид:

𝑎 = 𝑔 (sin 𝛼 − 𝜇) . (7)

Таким образом, теоретическая зависимость ускорения 𝑎 от sin 𝛼 является линейной и угловой коэффициент этой зависимо- сти равен ускорению свободного падения 𝑔.