Главная страница
Навигация по странице:

  • Изучение равноускоренного движения.

  • Приборы и принадлежности

  • Методика определения ускорения движения грузов.

  • Рис.1 Зависимость времени падения груза от высоты

  • Рис.2 Зависимость времени падения от массы перегрузка

    		•

    Лабораторная работа 103. Изучение законов равноускоренного движения. Исполнитель Студент, группы 13а72( ) Бабаев П. А. подпись


    Скачать 173.5 Kb.
    НазваниеЛабораторная работа 103. Изучение законов равноускоренного движения. Исполнитель Студент, группы 13а72( ) Бабаев П. А. подпись
    Дата20.03.2018
    Размер173.5 Kb.
    Формат файлаdoc
    Имя файла1_03.doc
    ТипЛабораторная работа
    #38995

    Министерство образования Российской Федерации
    ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

    Наименование факультета – ЕНМФ

    Наименование выпускающей кафедры – Общая физика
    Наименование учебной дисциплины - Физика

    Лабораторная работа № 1-03.
    «Изучение законов равноускоренного движения».

    Исполнитель:

    Студент, группы 13а72(_______) Бабаев П.А.

    подпись

    (_______)

    дата

    Руководитель, профессор (_______)

    Должность, ученая степень, звание подпись

    (_______)

    дата

    Томск –2007

    Изучение равноускоренного движения.
    Цель работы: изучение динамики поступательного движения связанной системы тел с учетом силы трения; оценка силы трения как источника систематической погрешности при определении ускорения свободного падения на лабораторной установке.

    Приборы и принадлежности: установка «Машина Атвуда», набор грузов, электронный секундомер.

    Теоретическое введение.

    Ускорение свободного падения g можно найти с помощью простого опыта: бросить тело с известной высоты h и измерить время падения t, я затем из формулы h=gt2/2 вычислить g.

    Основная задача, которая стоит перед экспериментатором при определении ускорения свободного падения g описываемым методом, состоит в выборе оптимального соотношения между высотой падения и временем падения. Существует способ, который позволяет при небольшой высоте падения, чтобы можно было пренебречь сопротивлением воздуха, сделать время падения большим по сравнению с тем, которое при непосредственном падении тела с этой высоты получилось бы.

    Такой способ реализован в приборе, который называется «Машина Атвуда». Суть работы состоит в следующем. Через блок перекинута нить, на которой закреплены грузы массой M каждый. На один из грузов кладется перегрузок массой m. Ускорение груза легко найти, если ввести 2 предположения:

    1.Блок и нить невесомы, т.е. их массы равны 0;

    2.Трением тела о воздух и трением между блоком и его осью можно пренебречь.

    С учетом этого уравнения движения груза имеют вид:

    Mg-T=-Ma,

    (M+m)g-T=(m+M)a, (1)

    где T – сила натяжения нитей, a – ускорение грузов.

    Из уравнений (1) получаем

    а=g (2)

    (3)

    Время, за которое груз (m+M) опускается на высоту h, равно

    . (4)

    Легко видеть, что чем меньше m и больше M, тем больше t. Если мы выполним это условие, то получим новую проблему. Тяжелые грузы приведут к увеличению силы трения в блоке, что потребует увеличение перегрузка, и т.д.

    Получим соотношение, связывающее M, m и коэффициент трения в оси блока. Для этого введем понятие перегрузка m0, который только-только приводит в движение систему грузов. В условиях равновесия момент сил натяжения нитей (T2 – T1)*R равен моменту сил трения Mтр, где T1=M*g; T2=(M+m0)*g; R – радиус блока, а Mтр=*N*r, где N – реакция блока;

    N=T1+T2=(2M+m0)g;

    r – радиус оси блока. Из этих условий находят следующее соотношение:

    . (5)

    Анализируя (5), приходим к выводу, что m не может быть сколько угодно малой, чтобы удовлетворить требованию больших значений времени. Окончательно формулу (2) можно применять, если m. Интуитивно заключают, что трение пренебрежимо мало, если m>>m0.
    Методика определения ускорения движения грузов.

    Измерения проводят с перегрузками, превышающими в 35 раз по массе m0. Необходимо убедиться, что в этом случае выполняется зависимость h=. Для этого переписывают это уравнение в виде

    t=. (6)

    Если положить y=t, x=, то получится прямая вида y=kx, где k=, которая проходит через начало координат. Прямая y=f(x) или t=f*() может быть построена по экспериментальным точкам. Для этого выбирают один перегрузок m и различные высоты h. Измерение времени для одной и той же высоты проводят несколько раз. На оси ординат откладывают значение t, на оси абсцисс - . Если полученные экспериментальные точки ложатся на прямую, то движение системы тел можно считать равноускоренным. По наклону прямой находят коэффициент k в виде соотношения k=, где - отрезок по оси y и - соответствующий ему отрезок по оси x. Получают равенство
    (7)

    Из уравнения (7) определяют a. Убеждаются, что его значение действительно меньше g.

    Экспериментальной проверки легко подвергнуть уравнение (4)

    t= (8)

    Если выбрать оси координат y=t и x=, вновь можно получить уравнение прямой у=, проходящей через начало координат и имеющей наклон ;

    g=. (9)

    Измерения и погрешности: Таблица 1

    h, м
    t1, c
    t2, c
    t3, c
    t4, c
    Ср.зн
    m, кг
    m0, кг
    Примечания

    0,38
    2,17
    2,98
    2,38
    2,32
    2.46
    0,105
    0,0027
    α=0,95

    0,36
    2,72
    2,23
    2,04
    2,31
    2.33
    0,105
    0,0027
    h=0,001

    0,34
    2,39
    2,2
    2,43
    2,02
    2.26
    0,105
    0,0027
    n=5

    0,32
    2,03
    2,27
    1,73
    1,84
    1.97
    0,105
    0,0027
    t=2,78

    0,3
    2,25
    1,9
    2,35
    1,87
    2.09
    0,105
    0,0027
     

    Приб.погр
    σ(t)
    ∆t(сл)
    ∆t'
    e(t), %
     
     
     
     

    0,00095
    0.13793
    1.05779
    1.057790427
    42.9996
     
     
     
     

     
    0.11104
    0.68555
    0.685548658
    29.4227
     
     
     
     

     
    0.07314
    0.29746
    0.297461517
    13.162
     
     
     
     

     
    0.09168
    0.46732
    0.467318966
    23.7218
     
     
     
     

     
    0.09426
    0.49401
    0.494006913
    23.6367
     
     
     
     



    Метод наименьших квадратов:


    Метод наименьших квадратов для графика (рис.1) Таблица 2



    y=∆t
    x=h^0,5
    a, м\с2
    k
    b

    2,4625
    0,6164
    0,308629
    9,752546
    -3,549

    2,325
    0,6
    0,309677
     
     

    2,26
    0,5831
    0,300885
     
     

    1,9675
    0,5657
    0,325286
     
     


    ,


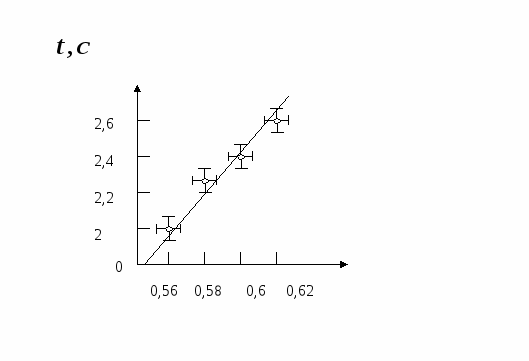    Рис.1 Зависимость времени падения груза от высоты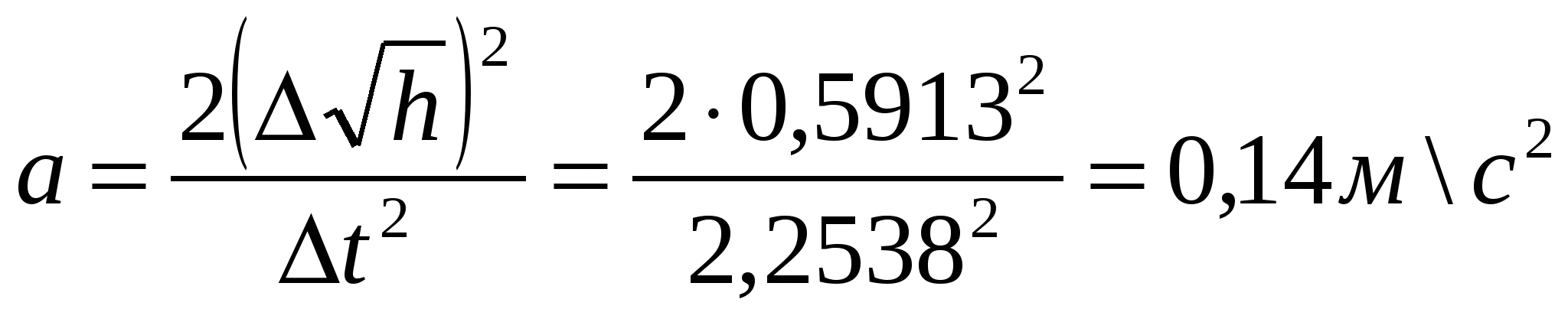


    Измерения и погрешности Таблица 3

    №изм
    m, кг
    М/m
    t1, c
    t2, c
    t3, c
    t4, c
    Ср.зн
    m, кг
    m0, кг
    Прим

    1
    0,0027
    38,9
    2,32
    2,47
    2,92
    2,2
    2.48
    0,105
    0,0027
    α=0,95

    2
    0,0054
     
    1,97
    1,8
    1,84
    1,48
    1.77
    0,105
    0,0027
    h=0,001

    3
    0,0081
    13
    1,24
    1,28
    1,33
    1,19
    1.26
    0,105
    0,0027
    n=5

    4
    0,0108
    9,7
    1,03
    1,1
    1,04
    1,14
    1.08
    0,105
    0,0027
    t=2,78

    5
    0,0135
    7,8
    1,02
    0,9
    1,07
    0,98
    0.99
    0,105
    0,0027
     

    Пр.погр
    σ(t)
    ∆t(сл)
    ∆t'
    e(t), %
     
     
     
     
     
     

    0,00095
    0.122
    0.33917
    0.33917
    13.6763
     
     
     
     
     
     

     
    0.08059
    0.22404
    0.22405
    12.658
     
     
     
     
     
     

     
    0.02302
    0.064
    0.06401
    5.07996
     
     
     
     
     
     

     
    0.02012
    0.05595
    0.05595
    5.18097
     
     
     
     
     
     

     
    0.02784
    0.07739
    0.0774
    7.81796
     
     
     
     
     
     


    Метод наименьших квадратов (рис.2) Таблица 4


    №
    x
    y
    k
    b

    1
    38,9
    1,64
    0,004041
    1,35880137

    2
    19,4
    1,516
     
     

    3
    13
    1,51
     
     

    4
    9,7
    1,398
     
     




    Рис.2 Зависимость времени падения от массы перегрузка
    g=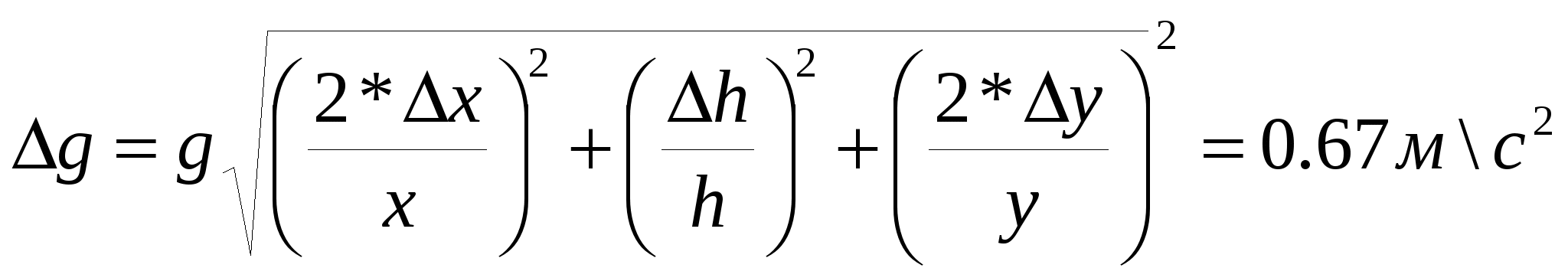=10.46 м/с2





    Вывод: в результате проведения лабораторной работы мы провели эксперимент по изучению динамики поступательного движения связанной системы тел с помощью установки «Машина Атвуда». Также мы рассчитали ошибку измерений и определили ускорение свободного падения на данной лабораторной установке. Из рисунков 1 и 2 следует, что в пределах доверительных интервалов график аппроксимируется в линию, следовательно законы равноускоренного движения выполняются. В свою очередь по наклонам прямых на графиках, были определены ускорение а и ускорение свободного падения g.

    написать администратору сайта