ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА ОСНОВЕ МАЯТНИКА ОБЕРБЕКА. Лабораторная работа 1. 1 Проверка основного закона динамики вращательного движения на основе маятника обербека
 Скачать 186.55 Kb. Скачать 186.55 Kb.
|
|
Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный университет телекоммуникаций и информатики» (СибГУТИ) Кафедра физики Лабораторная работа №1.1 ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА ОСНОВЕ МАЯТНИКА ОБЕРБЕКА Выполнил студент:  (группа) (Фамилия Имя Отчество) Проверил преподаватель:  (должность) (Фамилия Имя Отчество)  Измерения сняты: Измерения сняты: (дата) (подпись) (расшифровка подписи)  Отчет принят: Отчет принят: (дата) (подпись) (расшифровка подписи) Работа зачтена:  (оценка) (дата) (подпись) (расшифровка подписи) Новосибирск, 2021 г. Цель работы Изучить законы вращательного движения. Определить собственный момент инерции маятника Обербека (крестовины). Исследовать зависимость момента инерции грузов на крестовине от расстояния. Основные теоретические сведения Вращательным движением твердого тела называется такой вид движения, при котором каждая точка тела описывает окружности вокруг некоторой прямой, называемой осью вращения. Основным законом динамики вращательного движения является связь момента силы с моментом инерции I и угловым ускорением β: 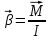 Этот закон является отображением второго закона Ньютона для вращательного движения. Направление вектора углового ускорения  совпадает с направлением момента сил совпадает с направлением момента сил 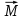 , который в свою очередь совпадает с осью вращения. , который в свою очередь совпадает с осью вращения.Момент инерции тела является мерой инертности тела во вращательном движении, аналогично тому, как масса тела является мерой его инертности при поступательном движении. Для материальнойточкимомент инерции определяется как произведение массы на квадрат расстояния от оси вращения до центра масс тела: 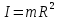 Чтобы определить момент инерции системы из N материальных точек, вращающихся относительно некоторой неподвижной оси, нужно найти сумму моментов инерции всех материальных точек относительно этой оси:  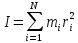 где mi— масса i-й точки, ri— расстояние от i-й точки до оси вращения. Длятвердоготеласуммирование нужно проводить для всех точек тела, следовательно, сумма заменяется интегралом: 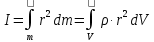 где dm = ρdV масса малого элемента объема тела dV, ρ – плотность, r – расстояние от элемента dV до оси вращения. Моментом силы относительно оси вращения называется векторное произведение величин: 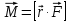 где 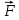 - сила, действующая на тело, - сила, действующая на тело, 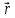 - расстояние от оси вращения до точки приложе ния силы. Направление вектора - расстояние от оси вращения до точки приложе ния силы. Направление вектора 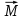 перпендикулярно плоскости, в которой лежат вектора перпендикулярно плоскости, в которой лежат вектора 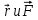 в соответствии с правилом векторного произведения и совпадает с направле нием поступательного движения правого винта при его повороте от в соответствии с правилом векторного произведения и совпадает с направле нием поступательного движения правого винта при его повороте от 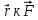 на угол, меньший π. Значение вектора на угол, меньший π. Значение вектора 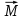 может быть определено как (рис.1.1): может быть определено как (рис.1.1):M= F*r*sinα, 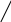 где r*sinα = lплечо приложения силы 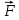 . . 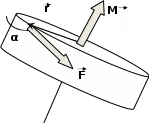 Рисунок 1.1. Иллюстрация к определению момента силы Описание лабораторной установки Законы вращательного движения проверяются на установке, называемой маятником Обербека‚ который представляет собой крестовину, вращающуюся вокруг горизонтальной оси (рис. 2). На шкив радиуса 𝑟 наматывается нить, к которой через блок прикреплен подвес. Подвес представляет собой цилиндр с прорезью для закрепления на нити. Подвес при опускании движется вдоль вертикальной линейки, на которой отмечаются начальная и конечная точки движения. С помощью секундомера фиксируется точное время движения между этими точками. 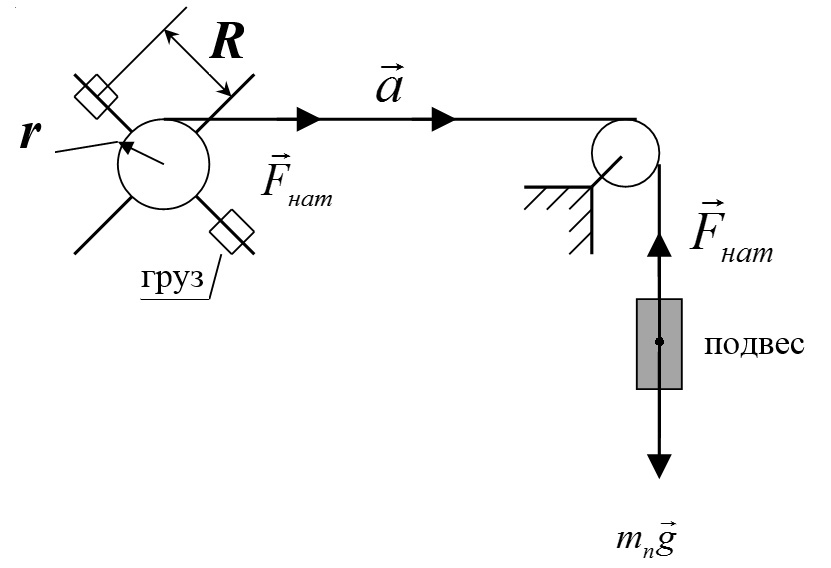 Шкив представляет собой два диска разных радиусов, закрепленных на одной оси. Это позволяет менять момент силы натяжения нити, наматывая нить либо на шкив одного радиуса, либо на шкив другого радиуса. Радиус большего шкива 17,5 мм, радиус меньшего шкива 9 мм. На данной фотографии нить намотана на больший шкив, следовательно, r = 0,0175 м. Нить перекинута через блок. К концу нити прикреплен стержень массой 25 грамм, на который надеваются цилиндрические подвесы. Плоский цилиндр имеет массу 50 грамм, высокий цилиндр имеет массу 150 грамм. Таким образом, на фотографии общая масса подвеса mn= 0,025 + 0,05 + 0,150 = 0,225 кг. Высота нахождения подвеса измеряется линейкой и определяется от уровня пола. На стержни маятника можно поместить грузы, на данной фотографии на стержнях закреплены два груза. Расстояние Rизмеряется от середины оси вращения до центра инерции груза Результаты эксперемента Определение собственного момента инерции крестовины и проверка основного закона динамики вращательного движения. В ходе эксперимента 3 раза проводилось измерение времени падения каждой из выбранных масс подвесов. Окончанием движения являлся момент удара подвеса о пол. Данные измерений и расчётов были занесены в Таблицу №1. Построен график зависимости углового ускорения маятника от момента силы натяжения нити. По графику определены момент силы трения и собственный момент инерции крестовины. Таблица №1 Определение собственного момента инерции крестовины I0 и проверка основного закона динамики вращательного движения.
r1= 17,5 мм = 0,0175 м Mнат=r*m(g-a) момент силы натяжения нити r2 = 0,9 мм = 0,009 м a=2h/t*2 ускорение с которым опускается подвес h = 0,9 м I= (Mнат-Мтр)/β момент инерции маятника Iгр=I- 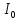 Iгр – момент инерции грузов на стержнях маятника Iгр – момент инерции грузов на стержнях маятникаМомент инерции маятника вместе с грузами 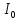 - момент инерции маятника без грузов( собственный моемент инерции маятника) - момент инерции маятника без грузов( собственный моемент инерции маятника)График зависимости углового ускорения маятника от момента силы натяжения нити ß = f(Mнат) 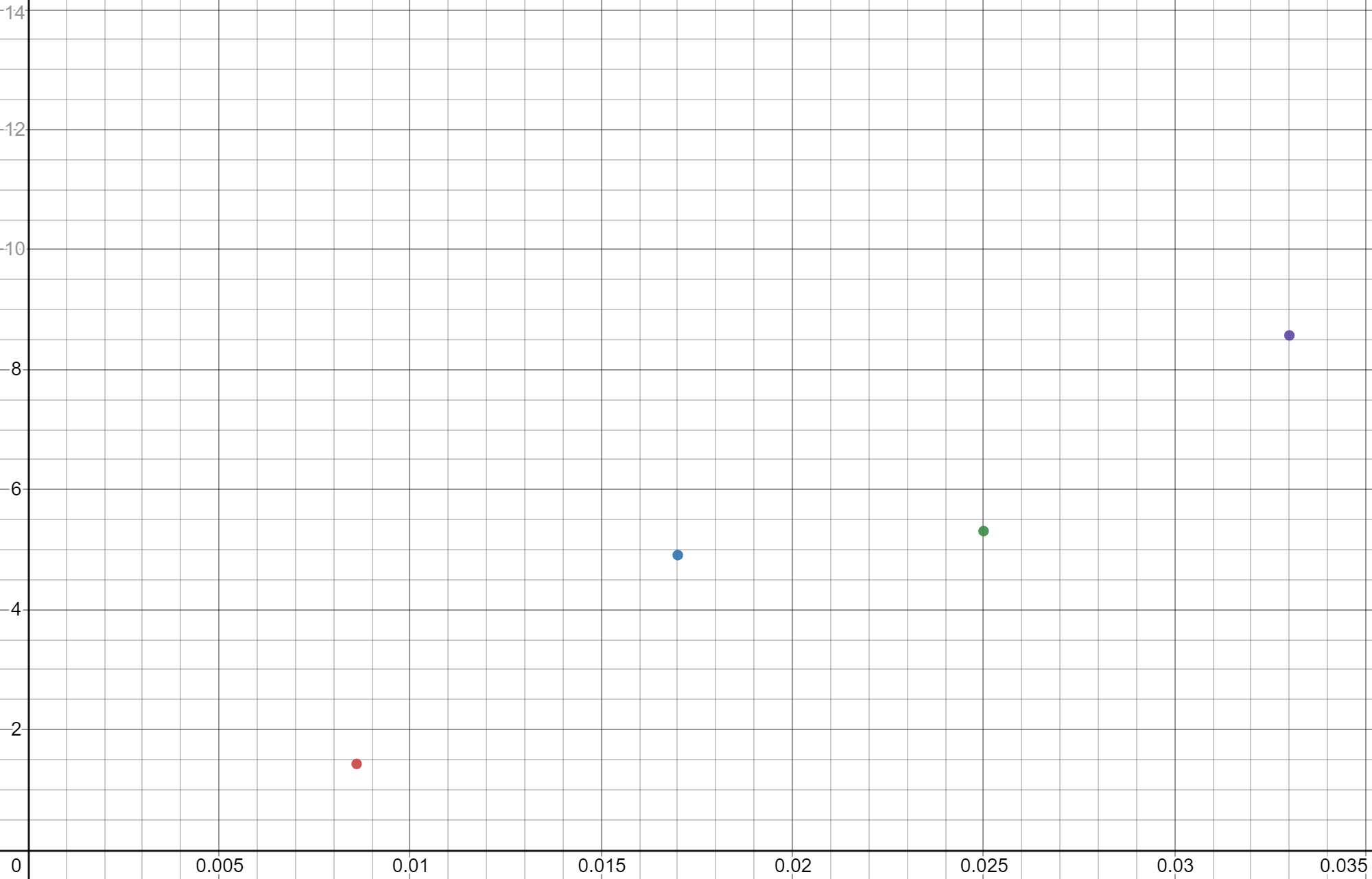 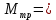 Вывод Я изучил законы динамики вращательного движения на основе маятника Обербека. Определил собственный момент инерции маятника крестовины. Исследовал зависимость момента инерции грузов на крестовине от расстояния до оси вращения. Контрольные вопросы Какое движение называется вращательным? Приведите примеры. В каких случаях размером тел при рассмотрении законов движения можно пренебречь? Ответ: Вращательное движение – это движение твёрдого тела, при котором все его точки, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, называемой осью вращения. Примеры: лопасти вертолёта, колесо, вращение планет вокруг своей оси. Размером тел можно пренебречь, когда размеры тела намного меньше, чем расстояние между двумя телами. Провести аналогию между параметрами кинематики и динамики поступательного и вращательного движения. Указать единицы измерения основных величин. Ответ: Законы поступательного и вращательного движений имеют много общего, большинство формул кинематики и динамики отличаются только обозначениями.
Эта аналогия справедлива не только в кинематике, но распространяется и на динамику. Роль массы т при вращении играет момент инерции I, а роль силы F - момент силы L. Основное уравнение динамики вращательного движения Iε=L записывается по аналогии с ma=F, кинетическая энергия вращения Iω²/2 по аналогии с mv²/2 и т. д. Дайте определение момента инерции твердого тела. Расскажите о теореме Штейнера. Ответ: Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений массы каждой точки тела на квадрат их расстояний от этой точки до рассматриваемой плоскости. Теорема Штейнера — момент инерции тела относительно произвольной оси вращения равен сумме момента инерции тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями. Вывести формулу основного закона динамики вращательного движения. Ответ: Динамика вращательного движения материальной точки. Рассмотрим ча-стицу массы m, вращающуюся вокруг токи О по окружности радиуса R, под действием результирующей силы F. В инерциальной системе отсчета справед-лив 2ой закон Ньютона. Запишем его применительно к произвольному моменту времени: F = m·a. Нормальная составляющая силы не способна вызвать враще-ния тела, поэтому рассмотрим только действие ее тангенциальной составляю-щей. В проекции на тангенциальное направление уравнение движения примет вид: Ft = m·at. Поскольку at = e·R, то Ft = m·e·R Умножив левую и правую части уравнения скалярно на R, получим: Ft·R= m·e·R2 M = I·e. Уравнение представ-ляет собой 2ой закон Ньютона (уравнение динамики) для вращательного движе-ния материальной точки. Ему можно придать векторный характер, учитывая, что наличие момента сил вызывает появление параллельного ему вектора угло-вого ускорения, направленного вдоль оси вращения M = I·e. Основной закон ди-намики материальной точки при вращательном движении можно сформулиро-вать следующим образом: произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку. Как в данной работе определить момент инерции маятника Обербека без грузов? Как в данной работе определить момент инерции маятника Обербека без грузов? 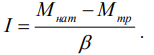 Если на крестовине маятника не находятся грузы, то формула позволяет определить собственный момент инерции маятника. Как в данной работе можно определить массу грузов на стержнях маятника Обербека? Для материальной точки момент инерции определяется как произведение массы на квадрат расстояния от оси вращения до центра масс тела, отсюда масса тела это отношение момента инерции к квадрату расстояния от оси вращения до центра масс тела: m=I/R^2. Как можно изменить момент инерции маятника Обербека? Ответ:Если известен момент инерции тела относительно оси, проходящей через центр инерции (центр масс) тела J0, то можно вычислить момент инерции тела относительно оси с помощью теоремы Штейнера. Момент инерции можно изменить с помощью изменения массы груза или же изменение расстояния до оси вращения. Если увеличить высоту опускания подвеса, то какие величины изменяются и как (момент инерции маятника, время опускания подвеса, кинетическая энергия системы маятник-груз, угловое ускорение маятника)? Ответ: Если увеличить высоту опускания подвеса, увеличится время его опускания. Угловое ускорение так же увеличится, поскольку из-за увеличения высоты увеличится ускорение, с которым опускается подвес. Кинетическая энергия увеличится. 1 |

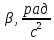
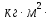
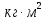
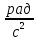 ]
]  ]
]