методические_разработки_к_лабораторным_занятиям_Восстановлен_Вос. Лабораторная работа 1 Исследование ряда случайных ошибок на закон нормального распределения
 Скачать 76.96 Kb. Скачать 76.96 Kb.
|
1 2 Обратный вес функции общего видаПусть дана функция 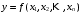 , где , где 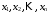 — независимо измеренные величины. Известны их веса — независимо измеренные величины. Известны их веса 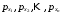 . .
и веса 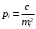 , получаем следующую формулу для вычисления обратного веса функции: , получаем следующую формулу для вычисления обратного веса функции: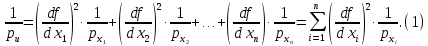 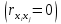 - условие. - условие.Если величины 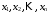 коррелированы, т.е. коэффициенты попарной корреляционной связи отличны от нуля, коррелированы, т.е. коэффициенты попарной корреляционной связи отличны от нуля, 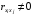 , то обратный вес функции вычисляется по формуле: , то обратный вес функции вычисляется по формуле: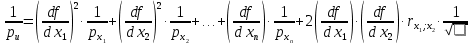 Положим, что при измерении величины х получены равноточные значения: a1, a2, …, ak b1,b2, …, bq c1, c2, …, cn Вероятнейшим, т.е. более надежным значением х является средняя арифметическая середина: 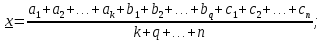 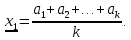 Используя формулу (2), получим: 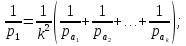 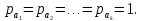 С учетом этих значений находим формулу общей арифметической середины: 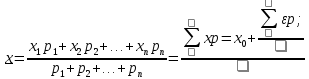 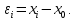 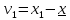 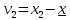 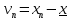 Умножив левые и правые части этих выражений на веса измерений и после сложения получим: 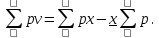 Подставив в это равенство вместо 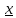 его значение, получим: его значение, получим: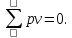 Сумма весов отклонений равна 0. Если отклонения 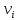 вычислены с использованием округленного значения, то сумма отклонений будет равна: вычислены с использованием округленного значения, то сумма отклонений будет равна: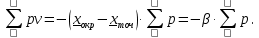 Если известны вероятнейшие ошибки 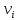 , то используем формулу Бесселя: , то используем формулу Бесселя: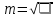 Средняя квадратическая ошибка среднего арифметического: 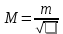 Надежность средней квадратической ошибки: 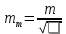 ; ;Надежность средней квадратической ошибки среднего арифметического: 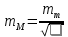 При большом числе n значение средней квадратической ошибки, вычисленное по формуле Бесселя и принятое при вычислении весов должна совпадать в пределах ошибки. Если 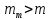 , то значит результат ненадежен и присутствуют систематические ошибки в измерениях. , то значит результат ненадежен и присутствуют систематические ошибки в измерениях.Практическое задание №1 Отметка Н точки получена по 7 нивелирным ходам, известны средние квадратические ошибки по каждому ходу mH. Вычислить вероятнейшее значение отметки и произвести оценку точности.
Веса вычисляем по формуле: 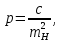 где с=10 где с=10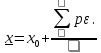 Вычисляем уклонения от среднего весового 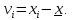 Контроль: 1. 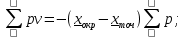 2. 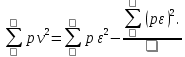 Найдем среднюю квадратическую ошибку m по формуле Бесселя. Вычислим среднюю квадратическую ошибку среднего арифметического М. Оценим надежность средней квадратической ошибки и средней квадратической ошибки среднего арифметического mm и mM. Ответ: записываем вероятнейшее значение отметки, оценим надежность результата измерения и наличие систематических ошибок. Практическое задание №2 Найти веса следующих функций: 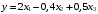 ; ;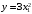 если 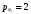 ; ; 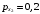 ; ; 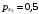 ; ; 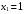 , , 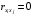 . .Лабораторная работа №6 Способ полигонов проф. В.В.Попова Цель работы: уравнять свободную сеть нивелирных ходов 4 класса, образующих три замкнутых полигона 1,2 и 3 (рис.1). Дано: подсчитаны невязки полигонов, дано количество штативов по звеньям. B II I C A D III Рис.1. Схема нивелирной сети Порядок выполнения работы: Вычерчивают схему уравнивания нивелирной сети. Около каждого хода, вне данного полигона, вычерчивают таблички, в которые будут вписываться поправки в процессе уравнивания. Вычисляют «красные числа», как отношение числа станций в звене к числу станций во всем полигоне (или отношение длины звена к периметру полигона). Контроль: сумма красных чисел для каждого полигона должна быть равна 1,00. Выбирают полигон с наибольшей невязкой, которую распределяют пропорционально красным числам, записывая поправки (со знаком невязки) в соответствующие внешние таблички. Контроль: сумма этих поправок должна быть равна невязке. На схеме распределенную невязку подчеркивают. Переходят ко второму полигону. В нем получена невязка и «выброшенная» из первого полигона поправка, следовательно, теперь надо распределять их алгебраическую сумму. Распределенную невязку и поправку на схеме подчеркивают. То же делают и в третьем полигоне схемы, заканчивая первый круг распределения невязок и подчеркивая при этом использованные числа. От полигона, в котором оказалась наибольшая невязка, начинают второй круг уравнивания, и так поступают до тех пор, пока все невязки не будут перенесены за границы полигонов. После этого в каждой табличке подсчитывают алгебраическую сумму поправок и записывают ее под двойной чертой. Вычисляют вероятнейшие поправки в превышения по каждому ходу, как разности алгебраических сумм, записанных во внутренней и внешней табличках у каждого хода (внутренняя поправка минус внешняя). Полученные таким путем поправки записывают в скобках внутри полигонов у соответствующих ходов. Контроль: сумма таких поправок по каждому полигону должна быть равна невязке, взятой с противоположным знаком. 1 2 |