методические_разработки_к_лабораторным_занятиям_Восстановлен_Вос. Лабораторная работа 1 Исследование ряда случайных ошибок на закон нормального распределения
 Скачать 76.96 Kb. Скачать 76.96 Kb.
|
1 2 Лабораторная работа №1 Исследование ряда случайных ошибок на закон нормального распределения Цель работы: исследовать данный ряд невязок на соответствие закону нормального распределения. Дано: дан статистический ряд случайных величин – угловые невязки 32 треугольников микротриангуляции. Требуется проверить гипотезу о том, подчиняется ли этот ряд невязок нормальному распределению случайных величин.
Общий порядок вычисления задачи: 1.Составить ранжированный ряд исходных величин, т.е. разместить случайные величины в порядке возрастания их абсолютных значений. 2.Вычислить эмпирические значения математического ожидания M(∆) и стандарта m. 3.Вычислить среднюю, вероятную и предельную ошибки, а также коэффициенты к1 и к2. 4.Вычислить величину χ2(критерий Пирсона). Оценить ряд случайных величин согласно критерию согласия Пирсона. 5.Вычислить начальные и центральные моменты, асимметрию и эксцесс. Оценить их значения по приближенному критерию. 6.Построить гистограмму, выравнивающую и теоретическую кривые распределения. 7.Сделать вывод о соответствии рассмотренного ряда случайных величин закону нормального распределения вероятности. Порядок вычисления: 1. Разместим невязки в порядке возрастания их абсолютных величин в таблице 1.
2. Вычислим эмпирические значения математического ожидания М(∆) и стандарта m: 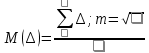 3. Вычислим ошибки: среднюю V, вероятную r и предельную ∆пред, а также коэффициенты к1 и к2. 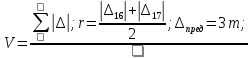 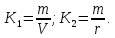 4. Вычислим величину χ2 (критерий Пирсона) в таблице 2, где невязки сгруппируем в 12 интервалов размером 0,5 m.
mi – количество ошибок в i-товом интервале. Значение Ф(t) – табличное (см. приложение А). Pi – разница между двумя соседними интервалами. В последнем столбце произведено вычисление χ2 (сумма данной графы). 5. Вычислим асимметрию As и эксцесс Е. Таблица 3. Вычисление данных для нахождения начальных моментов.
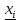 - середина интервала - середина интервалаПо данным таблицы 3 вычислим начальные моменты: 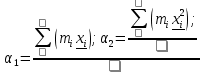 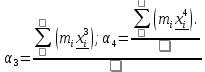 По вычисленным нами начальным моментам найдем центральные моменты второго, третьего и четвертого порядков. 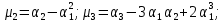 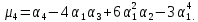 Рассчитаем значение асимметрии: 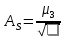 Рассчитаем значение эксцесса: 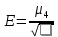 Найдем дисперсию асимметрии и эксцесса: 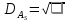 6. Построим гистограмму, выравнивающую и теоретическую кривые распределения. Таблица 4. Вычисление значений hi для построения диаграммы
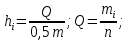 hi (max) = 10 Таблица 5. Вычисление ординат точек выравнивающей кривой.
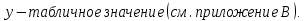 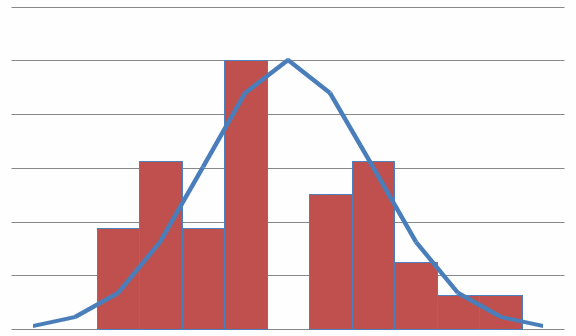 7. Сделать выводы о подчинении и неподчинении рассматриваемого ряда ошибок нормальному закону распределения. Для закона нормального распределения свойственно следующее: 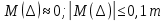 ; ;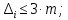 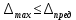 ; ;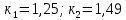 ; ;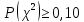 ; ;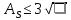 ; ; 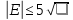 . .Лабораторная работа №2 Определение коэффициента корреляции и уравнения регрессии по опытным данным Цель: установить корреляционную связь между двумя величинами. Дано: даны абсолютные ошибки 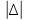 в превышениях, полученные при геометрическом нивелировании, и длины ходов D нивелирования. Требуется вычислить коэффициент корреляции величин в превышениях, полученные при геометрическом нивелировании, и длины ходов D нивелирования. Требуется вычислить коэффициент корреляции величин 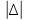 и D, коэффициент регрессии, оценить их точность и составить уравнение регрессии. и D, коэффициент регрессии, оценить их точность и составить уравнение регрессии.
Порядок вычисления: 1. Составить расчетную таблицу. 2. Вычислить коэффициент корреляции и уравнение регрессии. 3. Построить график зависимости величины ошибки ∆ от длины линии D. 4. Сделать вывод. Решение: 1. Составим таблицу:
2. Вычислим коэффициент корреляции: 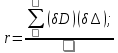 Найдем средние квадратические ошибки mD и m∆: 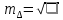 Определим надежность коэффициента корреляции (по таблице): см. приложение Г «Значение функции Z», приняв коэффициент корреляции в качестве аргумента. Найдем надежностный интервал для z: z - t·GZ ≤ z ≤ z + t·GZ По условию задачи t=2; 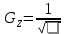 Минимально допустимое значение коэффициента корреляции вычислим по формуле: 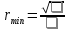 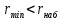 . .Составим уравнение регрессии: 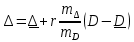 . .3. Построим график зависимости величины ошибки ∆ от длины линии D и прямую по уравнению регрессии. 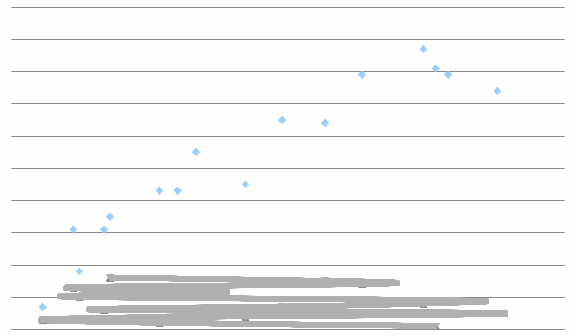 4. На основании полученных данных (по виду графика и неравенств) можно ли считать корреляционную связь установленной. Лабораторная работа №3 Обработка результатов равноточных измерений одной величины Цель работы: обработать данный ряд равноточных измерений. Дано: даны результаты равноточных измерений линии (м): 110, 338 381 394 387 385 379 393 386 382 389 Порядок выполнения работы: 1.Составить расчетную таблицу. 2. Провести контроль для суммы уклонений. 3. Вычислить и провести контроль величины 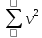 . .4. Вычислить среднюю квадратическую ошибку отдельного измерения. 5.Определить надежность средней квадратической ошибки отдельного результата измерений. 6.Вычислить среднюю квадратическую ошибку среднего арифметического. 7. Определить надежность средней квадратической ошибки среднего арифметического. Решение: Составим расчетную таблицу.
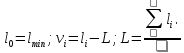 2. Контроль для суммы уклонений: 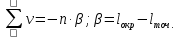 3. Вычислим и проведем контроль величины 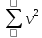 : :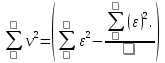 4.Вычислим среднюю квадратическую ошибку отдельного измерения по формуле Бесселя: 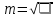 5.Определим надежность средней квадратической ошибки отдельного результата измерений: 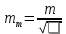 6.Вычислим среднюю квадратическую ошибку среднего арифметического: 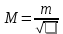 7.Определим надежность средней квадратической ошибки среднего арифметического: 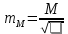 Лабораторная работа №4 Оценка точности по разностям двойных равноточных измерений Цель работы: оценить точность двойных равноточных измерений по их разностям. Дано: даны превышения между точками, определенные по черной и красной сторонам реек. Порядок выполнения работы: 1. Составить расчетную таблицу. 2. Провести контроль значения 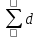 . .3. Вычислить среднюю квадратическую ошибку одного измерения и среднюю квадратическую ошибку арифметической середины. 4. Определить надежность средней квадратической ошибки отдельного результата измерений. 5. Определить надежность средней квадратической ошибки среднего арифметического. Решение: 1.Составим расчетную таблицу:
Вычислим значение остаточной систематической ошибки θ: 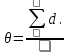 2. Контроль значения 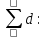 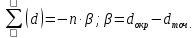 Критерием допустимости 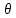 является неравенство: является неравенство: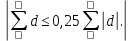 3. Вычислим среднюю квадратическую ошибку одного измерения 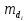 : :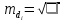 Вычислим среднюю квадратическую ошибку арифметической середины 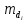 : : 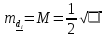 Следует заметить, что средние квадратические ошибки, полученные по разностям двойных измерений, обычно дают преуменьшенные результаты. 4. Определим надежность средней квадратической ошибки отдельного результата измерений: 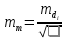 5. Определим надежность средней квадратической ошибки среднего арифметического: 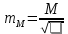 Лабораторная работа №5 «Обработка ряда неравноточных измерений» Теоретические пояснения 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

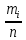
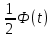
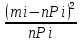
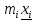
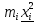
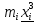
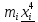
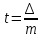
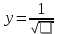
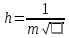
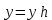
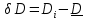
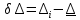
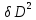
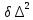
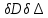
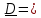
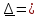
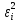
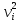
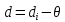 , мм
, мм