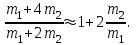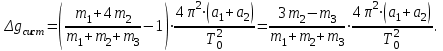Лабораторная. ЛР Физический маятник. Лабораторная работа 1 определение ускорения свободного падения с помощью физического маятника цель работы
 Скачать 1 Mb. Скачать 1 Mb.
|
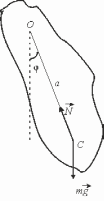
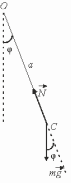
Лабораторная работа № 1 ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ ФИЗИЧЕСКОГО МАЯТНИКА Цель работы: определение ускорения свободного падения с помощью маятника-стержня, оценка точности измерения. Оборудование: установка, маятник - стержень. Теоретические замечания и вывод рабочей формулы Физическим маятником называется твердое тело произвольной формы, которое может качаться вокруг неподвижной горизонтальной оси под действием силы тяжести. Такой маятник изображен на рис.6, где т.О – точка, принадлежащая горизонтальной оси, т.С – центр масс маятника, φ – угол отклонения центра масс от вертикали, а – расстояние между т.О и т.С, 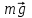 - сила тяжести. - сила тяжести.
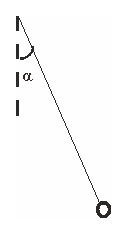
Математическим маятником называется маятник, вся масса которого практически сосредоточена в одной точке - в центре масс маятника. Т.е. он является частным случаем физического маятника. Его можно представить как небольшой шарик, подвешенный на длинной нити (рис.7).
Для измерения ускорения свободного падения  можно использовать оба эти маятника. Но так как нить математического маятника должны быть очень длинной и нерастяжимой, то в лабораторных условиях более точным и удобным является измерение можно использовать оба эти маятника. Но так как нить математического маятника должны быть очень длинной и нерастяжимой, то в лабораторных условиях более точным и удобным является измерение 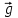 с помощью физического маятника. с помощью физического маятника. Рассмотрим колебания физического маятника, представленного в виде маятника-стержня (рис. 8). На тело действуют сила тяжести 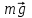 , сила реакции опоры , сила реакции опоры 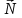 и сила сопротивления воздуха, действием которой пренебрегаем. и сила сопротивления воздуха, действием которой пренебрегаем. В соответствии с основным уравнением вращательного движения тел проекцию общего вращающего момента 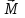 относительно оси можно связать с угловым ускорением относительно оси можно связать с угловым ускорением 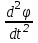 соотношением соотношением
где I – момент инерции физического маятника относительно оси вращения.
Общий вращающий момент 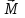 складывается из моментов сил, действующих на маятник: силы тяжести, силы реакции опоры. складывается из моментов сил, действующих на маятник: силы тяжести, силы реакции опоры. Момент, создаваемый силой тяжести 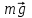 , можно записать в виде , можно записать в виде
где а— расстояние от оси вращения до центра тяжести тела φ – угол отклонения маятника от положения равновесия. Если этот угол мал (до 100), то sin φ ≈ φ. Момент силы реакции опоры
С учетом всего этого уравнение (19) можно преобразовать к виду
или
Это дифференциальное уравнение, описывающее гармонические колебания. Его решением является периодическая функция
в которой величина φ0 представляет максимальный угол отклонения маятника от положения равновесия, α0 — начальную фазу колебаний. (Значения φ0 и α0 определяются из начальных условий). Система будет возвращаться в исходное состояние через такое время Т,за которое аргумент под знаком синуса изменится на величину
Из равенства (23) получим выражение для периода колебаний физического маятника
Круговая частота колебаний физического маятника соответственно равна 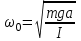 . .Необходимо отметить, что соотношения (23)—(24) справедливы лишь для малых углов отклонения (5 – 100). В противном случае период колебания будет зависеть от угла φ. Вывод рабочей формулы По теореме Штейнера-Гюйгенса момент инерции тела Iможно представить следующим образом: I = I0 + ma2, где I0 — момент инерции тела относительно оси, параллельной оси вращения и проходящей через центр тяжести тела. В этом случае формула (6) примет вид
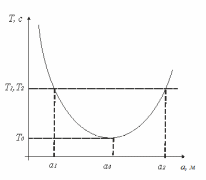
Увеличение априводит, с одной стороны, к увеличению момента силы, возвращающей маятник в положение равновесия, благодаря чему период колебания стремится уменьшиться, и, с другой стороны – к росту момента инерции системы I= I0 + ma2, который наоборот способствует увеличению периода колебаний. Характерная зависимость T = f(a) для физического маятника-стержня приведена на рис. 9.
При достаточно малых значениях расстояния а, когда выполняется условие 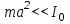 из равенства (25) имеем из равенства (25) имеем
Следовательно, с увеличением значения азначение периода колебания Тбудет уменьшаться. Ход кривой качественно можно объяснить следующим образом: подвесу маятника в центре тяжести (а = 0) должен соответствовать бесконечно большой период колебаний, так как в этом случае величина возвращающего момента 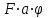 равна нулю. Реально это означает, что колебания маятника в этом случае отсутствуют. равна нулю. Реально это означает, что колебания маятника в этом случае отсутствуют.При небольших значениях а рост момента инерции не оказывает решающего влияния на изменение периода колебаний, и наблюдается спад кривой. Но, начиная с а = ао, рост момента инерции оказывает большее влияние на период колебаний, чем влияние возвращающего момента М,и имеет место подъем кривой При сравнительно больших значениях аимеет место неравенство 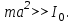 Тогда из равенства (26) получим Тогда из равенства (26) получим
Очевидно, точка аосоответствует положению, когда рост момента инерции и вращающего момента оказывают одинаковые противоположные действия. Один и тот же период колебаний может быть у маятника при различных расстояниях а от центра тяжести до точки подвеса. Если маятник подвешен сначала на расстоянии а1от центра тяжести, а затем на расстоянии а2 то соответствующие периоды колебаний будут иметь вид
Из системы (28), исключивI0 можно определить ускорение свободного падения g:
В частном случае, когда периоды колебаний, соответствующие точкам подвеса а1и а2совпадают, то есть Т1=Т2=Т0 (см. рис. 9), соотношение (29) упрощается и сводится к виду:
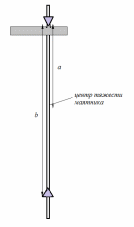
Ускорение свободного падения можно определить из экспериментально снятой кривой зависимости Т=f(а). Для этого на построенном графике надо найти такие точки a1 и а2, которым соответствует один и тот же период колебаний Т0, а для вычисления gвоспользоваться выражением (30). Однако, эта формула применима в случае, когда маятник представляет собой стержень, не имеющий дополнительных деталей. При наличии в конструкции маятника дополнительных частей формула для расчета ускорения свободного падения будет иметь другой вид. Общий вид установки, используемой в работе, представлен на рис. 10. Физическим маятником служит металлический стержень 1 с нанесенными на нем расстоянии 1 см друг от друга делениями. Вдоль стержня могут перемещаться две треугольные призмы 2,которые необходимо закреплять на стержне симметрично относительно его середины во избежание смещения центра тяжести. На конце горизонтальной части 3 кронштейна 4 имеются небольшие углубления, в которые упирается основание верхней призмы при колебаниях маятника. Установка позволяет считать периоды колебаний и время в автоматическом режиме, для этого предусмотрены кнопки «Сброс» и «Стоп». При выводе рабочей формулы для определения ускорения силы тяжести с помощью данной установки необходимо учитывать массы и моменты инерции опорных призм относительно оси качания маятника. В этом случае выражение для периода колебаний маятника-стержня примет вид
где m1, m2, m3– массы стержня, нижней и верхней призм соответственно; I01— момент инерции стержня относительно оси, проходящей через центр тяжести стержня и параллельной оси качания маятника; I02 – момент инерции верхней призмы относительно оси качания маятника; b – расстояние от центра тяжести нижней призмы до точки подвеса маятника (рис.11).
Записав соотношение (31) для случаев a1, b1, T1 и a2, b2, T2 и исключив из уравнений величину 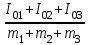 , при T1=T2=T0 имеем , при T1=T2=T0 имеем
Поскольку можно положить b1 ≈ 2a1, b2 ≈ 2a2, то окончательно получим рабочую формулу для определения ускорения свободного падения с помощью маятника стержня
Если не учитывать наличие опорных призм и пользоваться более простой формулой (32), то это приведет к появлению систематической погрешности. Величину этой погрешности можно оценить по формуле, которая получена вычитанием выражения (32) из выражения (33):
Порядок выполнения работы Измерить длину стержня и определить положение центра тяжести стержня. Установить призмы симметрично у концов стержня. Измерить с точностью до 1 мм расстояние aмежду точкой подвеса и центром тяжести стержня. Подвесить стержень, за одну из призм, поместив ее в верхней части установки. Вывести маятник-стержень из положения равновесия на угол не более 150, проследив, чтобы возникшие в результате колебания происходили в одной плоскости. Нажать на установке кнопку «Пуск». После этого встроенные секундомер и счетчик периодов начнут отсчет времени t и количества периодов N. Прекратить отсчет нажатием кнопки «Стоп» при достижении количества периодов N = 20. Занести в таблицу 1 значения a и соответствующие ему значения t и N. Вычислить период колебаний Т и занести в таблицу 1. Переместить призмы друг к другу симметрично на 1 см с каждой стороны и повторить измерение t, N и вычислить T. Результаты занести в таблицу 1. Продолжая перемещать призмы по 1 см с каждой стороны к центру тяжести, проводить аналогичные измерения и вычисления до тех пор, пока призмы не сблизятся настолько, что период колебаний резко возрастет, и колебаний практически прекратятся. По полученным данным построить график зависимости периода колебаний T от расстояния a. Таблица 1
На графике найти несколько точек со значениями периода T0, каждому из которых соответствуют по 2 значения расстояния а1 и а2. Найденные значения занести в таблицу 2. Рассчитать значение ускорения свободного падения g по формуле (33). Результаты вычислений занести в таблицу 2. Таблица 2
Проанализировать результат: сравнить полученное значение с известным значением gтабл для данной местности и объяснить причины отличия от него. Сравнение проводить по формуле 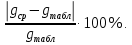 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

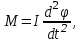
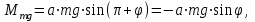
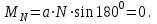
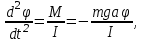
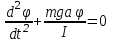
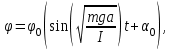
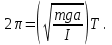
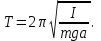
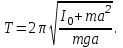
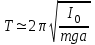 a-1/.2
a-1/.2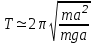 a1/.2
a1/.2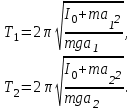
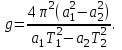
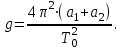
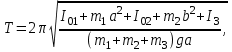

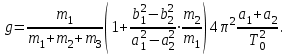
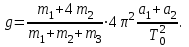
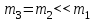 и
и