Лабораторная работа 1 Основы измерений и обработки результатов
 Скачать 5.67 Mb. Скачать 5.67 Mb.
|
Цель работы: исследование удара, изучение законов сохранения импульса и механической энергии при ударе.Основные теоретические положения Удар – совокупность явлений, возникающих при кратковременном приложении к телу внешних сил, например, при взаимодействии с другим движущимся относительно него телом, связанных со значительным изменением его скорости за очень короткий промежуток времени. Абсолютно неупругим называют такой удар, после которого скорости обоих соударяющихся тел оказываются одинаковыми. Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает – кинетическая энергия тел полностью или частично превращается во внутреннюю энергию. При абсолютно неупругом ударе выполняется лишь закон сохранения импульса и имеет место закон сохранения суммарной энергии различных видов – механической и внутренней. 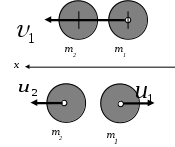 А А Рис. 5.1. Упругое соударение шаров бсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии. Потенциальная энергия упругой деформации вновь переходит в кинетическую энергию, и тела разлетаются со скоростями, величина которых определяется двумя условиями – сохранением полной энергии и сохранением полного импульса системы тел. Рассмотрим центральный абсолютно упругий удар двух шаров. Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры. Пусть шары массами Выберем ось x в направлении движения шаров, тогда в проекции на эту ось закон сохранения импульса принимает вид На основании закона сохранения энергии имеем Сгруппировав слагаемые с одинаковыми индексами, перепишем эти равенства в виде Поделив (5.4) на (5.3), получим или Таким образом, при абсолютно упругом ударе относительная скорость шаров остается неизменной величиной. Решая совместно уравнения (5.5) и (5.3), получим Рассмотрим два частных случая. 1. Сумма импульсов обоих шаров до ударов равна нулю, то есть тогда отсюда, применяя (5.9), находим: 2. Один шар до удара покоится 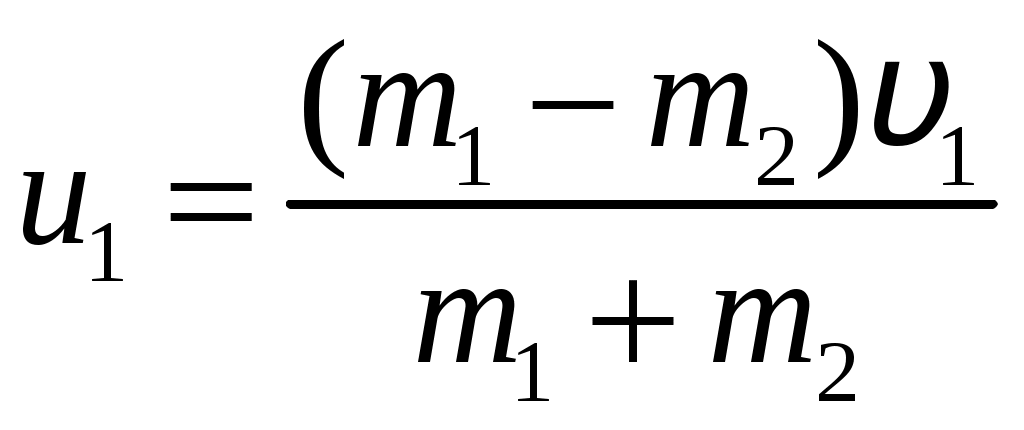 , , После удара второй шар двинется в ту же сторону, куда двигался первый до удара. Скорость а) Если б) Если в) Массы шаров одинаковы где Из (5.10) следует, что 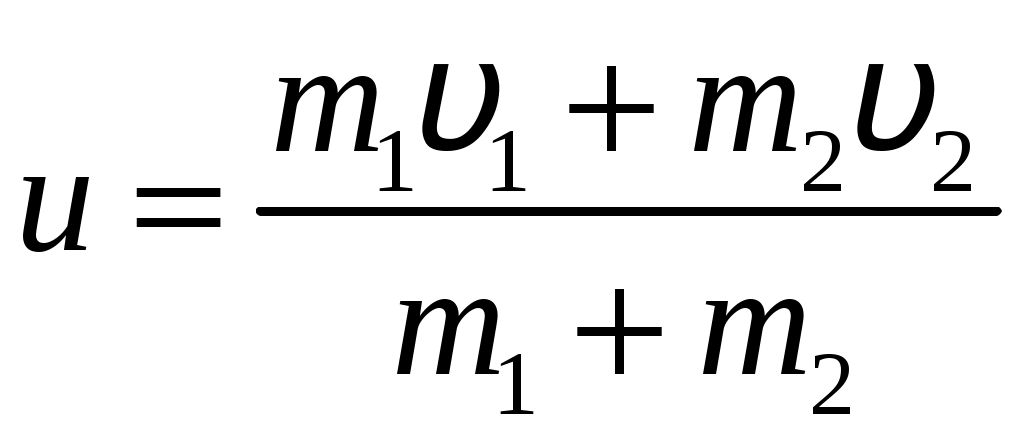 . (5.11) . (5.11)В частном случае, когда массы шаров равны, В случае нецентрального удара можно разложить скорости шаров на составляющие Так как Для четырех неизвестных компонент скорости Соответствующие слагаемые в (5.14) сократятся, и для нормальных составляющих мы получим два уравнения: 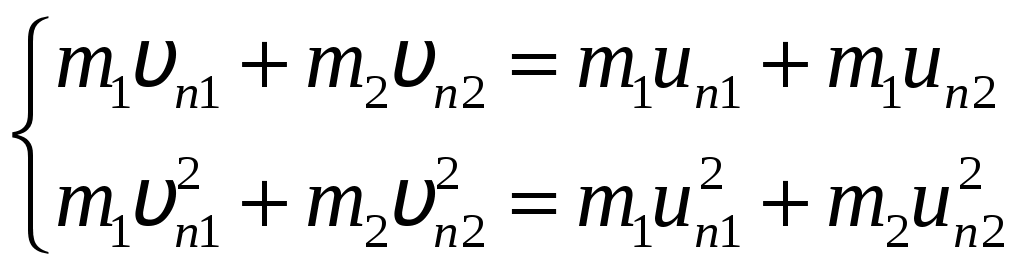 . (5.15) . (5.15)Э 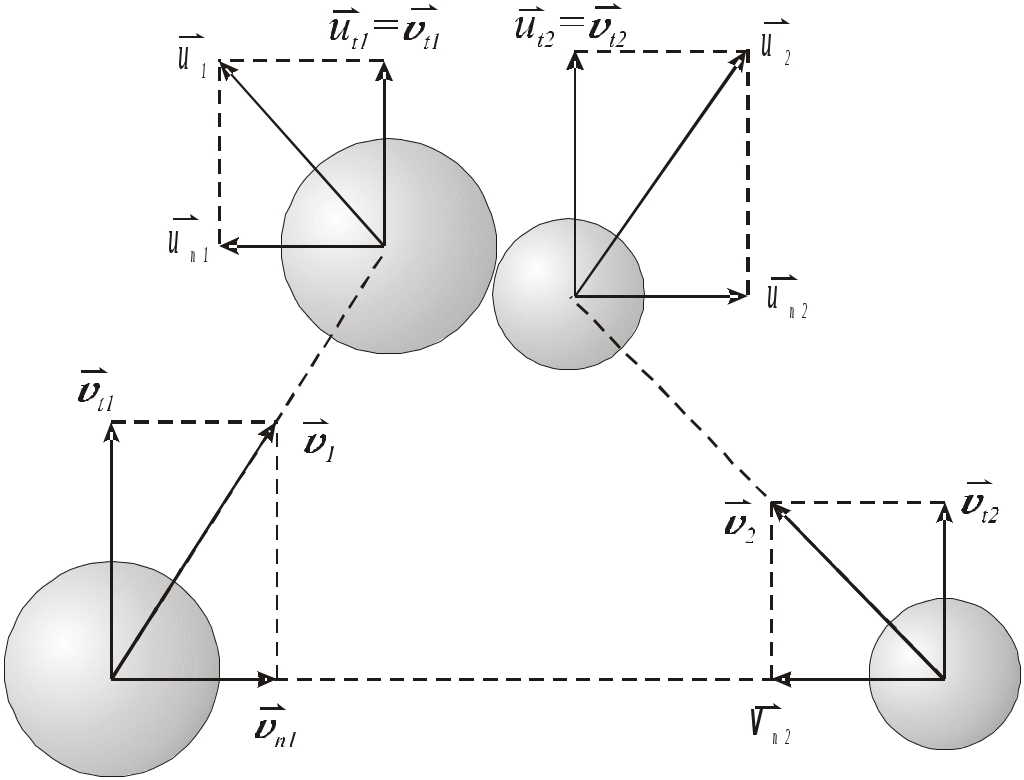 ти уравнения совершенно аналогичны тем, которые были получены для центрального удара. Таким образом, при нецентральном абсолютно упругом ударе гладких шаров нормальные составляющие скоростей ведут себя так же, как при центральном ударе; тангенциальные же составляющие не изменяются. ти уравнения совершенно аналогичны тем, которые были получены для центрального удара. Таким образом, при нецентральном абсолютно упругом ударе гладких шаров нормальные составляющие скоростей ведут себя так же, как при центральном ударе; тангенциальные же составляющие не изменяются.В Рис. 5.2. Соударение шаров случае не абсолютно упругого удара часть кинетической энергии шаров при соударении переходит в энергию остаточной деформации. Тогда Неупругий удар сопровождается остаточной деформацией. Если пренебречь всякого рода сопротивлениями, закон сохранения энергии для удара двух одинаковых шаров запишется так где Экспериментальная установка и методика измерений С  хема лабораторной установки показана на рис. 5.3. К штативу 3 на бифилярных подвесах 4 и 5 прикреплены два шара 1 и 2. Бифилярный подвес используется для исключения вращения шаров. Шарики подвешены так, что их центры находятся на одном уровне, а сами шарики соприкасаются. хема лабораторной установки показана на рис. 5.3. К штативу 3 на бифилярных подвесах 4 и 5 прикреплены два шара 1 и 2. Бифилярный подвес используется для исключения вращения шаров. Шарики подвешены так, что их центры находятся на одном уровне, а сами шарики соприкасаются.На столе под шариками в плоскости их колебания размещена линейка 6 (рис. 5.3). О Рис. 5.3. Схема установки тведем один из шаров (например, большой) на некоторый угол θ (рис. 5,4) и отпустим без начальной скорости. Отклоненный шар будет двигаться вниз, разгоняясь, при этом его потенциальная энергия будет переходить в кинетическую. Пусть столкновение со вторым шаром происходит в тот момент, когда подвес первого шара становится вертикально. Если удар происходит достаточно быстро, так, что нити во время удара не успевают отклониться на заметный угол, то в направлении горизонтальной оси x не возникает внешних сил и выполняется закон сохранения импульса в проекции на эту ось П  о закону сохранения механической энергии (рис. 5.3) о закону сохранения механической энергии (рис. 5.3)г Рис. 5.4. Соударение шаров де При достаточно малых отклонениях (≤ 5°) Тогда с учетом приближенного равенства  . (5.19) . (5.19)Из соотношений (5.18) и (5.19) получаем 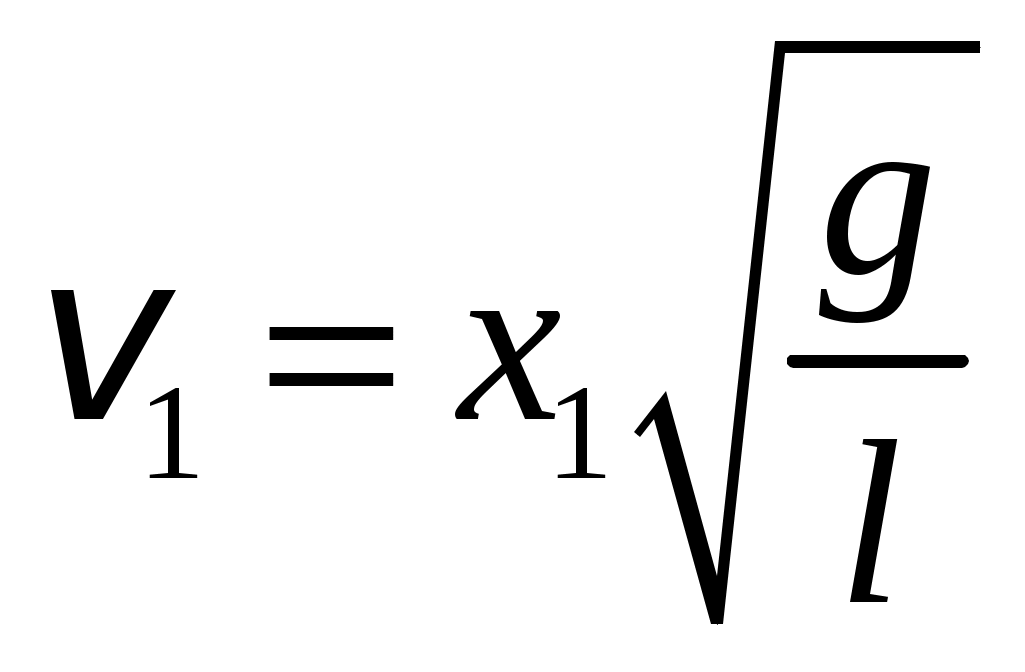 . (5.20) . (5.20)После удара оба шарика отклонятся от положения равновесия на расстояния 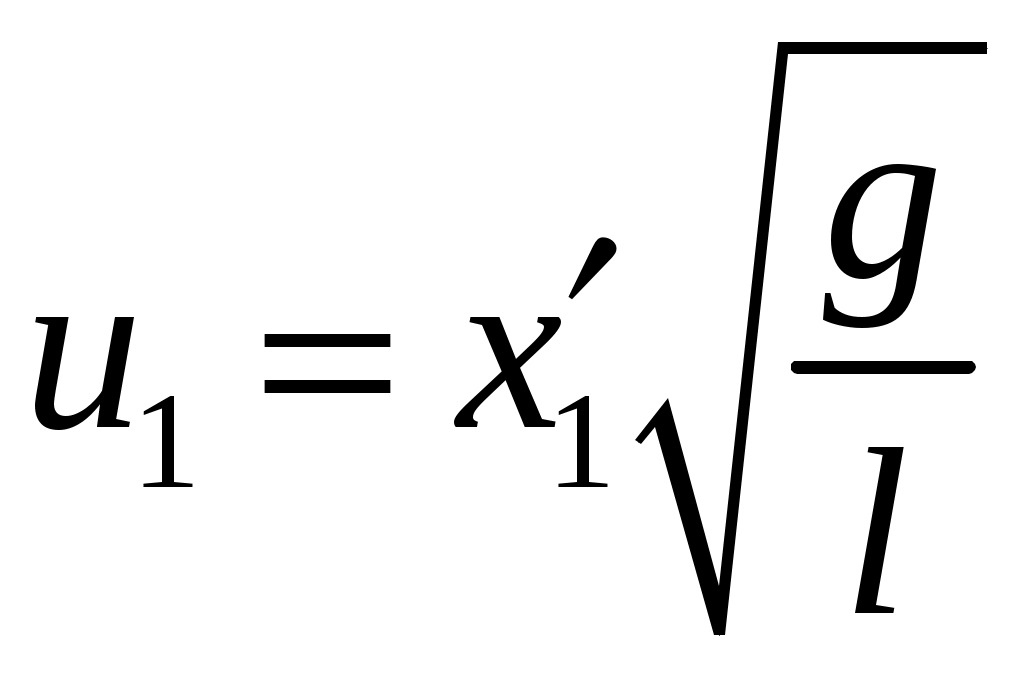 , , 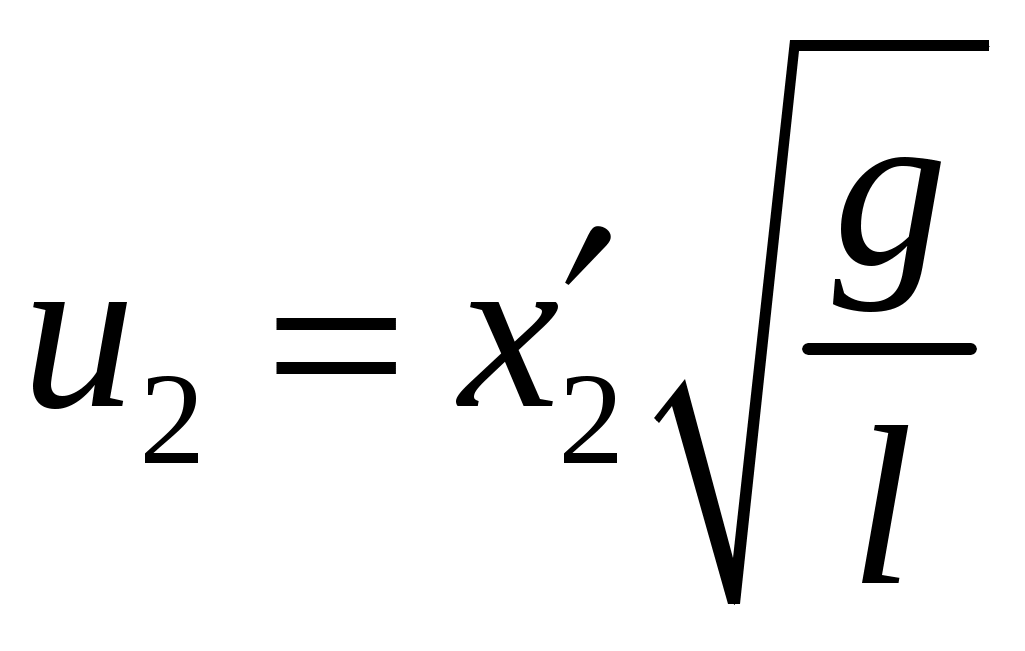 . (5.21) . (5.21)Подставляя эти соотношения в закон сохранения импульса (5.17), после несложных преобразований получаем 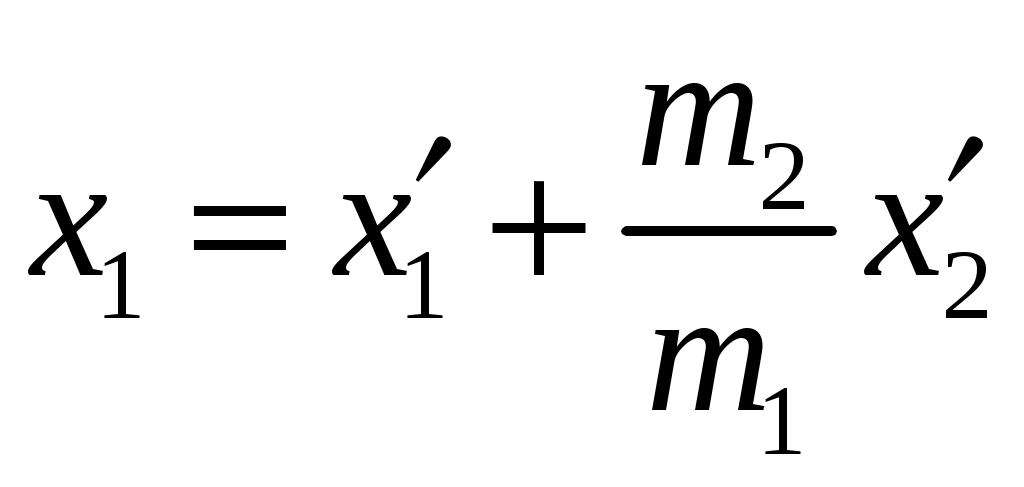 (5.22) (5.22)Задание 1. Проверка соотношения (5.22). Экспериментально проводится в следующей последовательности: большой шарик отклоняется из положения равновесия на фиксированную величину x1, и после соударения по шкалам визуально определяются отклонения шаров Если в эксперименте отклоняется шарик меньшей массы, то при ударе о шар большей массы он отскакивает в противоположную сторону. В этом случае 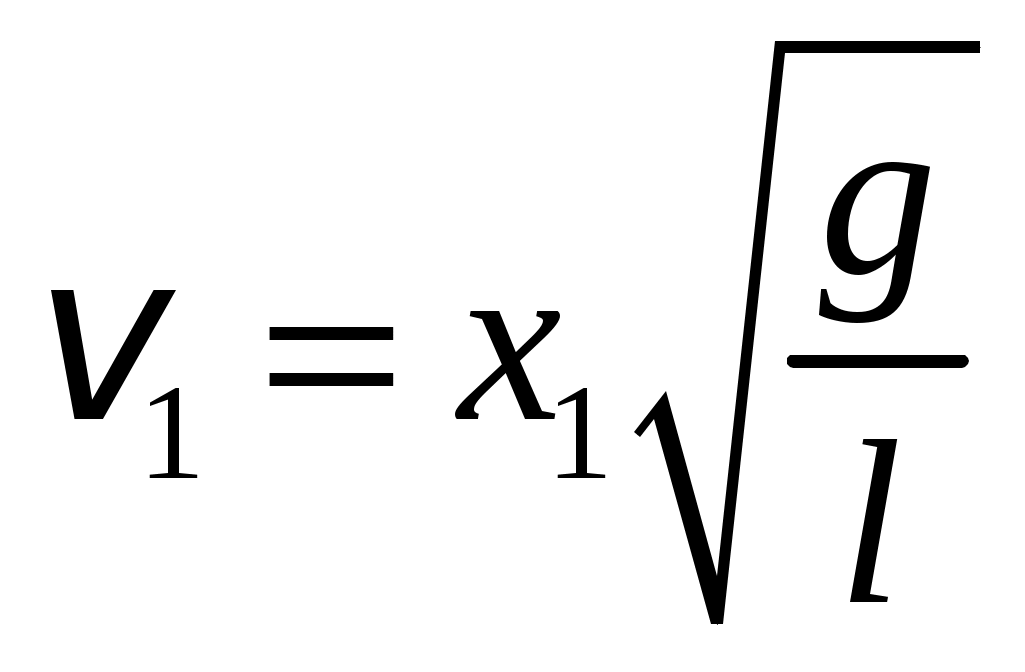 , , 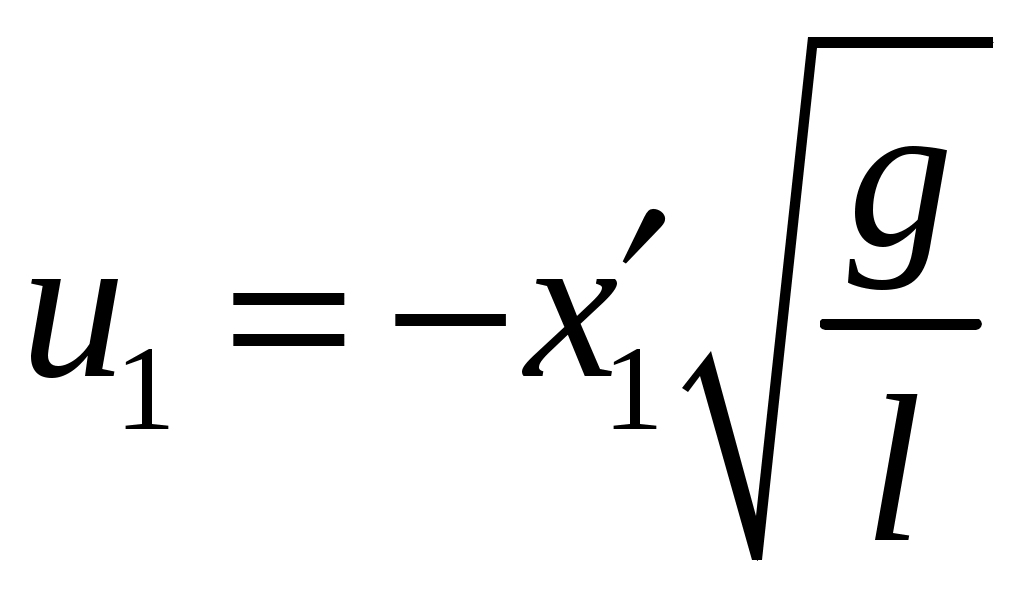 , , 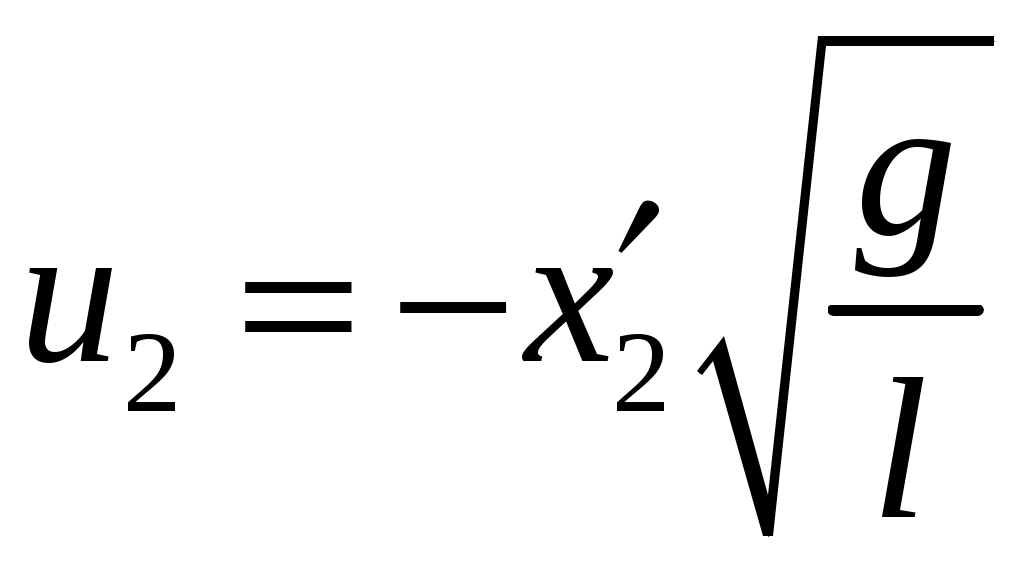 . .После подстановки в закон сохранения импульса получим 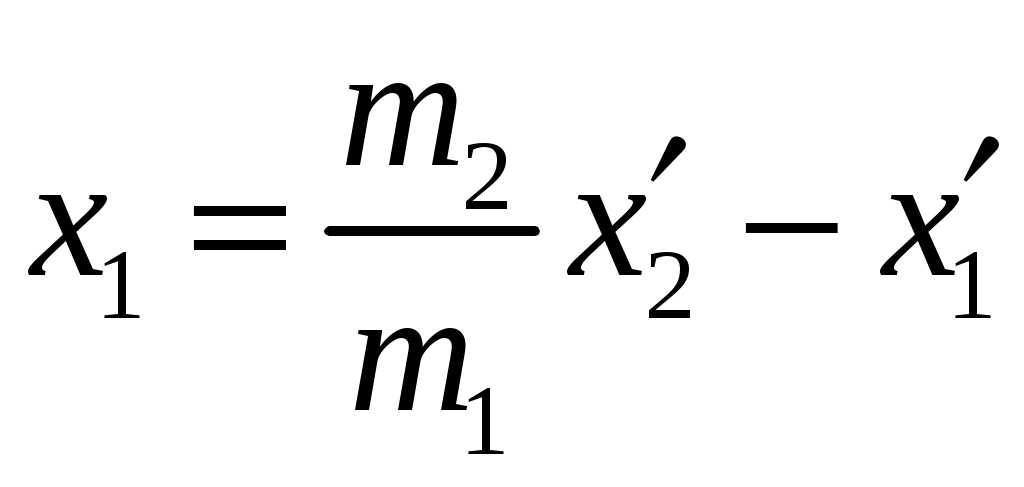 . (5.23) . (5.23)Задание 2. Проверка соотношения (5.23). Эксперимент проводят точно так же, как и в предыдущем случае. Задание 3. Реальные тела являются промежуточными между телами абсолютно упругими и абсолютно неупругими, поэтому при соударении реальных тел всегда имеют место и упругие, и остаточные деформации. Коэффициент 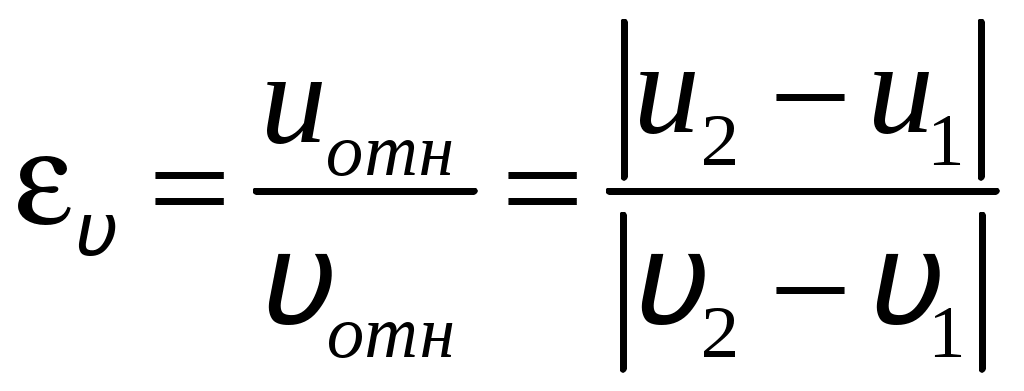 . (5.24) . (5.24)В случае первоначального отклонения большего шара формула (5.24) с учетом (5.20) и (5.21) преобразуется к виду 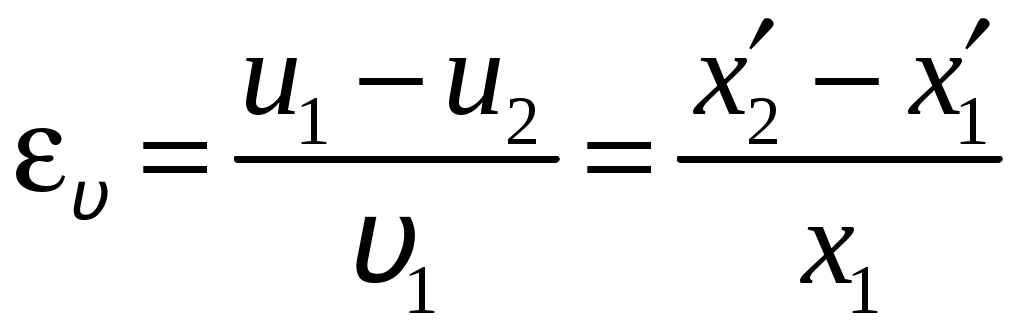 . (5.25) . (5.25)Для абсолютно упругого удара В случае первоначального отклонения меньшего шара формула (5.25) с учетом (5.21) и (5.22) преобразуется к виду 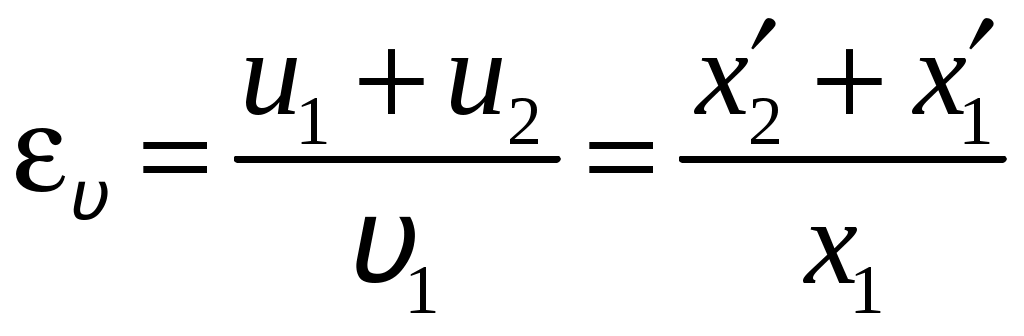 . (5.26) . (5.26)Кроме коэффициента восстановления скорости соударение тел характеризуется коэффициентом 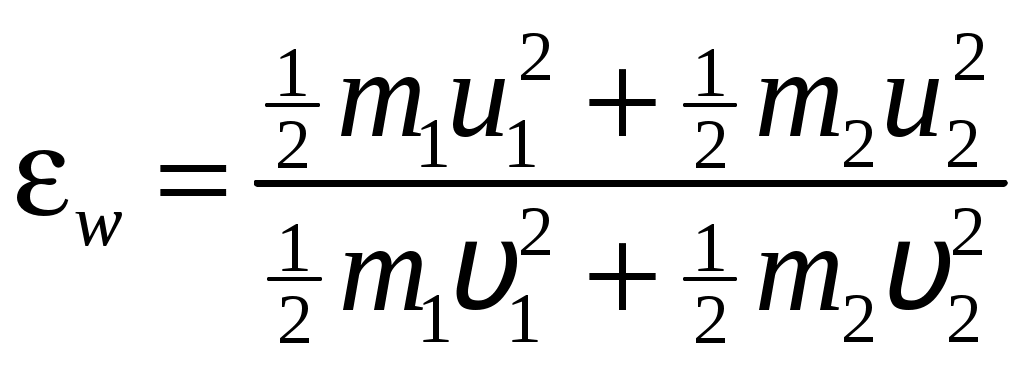 . (5.27) . (5.27)Учитывая, что скорость второго шара до удара 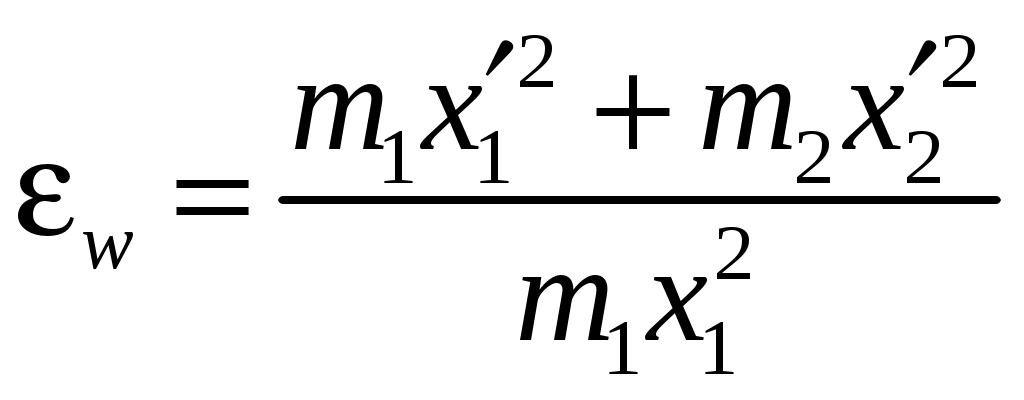 . (5.28) . (5.28)Обработка результатов эксперимента Найдите средние значения величины отскока шаров после удара Используя средние значения По методике расчета случайных погрешностей прямых измерений найдите погрешности измерения отклонений Найдите погрешность определения а) для случая отклонения большего шара 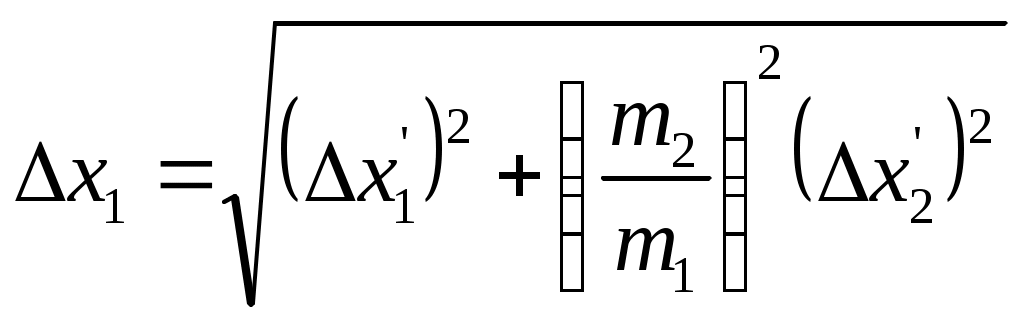 ; (5.29) ; (5.29)б) для случая отклонения меньшего шара 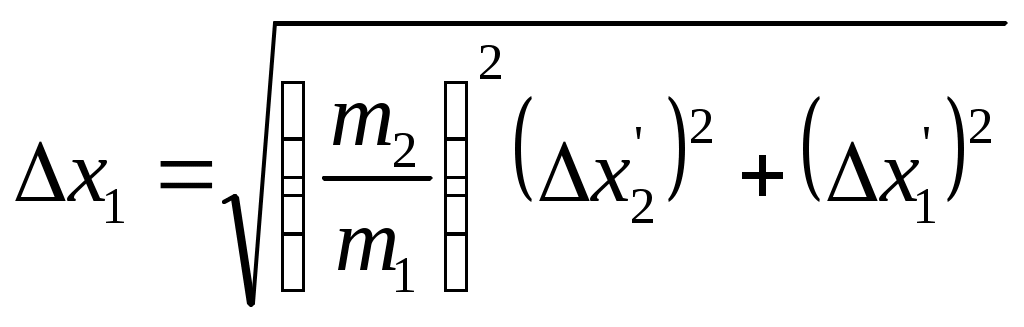 . (5.30) . (5.30)5. Сравните полученное из эксперимента значение x1 с учетом его приборной погрешности, то есть 6. Погрешность определения коэффициента восстановления 7. Погрешность определения коэффициента восстановления 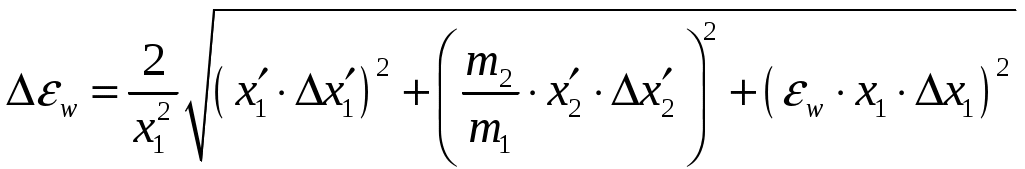 . (5.32) . (5.32)Л Х абораторная работа 6 |
