Лабораторная работа 1 Основы измерений и обработки результатов
 Скачать 5.67 Mb. Скачать 5.67 Mb.
|
|
ТЕПЛОЕМКОСТЬ ЖИДКОСТИ Цель работы: изучение классической теории теплоемкости, экспериментальное определение теплоемкости жидкости калориметрическим методом. Основные теоретические положения К 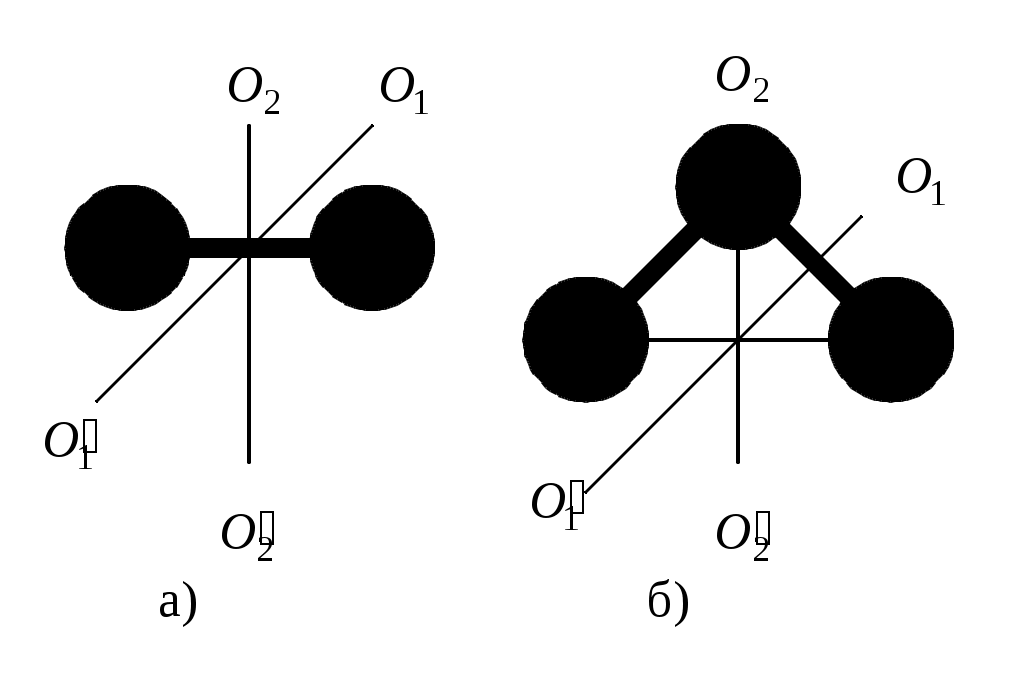 Рис. 8.1. Двух (а) и трехатомная (б) молекула оличество независимых координат, характеризующих положение материального объекта в пространстве, называется числом его степеней свободы. Молекулу одноатомного идеального газа можно рассматривать как материальную точку, так как ее масса сосредоточена в ядре малого размера. Такая молекула (атом) имеет три степени свободы, то есть для описания ее поступательного движения требуется три независимых координаты. Для того чтобы охарактеризовать положение в пространстве двухатомной молекулы, состоящей из жестко связанных атомов, необходимо задать пять независимых координат. Из них три служат для описания ее поступательного движения, а две характеризуют вращательное движение вокруг осей Одним из основных положений классической молекулярно-кинетической теории является закон равномерного распределения энергии по степеням свободы: на каждую поступательную, а также вращательную степень свободы газовой молекулы приходится одинаковая энергия, равная Если считать, что в газах, жидкостях и твердых телах молекулы колеблются независимо друг от друга, то на три колебательные степени свободы каждой молекулы приходится энергия Полная внутренняя энергия одного моля такой системы молекул равна: где Молярной теплоемкостью называется количество энергии, поглощаемой одним молем вещества при нагревании на 1 К, то есть Это закон Дюлонга и Пти: молярные теплоемкости химически простых веществ одинаковы и не зависят от температуры. Закон Дюлонга и Пти хорошо выполняется при комнатной температур. Для более низкой температуры наблюдаются отклонения, связанные с тем, что энергию колебательного движения молекул нельзя вычислять на основании закона о равнораспределении энергии по степеням свободы. Теплоемкость в этой области уменьшается, стремясь к нулю при Качественное согласие с результатами эксперимента было достигнуто в теории Эйнштейна, в которой предполагалось, что молекула представляет собой не классический, а квантово-механический гармонический осциллятор, средняя энергия которого определяется соотношением: 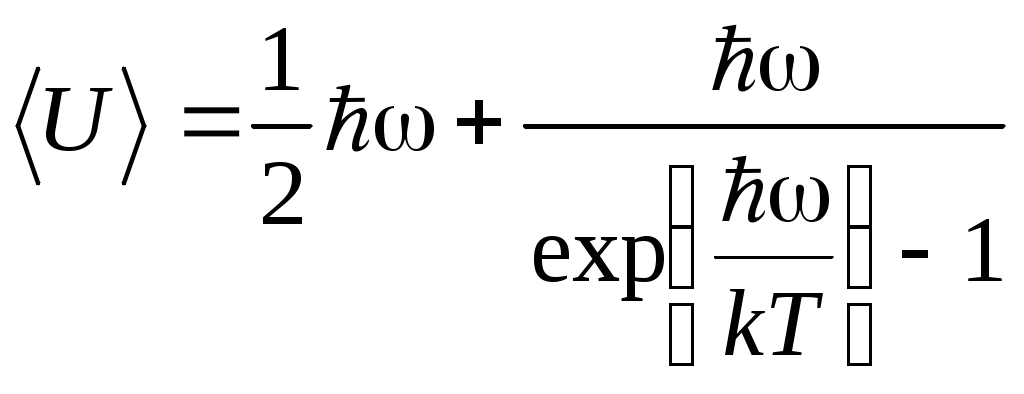 , (8.4) , (8.4)где 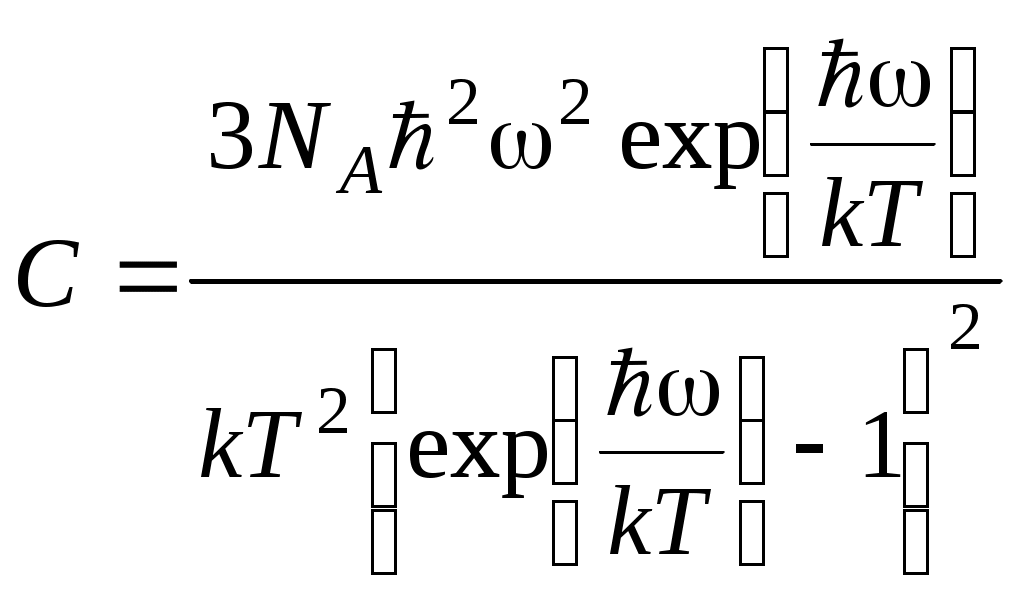 . (8.5) . (8.5)При высоких температурах 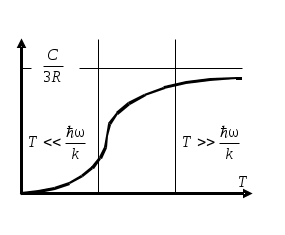 Выражение (8.6) при Т Рис. 8.2. Зависимость теплоемкости от температуры еория Эйнштейна лишь качественно совпадает с результатами эксперимента в области низких температур. Строгая теория, описывающая Описание экспериментальной установки Калориметр представляет собой сосуд 1, стенки которого теплоизолированы между собой с помощью прокладки из теплоизолирующего материала 2, а также от окружающей среды крышкой 3. В сосуд помещается исследуемое вещество 4 (в нашем случае жидкость), температура которой определяется термометром 5. Нагревание жидкости осуществляется нагревателем 6, мощность которого определяется по току, регистрируемому стрелочным прибором (рис. 8.3). Для изменения тока применяется реостат R. Для улучшения условий теплообмена жидкость в эксперименте перемешивается специальной мешалкой 7, которая вращается электродвигателем. Т 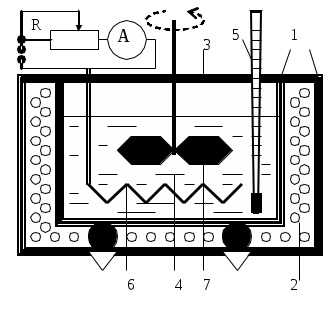 еплота нагревателя У Рис. 8.3. Экспериментальная установка равнение теплового баланса записывается так Теплоемкость исследуемой жидкости в интервале температур от Поэтому С учетом этого уравнение теплового баланса записывается в виде Если бы тепловые потери отсутствовали, Пусть Тогда из формулы (8.11) получим Отсюда теплоемкость жидкости в калориметре 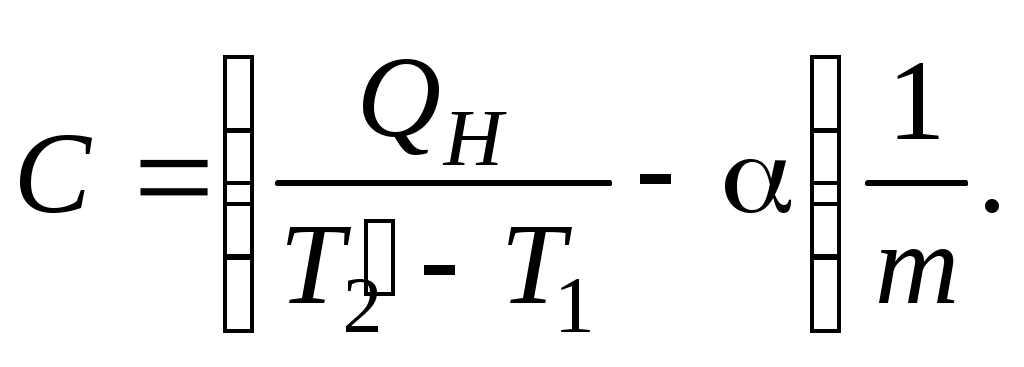 (8.13) (8.13)Т 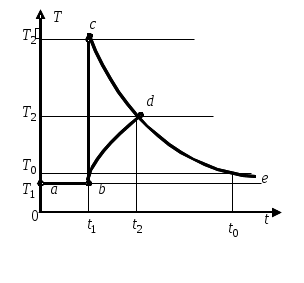 аким образом, для определения теплоемкости исследуемой жидкости необходимо знать температуру Р Рис. 8.4. Диаграмма нагревания жидкости в калориметре ассмотрим процесс нагревания жидкости в калориметре. До включения нагревателя температура всех узлов установки равна температуре окружающей среды где Согласно (8.14) скорость убывания температуры пропорциональна разности температур установки и окружающей среды. Из (8.14) находим Выполняя интегрирование, получим где А − константа интегрирования, которая должна быть определена из начального условия Из (8.16) и (8.17) находим что соответствует экспоненциальному участку кривой d-e. Если бы потери отсутствовали, то процесс нагревания происходил бы по кривой a-b-cдо температуры Величина постоянной Чтобы найти постоянную калориметра, необходимо провести дополнительный эксперимент с жидкостью, теплоемкость которой хорошо известна, например с водой. Тогда из уравнения теплового баланса (8.12) можно найти постоянную калориметра где Методика эксперимента 1. В калориметр заливается вода при комнатной температуре 2. Одновременно включается нагреватель, мешалка и секундомер, регистрируется ток через нагреватель, через некоторое время (порядка минуты) фиксируется значение температуры. Данные заносятся в таблицу. 3. Когда вода нагреется на 10 градусов, нагреватель выключается. Вследствие инерции нагревателя после выключения тока температура некоторое время возрастает, затем начинает спадать, что также фиксируется, а данные записываются в таблицу. 4. После полного охлаждения воды она выливается из калориметра, который заполняется исследуемой жидкостью и опыт повторяется. Данные заносятся в таблицу. Обработка результатов 1. По данным полученным в п.1. строится график зависимости температуры от времени нагревания для калориметра с водой. 2. По формуле (8.20) определяется величина 3. По формуле (8.19) вычисляется температура 4. По формуле (8.21) рассчитывается постоянная калориметра При этом величина где 5. По данным получившимся в п. 2 строится график зависимости температуры от времени нагревания для калориметра с исследуемой жидкостью. 6. По формуле (8.20) находится величина 7. По формуле (8.19) вычисляется температура 8. По формуле (8.13) и найденному ранее значению постоянной калориметра вычисляется теплоемкость исследуемой жидкости. При этом 9. По методике расчета погрешностей косвенных измерений осуществить расчет погрешности постоянной охлаждения 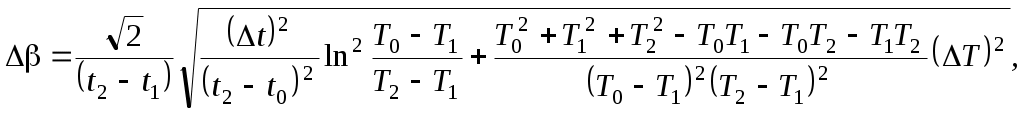 (8.23) (8.23)где 10. Найти погрешность определения температуры 11. Для воды определить погрешность где 12. Определить погрешность постоянной калориметра 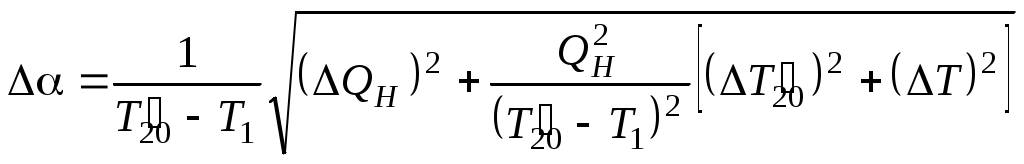 . (8.26) . (8.26)13. Найти погрешность определения постоянной охлаждения 14. Вычислить погрешность определения теплоемкости исследуемой жидкости по формуле 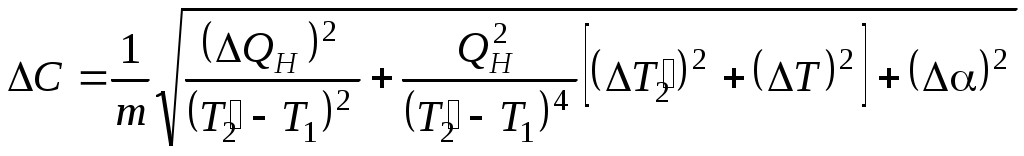 . (8.27) . (8.27)15.Представить окончательный результат в виде где Лабораторная работа 9 КОЛЕБАНИЯ СТРУНЫ Цель работы: изучение волновых явлений, условия существования стоячих волн, исследование упругих свойств струны. |
