Лабораторная работа 1 Основы измерений и обработки результатов

• Название: Лабораторная работа 1 Основы измерений и обработки результатов
• Дата: 22.04.2022
• Размер: 5.67 Mb.
• Имя файла: Mekhanika_mol_fiz_-_4.doc
• Тип: Лабораторная работа; #490736
• страница: 5 из 8

Коэффициент поверхностного натяжения
Цель работы: изучение основных свойств жидкости, знакомство с некоторыми экспериментальными методами измерения коэффициента поверхностного натяжения жидкости.

Основные теоретические положения

По своим свойствам жидкости похожи и на газы и на твёрдые тела. Этот двойственный характер связан с особенностью движения молекул жидкости. В твердом теле молекулы составляют кристаллическую решетку и колеблются около своего положения равновесия (тепловое их движение). В жидкостях среднее расстояние между молекулами больше, чем у кристаллов, и поэтому молекулы жидкости могут отходить от своих правильных положений. Молекулы жидкости совершают колебания около временных положений равновесия.

П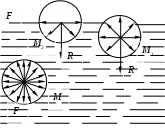
Рис. 6.1. Молекулы внутри жидкости и вблизи поверхности
обыв в таком положении некоторое время, молекула «перескакивает» в другое место и снова какое-то время живет в этом месте (совершая колебания) «оседлой жизнью». В «оседлом» состоянии молекулу удерживают упругие силы. Эти упругие силы обусловлены действием соседних молекул расположенных на близком расстоянии. Молекулярные силы очень быстро убывают с увеличением расстояния. Если по отношению к какой - то молекуле М (рис. 6.1), находящейся внутри жидкости, соседние молекулы расположены симметрично, то равнодействующая Rвсех сил, приложенных к молекуле М, равна нулю R= 0. Однако вследствие теплового движения равновесие нарушается, и молекула приходит в движение под влиянием равнодействующей силы R ≠ 0 . Силы притяжения между молекулами жидкости быстро убывают с увеличением расстояния. Они практически обращаются в нуль уже на расстоянии порядка 10^9 м. Поэтому результат воздействия на каждую молекулу определяется только ближайшими ее соседями. Он существенно зависит от того, где находится рассматриваемая молекула. Если последняя расположена внутри жидкости (на расстоянии, большем чем 10^9 м от границы жидкости), то силы взаимодействия со всеми окружающими ее молекулами в среднем уравновешиваются. В отличие от этого, среднее значение силы, действующей на молекулу поверхностного слоя жидкости толщиной порядка 10^9 м, не равно нулю; это обусловливается тем, что молекула, расположенная на поверхности, частично граничит с молекулами той же жидкости, а частично − с молекулами другой среды, например воздуха и пара или стенки. Вследствие разных плотностей и природы молекул сила, действующая на выделенную молекулу жидкости со стороны другой среды, отличается от силы ее взаимодействия с молекулами жидкости. В итоге результирующая сила, действующая на каждую молекулу поверхностного слоя, направлена либо внутрь жидкости, либо в сторону граничащей с ней среды. Поэтому при перемещении молекул из поверхностного слоя в глубь жидкости или наоборот из глубины жидкости на поверхность совершается работа. Эта работа тем больше, чем больше различие между силами взаимодействия молекул поверхностного слоя с молекулами жидкости и молекулами граничащей среды.

Молекулы жидкости, расположенные на поверхности, находятся в особом состоянии, например молекулы М₁ и М₂. Действие на эти молекулы со стороны молекул жидкости больше, чем со стороны молекул пара или воздуха, и поэтому равнодействующая всех действующих на молекулу М₁ и М₂ молекулярных сил направлена внутрь жидкости нормально к ее поверхности. Отсюда следует, что на все молекулы, расположенные в тонком поверхностном слое, действуют силы, стремящиеся втянуть их внутрь жидкости. Благодаря этому поверхностный слой давит с большой силой на жидкость, создавая в ней так называемое внутреннее или молекулярное давление. Это давление очень велико (для воды, например, около 11∙10⁸ н/м²).

Молекулы поверхностного слоя жидкости обладают избытком энергии сравнительно с молекулами, находящимися внутри жидкости. Эта избыточная энергия называется свободной поверхностной энергией или поверхностной энергией. Указанными свойствами поверхностного слоя обусловлено особое его состояние, которое подобно состоянию натянутой упругой пленки, стремящейся сократить свою поверхность до малых размеров.

Это стремление жидкости сократить свою свободную поверхность называется поверхностным натяжением.

Силы поверхностного натяжения F направлены по касательной к поверхности жидкости и действуют нормально к любой линии, проведенной на этой поверхности.

Для количественной характеристики силы поверхностного натяжения жидкости вводят коэффициент поверхностного натяжения α,который численно равен силе F, действующей на единицу длины произвольной линии L, мысленно проведенной на поверхности жидкости:

. (6.1)

В этом случае коэффициент поверхностного натяжения измеряется в ньютонах на метр (н/м).

Из рассмотрения свойств поверхностного слоя можно показать, что коэффициент поверхностного натяжения численно равен свободной поверхности энергии W, рассчитанной на квадратный метр поверхности жидкости S: .

Благодаря поверхностному натяжению любой объём жидкости стремится уменьшить площадь поверхности, уменьшая таким образом и потенциальную энергию. Крошечные капли воды имеют в воздухе почти сферическую форму, поскольку для сферы характерно меньшее отношение площади поверхности к объёму, чем для любой другой геометрической формы.

Коэффициент поверхностного натяжения различен для разных жидкостей. Он зависит от рода жидкости, температуры (уменьшается с повышением температуры) и от степени чистоты поверхности (изменяется от малейшего загрязнения).

С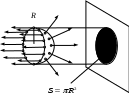
Рис. 6.2. Силы на полусфере мыльного пузыря
уществование поверхностного натяжения приводит к тому, что свободная поверхность жидкости ведёт себя так, как будто она сделана из упругой оболочки. Однако существует большое отличие между эластичностью этой оболочки, определяемой поверхностным натяжением, и эластичностью вещества типа резины. В случае плоской поверхности жидкости сила натяжения не зависит от того, насколько поверхность растянута. Для того чтобы увеличить площадь поверхности, вытягивая в поверхностный слой всё новые и новые молекулы, необходимо прикладывать постоянную силу. С другой стороны, чтобы растянуть резину, приходится прикладывать силу, пропорциональную растяжению.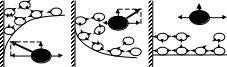

До сих пор мы рассуждали о поверхности между жидкостью и газом. У края сосуда жидкость находится в контакте и с
а б в
твёрдым телом, и с г
Рис. 6.3. Три различных случая контакта жидкости с твёрдым телом ( - результирующая сила, действующая на молекулу)
азом. На рис. 6.3 показ 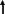аны три различных случая.

В первом случае (рис. 6.3 а) взаимодействие молекул жидкости с твердым телом достаточно сильно, чтобы изо­гнуть жидкость кверху на границе с твердым телом. В этом случае обычно говорят, что жид­кость смачивает поверхность твердого тела.

Такая ситуация характерна для воды, соприка­сающейся со стеклом. Во втором случае (рис.6.3 б) результирующая сила, действующая на жидкость на границе с твердым телом, на­правлена внутрь жидкости. Это не смачиваю­щаяся жидкость. Такая ситуация характерна для ртути в стеклянном сосуде. В третьем слу­чае (рис. 6.3 в) поверхность жидкости пер­пендикулярна стенке. Так ведет себя вода в со­судах из серебра и некоторых видов пластмасс.

Изогнутая поверхность жидкости в сосу­де называется мениском. При взаимодействии со стенкой сосуда силы поверхностного натяжения стремятся ли­бо поднять уровень жидкости, либо опустить его. Это называется капиллярным эффектом.

Капиллярныеявления.
В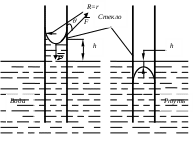
Рис. 6.4. Силы в капилляре
узких стеклянных трубках, капиллярах, опущенных в жидкость, хорошо заметно поднятие или опускание жидкости. Поверхностная пленка жидкости в трубке под действием молекулярных сил жидкости и стекла принимает вогнутую форму (вогнутый мениск). На такой искривленной поверхности силы поверхностного натяжения вызывают добавочное давление ∆p, обусловленное кривизной поверхности, направленное всегда в сторону вогнутой поверхности.

Название связано с тем, что высота подъема жидкости велика в достаточно уз­ких трубках, называемых капиллярами.

У верхнего края, где жидкость касается стекла, форма её поверхности очень похожа на полусферу мыльного пузыря, которую мы рассматривали(рис. 6.4). Си­ла поверхностного натяжения направлена вдоль поверхности жидкости. Вер­тикальная составляющая этой силы равна
.
Она уравновешивается силой тяжести столба жидкости с плотностью : . Таким образом, имеем . Следовательно
. (6.2)

Если жидкость в капилляре не смачивающая, уровень её в капилляре оказывается ниже уровня в жидкости в широком сосуде. Это в точности такой же эффект, и описывается он той же формулой (6.2).
Описание экспериментальной установки и последовательность

проведения измерений
И 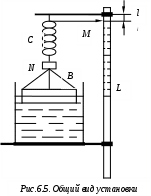сследуемая жидкость находится в сосуде А. Кольцо В, изготовленное из материала, хорошо смачиваемого этой жидкостью, подве­шено на пружине С.

1. Определить коэффициент упругости пружины k, для чего на чашечку 2 положить груз m и отметить растяжение пружины x. Вычислить k по формуле

(6.3)

Измерения провести 3−4 раза с разными грузами и затем определить среднее значение .

2. Измерить длину пружины , затем кольцо опустить в сосуд с водой. Сосуд опускать вниз до отрыва кольца от воды. Измерить длину пружины в момент отрыва кольца от воды. Эксперимент провести 5−6 раз.

3. 
   Измерить штангенциркулем наружный и внутренний диаметры кольца D и d, а затем определить сумму наружной и внутренней длин окружностей кольца L
   

_, (6.4)
а затем найти коэффициент поверхностного натяжения
. (6.5)
Обработка результатов эксперимента

1. 
   Величина полной погрешности определения определяется по формуле
   

, (6.6)

где

, (6.7)
, (6.8)

где − приборная погрешность линейки.

Погрешности и определяются по методике расчета погрешностей прямых измерений.

2. Результат представить в виде _.
Определение коэффициента поверхностного натяжения методом поднятия жидкости в капилляре
Капилляр вставляется в широкий сосуд с исследуемой жидкостью. С помощью масштабной линейки определяется высота подъёма жидкости h. Этот опыт проводится не менее 5 раз.

Если известен радиус rкапилляра, то сила поверхностного натяжения:

(6.9)
Сила тяжести столба жидкости равна , а так как F=P, то получаем , то есть

. (6.10)
Обработка результатов и расчёт погрешностей

1. 
   Погрешность величины hопределить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность и коэффициент Стьюдента.
   
2. 
   Погрешность косвенных измерений величины aрассчитать по формуле
   

. (6.11)

3. 
   Результат записать в виде: .
   

Представляет интерес сравнение величин коэффициентов поверхностного натяжения одной и той же жидкости, полученных различными методами, и погрешностей их определения.


Лабораторная работа 7

ИЗМЕРЕНИЕ ГАЗОВОЙ ПОСТОЯННОЙ
Цель работы: изучение газовых законов, экспериментальная проверка уравнения состояния идеального газа, ознакомление с работой газового термометра.

Основные теоретические положения
В молекулярно-кинетической теории объектом исследования является идеализированная модель реального газа − идеальный газ. Идеальным газом на­зывается газ, между молекулами которого отсутствуют силы взаимодействия. При этом принимается, что при соударениях между собой и со стенками сосуда молекулы такого газа ведут себя как абсолютно упругие шарики конечных, но весьма малых размеров. Эти соударения молекул происходят по законам абсо­лютно упругого удара.

Величинами, определяющими состояние газа, являются: давление р, под которым он находится, его температура Т , объем V, занимаемый определенной массой газа М. Величины p, V, T, Mназываются параметрами состояния. Давлением Р называется физическая величина, равная пределу отношения численного значения нормальной силы ,действующей на единицу поверхности , к величине этой поверхности:



Единицей давления в системе СИ является паскаль ([P]=[F]/[S]= H/ =Па)

Температурой называется физическая величина, характеризующая сте­пень нагретости тела.

Параметры состояния связаны между собой различными газовыми законами.

Если газ находится при постоянной температуре T=const, то объем газа и давление связаны законом Бойля-Мариотта pV=const.

При постоянном объеме − это закон Шарля, в котором − термический коэффициент давления, и − давление газа при начальной и конечной температуре.

П
Рис. 7.1. К выводу уравнения состояния идеального газа
ри постоянном давлении объем газа пропорционален температуре и определяется законом Гей–Люссака: , где термический коэффициент объемного расширения, − объемы газа при начальной и конечной температуре.
Теперь возвращаемся к уравнению состояния идеального газа, то есть найдём связь между P, VиT. Рассмотрим определённую массу газа m, которая заполняет объём , имеет давление и находится при температуре . Пусть в другом состоянии та же масса газа характеризуется объёмом, давлением и температурой: , , . Установим на основании законов Бойля-Мариотта, Гей-Люссака и Шарля связь между , , и , , . Для этого сначала газ из состояния , и при постоянном давлении нагреем до температуры . По закону Гей-Люссака . Так как , то . Из этого состояния в окончательное состояние, характеризующееся параметрами , , , его можно перевести изотермическим изменением объёма, для которого по закону Бойля-Мариотта имеем: . Подставляя , получим , то есть , откуда следует, что при изменении состояния данной массы газа величина PV/T остаётся постоянной, то есть PV/T=B.

Если это соотношение относить к одному молю, то постоянная Вбудет иметь одно и то же значение для всех газов. Эта общая для всех газов постоян­ная обозначается Rи носит название универсальной газовой постоянной. Вводя в предыдущую формулу вместо объема Vмолярный объем V_о, то есть объем одного моля газа, получим

. (7.1)

Эта формула представляет собой уравнение состояния идеального газа и носит название уравнения Менделеева-Клапейрона.

Уравнение Менделеева-Клапейрона, справедливое для одного моля газа, можно обобщить и на любую массу. Если — молярная масса и при некотором данном давлении и температуре 1 моль газа занимает объем ,то при том же давлении и температуре т граммов газа займут объем . Тогда и, подставляя в уравнение Менделеева-Клапейрона (7.1), получим

. (7.2)

В работе предлагается на опыте убедиться в справедливости формулы (7.2), а также определить универсальную газовую постоянную.
Описание лабораторной установки и последовательность проведения измерений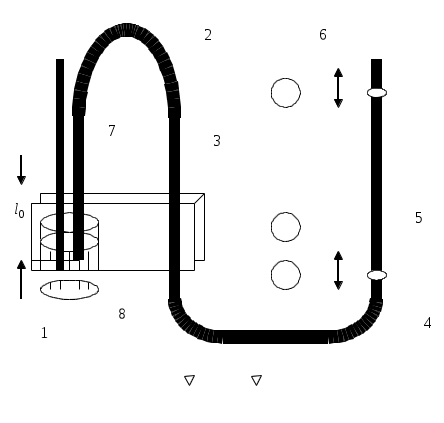


Рис. 7.2.Экспериментальная установка
Прибор состоит из стеклянной трубки 1, запаянной с одного конца и газового термометра Жоли, частями которого являются: соединительная резиновая трубка 2, смотровая стеклянная трубка 3, резиновый шланг 4, стеклянная трубка 5; трубка 7, соединенная с резервуаром 8. Все стеклянные трубки имеют одинаковое сечение. Прибор крепится на штативе 6 и заполняется водой так, чтобы ее уровень располагался посредине трубок 3 и 5. Уровень воды в трубке 3 отмечается резиновым колечком.

Задание 1. Проверка уравнения состояния идеального газа (7.2).

При равенстве уровней воды в трубках 3 и 5 измеряется длина воздушного столба от уровня воды в трубке 1. Объём воздуха пропорционален длине столба плюс объём колбы , то есть . Давление воздуха равно атмосферному . Температура воздуха равна температуре воздуха в лаборатории и определяется по термометру. Параметры указанного состояния , , , а величина .

Включается нагреватель, и температура воды в стакане увеличивается до . При этом уровень воды в трубке 5 поднимается, то есть газ в колбе 1 расши­ряется и его часть выходит из объёма колбы. Если перемещать трубку 5 вверх − вниз на величину , то можно добиться равенства уровня воды в труб­ках 3 и 5. Тогда давление воздуха в колбе 1 будет равно атмосферному давле­нию , а длина воздушного столба или объём , где , − поперечное сечение трубки. Получаются вторые данные , , . Далее во­да в стакане нагревается до температуры и проделывается то же, что и с холодной водой. Получается третий набор данных: , , . Все полученные данные измерений заносятся в таблицу.

Величина (j=1,2) рассчитывается следующим образом. В каждом эксперименте при нагревании колбы до температуры объём газа в ней увеличивается на , и при этом высота жидкости в манометре изменяется на . Поэтому на основании уравнения (7.2)
,

откуда изменение объёма равно , то есть , а .

Обработка результатов и расчёт погрешностей

1. 
   Приборную погрешность величины 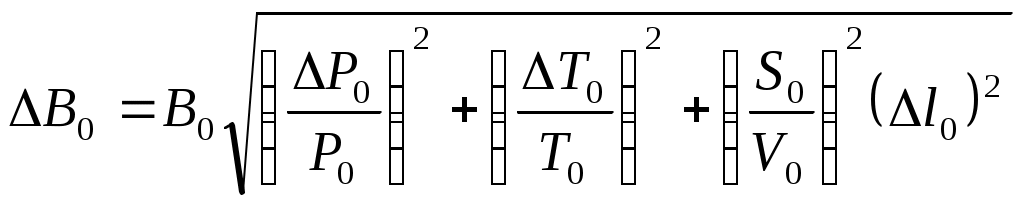определить по формуле
   

. (7.3)

2. 
   Результат представить в виде .
   
3. 
   Погрешность величины 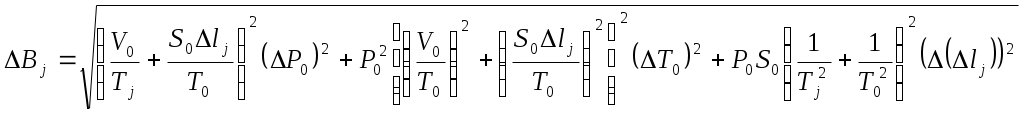(j=1,2) рассчитать по формуле
   

. (7.4)

4. 
   Результат представить в виде: , .
   
5. 
   Сравнить величины , , и сделать вывод о формуле (7.2).
   

Задание 2. Определение универсальной газовой постоянной

Обработка результатов и расчёт погрешностей.

1. 
   Величину газовой постоянной для двух случаев j 1,2 рассчитать по формуле
   

, (7.5)

считая, что величины и являются приборными константами.

2. 
   Погрешность вычислить с учётом зависимости (7.4) по формуле
   

. (7.6)

3. 
   Результат представить в виде , j=1,2.
   
4. 
   Сравнить величины и с табличным значением R.
   

Задание 3. Определение газовой постоянной методом измерения объема и давления паров жидкости.

Если в сосуд известного объема ввести определенную массу легко испаряющейся жидкости, а после того, как она полностью испарится, измерить, насколько увеличится давление внутри сосуда, то, зная молекулярную массу жидкости и температуру, можно вычислить R по формуле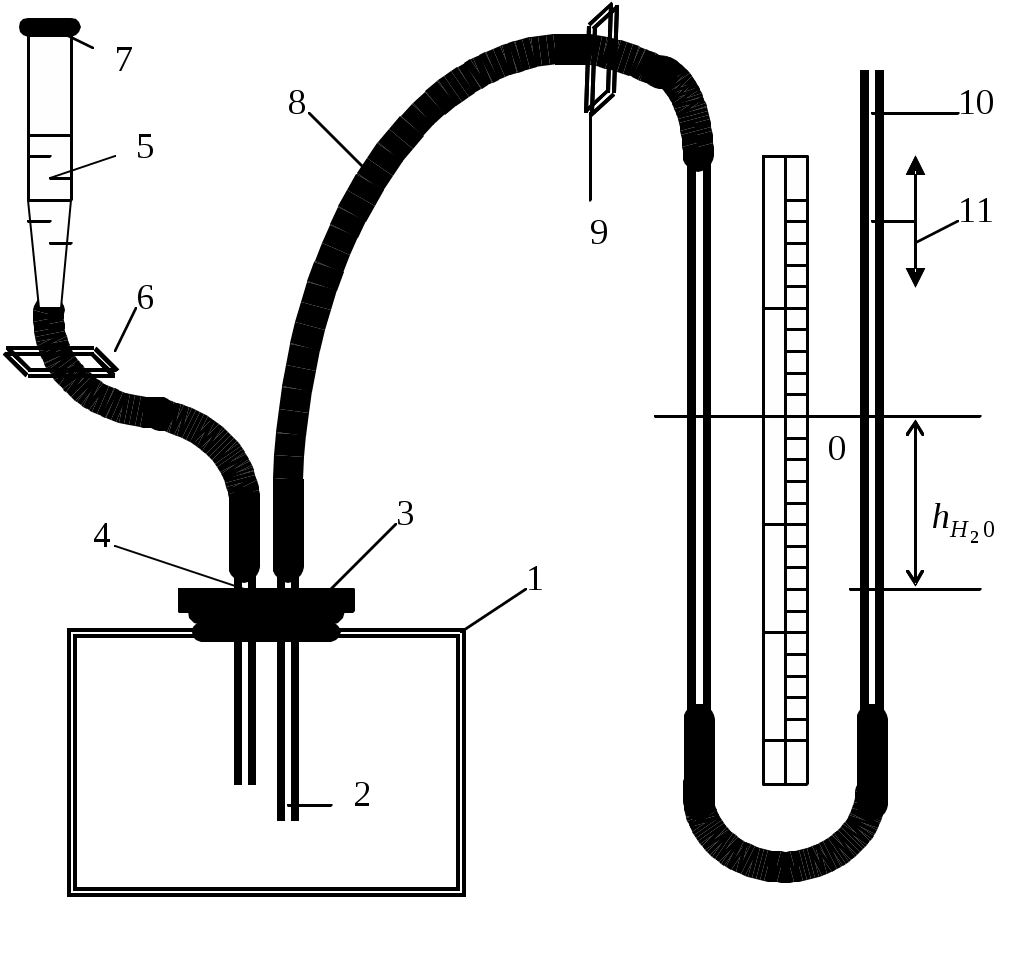
(7.7)



У
Рис. 7.3 Схема экспериментальной

установки
становка (рис. 7.3) состоит из стеклянного сосуда 1, закрытого резиновой пробкой 3 с двумя отверстиями: в одно вставлена стеклянная трубка 2, в другое − 4 микробюретка с ацетоном. На верхний конец микробюретки 5 надета резиновая трубка с винтовым зажимом 6. Конец трубки закрыт пробкой 7. Сосуд 1 соединен с левым коленом водяного манометра 10 с помощью резиновой трубки 8 и стеклянного тройника с краном 9. Правое колено манометра подвижно. Его положение фиксируется зажимом 11.

В сосуд вводится ацетон из микробюретки: _ац= 0,058 кг/моль, 790 кг/м³,

, (7.8)

где V_ац – объем ацетона, введенного в сосуд.

Так как парциальное давление паров ацетона измеряется водяным манометром по разности уровней воды в его коленах, то

(7.9)

где разность уровней воды в коленах манометра.

Учитывая (7.8) и (7.9), можно записать

(7.10)

Первый сомножитель в (7.8) является величиной постоянной, второй − постоянен для конкретных условий проведения опыта при постоянной температуре и объеме сосуда. Таким образом определение R сводится к измерению объема жидкого ацетона, введенного в сосуд, и разности уровней воды в коленах манометра, обусловленной давлением паров ацетона. Точный объем сосуда с учетом объема резинового шланга, соединяющего сосуд с манометром и объема трубки манометра до уровня нулевой отметки написан на стенке сосуда. Работа выполняется в такой последовательности:

1. Измеряется объем ацетона микробюретке.

2. Открывается кран у тройника 9 и перемещением правого колена манометра уровень воды устанавливается на нулевую отметку шкалы. После этого закрывается кран 9.

3. Весь ацетон из микробюретки выливается в сосуд, в результате чего изменяются показания манометра. После того, как весь ацетон испарится, показания манометра перестанут изменяться.

4. Передвижением правого колена манометра устанавливается уровень воды в левом колене на нулевую отметку. Это необходимо сделать для сохранения объема воздуха в сосуде и трубках таким же, как в начале опыта. Тогда манометр покажет только парциальное давление паров ацетона, так как температура не изменилась.

5. По шкале манометра отсчитывается разность уровней воды и в его коленах и данные записываются в таблицу.
Обработка результатов

1. Газовая постоянная вычисляется по формуле (7.11).

2. Так как измеряется только одна переменная 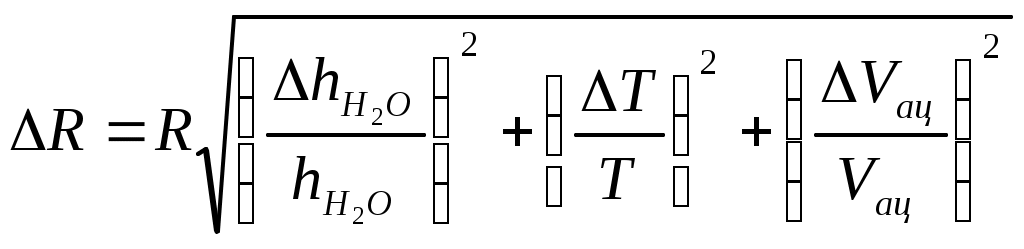один раз, то предельная погрешность косвенных измерений величины R определяется по формуле

, (7.11)
где , и − систематические погрешности определения разности уровней в манометре после испарения ацетона, температуры и объёма ацетона.

3. Сравниваются величины газовой постоянной, полученные разными методами, и погрешности этих методов.

4. Если измерения проводятся несколько раз, то процедура расчёта погрешностей несколько отличается. В этом случае при измерениях изменяются две величины: 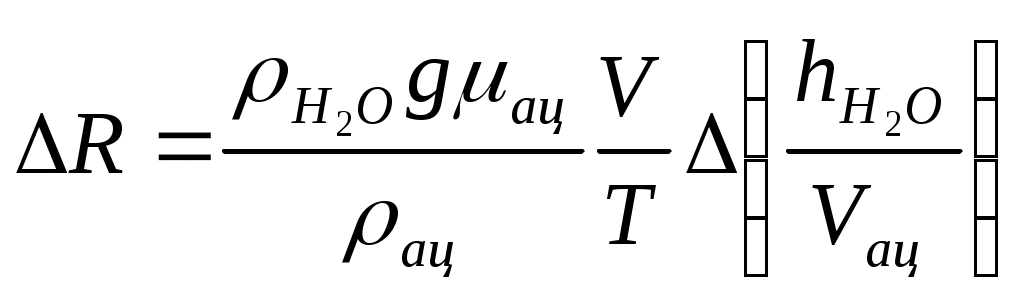, . Поэтому

, (7.12)
где погрешность величины / необходимо определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность и коэффициент Стьюдента.
Лабораторная работа 8