ЛР1. Лабораторная работа 1 по дисциплине Математические основы теории систем

• Название: Лабораторная работа 1 по дисциплине Математические основы теории систем
• Дата: 24.09.2022
• Размер: 84.13 Kb.
• Имя файла: ЛР1.docx
• Тип: Лабораторная работа; #693874

Министерство науки и высшего образования

Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ

УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра компьютерных систем в управлении и проектировании (КСУП)
Лабораторная работа №1

по дисциплине «Математические основы теории систем»

выполнена по методике Карпов А.Г. «Математические основы теории систем, 2002 г.»

Вариант 3


Выполнил студент

Группа!!!!!!!!!!!!!!

!!!!!!!!!!!!!!!!

25 September 2022 г.

Руководитель работы

_________________/Должность/

_________________Ф.И.О.

_________________/Подпись/

_________________/Дата/

ТОМСК 2022 г
ЗАДАНИЕ
1. Разложить заданный автомат А на автономные: 

а) по входным буквам ; 

б) по выходным буквам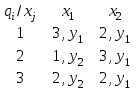 



а) по входным буквам :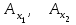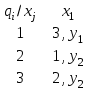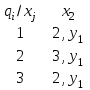





б) по выходным буквам:

по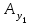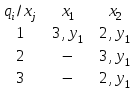



по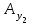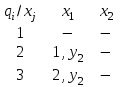



2. По автомату Мили построить эквивалентный ему автомат Мура, используя теорему 4.2.2 [1]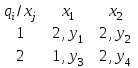



Решение:

Для исходного автомата S имеем:

Q={q₁,q₂};

X={x₁, x₂};

Y={y₁,y₂,y₃,y₄};

функции  и  опишем матрично: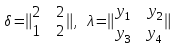

по теореме 4.2.2 пособия для эквивалентного автомата Мура S_м имеем:

X_м =X ;

Y_м = Y ;

Q_м={q₁₀,q₂₀, q₁₁,q₁₂,q₂₁,q₂₂}, где состояния q₁₀, q₂₀ соответствуют состояниям q₁, q₂, а q₁₁,q₁₂,q₂₁,q₂₂ соответствуют парам (q₁, x₁), (q₁, x₂), (q₂, x₁), (q₂, x₂) автомата S.

Функция _м определяется так:

по формуле _м(q_i0, x_k)=q_ik имеем

_м(q₁₀, x₁)=q₁₁;

_м(q₁₀, x₂)=q₁₂;

_м(q₂₀, x₁)=q₂₁;

_м(q₂₀, x₂)=q₂₂;
По формуле _м(q_ij, x_k)=q_lk , где l — номер состояния, определяемого переходной функцией исходного автомата S — _м(q_i, x_j)=q_l, имеем:

_м(q₁₁, x₁)=q₂₁;

_м(q₁₁, x₂)=q₂₂;

_м(q₁₂, x₁)=q₂₁;

_м(q₁₂, x₂)=q₂₂;

_м(q₂₁, x₁)=q₁₁;

_м(q₂₁, x₂)=q₁₂;

_м(q₂₂, x₁)=q₂₁;

_м(q₂₂, x₂)=q₂₂;
Функция отметок в автомате Мура однозначно определена текущим состоянием, имеем:

(q₁₀), (q₂₀) не определены

(q₁₁)=y₁;

(q₁₂)=y₂ ;

(q₂₁)=y₃;

(q₂₂)=y₄;

В результате получаем автомат Мура, заданный таблицей:

qij/xk	x1	x2	
q10	q11	q12	-
q20	q21	q22	-
q11	q21	q22	y1
q12	q21	q22	y2
q21	q11	q12	y3
q22	q21	q22	y4

3. По автомату Мура построить эквивалентный ему автомат Мили.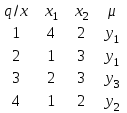 


Таблицы переходов автомата Мили и эквивалентного ему автомата Мура совпадают. Таблица выходов автомата Мили составляется так, что в каждую клетку таблицы записывается выходной сигнал, которым отмечено состояние, расположенное в данной клетке.

	x1	x2
1	4, y2	2, y1
2	1, y1	3, y3
3	2, y1	3, y3
4	1, y1	2, y1

4. Найти автоматные отображения слов для заданного автомата, предполагая, что: 

а) функция выхода обычная (автомат 1-го рода); 

б) функция выхода сдвинутая (автомат 2-го рода).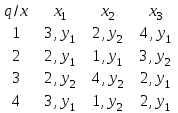 

x = x₂x₁x₂x₁x₂x₃x₃

В качестве начального состояния примем q₁.

Для автомата первого рода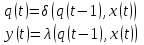



Получаем ленту автомата:

Такт	0	1	2	3	4	5	6	7
Х	-	х2	х1	х2	х1	х2	х3	х3
Q	1	2	2	1	3	4	2	3
Y	-	y2	y1	y1	y1	y2	y1	y2

Для автомата второго рода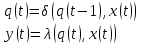



Получаем ленту автомата:

Для автомата второго рода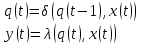



Получаем ленту автомата:

Такт	0	1	2	3	4	5	6	7
Х	-	х2	х1	х2	х1	х2	х3	х3
Q	1	2	2	1	3	4	2	3
Y	-	y1	y1	y2	y2	y2	y2	y1

5. Минимизировать автомат, используя алгоритм Мили. 


Решение:

Шаг 1. Найдём все классы разбиения, для которых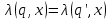

Разбиение Q = {C_11,C₁₂, C₁₃}, где

C₁₁={1, 5, 7, 8}; C₁₂={2, 3}; C₁₃ = {4, 6, 9},
Шаг 2. Найдём разбиения среди выделенных классов, для каждого x которых 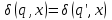принадлежат одному подклассу C_ij.
Для класса C₁₁, происходит разбиение на:

C₂₁={1, 7}; C₂₂={5};C₂₃={8};
Для класса C₁₂, разбиение не происходит:
Для класса C_13, происходит разбиение на:

C₂₄={4}; C₂₅={6}; C₂₆={9}.
Шаг 3. Найдём разбиения среди выделенных классов
Класс C₂₁ разбивается на:

C₃₁={1}; C₃₂={7};
Класс C₁₂ разбивается на:

C₃₃={2}; C₃₄={3};

Остальные классы не разбиваются.
Шаг 4. Даёт аналогичное разбиение как на предыдущем шаге — алгоритм закончен.

В результате мы получили такое количество классов, как и общее число состояний в исходном автомате. Это означает, что автомат уже минимизирован.

6. Написать формулу в алгебре Клини, задающую событие в алфавите {a, b, c}. 

Все слова, содержащие b четное число раз.
Рассмотрим два варианта:

Слово начинается с буквы b. Между буквами b может быть любое количество символов. Имеем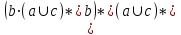

Начинаться слово может с буквы a или c, т.е.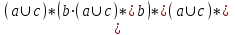

Таким образом: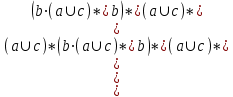



7. Синтезировать автомат (на абстрактном уровне), представляющий регулярное событие.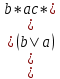 


Построение источника H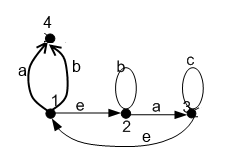


Детерминизация источника H:

	a	b	c
{1,2 }	{1,2,3,4}	{2,4}	Ǿ
{1,2,3,4}	{1,2,3,4}	{2,4}	{1,2,3}
{2,4}	{1,2,3}	{2}	Ǿ
{1,2,3}	{1,2,3,4}	{2,4}	{1,2,3}
{2}	{1,2,3}	{2}	Ǿ
Ǿ	Ǿ	Ǿ	Ǿ

После переобозначения подмножеств таблица переходов автомата приобретает следующий вид:

	a	b	c
1	2	3	6
2	2	3	4
3	4	5	6
4	2	3	4
5	4	5	6
6	6	6	6

8. Провести анализ автомата (написать выражение регулярного события, представляемого автоматом). Начальное состояние - 1, заключительное - 4.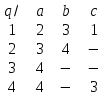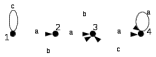 



Выражение регулярного события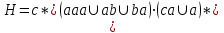