Лабораторная работа 1 По дисциплине Основы теории управления Динамические характеристики типовых звеньев Студенты Белов А., Юдин Ф
 Скачать 2.42 Mb. Скачать 2.42 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ  Лабораторная работа №1 По дисциплине «Основы теории управления» Динамические характеристики типовых звеньев Студенты: Белов А., Юдин Ф. Дата сдачи: Преподаватель: Воевода А. А., д.т.н., профессор кафедры автоматики Оглавление1.Цель работы 3 2.Теоретические сведения 3 2.1 Апериодическое звено 3 2.2 Дифференцирующие звенья 8 2.3 Колебательное звено 9 2.4 Усилительное звено 11 2.5 Интегрирующее звено 11 2.6 Реально дифференцирующее звено 13 3.Ход работы 15 3.1 Апериодическое звено 15 3.2 Дифференцирующее звено 20 3.3 Колебательное звено 22 3.4 Усилительное звено 25 3.5 Интегрирующее звено 28 3.6 Реально дифференцирующее звено 31 Вывод 37 Цель работыИсследовать динамические характеристики типовых звеньев систем автоматического управления (САУ), а также познакомиться с представлением типовых звеньев структурными схемами. При выполнении лабораторных работ используется пакет программ Matlab/Simulink Теоретические сведения2.1 Апериодическое звеноОдно из самых часто встречающихся звеньев – апериодическое, которое описывается дифференциальным уравнением: 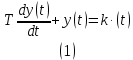 и имеет передаточную функцию 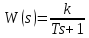 . Здесь . Здесь 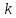 безразмерный коэффициент, а безразмерный коэффициент, а 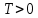 – постоянная, которая называется постоянной времени звена. Постоянная времени – размерная величина, она измеряется в секундах и характеризует инерционность объекта, то есть скорость его реакции на изменение входного сигнала. Переходная (2) и весовая (3) функции апериодического звена: – постоянная, которая называется постоянной времени звена. Постоянная времени – размерная величина, она измеряется в секундах и характеризует инерционность объекта, то есть скорость его реакции на изменение входного сигнала. Переходная (2) и весовая (3) функции апериодического звена: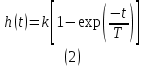  Они показаны на рисунке: 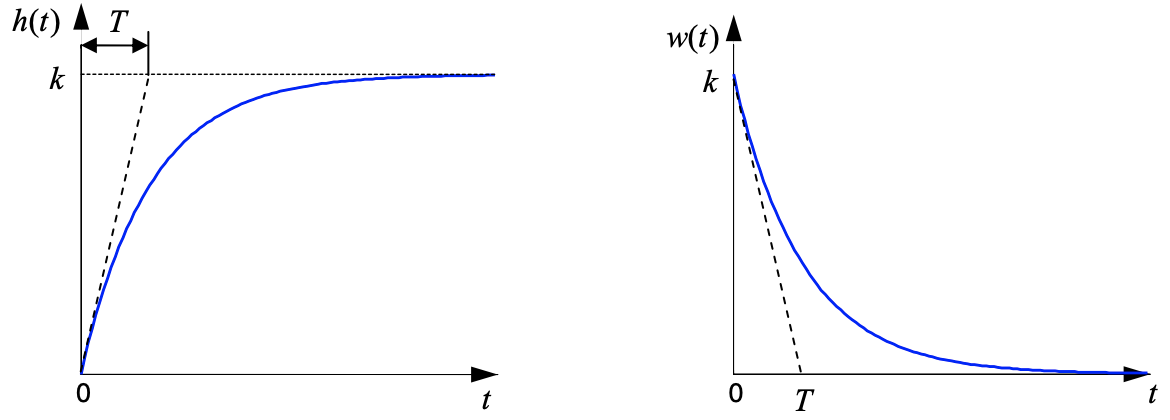 Рисунок 1 — Переходная (2) и весовая (3) функции апериодического звена Обратите внимание, что предельное значение переходной характеристики равно 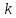 , а касательная к ней в точке , а касательная к ней в точке 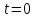 пересекается с линией установившегося значения при пересекается с линией установившегося значения при 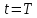 . Переходная и импульсная характеристики выходят на установившееся значение (с ошибкой не более 5%) . Переходная и импульсная характеристики выходят на установившееся значение (с ошибкой не более 5%)примерно за время 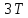 . Эти факты позволяют определять постоянную времени экспериментально, по переходной характеристике звена. . Эти факты позволяют определять постоянную времени экспериментально, по переходной характеристике звена.Частотная характеристика определяется выражением: 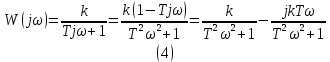 Для каждой частоты 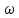 значение значение 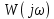 – это точка на комплексной плоскости. При изменении – это точка на комплексной плоскости. При изменении 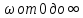 получается кривая, которая называется годографом Найквиста (диаграммой Найквиста). В данном случае можно показать, что частотная характеристика – это полуокружность с центром в точке получается кривая, которая называется годографом Найквиста (диаграммой Найквиста). В данном случае можно показать, что частотная характеристика – это полуокружность с центром в точке 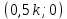 радиуса радиуса 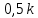 . Годограф начинается (на нулевой частоте в точке . Годограф начинается (на нулевой частоте в точке 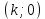 и заканчивается в начале координат и заканчивается в начале координат 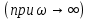 . . 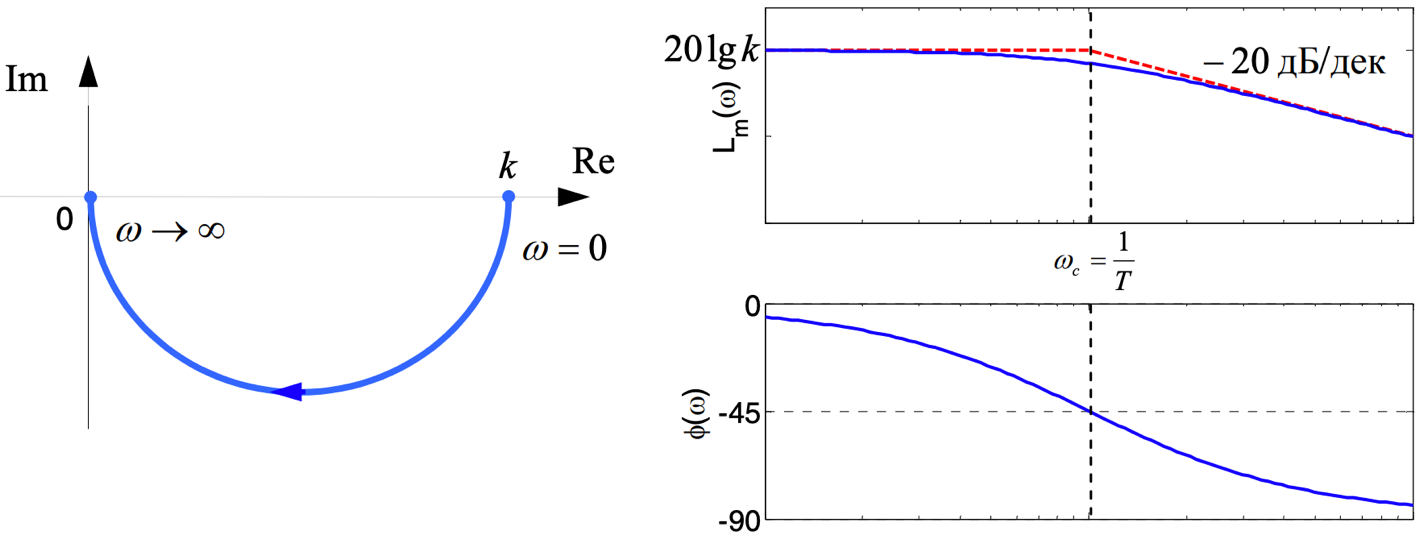 Рисунок 2 – Диаграмма Найквиста; диаграмма Боде Асимптотическая ЛАЧХ этого звена образована двумя прямыми, которые пересекаются на сопрягающей частоте 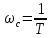 . На низких частотах она имеет нулевой наклон (так как звено позиционное), причем в этой области . На низких частотах она имеет нулевой наклон (так как звено позиционное), причем в этой области 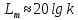 . . На высоких частотах наклон ЛАЧХ равен − 20 дБ/дек, так как степень знаменателя передаточной функции на единицу больше степени ее числителя. Фазовая характеристика меняется от 0 до −90°, причем на сопрягающей частоте 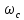 она равна −45°. она равна −45°. Поскольку ЛАЧХ уменьшается на высоких частотах, апериодическое звено подавляет высокочастотные шумы, то есть обладает свойством фильтра низких частот. Для сравнения рассмотрим также неустойчивое апериодическое звено, которое задается уравнением 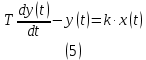 Как видим, все отличие от (4) – только в знаке в левой части уравнения (плюс сменился на минус). Однако при этом кардинально меняются переходная и импульсная характеристики: 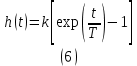   Рисунок 3 – График переходной характеристики Обычно предполагается, что постоянная времени  , тогда экспоненты в этих выражениях бесконечно возрастают с ростом t. Поэтому звено названо «неустойчивым»: в покое оно находится в неустойчивом равновесии, а при малейшем возмущении «идет вразнос». , тогда экспоненты в этих выражениях бесконечно возрастают с ростом t. Поэтому звено названо «неустойчивым»: в покое оно находится в неустойчивом равновесии, а при малейшем возмущении «идет вразнос».Интересно сравнить частотные характеристики устойчивого и неустойчивого апериодических звеньев с теми же коэффициентами усиления и постоянными времени.  Рисунок 4 – ЛАЧХ и АФЧХ Из этого графика видно, что ЛАЧХ неустойчивого звена точно совпадает с ЛАЧХ аналогичного устойчивого, но отрицательный фазовый сдвиг значительно больше. Устойчивое апериодическое звено относится к минимально–фазовым звеньям, то есть его фаза по модулю меньше, чем фаза любого звена с такой же амплитудной характеристикой. Соответственно, неустойчивое звено – неминимально–фазовое. К неминимально–фазовым звеньям относятся все звенья, передаточные функции которых имеют нули или полюса в правой полуплоскости, то есть, с положительной вещественной частью. Для минимально–фазовых звеньев все нули и полюса передаточной функции находятся в левой полуплоскости (имеют отрицательные вещественные части). Например, при положительных постоянных времени 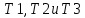 звено с передаточной функцией звено с передаточной функцией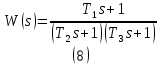 – минимально–фазовое, а звенья с передаточными функциями 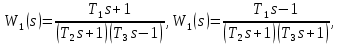 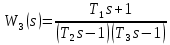 – неминимально–фазовые. 2.2 Дифференцирующие звеньяДифференцирующее звено дает на выходе производную входного сигнала. Уравнение идеального дифференцирующего звена 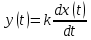 , его операторная запись , его операторная запись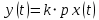 , а передаточная функция , а передаточная функция 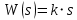 . .Известно, что производная единичного ступенчатого сигнала 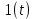 в точке в точке – это дельта-функция – это дельта-функция  . Поэтому переходная и весовая функции дифференцирующего звена . Поэтому переходная и весовая функции дифференцирующего звена Это физически нереализуемые функции, так как дельта-функцию и ее производную, имеющие бесконечные значения, невозможно получить на реальном устройстве. Поэтому идеальное дифференцирующее относится к физически нереализуемым звеньям. Логарифмическая амплитудная частотная характеристика дифференцирующего звена – прямая с наклоном 20 дБ/дек, пересекающая ось абсцисс  на частоте на частоте  . При . При  ЛАЧХ равна ЛАЧХ равна  . Дифференцирующее звено подавляет низкие частоты (производная от постоянного сигнала равна нулю) и бесконечно усиливает высокочастотные сигналы, что требует бесконечной̆ энергии и невозможно в физически реализуемых системах. . Дифференцирующее звено подавляет низкие частоты (производная от постоянного сигнала равна нулю) и бесконечно усиливает высокочастотные сигналы, что требует бесконечной̆ энергии и невозможно в физически реализуемых системах.  Рисунок 5 – Как-то надо подписать 2.3 Колебательное звеноКолебательное звено – это звено второго порядка с передаточной функцией вида  знаменатель которой имеет комплексно-сопряженные корни (то есть,  ). Как известно из теории дифференциальных уравнений, свободное движение такой системы содержит гармонические составляющие (синус, косинус), что дает колебания выхода при изменении входного сигнала. ). Как известно из теории дифференциальных уравнений, свободное движение такой системы содержит гармонические составляющие (синус, косинус), что дает колебания выхода при изменении входного сигнала.Несложно представить передаточную функцию колебательного звена в форме  где  – коэффициент, – коэффициент,  – постоянная времени (в секундах), – постоянная времени (в секундах),  – параметр затухания ( – параметр затухания ( ). Постоянная времени определяет инерционность объекта, чем она больше, тем медленнее изменяется выход при изменении входа. Чем больше ). Постоянная времени определяет инерционность объекта, чем она больше, тем медленнее изменяется выход при изменении входа. Чем больше  , тем быстрее затухают колебания. , тем быстрее затухают колебания.При  получается консервативное звено, которое дает незатухающие колебания на выходе. Если получается консервативное звено, которое дает незатухающие колебания на выходе. Если  , модель представляет апериодическое звено второго порядка, то есть последовательное соединение двух апериодических звеньев. , модель представляет апериодическое звено второго порядка, то есть последовательное соединение двух апериодических звеньев.Колебательное звено относится к позиционным звеньям, его статический коэффициент усиления равен  . .Переходная и импульсная характеристики отличаются выраженной колебательностью, особенно при малых значениях параметра затухания  . На следующих двух графиках синие линии соответствуют . На следующих двух графиках синие линии соответствуют  , а красные – , а красные –  . . Рисунок 6 – Переходная и импульсная характеристики колебательного звена. Асимптотическая ЛАЧХ этого звена образована двумя прямыми, которые пересекаются на сопрягающей частоте  . На низких частотах она имеет нулевой наклон (так как звено позиционное), причем в этой области . На низких частотах она имеет нулевой наклон (так как звено позиционное), причем в этой области  . .   Рисунок 7 – Диаграмма Боде. На высоких частотах наклон ЛАЧХ равен − 40 дБ/дек, так как степень знаменателя передаточной функции на два больше степени ее числителя. Фазовая характеристика меняется от 0 до −180°, причем на сопрягающей частоте c ω она равна − 90°. При значениях  ЛАЧХ имеет так называемый «горб» в районе сопрягающей частоты, причем его высота увеличивается с уменьшением ЛАЧХ имеет так называемый «горб» в районе сопрягающей частоты, причем его высота увеличивается с уменьшением  . Это означает, что при частоте входного сигнала, равной c . Это означает, что при частоте входного сигнала, равной c  , наблюдается резонанс, то есть частота возмущения совпадает с частотой собственных колебаний системы. , наблюдается резонанс, то есть частота возмущения совпадает с частотой собственных колебаний системы.В предельном случае при  (консервативное звено) ЛАЧХ терпит разрыв (обращается в бесконечность) на частоте c (консервативное звено) ЛАЧХ терпит разрыв (обращается в бесконечность) на частоте c  , при таком входе амплитуда колебаний неограниченно растет и на практике объект разрушается. , при таком входе амплитуда колебаний неограниченно растет и на практике объект разрушается.2.4 Усилительное звеноЗвенья, имеющие конечный ненулевой коэффициент усиления постоянного сигнала, то есть  , называются позиционными. Это значит, что числитель и знаменатель передаточной функции имеют ненулевые свободные члены (постоянные слагаемые). , называются позиционными. Это значит, что числитель и знаменатель передаточной функции имеют ненулевые свободные члены (постоянные слагаемые).Простейшее позиционное звено – идеальный (безынерционный) усилитель. Его передаточная функция  . Строго говоря, он не является динамическим звеном, поскольку изменение выхода происходит мгновенно, сразу вслед за изменением входа. При действии на вход единичного ступенчатого сигнала . Строго говоря, он не является динамическим звеном, поскольку изменение выхода происходит мгновенно, сразу вслед за изменением входа. При действии на вход единичного ступенчатого сигнала  (или дельта-функции (или дельта-функции  ) на выходе будет такой же сигнал, усиленный в ) на выходе будет такой же сигнал, усиленный в  раз, поэтому переходная и импульсная характеристики звена равны раз, поэтому переходная и импульсная характеристики звена равны Если на вход усилителя действует синусоидальный сигнал, на выходе он усиливается в  раз без изменения фазы, поэтому амплитудная и фазовая частотная характеристики не зависят от частоты входного сигнала: раз без изменения фазы, поэтому амплитудная и фазовая частотная характеристики не зависят от частоты входного сигнала: 2.5 Интегрирующее звеноПростейший пример интегрирующего звена – ванна, в которую набирается вода. Входной сигнал – это поток воды через кран, выход системы – уровень воды в ванне. При поступлении воды уровень растет, система «накапливает» (интегрирует) входной сигнал. Интегрирующее звено описывается уравнением  которому соответствует передаточная функция  . Решение уравнения дает . Решение уравнения дает . .Используя это решение для единичного скачка (  при при  ) при нулевых начальных условиях ( ) при нулевых начальных условиях ( ), получаем линейно возрастающую переходную характеристику: ), получаем линейно возрастающую переходную характеристику: Для того, чтобы найти импульсную характеристику, вспомним, что интеграл от дельта-функции на любом интервале, включающем  , равен 1. Поэтому , равен 1. Поэтому  (при (при  ). ). Рисунок 8 – Переходная и импульсная характеристики. Частотная характеристика интегрирующего звена определяется формулой  . Можно показать, что его логарифмическая амплитудная частотная характеристика – это прямая с наклоном − 20 дБ/дек. На низких частотах усиление максимально, теоретически на частоте . Можно показать, что его логарифмическая амплитудная частотная характеристика – это прямая с наклоном − 20 дБ/дек. На низких частотах усиление максимально, теоретически на частоте  оно равно бесконечности. Высокие частоты, наоборот, подавляются интегратором. оно равно бесконечности. Высокие частоты, наоборот, подавляются интегратором.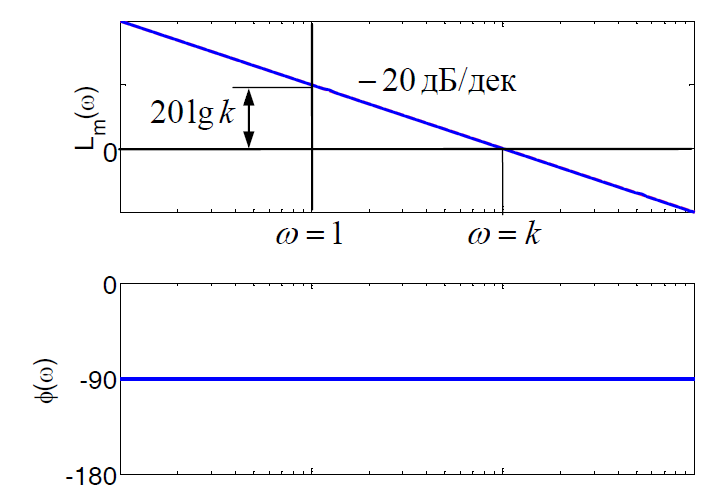 Рисунок 9 – ЛАЧХ и ЛФЧХ интегрирующего звена. На частоте 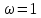 значение ЛАЧХ равно значение ЛАЧХ равно 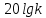 , а при , а при 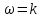 ЛАЧХ обращается в нуль, поскольку ЛАЧХ обращается в нуль, поскольку  . Фазовая характеристика . Фазовая характеристика  – говорит о постоянном сдвиге фазы на всех частотах. – говорит о постоянном сдвиге фазы на всех частотах.2.6 Реально дифференцирующее звеноВстречаются звенья, которые реагируют только на скорость изменения входного сигнала. Такие звенья называются реально дифференцирующими и описываются следующим уравнением:  , где , где — входная величина; — входная величина; — выходная величина, — выходная величина, — постоянная времени, характеризующая инерционность процессов, протекающих в звене, — постоянная времени, характеризующая инерционность процессов, протекающих в звене, — коэффициент передачи. — коэффициент передачи.Примером такого звена является RC-цепочка:  Рисунок 10 – RC-цепочка. Формула передаточной функции:  Частотные характеристики, а их графики приведены ниже: АФХ:  ; ;АЧХ:  ; ;ФЧХ:  . .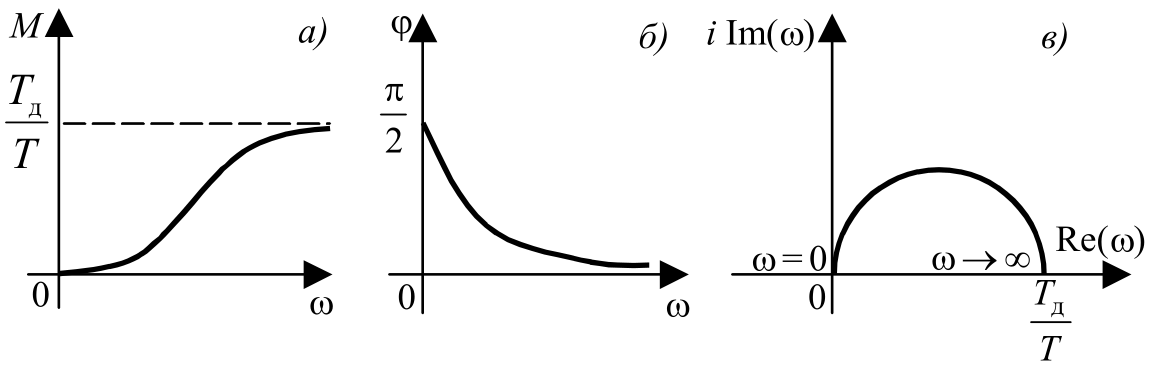 Рисунок 11 – частотные характеристики реального дифференцирующего звена, где а) – АЧХ, б) – ФЧХ, в) – АФХ. Из приведённых графиков об их поведении можно сделать следующие выводы: Верхний предел АЧХ реально дифференцирующего звена ограничен величиной, равной 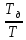 ; ;При увеличении частоты ФЧХ уменьшается от 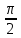 до 0; до 0;Для положительных частот АФХ является полуокружностью с 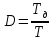 со следующей координатой центра со следующей координатой центра 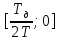 . .Уравнение переходной функции в операторной форме можем получить следующим образом: 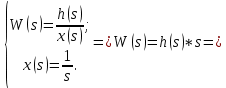 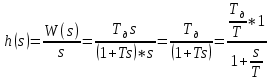 Чтобы получить переходную функцию во временной области необходимо применить обратное преобразование Лапласа к предыдущей формуле: 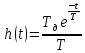 Весовая же функция находится путём взятия производной от  : : Графики переходных функций можно увидеть ниже.  Рисунок 12 – переходные характеристики реального дифференцирующего звена, где а) – переходная функция, б) – весовая функция. Ход работы3.1 Апериодическое звеноПостроим модель апериодического звена и выведем графики для различных характеристик.  Рисунок 13 – Модель апериодического звена  Рисунок 14 – Переходная характеристика апериодического звена h(t)  Рисунок 15 – Импульсная характеристика апериодического звена w(t)  Рисунок 16 – Синусоидальных сигнал апериодического звена  Рисунок 17 – Диаграмма Боде 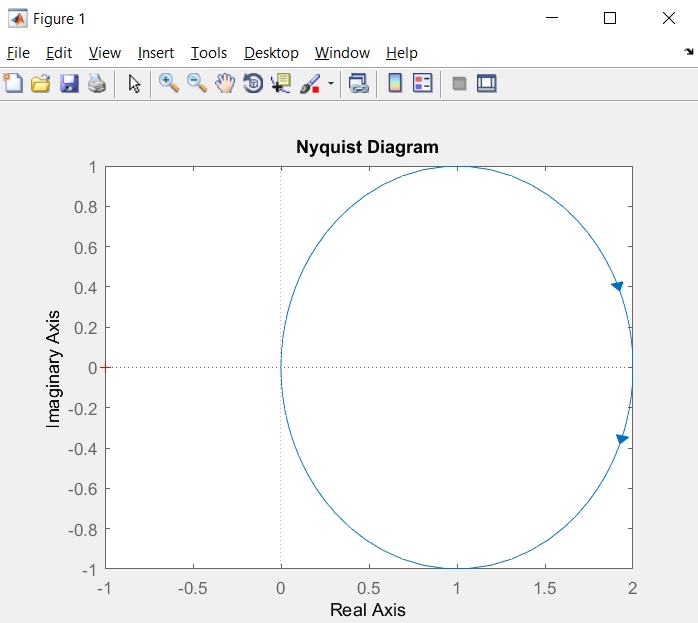 Рисунок 18 – Диаграмма Найквиста 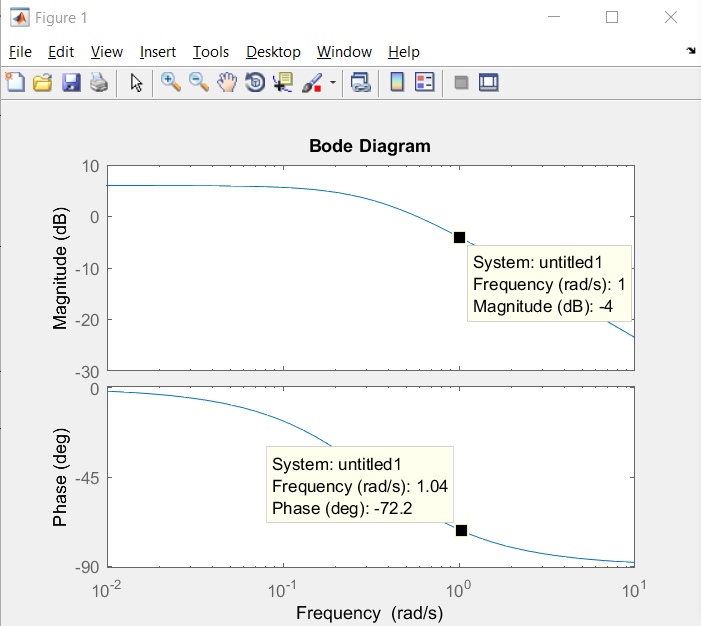 Рисунок 19 – Точки, взятые для сравнения Разница -1,25 радиан (примерно -71 градус), что соответствует диаграмме Боде при частоте 1 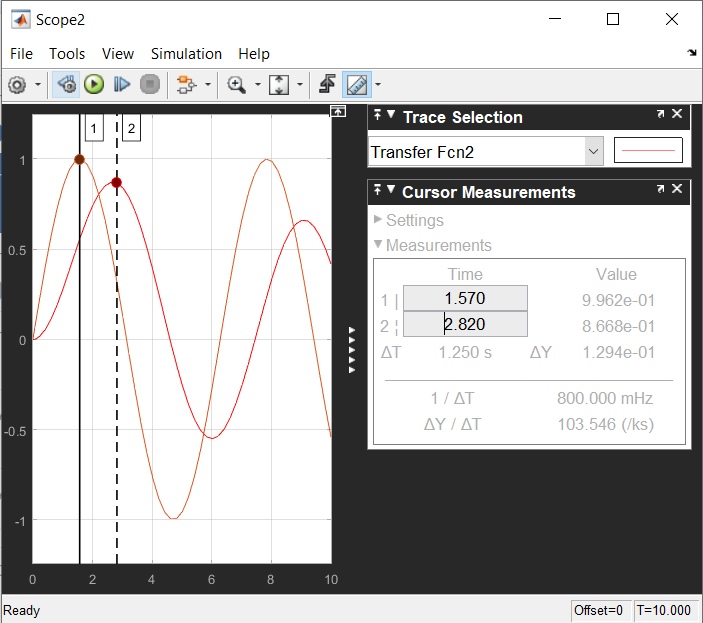 Рисунок 20 – Сравнение 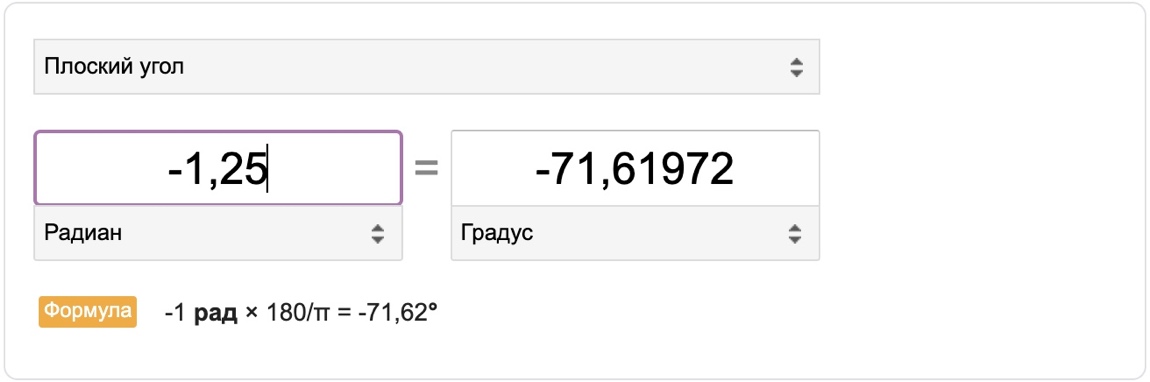 Рисунок 21 – Перевод значения из радиан в градусы 3.2 Дифференцирующее звено Рисунок 22 – Переходная характеристика дифференцирующего звена  Рисунок 23 – Импульсная характеристика дифференцирующего звена  Рисунок 24 – Синусоидальный сигнал дифференцирующего звена Из графика видно разницу между двумя сигналами: амплитуда та же, а фаза на 1.567 рад = 90 град сместилась, что подтверждается диаграммой боде. 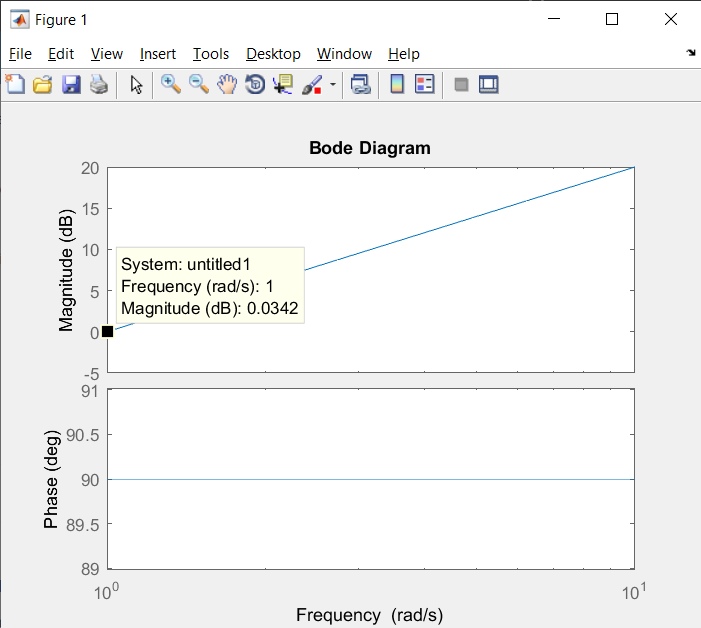 Рисунок 25 – Диаграмма боде для дифференцирующего звена при частоте 1 Колебательное звеноКолебательное звено – это звено второго порядка с передаточной функцией вида:  Знаменатель которой имеет комплексно-сопряженные корни (то есть,  ). ). Рисунок 26 – Схема переходной функции.  Рисунок 27 – График переходной функции. 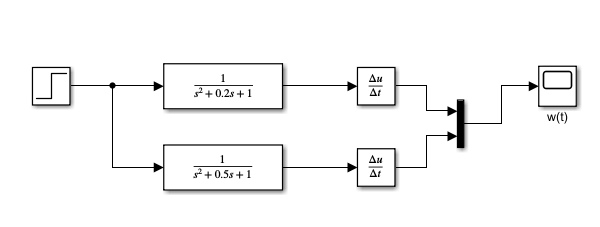 Рисунок 28 – Схема импульсной характеристики. 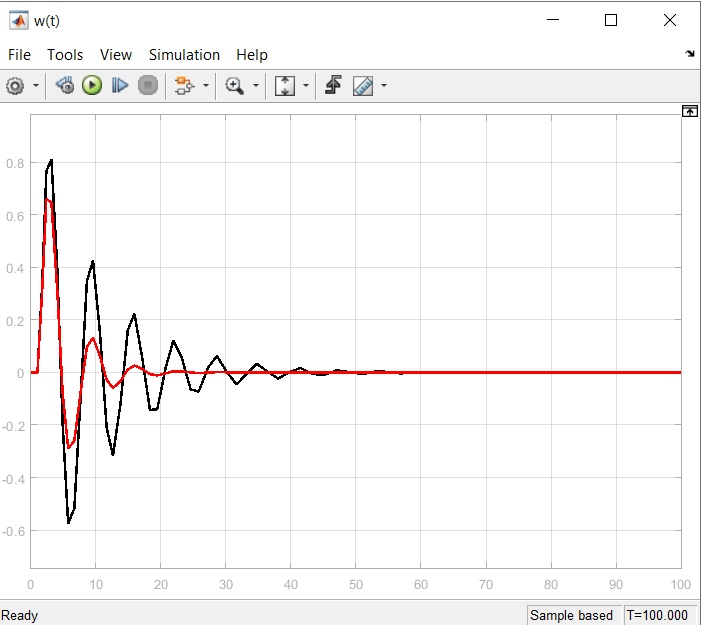 Рисунок 29 – График импульсной характеристики. 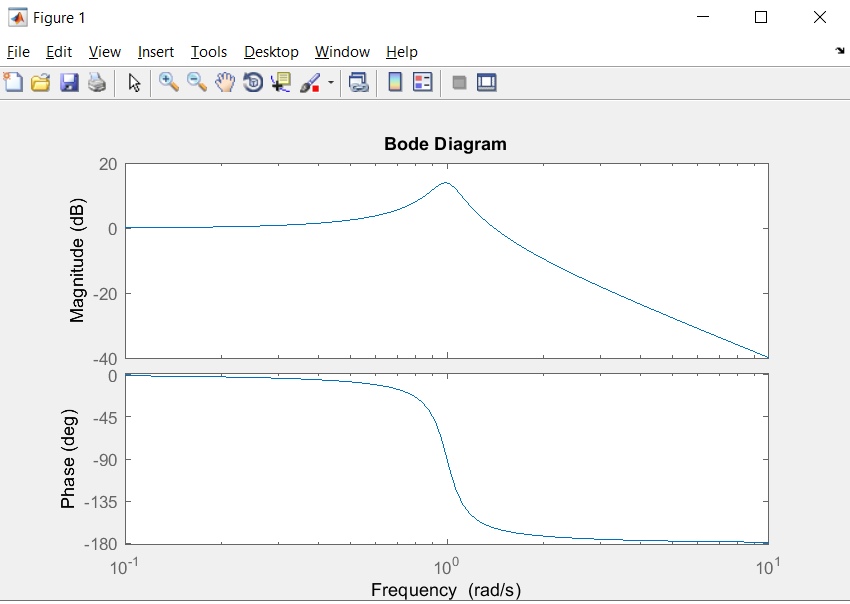 Рисунок 30 – АЧХ и ФЧХ. 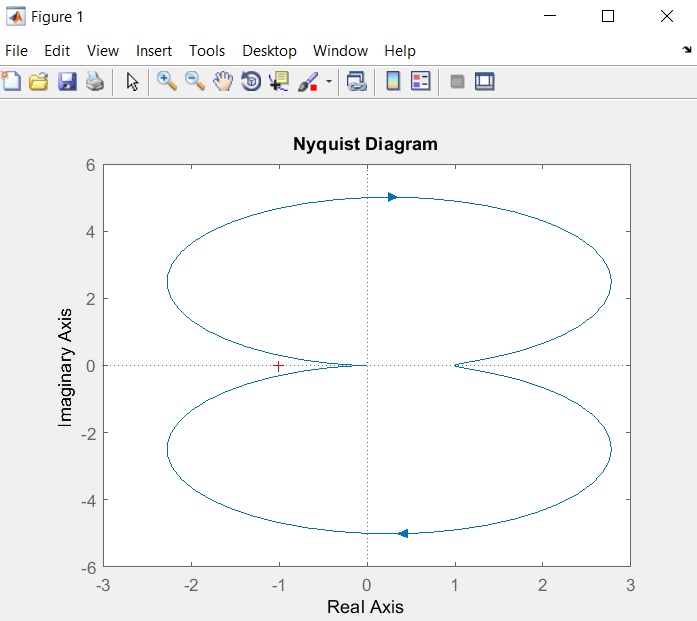 Рисунок 31 – График диаграммы Найквиста. Усилительное звеноУсилительное звено – это звено, для которого в любой момент времени выходная величина пропорциональна. Исследуем свойства модели усилителя: Его передаточная функция W(s) = k. При действии на вход единичного ступенчатого сигнала 1(t) (или дельта – функции  ) на выходе будет такой же сигнал, усиленный в k раз, поэтому переходная и импульсная характеристики звена равны h(t) = k (t>0) и w(t)=k* ) на выходе будет такой же сигнал, усиленный в k раз, поэтому переходная и импульсная характеристики звена равны h(t) = k (t>0) и w(t)=k* . .Если на вход усилителя действует синусоидальный сигнал, на выходе он усиливается в k раз без изменения фазы, поэтому амплитудная и фазовая частотная характеристики не зависят от частоты входного сигнала:   Рисунок 32 – Схема усилителя.  Рисунок 33 – Переходная характеристика усилителя.  Рисунок 34 – Схема усилителя (дельта-сигнал).  Рисунок 35 – Переходная характеристика усилителя (дельта-сигнал).  Рисунок 36 – Импульсная характеристика усилителя.  Рисунок 37 – АЧХ и ФЧХ усилителя. 3.5 Интегрирующее звеноПостроим модель интегрирующего звена и выведем графики для различных характеристик.  Рисунок 38 – Модель интегрирующего звена.  Рисунок 39 – Переходная характеристика интегрирующего звена.  Рисунок 40 – Импульсная характеристика интегрирующего звена.  Рисунок 41 – ЛАЧХ (Диаграмма Боде) интегрирующего звена.  Рисунок 42 – Диаграмма Найквиста интегрирующего звена. 3.6 Реально дифференцирующее звеноПостроим модель реального дифференцирующего (РД) звена для 2-х переходных функций  , , и выведем графики для различных характеристик. и выведем графики для различных характеристик. Рисунок 43 – Модель реального дифференцирующего звена.  Рисунок 44 – Переходная характеристика  РД звена. РД звена. Рисунок 45 – Переходная характеристика  РД звена. РД звена. Рисунок 46 – Амплитудно-частотная характеристика  РД звена. РД звена. Рисунок 47 – Амплитудно-частотная характеристика  РД звена. РД звена. Рисунок 48 – ЛАЧХ  (диаграмма Боде) РД звена. (диаграмма Боде) РД звена. Рисунок 49 – ЛАЧХ  (диаграмма Боде) РД звена. (диаграмма Боде) РД звена. Рисунок 50 – Диаграмма Найквиста для  . . Рисунок 51 – Диаграмма Найквиста для 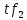 . .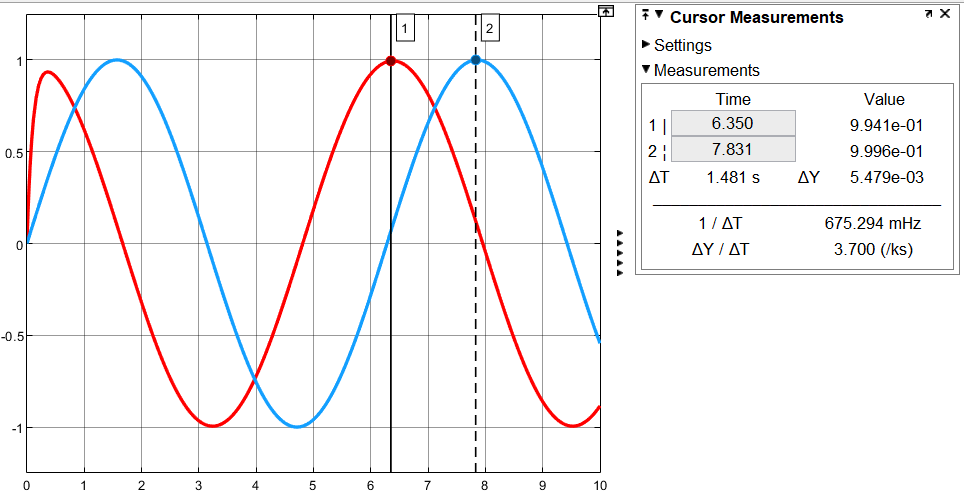 Рисунок 52 – Сравнение графиков по синусоидальной характеристики для 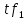 . .Фаза составила 1.481 рад, что равняется 84.85° и примерно равно значению 84.3°. 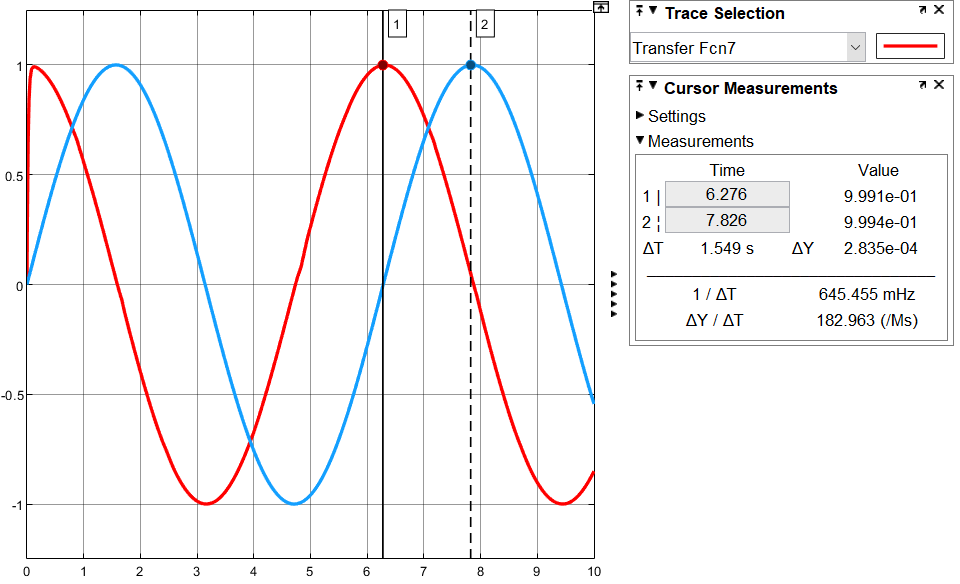 Рисунок 53 – Сравнение графиков по синусоидальной характеристики для 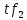 . .Фаза составила 1.549 рад, что равняется 88,75° и примерно равно значению 88.8°. ВыводВ ходе лабораторной работы были изучены динамические характеристики типовых звеньев систем автоматического управления и их вид в системе Matlab/Simulink. Новосибирск 2021 |
