Лабораторная работа 1. Лабораторная работа 1 По предмету "Теория вероятности и математическая статистика"
 Скачать 1.79 Mb. Скачать 1.79 Mb.
|
|
МИНИСТЕРСТВО ПО РАЗВИТИЮ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И КОММУНИКАЦИЙ РЕСПУБЛИКИ УЗБЕКИСТАН ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ имени МУХАММАДА АЛЬ-ХОРЕЗМИ ЛАБОРАТОРНАЯ РАБОТА №1 По предмету: “Теория вероятности и математическая статистика” Выполнил: студент 2 курса гр. MTH202-L2 факультета Программный инжиниринг Исмагилов Д.Р Ташкент-2022 Тема: Случайные события и их вероятности. Вероятность сложных событий (условная вероятность, полная вероятность и формула Байеса). Цель лабораторной работы: Научится о предмет случайные события и их вероятности. Умение применять условную вероятность, полную вероятность и формулы Байеса. Необходимая информация и инструкция: Событие –это факт, который происходит в результате наблюдения или опыта. Обычно события происходят при соблюдении определённых условий или в результате эксперимента. Вероятность события-это отношение количества результатов испытания способствующих возникновению события, к общему количеству равновозможных, несовместных элементарных результатов испытания и определяется по следующей формуле 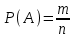 Конечно, чтобы это определение имело смысл, пространство элементарных событий должно быть конечным и все результаты эксперимента должны быть в равной опытами возможными. Относительная частота события-это отношение количества испытаний, в которых произошло событие, к общему количеству фактически проведённых испытаний, которое определяется по следующей формуле: 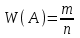 Где m-количество испытаний с благоприятным исходом, n-общее количество испытаний. Геометрическая вероятность события. 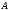 -это отношение измерения области D к измерению области G. -это отношение измерения области D к измерению области G.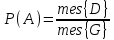 , ,Здесь mes-означает длину, площадь или объём. Теорема-1. Вероятность того, что два связанных события происходят вместе, равна умножению вероятности одного из них на условную вероятность другого. Первое событие вычисленную при условии, что первое имело место: 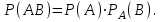 Теорема-2. Общая вероятность того, что события 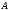 произойдёт ,только если произойдёт одно из несовпадающих событии составляющих полную группу, равна сумме вероятностей каждого из этих событии, умноженных на соответствующую вероятность события произойдёт ,только если произойдёт одно из несовпадающих событии составляющих полную группу, равна сумме вероятностей каждого из этих событии, умноженных на соответствующую вероятность события 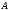 . .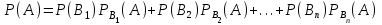 . .Предположим, что проведём испытание, в результате которого произошло событие 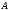 .Ставим задачу, определить, как изменились вероятности гипотез, если события .Ставим задачу, определить, как изменились вероятности гипотез, если события 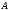 произошло. Другими словами, мы ищем условные вероятности произошло. Другими словами, мы ищем условные вероятности 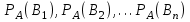 . .Сначала находим условную вероятность. На основании теоремы умножения получаем: 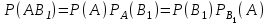 . .Отсюда, 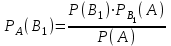 . .Подставляя в это отношение Р( 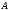 ) получаем ) получаем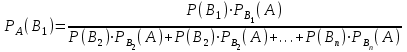 . .Формулы для определения условных вероятностей остальных гипотез задаются аналогичным образом, т.е. условные вероятности произвольной гипотезы 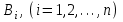 могут быть вычислены по следующие формуле. могут быть вычислены по следующие формуле.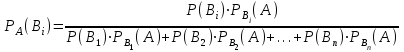 . .Полученные формулы (названные в честь английского математика, придумавшего их в 1764 году) называются формулами Байеса. Эти формулы позволяют переоценить вероятности гипотез после того, как станет известно, что событие произошло в результате испытания. Задачи выполняемые в лабораторным занятиях: 1.Измените все параметры в задаче на номер варианта и перепишите условие задачи (где V-номер вариант). 2.Определите эксперименты и случайные события. 3.Отличить событие “А” от других исследуемых событий. 4.Напишите необходимые формулы для расчёта и производите расчёты на калькуляторе. Выполнение задания:          Вывод: В данной лабораторной работе изучили основные определения классической вероятности. Узнали, что такое событие и какие они бывают. Изучили теоретическую часть (статистическая вероятность, геометрическая вероятность, условная вероятность и полная вероятность). Решили 8 задач по варианту 6 (номер варианта взят из журнала). Решение и результат задач решены и получены в тетради. Следовательно, в лабораторную работу добавили изображений из тетради с решениями задач. |
