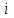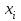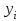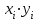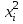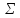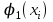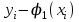Лабораторная работа 1 по теме Методы решения нелинейных уравнений

• Название: Лабораторная работа 1 по теме Методы решения нелинейных уравнений
• Дата: 31.03.2023
• Размер: 386.38 Kb.
• Имя файла: NLU_Interp_MNK_LAB (1).docx
• Тип: Лабораторная работа; #1028845
• страница: 4 из 4

3.4. Содержание отчета

1. 
   Индивидуальное задание.
   
2. 
   Линейная аппроксимация:
   

• 
  значения элементов матрицы Грамма и столбцов свободных членов, представленные в табл. 3-3:
  

Таблица 3-3

0
1
2
3
4
5

• 
  системы нормальных уравнений и их решения, аппроксимирующие функции;
  
• 
  исходная функция и результаты аппроксимации в узловых точках, представленные в табл. 3-4:
  

Таблица 3-4

• 
  оценка погрешности (среднеквадратическое отклонение).
  

3. 
   Аппроксимация с помощью математического пакета.
   

3.5. Пример выполнения задания

1. 
   Задание для решения задачи аппроксимации
   

Для решения задачи аппроксимации методом наименьших квадратов выберем функцию y(x), заданную следующей таблицей:

	1.0	1.2	1.4	1.6	1.8	2.0
	0.634	2.44	3.326	2.926	2.24	2.634

2. 
   Линейная аппроксимация:
   

Вычислить и записать в табл. 3-3 элементы матрицы Грамма и столбец свободных членов:

0	1.0	0.634	0.634	1
1	1.2	2.44	2.928	1.44
2	1.4	3.326	4.6564	1.96
3	1.6	2.926	4.6816	2.56
4	1.8	2.24	4.032	3.24
5	2.0	2.634	5.268	4
	9	14.2	22.2	10.2

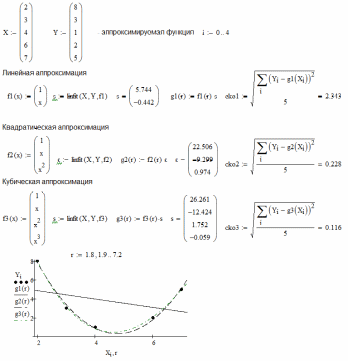
составить системы нормальных уравнений:

для линейной функции P1(x) = А0+А1*x система нормальных уравнений примет вид (линейная аппроксимация):
6*А0+9*А1 = 14.2

9*А0+10.2*А1 = 22.2
решить систему уравнений:

получим коэффициенты А0 = 0.438 и А1 = 1.286, тогда полином первой степени будет таким:
P1(x) = 0.438+1.286*x

3. 
   Аппроксимация с помощью математического пакета
   

Осуществить аппроксимацию таблично заданной функции многочленом 1, 2, 3, 4 и 5-й степени.

В этом примере рассмотрено использование функции linfit(x,y,f), где x,y- соответственно векторы значений аргументов и функции, а f – символьный вектор базисных функций. Использование этой функции позволяет определить вектор коэффициентов аппроксимации методом наименьших квадратов и далее невязку - среднеквадратическую погрешность приближения исходных точек к аппроксимирующей функции (сkо). Степень аппроксимирующего многочлена задается при описании символьного вектора f. В примере представлена аппроксимация таблично заданной функции многочленом 1, 2, 3, 4, 5-й степени, . Вектор s представляет собой набор аппроксимирующих коэффициентов, что позволяет получить аппроксимирующую функцию в явном виде.

Следует построить графики для полиномов 1, 2 и 5 степени.

Проанализировать изменение СКО в зависимости от степени полинома.