ИМЭС Лабораторная работа. имэс лб1. Лабораторная работа 1 Подготовительная часть (Задача об ассортименте продукции.)
 Скачать 194.1 Kb. Скачать 194.1 Kb.
|
|
Лабораторная работа №1 Подготовительная часть (Задача об ассортименте продукции.) Фирма XYZ выпускает три вида продукции (изделий). В процессе производства используются три технологические операции. На рис. 1 показана технологическая схема производства изделий видов 1, 2 и 3. При изготовлении изделия 2 технологическая операция 2 не выполняется, а при производстве изделия 3 используются только технологические операции 1 и 2. 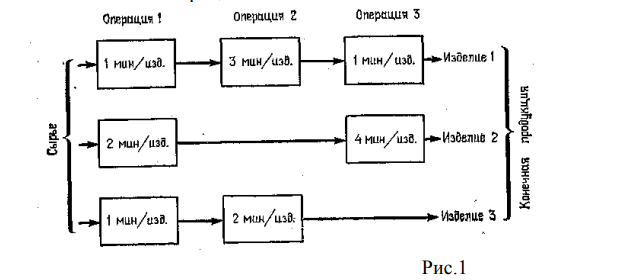 В прямоугольниках на рис.1 указана длительность технологических операций при изготовлении одного изделия каждого вида. Так как эти технологические операции используются фирмой и для других производственных целей, фонд рабочего времени, в течение которого операции 1, 2 и 3 могут быть применены для производства рассматриваемых изделий, ограничен следующими предельными значениями (в сутки); для первой операции —430 мин, для второй операции —460 мин, для третьей операции —420 мин. Изучение рынка сбыта показало, что ожидаемая прибыль от продажи одного изделия видов 1, 2 и 3 составляет 3, 2 и 5 долл. соответственно. Каков наиболее выгодный суточный объем производства каждого вида продукции? Математическая модель: 3x1+2x2+5x3 -> max x1+2x2+x3<=430 3x1+2x3<=460 x  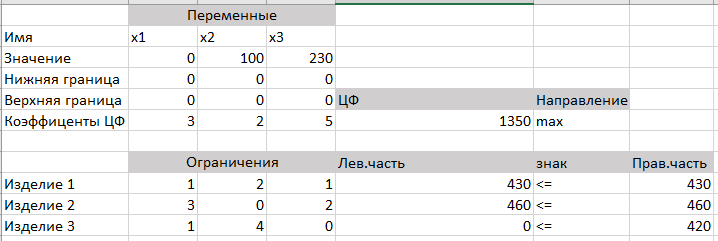 1+4x2<=420 1+4x2<=420Значения 0,100,230 Ответ: 1350 Бройлерное хозяйство птицеводческой фермы насчитывает 20 000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки .поступают в продажу. Хотя недельный расход корма для цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 ед. Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов. Обычно перечень ингредиентов достаточно широк, но для того, чтобы проиллюстрировать процесс построения модели, ограничимся только тремя ингредиентами: известняком, зерном и соевыми бобами. Требования к питательности рациона сформулируем также в упрощенном виде, учитывая только три вида питательных веществ: кальций, белок и клетчатку. В таблице приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента. Заметим, что известняк не содержит ни белка, ни клетчатки. Ингредиент Содержание питательных веществ, кг/(кг ингредиента) Стоимость, долл. кальций белок клетчатку /кг Известняк 0,38 0,04 Зерно 0,001 0,09 0,02 0,15 Соевые бобы 0,002 0,50 0,08 0,40 Смесь должна содержать: 1)не менее 0,8%, но не более 1,2% кальция; 2) не менее 22% белка; 3)не более 5% клетчатки. Математическая модель задачи: 0,04x1+0,15x2+0,4x3→min Ограничения: 0,38x1 +0,001x2 + 0,002x3 ≤ 1280 0,38x1 + 0,001x2 + 0,002x3 ≥ 1920 0,09x2 + 0,5x3 ≥ 35200 0,02x2 + 0,08x3 ≤ 8000 x1, x2, x3 ≥ 0 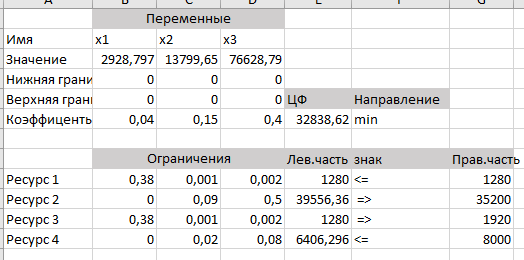 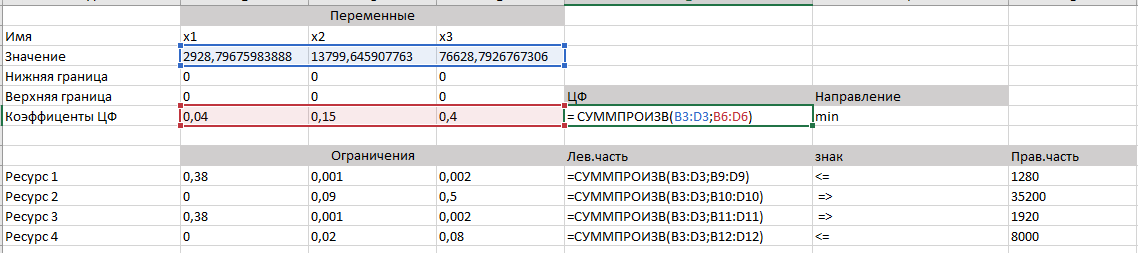 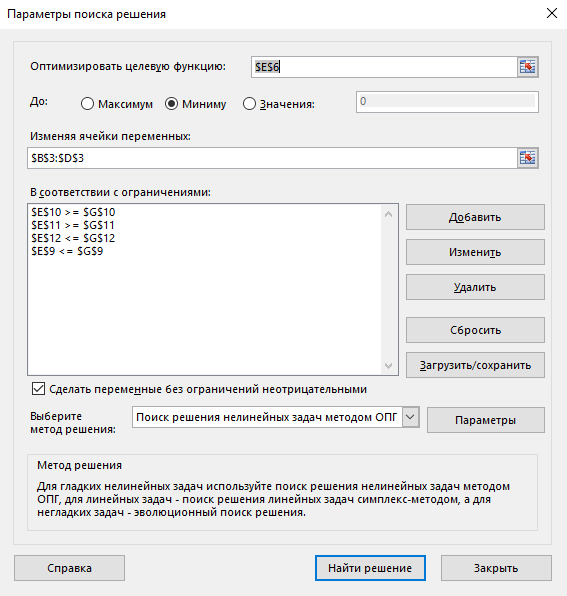 Ответ: 32838 Исследуются возможности более рациональной организации работы городского автобусного парка с целью снижения интенсивности внутригородского движения. На начальном этапе исследования было определено минимальное количество автобусов, которым можно удовлетворить существующую потребность в пассажирских перевозках. Сбор и обработка необходимой информации позволили сделать вывод, что минимальное количество автобусов, которым можно удовлетворить потребности в перевозках, существенно меняется в течение суток. При дальнейшем анализе было обнаружено, что требуемое количество автобусов можно считать величиной постоянной в пределах каждого из следующих; друг за другом четырехчасовых интервалов (рис.2). В результате проведенного исследования было решено, что с учетом необходимых затрат времени на текущий ремонт и обслуживание непрерывное использование автобусов на линии должно продолжаться только по 8 ч в сутки. Рис.2. Требуется определить количество автобусов в каждой из смен, которое должно быть не меньше минимальной потребности в них, при условии что общее количество автобусов, выходящих на линию в течение суток, будет минимальным. Математическая модель задачи: x1+ x2 + x3 + x4 + x5+ x6 → min Ограничения: x6+x1 ≥ 4 x1+x2 ≥ 8 x2+x3 ≥ 10 x3+x4 ≥ 7 x4+x5 ≥ 12 x5+x6 ≥ 4 x1…6 – целые 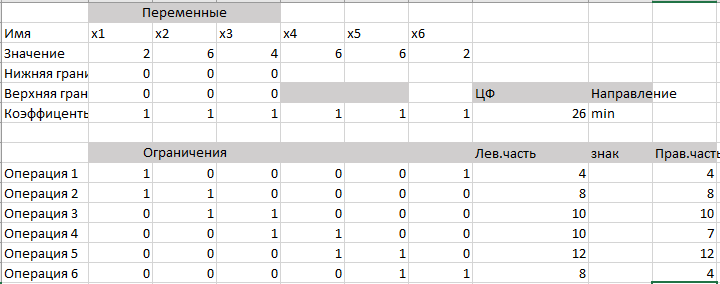  Ответ: 26 |
