Лабораторные. Лабораторная работа 1 предполагает сбор (с сайта Росстата) и оформление в виде таблиц данных по следующим показателям

• Название: Лабораторная работа 1 предполагает сбор (с сайта Росстата) и оформление в виде таблиц данных по следующим показателям
• Дата: 01.09.2022
• Размер: 204.78 Kb.
• Имя файла: Лабораторные.docx
• Тип: Лабораторная работа; #658922
• страница: 1 из 4

Лабораторная работа 1

Сбор статистических данных. Построение корреляционных матриц
Количество показателей: 6.

Количество наблюдений (выборка): не менее 25 наблюдений (если временная выборка – лет; если пространственная – кол-во изучаемых регионов).
Лабораторная работа 1 предполагает сбор (с сайта Росстата) и оформление в виде таблиц данных по следующим показателям.

1) Студент выбирает исследуемый регион РФ и собирает статистические данные по показателям:

1. Валовой региональный продукт (ВРП)

2. Инвестиции в основной капитал

3. Стоимость основных фондов

4. Численность рабочей силы

5. Среднегодовая численность занятых

6. Затраты на технологические инновации

Полученные данные оформляет в виде таблиц.

2) строит корреляционные матрицы (которые включают попарные коэффициенты как абсолютных величин, так и темпов роста всех исследуемых показателей).

3) результаты лабораторной работы оформляет в формате doc. или docx. Вносит в документ исходные данные, показывает полученный результат и его интерпретирует – делает выводы.
Исследуемый регион – Белгородская область.

Таблица 1 - Статистические данные

Год	ВРП млн. руб.	Инвестиции в основной капитал, млн. руб.	Стоимость основных фондов, млн. руб.	Численность рабочей силы, тыс. чел.	Среднегодовая численность занятых, тыс. чел.	Затраты на технологические иновации, млн. руб.
	Y	X1	X2	X3	X4	X5
1998	18 245,5	8965	132564	735	661,5	121,8
1999	32 060,6	9110	149876	739	665,1	126,2
2000	42 074,5	9242	154391	741	671,3	139,2
2001	49 941,8	14031	173840	748	677,5	969,1
2002	62 404,4	10830	214329	720	673,4	1026,6
2003	76 054,5	15336	247369	718	668,3	884,0
2004	114 409,3	22685	264218	734	670,7	400,0
2005	144 987,8	35022	295272	715	674,7	1204,6
2006	178 846,1	52073	332176	756	677,4	734,6
2007	237 013,3	83510	425857	732	685,3	799,1
2008	317 656,3	104218	507024	761	695,3	1213,6
2009	304 345,3	73127	586006	791	693,0	1197,8
2010	398 361,4	96313	671563	779	749,8	3072,3
2011	507 839,8	125994	797428	767	759,7	2136,6
2012	545 517,2	136820	921456	787	780,1	1629,0
2013	569 006,4	129405	1035534	810	774,0	1107,4
2014	619 677,7	120658	1152400	814	764,5	4108,8
2015	693 379,4	147214	1289717	806	754,0	2392,9
2016	778 027,8	143792	1400837	822	756,8	20339,0
2017	837 306,8	142693	1501847	824	757,9	23852,4
2018	911 597,9	134551	1564553	825	752,6	20703,2
2019	955 329,2	167093	2858983	826	754,1	30653,0
2020	999 081,6	168123	2928570	834	751,9	21540,9
2021	1 270 000,0	165671,7	2999851	842	749,7	25334,5

Зависимая переменная:

Y - Валовой региональный продукт (ВРП).

Независимые переменные:

Х1 - Инвестиции в основной капитал;

Х2 - Стоимость основных фондов;

Х3 - Численность рабочей силы;

Х4 - Среднегодовая численность занятых;

Х5 - Затраты на технологические инновации.

Строим матрицу парных коэффициентов корреляции для абсолютных величин.

Матрица коэффициентов корреляции в Excel строится с помощью инструмента «Корреляция» из пакета «Анализ данных».
Таблица 2 – Матрица парных коэффициентов корреляции для абсолютных величин

	Y	X1	X2	X3	X4	X5
Y	1
X1	0,9362262	1
X2	0,9449461	0,8433041	1
X3	0,9360088	0,901096	0,861464	1
X4	0,8348294	0,9141123	0,6938715	0,8523058	1
X5	0,8517203	0,6948095	0,8862997	0,7679008	0,5429198	1

Качественная характеристика связи дается на основе коэффициента корреляции по шкале Чеддока.

Таблица 3. Шкала Чеддока

Коэффициент корреляции	0,1 — 0,3	0,3 — 0,5	0,5 — 0,7	0,7 — 0,9	0,9 — 0,99
Связь…	слабая	умеренная	заметная	высокая	весьма высокая

Строим матрицу парных коэффициентов корреляции для базисных темпов роста исследуемых показателей.

Т_рб = Выбранный показатель / Базовый показатель * 100 %

Таблица 4. Базисные темпы роста исследуемых показателей, %

Y	X1	X2	X3	X4	X5
-	-	-	-	-	-
175,7	101,6	113,1	100,5	100,5	103,6
230,6	103,1	116,5	100,8	101,5	114,3
273,7	156,5	131,1	101,8	102,4	795,6
342,0	120,8	161,7	98,0	101,8	842,9
416,8	171,1	186,6	97,7	101,0	725,8
627,1	253,0	199,3	99,9	101,4	328,4
794,6	390,7	222,7	97,3	102,0	989,0
980,2	580,9	250,6	102,9	102,4	603,1
1299,0	931,5	321,2	99,6	103,6	656,1
1741,0	1162,5	382,5	103,5	105,1	996,4
1668,1	815,7	442,1	107,6	104,8	983,4
2183,3	1074,3	506,6	106,0	113,3	2522,4
2783,4	1405,4	601,5	104,4	114,8	1754,2
2989,9	1526,2	695,1	107,1	117,9	1337,4
3118,6	1443,4	781,2	110,2	117,0	909,2
3396,3	1345,9	869,3	110,7	115,6	3373,4
3800,3	1642,1	972,9	109,7	114,0	1964,6
4264,2	1603,9	1056,7	111,8	114,4	16698,7
4589,1	1591,7	1132,9	112,1	114,6	19583,3
4996,3	1500,9	1180,2	112,2	113,8	16997,7
5236,0	1863,8	2156,7	112,4	114,0	25166,6
5475,8	1875,3	2209,2	113,5	113,7	17685,5
6960,6	1848,0	2262,9	114,6	113,3	20800,1

Таблица 5 – Матрица парных коэффициентов корреляции для базисных темпов роста исследуемых показателей

	Y	X1	X2	X3	X4	X5
Y	1
X1	0,9322716	1
X2	0,9436257	0,8381068	1
X3	0,9332627	0,8977647	0,8557753	1
X4	0,823329	0,906887	0,6792837	0,845447	1
X5	0,8511592	0,6894428	0,8842702	0,7625516	0,5293247	1

Выводы

Анализ первого столбца матрицы (таблица 2) позволяет произвести отбор факторных признаков, которые могут быть включены в модель множественной корреляционной зависимости. Факторные признаки, у которых 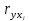< 0.5 исключают из модели.

В нашем случае все для всех факторов выполняется условие 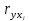> 0.5.

Если рассматривать в качестве зависимой переменной Y параметр «валовой региональный продукт (ВРП)», а остальные параметры - независимые переменные X_i, то можно сказать, что наиболее тесная связь наблюдается между ВРП и Стоимостью основных фондов 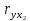= 0.945.

Значимость парных коэффициентов корреляции проверяют по t–критерию Стьюдента. Выдвигается гипотеза о равенстве нулю генерального коэффициента корреляции: H₀ :ρ=0. Затем задаются параметры: уровень значимости α и число степеней свободы ν = n − 2. Вычисляют tkp=СТЬЮДЕНТ.ОБР.2Х(0,05;22) = 2,07

По имеющимся данным вычисляют наблюдаемое значение критерия: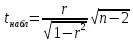


Таблица 6 – Наблюдаемые значения критерия:

	Y	X1	X2	X3	X4	X5
Y	1
X1	11,91507	1
X2	12,9144	7,017329	1
X3	11,89272	9,293451	7,586537	1
X4	6,781855	10,08244	4,309253	7,287397	1
X5	7,269147	4,320508	8,558731	5,361106	2,891231	1

Парный коэффициент корреляции считается значимым (гипотеза о равенстве коэффициента нулю отвергается) с доверительной вероятностью γ = 1−α = 0,95, если по модулю t_набл будет больше, чем t_кр. Для нашего случая все парные коэффициенты корреляции – значимы.

Если в матрице есть межфакторный коэффициент корреляции 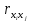> 0,7, то в данной модели множественной регрессии существует мультиколлинеарность.

Для наших данных можно сказать, что только факторы х₄ и х₅ не мультиколлинеарны. Между остальными факторами наблюдается заметная, высокая и весьма высокая связь.