Лабораторные. Лабораторная работа 1 предполагает сбор (с сайта Росстата) и оформление в виде таблиц данных по следующим показателям
 Скачать 204.78 Kb. Скачать 204.78 Kb.
|
Лабораторная работа 4Проверка парной линейной регрессии, построенной в Лаб.2, на автокорреляцию (если выборка временная) или на гетероскедастичность (если выборка пространственная) Количество показателей: три или более. Количество наблюдений (выборка): не менее 22. 1) Студент дает определение автокорреляции / гетероскедастичности. Раскрывает вероятные причины ее возникновения. 2) Построенную в Лабораторной работе 2 парную линейную регрессию студент проверяет на наличие автокорреляции при помощи теста Дарбина-Уотсона. Делает выводы. Или же построенную в Лабораторной работе 2 парную линейную регрессию проверяет на наличие гетероскедастичности при помощи теста Голфелда-Квандта. Делает выводы о гетероскедастичности или гомоскедастичности остатков. Выборка временная – проверяем на автокорреляцию Автокорреляция Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями. Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных. В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов. Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето). Среди основных причин, вызывающих автокорреляцию, можно выделить следующие: 1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию. 2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью. 3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом). 4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции. Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными. Под гетероскедастичностью понимается предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, что означает нарушение второго условия нормальной линейной модели множественной регрессии. Под гомоскедастичностью понимается предположение о том, что дисперсия случайной ошибки βi является известной постоянной величиной для всех наблюдений. Но на практике предположение о гомоскедастичности случайной ошибки βi или остатков модели регрессии ei выполняется не всегда. Существует много причин, по которым гетероскедастичность может возникать в регрессионных моделях, но обычно это связано с проблемами с набором данных. Показано, что модели, использующие широкий диапазон значений, более подвержены гетероскедастичности, поскольку различия между наименьшими и наибольшими значениями очень значительны. Гетероскедастичность часто наблюдается в финансовых временных рядах с высокой периодичностью (дневные и внутридневные данные). Имеются в виду биржевые котировки. Гетероскедастичность для этих данных обусловлена тем, что в зависимости от режима, в котором функционирует рынок, дисперсия котировок может сильно отличаться. Так появление новой негативной или позитивной информации может вызвать сильное увеличение дисперсии. Кроме того, смена состояний рынка происходит постепенно, поэтому дисперсия будет зависеть от своих значений в предыдущие периоды времени. Большие объемы данных, которые доступны при анализе финансовых временных рядов (число наблюдений измеряется тысячами), позволяют оценивать сложные модели гетероскедастичности, которые учитывают не симметричное влияние позитивных и негативных шоков, а то, что реакция на шоки не пропорциональная и т.д Гетероскедастичность остатков модели регрессии может привести к негативным последствиям: 1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности; 2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом. Проверка на автокорреляцию Критерий Дарбина-Уотсона. Этот критерий является наиболее известным для обнаружения автокорреляции. Для анализа коррелированности отклонений используют статистику Дарбина-Уотсона: С помощью инструмента Регрессия получим остатки 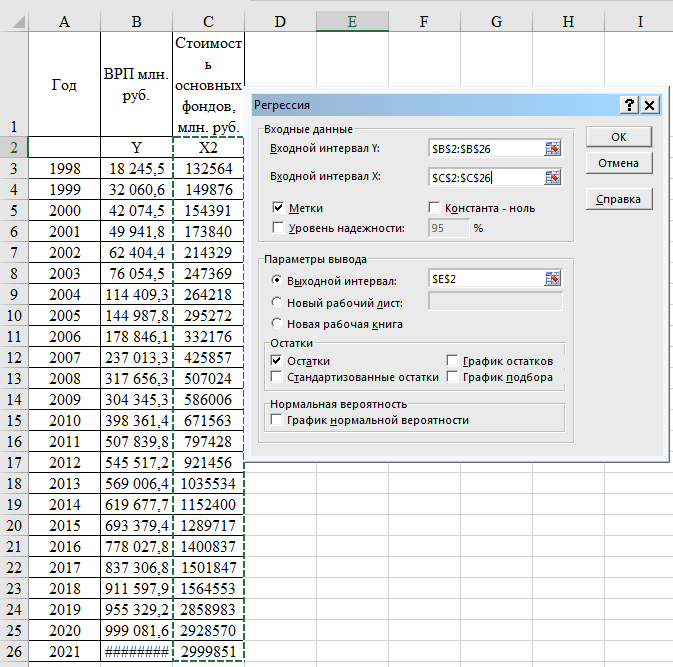
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости α, числа наблюдений n = 24 и количества объясняющих переменных m=1. Автокорреляция отсутствует, если выполняется следующее условие: d1 < DW и d2 < DW < 4 - d2. Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5 < DW < 2.5. Поскольку 1.5 > 0.87 < 2.5, то автокорреляция остатков присутствует. Для более надежного вывода целесообразно обращаться к табличным значениям. По таблице Дарбина-Уотсона для n=24 и k=1 (уровень значимости 5%) находим: d1 = 1.27; d2 = 1.45. Поскольку 1.27 > 0.87 и 1.45 > 0.87 < 4 - 1.45, то автокорреляция остатков присутствует. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
