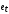Условия. Лекции по омнк на случай автокоррелированных остатков, выполните следующие задания
 Скачать 279.03 Kb. Скачать 279.03 Kb.
|
|
Неделя 27_1 Тема: «Обобщённый метод наименьших квадратов. Эконометрическое моделирование в условиях непостоянства дисперсии ошибок – эффект автокорреляция остатков» Используя материал лекции по ОМНК на случай автокоррелированных остатков, выполните следующие задания. Все решения заданий необходимо оформить в книге Excel. Листы книги называть номером задания. Сам файл с решениями заданий необходимо назвать фамилией студента, выполнившего задания, с пометкой учебной недели, например, «Панов_27_1» и отправить мне на корпоративную почту в срок не позднее 15.03.2021 до 20.00 Задание №1. На основе данных за 5 последовательных лет с применением классического МНК построена модель 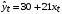 , для которой получены остатки: , для которой получены остатки:
Рассчитать коэффициент автокорреляции остатков и проверить гипотезу о наличие автокорреляции остатков. Сформировать ковариационно-дисперсионную матрицу остатков Ω для применения ОМНК. Задание №2. Для некоторой модели, построенной с применением классического МНК на основе данных за 6 лет, рассчитан коэффициент автокорреляции остатков первого порядка 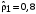 . Определить ковариационно-дисперсионную матрицу остатков Ω для применения ОМНК. . Определить ковариационно-дисперсионную матрицу остатков Ω для применения ОМНК.Задание №3. Для некоторой модели, построенной с применением классического МНК на основе данных за 6 лет, рассчитан коэффициент автокорреляции остатков первого порядка 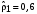 . Определить матрицу весов Р для применения ОМНК. . Определить матрицу весов Р для применения ОМНК.Задание №4. По квартальным данным за 9 лет анализируется зависимость между экспортом ( 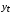 ) и импортом ( ) и импортом (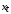 ). Статистические данные приведены в таблице: ). Статистические данные приведены в таблице:
Построить уравнение регрессии текущего импорта на текущий экспорт и константу: 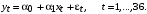 Получите 95% доверительный интервал для оценок регрессии. Проверить качество построенной модели на основе t-статистики и коэффициента детерминации 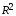 . . Вычислить значение статистики 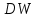 Дарбина-Уотсона, на ее основе определить наличие автокорреляции остатков. Дарбина-Уотсона, на ее основе определить наличие автокорреляции остатков. Допустим известно значение коэффициента автокорреляции первого порядка равное 0,556. Примените ВМНК для оценки коэффициентов модели. Проведите корректировку методом Кохрейна-Оркатта. Сравните качество полученных моделей. Задание №5. По динамическим данным, приведённым в таблице:
Найдите МНК оценки регрессии. Получите 95% доверительный интервал для оценок регрессии. Проанализируйте автокорреляцию остатков. В случае наличия автокорреляции остатков выполнить ее корректировку методом Кохрейна-Оркатта. Задание №6. Исследуется зависимость во времени количества вакансий на 1000 чел. ( 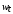 ) от уровня безработицы на 1000 чел. ( ) от уровня безработицы на 1000 чел. (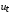 ). Статистические данные приведены в таблице: ). Статистические данные приведены в таблице:
Найдите МНК оценки регрессии 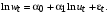 Получите 95% доверительный интервал для оценок регрессии. Проанализируйте автокорреляцию остатков. В случае наличия автокорреляции остатков выполнить ее корректировку методом Кохрейна-Оркатта. Неделя 27_2 Тема: «Модели с автокоррелированными остатками. Метод первых разностей. Устранение автокорреляции остатков методом первых разностей» Все решения заданий необходимо оформить в книге Excel. Листы книги называть номером задания. Сам файл с решениями заданий необходимо назвать фамилией студента, выполнившего задания, с пометкой учебной недели. Например, «Панов_27_2» и отправить мне на корпоративную почту в срок не позднее 15.03.2021 до 20.00 Пояснения к теме заданий. Разностный метод или метод взятия конечных разностей подразумевает переход от исходных значений временного ряда к их конечным разностям. Данный метод позволяет нивелировать влияние тенденции (зависимости временного ряда от времени) на моделируемый процесс. 1. Взятие первой разности осуществляется по формуле: 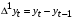 . .2. Взятие второй разности осуществляется по формуле: 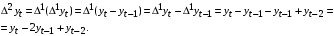 3. Аналогично можно получить формулу для конечной разности любого порядка k. 4. В частности, конечная разность третьего порядка – это первая разность от второй разности исходного временного ряда: 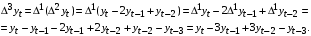 5. Для 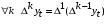 . .Задание №1. Задана зависимость 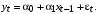 На основе данных: На основе данных:
Оценить с помощью классического МНК параметры модели регрессии. Протестировать автокорреляцию остатков. Оценить стандартные ошибки МНК параметров модели. Оценить с помощью метода первых разностей параметры модели регрессии. Определить дисперсию случайных отклонений модели в первых разностях. Оценить стандартные ошибки параметров модели в первых разностях. Сравнить полученный результат с классической моделью регрессии. Задание №2. По квартальным данным за 9 лет анализируется зависимость между экспортом ( 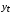 ) и импортом ( ) и импортом (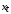 ). Статистические данные приведены в таблице: ). Статистические данные приведены в таблице:
Построить уравнение регрессии текущего импорта на текущий экспорт и константу: 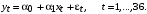 В случае наличия автокорреляции остатков выполнить ее корректировку следующими методами: а) методом первых разностей; б) при помощи лаговой зависимой переменной; в) при помощи лаговой независимой переменной. Задание №3. По динамическим данным, приведённым в таблице:
Оценить с помощью классического МНК параметры модели регрессии. Протестировать автокорреляцию остатков. Оценить стандартные ошибки МНК параметров модели. В случае наличия автокорреляции остатков выполнить ее корректировку следующими методами: а) методом первых разностей; б) при помощи лаговой зависимой переменной; в) при помощи лаговой независимой переменной. Сравнить полученный результат с классической моделью регрессии. Задание №4. Исследуется зависимость во времени количества вакансий на 1000 чел. ( 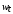 ) от уровня безработицы на 1000 чел. ( ) от уровня безработицы на 1000 чел. (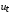 ). Статистические данные приведены в таблице: ). Статистические данные приведены в таблице:
Найдите МНК оценки регрессии 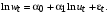 Оценить с помощью классического МНК параметры модели регрессии. Протестировать автокорреляцию остатков. В случае наличия автокорреляции остатков выполнить ее корректировку следующими методами: а) методом первых разностей; б) при помощи лаговой зависимой переменной; в) при помощи лаговой независимой переменной. Сравнить полученный результат с классической моделью регрессии. Проведите сравнительный анализ полученных моделей. Оформите результаты в виде аналитической записки. Неделя 29_1 Задания для студентов 3 курса ИЦЭиИТ по дисциплине «ЭКОНОМЕТРИКА И ЭКОНОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ», |