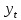Условия. Лекции по омнк на случай автокоррелированных остатков, выполните следующие задания

• Название: Лекции по омнк на случай автокоррелированных остатков, выполните следующие задания
• Дата: 31.07.2022
• Размер: 279.03 Kb.
• Имя файла: Условия.docx
• Тип: Лекции; #638485
• страница: 6 из 7

Тема: «Временные ряды. Процессы скользящего среднего q-го порядка MA(q)»

Задание №1. Вычислите автокорреляционную функцию для МА(2) процесса.

Задание №2. Покажите условия обратимости для процесса МА(2).

Задание №3. Для процесса МА(1), описанного моделью ,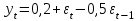

1. 
   определить математическое ожидание и дисперсию процесса, если дисперсия остатков равна 0,34;
   
2. 
   построить коррелограммы выборочной автокорреляционной функции и частной автокорреляционной функции;
   
3. 
   протестировать обратимость процесса МА(1).
   

Задание №4. Для процесса МА(1), описанного моделью ,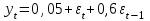

1. 
   определить математическое ожидание и дисперсию процесса, если дисперсия остатков равна 0,873;
   
2. 
   оценить коэффициенты выборочной автокорреляционной функции и частной автокорреляционной функции;
   
3. 
   протестировать обратимость процесса МА(1).
   

Задание №5. Для процесса МА(2), описанного моделью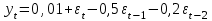

,

1. 
   определить математическое ожидание и дисперсию процесса, если дисперсия остатков равна 0,173;
   
2. 
   построить коррелограммы выборочной автокорреляционной функции и частной автокорреляционной функции;
   
3. 
   протестировать обратимость процесса МА(2).
   

Задание №6. Для процесса МА(2), описанного моделью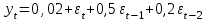

,

1. 
   определить математическое ожидание и дисперсию процесса, если дисперсия остатков равна 0,84;
   
2. 
   построить коррелограммы выборочной автокорреляционной функции и частной автокорреляционной функции;
   
3. 
   протестировать обратимость процесса МА(2).
   

Задание №7. Для процесса МА(2), описанного моделью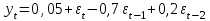

,

1. 
   определить математическое ожидание и дисперсию процесса, если дисперсия остатков равна 0,73;
   
2. 
   построить коррелограммы выборочной автокорреляционной функции и частной автокорреляционной функции.
   
3. 
   протестировать обратимость процесса МА(2).
   

Задание №8. Используя данные таблицы 1 по урожайности пшеницы в цн. на кв.км:

1. 
   Проанализируйте выборочную и частную автокорреляционные функции приведенного к стационарному виду процесса.
   
2. 
   Сделайте вывод о наличие процесса скользящего среднего определенного порядка.
   

Таблица 1 − Урожайности пшеницы в цн. на кв.км

Год	Урожайность	Год	Урожайность	Год	Урожайность
1	38	21	15	41	6
2	33	22	19	42	16
3	29	23	32	43	7
4	16	24	24	44	10
5	44	25	14	45	1
6	21	26	13	46	5
7	16	27	22	47	2
8	17	28	8	48	8
9	19	29	30	49	14
10	1	30	11	50	14
11	22	31	15	51	15
12	28	32	24	52	16
13	22	33	26	53	13
14	14	34	14	54	11
15	7	35	11	55	9
16	13	36	25	56	11
17	21	37	17	57	19
18	15	38	10	58	21
19	34	39	19
20	23	40	5

Задание №9. Используя данные таблицы 2 по урожайности ячменя в цн. на кв.км:

1. 
   Проанализируйте выборочную и частную автокорреляционные функции приведенного к стационарному виду процесса.
   
2. 
   Сделайте вывод о наличие процесса скользящего среднего определенного порядка.
   

Таблица 2 − Урожайности ячменя в цн. на кв.км

Год	Урожайность	Год	Урожайность	Год	Урожайность
1	15,2	20	15,1	39	14,0
2	16,9	21	14,6	40	14,5
3	15,3	22	16,0	41	15,4
4	14,9	23	16,8	42	15,3
5	15,7	24	16,8	43	16,0
6	15,1	25	15,5	44	16,4
7	16,7	26	17,3	45	17,2
8	16,3	27	15,5	46	17,8
9	16,5	28	15,5	47	14,4
10	13,3	29	14,2	48	15,0
11	16,5	30	15,8	49	16,0
12	15,0	31	15,7	50	16,8
13	15,9	32	14,1	51	16,9
14	15,5	33	14,8	52	16,6
15	16,9	34	14,4	53	16,2
16	16,4	35	15,6	54	14,0
17	14,9	36	13,9	55	18,1
18	14,5	37	14,7	56	17,5
19	16,6	38	14,3

Задание №10. Используя данные таблицы 3 (расстояния, пройденные британскими авиалайнерами за месяц, тыс. миль):

1. 
   Проанализируйте выборочную и частную автокорреляционные функции приведенного к стационарному виду процесса.
   
2. 
   Сделайте вывод о наличие процесса скользящего среднего определенного порядка.
   

Таблица 3 − Расстояния, пройденные британскими авиалайнерами за месяц

Год	1	2	3	4	5	6	7	8
Январь	6827	6269	8350	8186	8334	8639	9491	10840
Февраль	6178	6775	7829	7444	7899	8772	8919	10436
Март	7084	7819	8829	8484	9994	10894	11607	13589
Апрель	8162	8371	9948	9864	10078	10455	8852	13402
Май	8462	9069	10638	10252	10801	11179	12537	13103
Июнь	9644	10248	11253	12282	12950	10588	14759	14933
Июль	10466	11030	11424	11637	12222	10794	13667	14147
Август	10748	10882	11391	11577	12246	12770	13731	14057
Сентябрь	9963	10333	10665	12417	13281	13812	15110	16234
Октябрь	8194	9109	9396	9637	10366	10857	12185	12389
Ноябрь	6848	7685	7775	8094	8730	9290	10645	11595
Декабрь	7027	7602	7933	9280	9614	10925	12161	12772

Задание №11. По данным таблицы 4 о курсе акций фирмы IBM, $ США:

1. 
   Проанализируйте выборочную и частную автокорреляционные функции приведенного к стационарному виду процесса.
   
2. 
   Сделайте вывод о наличие процесса скользящего среднего определенного порядка.
   

Таблица 4 − Курс акций фирмы IBM, $ США

t		t		t
1 2 3 4 5 6 7 8 9 10	510 497 504 510 509 503 500 500 500 495	11 12 13 14 15 16 17 18 19 20	494 499 502 509 525 512 510 506 515 522	21 22 23 24 25 26 27 28 29 30	523 527 523 528 529 538 539 541 543 541

Задание №12. Используя еженедельные данные по суммарным убыткам страховой компании, y (руб.) (данные в формате Excel):

1. 
   Постройте график временного ряда, проанализируйте его структуру.
   
2. 
   Протестируйте ряд на стационарность.
   
3. 
   Если необходимо, предложите способ приведения временного ряда к стационарному виду.
   
4. 
   Проанализируйте выборочную и частную автокорреляционные функции приведенного к стационарному виду процесса.
   
5. 
   Постройте модель скользящего среднего оптимального порядка для стационарного процесса.
   
6. 
   Проверьте ограничения, накладываемые на процесс скользящего среднего.
   
7. 
   Протестируйте обратимость процесса скользящего среднего.
   
8. 
   Оформите результаты в виде аналитической записки.
   

Неделя 41