Лабораторные. Лабораторная работа 1 предполагает сбор (с сайта Росстата) и оформление в виде таблиц данных по следующим показателям

• Название: Лабораторная работа 1 предполагает сбор (с сайта Росстата) и оформление в виде таблиц данных по следующим показателям
• Дата: 01.09.2022
• Размер: 204.78 Kb.
• Имя файла: Лабораторные.docx
• Тип: Лабораторная работа; #658922
• страница: 2 из 4

Лабораторная работа 2

Построение парной линейной регрессии. Исследование зависимости выбранной зависимой переменной (Y) от независимой (Х) – от того показателя, с которым по итогам первой лабораторной работы получилась наиболее тесная связь
Количество показателей: два.

Количество наблюдений (выборка): не менее 22 (рекомендуемый исследуемый период: 1995 – 2019 гг. – если временная выборка).

1. 
   Студент строит точечную диаграмму (график).
   
2. 
   На построенном графике показывает линию тренда (линейную) и указывает величину коэффициента детерминации, а также отражает само уравнение регрессии.
   
3. 
   При помощи пакета анализа студент получает «вывод итогов», в котором акцентирует внимание на параметрах уравнения регрессии.
   
4. 
   Далее проверяет полученное уравнение регрессии на адекватность:
   

4.1. анализирует полученный коэффициент детерминации; 4.2. проверяет значимость параметров уравнения при помощи t-статистики;

4.3. проверяет значимость уравнения (коэффициента детерминации) при помощи F-статистики.
Зависимая переменная (Y) – ВРП Белгородской области

Независимая (Х) - Стоимость основных фондов (наиболее тесная связь с ВРП)

Строим точечную диаграмму (график) и на построенном графике показываем линию тренда (линейную) и указываем величину коэффициента детерминации, а также отражаем само уравнение регрессии.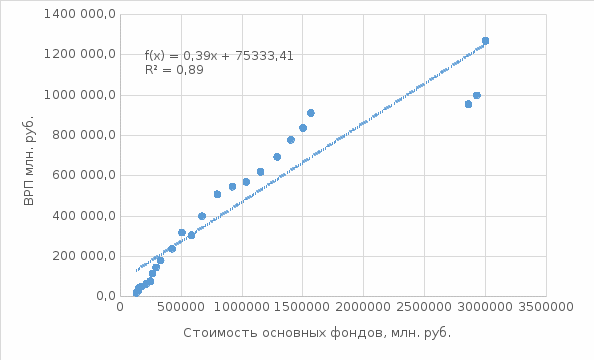

.



Рис. 1 Точечная диаграмма (график) и линия тренда

Уравнение линейной регрессии

y = 0,3917*x+75333

Величина коэффициента детерминации:

R² = r_xy² = 0,945² = 0,893

При помощи пакета анализа (инструмент Регрессия) получаем «Вывод итогов»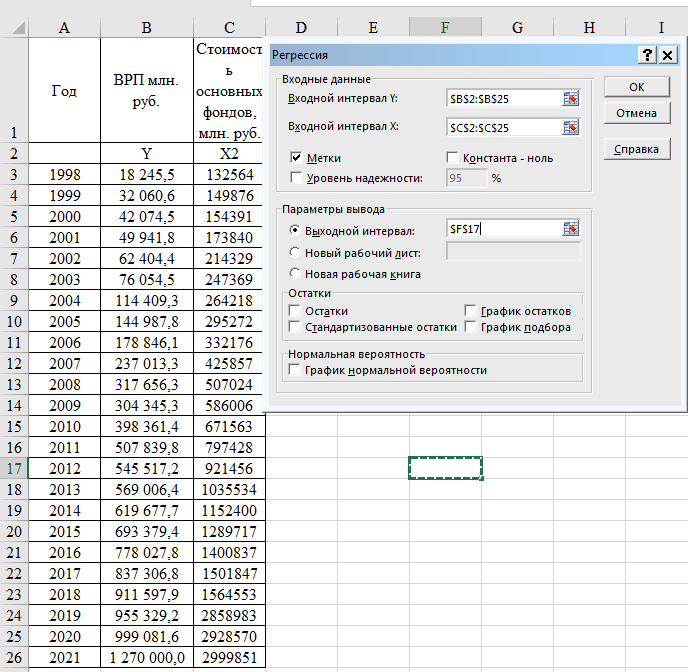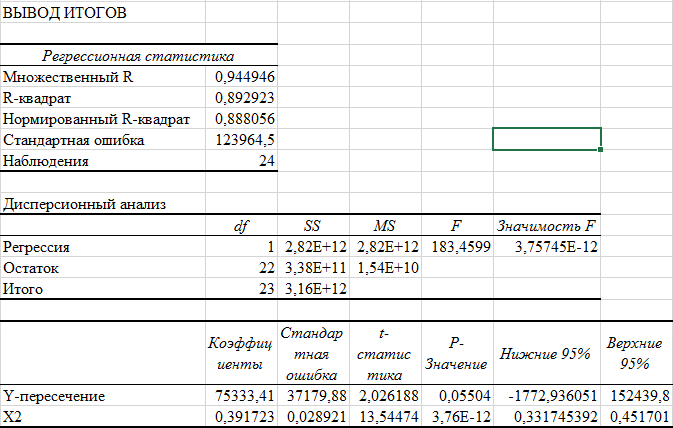



Рис. 2 Результат регрессионного анализа
Параметры уравнения регрессии y = a+bx:

a = 75333,41

b = 0,392

Уравнение регрессии (эмпирическое уравнение регрессии):

y = 0.392*x + 75333.413

Коэффициентам уравнения линейной регрессии можно придать экономический смысл.

Коэффициент регрессии b = 0.392 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 0.392.

Коэффициент a = 75333.413 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.

Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.

Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.

Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь прямая.

Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.

Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.

R²= 0.945² = 0.8929

т.е. в 89.29% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 10.71% изменения Y объясняются факторами, не учтенными в модели (а также ошибками спецификации).

Значимость параметров уравнения

Проверим гипотезу H₀ о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H₁ не равно) на уровне значимости α=0.05.

H₀: b = 0, то есть между переменными x и y отсутствует линейная взаимосвязь в генеральной совокупности;

H₁: b ≠ 0, то есть между переменными x и y есть линейная взаимосвязь в генеральной совокупности.

В случае если основная гипотеза окажется неверной, мы принимаем альтернативную. Для проверки этой гипотезы используется t-критерий Стьюдента.

Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактическим) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (которые обычно приводятся в конце учебников и практикумов по статистике или эконометрике).

Табличное значение определяется в зависимости от уровня значимости (α) и числа степеней свободы, которое в случае линейной парной регрессии равно (n-2), n-число наблюдений.

Если фактическое значение t-критерия больше табличного (по модулю), то основную гипотезу отвергают и считают, что с вероятностью (1-α) параметр или статистическая характеристика в генеральной совокупности значимо отличается от нуля.

Если фактическое значение t-критерия меньше табличного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр или статистическая характеристика в генеральной совокупности незначимо отличается от нуля при уровне значимости α.

t_крит(n-m-1;α) = t_крит(22;0.05) = =СТЬЮДЕНТ.ОБР.2Х(0,05;22) = 2.074
S_b - стандартное отклонение случайной величины b (это столбец стандартное отклонение).

На рис. 2 t_b = 13,54 - это столбец t-статистика

Поскольку 13.54 > 2.074, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
S_a - стандартное отклонение случайной величины a (это столбец стандартное отклонение).

На рис. 2 t_a = 2,026 - это столбец t-статистика

Поскольку 2.026 < 2.074, то статистическая значимость коэффициента регрессии a не подтверждается (принимаем гипотезу о равенстве нулю этого коэффициента). Это означает, что в данном случае коэффициентом a можно пренебречь.

F-статистика. Критерий Фишера.

Коэффициент детерминации R² используется для проверки существенности уравнения линейной регрессии в целом.

Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.

Если расчетное значение с k₁=(m) и k₂=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

Выдвигаем нулевую гипотезу о том, что уравнение в целом статистически незначимо: H₀: R²=0 на уровне значимости α.

Определяют фактическое значение F-критерия:
n = 24; m = 1

Fфакт = 183,46 – столбец F на рис. 2

Табличное значение

F_табл = =FРАСПОБР(0,05;1;22) = 4,3

Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.

В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.

Поскольку фактическое значение F > F_табл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).
Выводы.

Изучена зависимость Y от X. На этапе спецификации была выбрана парная линейная регрессия. Оценены её параметры. Статистическая значимость уравнения проверена с помощью коэффициента детерминации и критерия Фишера. Установлено, что в исследуемой ситуации 89.29% общей вариабельности Y (ВРП) объясняется изменением X (Стоимость основных фондов). Установлено также, что параметры модели статистически не значимы. Возможна экономическая интерпретация параметров модели - увеличение X (Стоимость основных фондов) на 1 млн. руб. приводит к увеличению Y (ВРП) в среднем на 0.392 млн. руб.