Макросы. Лабораторные работы в Excel. Лабораторная работа 1. Презентация с использованием PowerPoint
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
Таблица 6.2 – Результаты вычислений амортизационных отчислений
Выводы: изучена встроенная функция ДДОБ, с помощью которой можно вычислить величину амортизационных отчислений. Лабораторная работа №7. Информационные технологии решения задач бизнес-анализа Цель работы: Научиться находить оптимальное решение в условиях дефицита ресурсов с использованием компьютерной технологии. Постановка задачи: Фирма выпускает продукцию 4 видов: продукт 1, продукт 2, продукт 3 и продукт 4. Для выпуска использует 3 вида ресурсов: трудовые, сырьевые, финансовые. Известны: нормы расходов (количество ресурса каждого вида), необходимые для выпуска единицы продукции данного типа, сколько ресурса имеется в наличии, а также прибыль, получаемая от реализации единицы каждого типа продукции – см. таблицу 7.1. Определить, в каком количестве нужно выпускать продукцию каждого вида, чтобы получить от ее производства максимальную прибыль. Таблица 7.1 – Исходные данные
Ход выполнения работы: Введем обозначения, пусть xj – количество выпускаемой продукции j-го вида, j = 1, 2, 3, 4; Bi – количество имеющегося в наличии ресурса i-го вида, i = 1, 2, 3; Aij – норма расхода ресурса i-го вида для производства единицы продукции j-го вида; Cj – прибыль, получаемая от реализации единицы продукции j-го вида. Тогда требуется решить следующую задачу оптимизации: F = 60x1 + 70x2 + 120x3 + 130x4 -> max x1 + x2 + x3 + x4 ≤ 16 6x1 + 5x2 + 4x3 + 3x4 ≤ 110 4x1 + 6x2 + 10x3 + 13x4 ≤100. На рабочем листе Excel подготовим форму для ввода условий задачи. Для этого в ячейку D1 введем слово Переменные , а в ячейку D7 – Ограничения. Далее в диапазон B2:E3 ввести соответственно Продукция1, …, Продукция 4. В ячейку A2 – Имя, А3 – Значение, А4 – Нижняя граница, А5 – Верхняя граница, А6 – Коэффициенты целевой функции и т.д. Все это является комментариями и на решение задачи никак не повлияет. Далее производим заполнение таблицы исходными данными согласно данным таблицы 7.1. Заполненная форма представлена на рис. ниже. 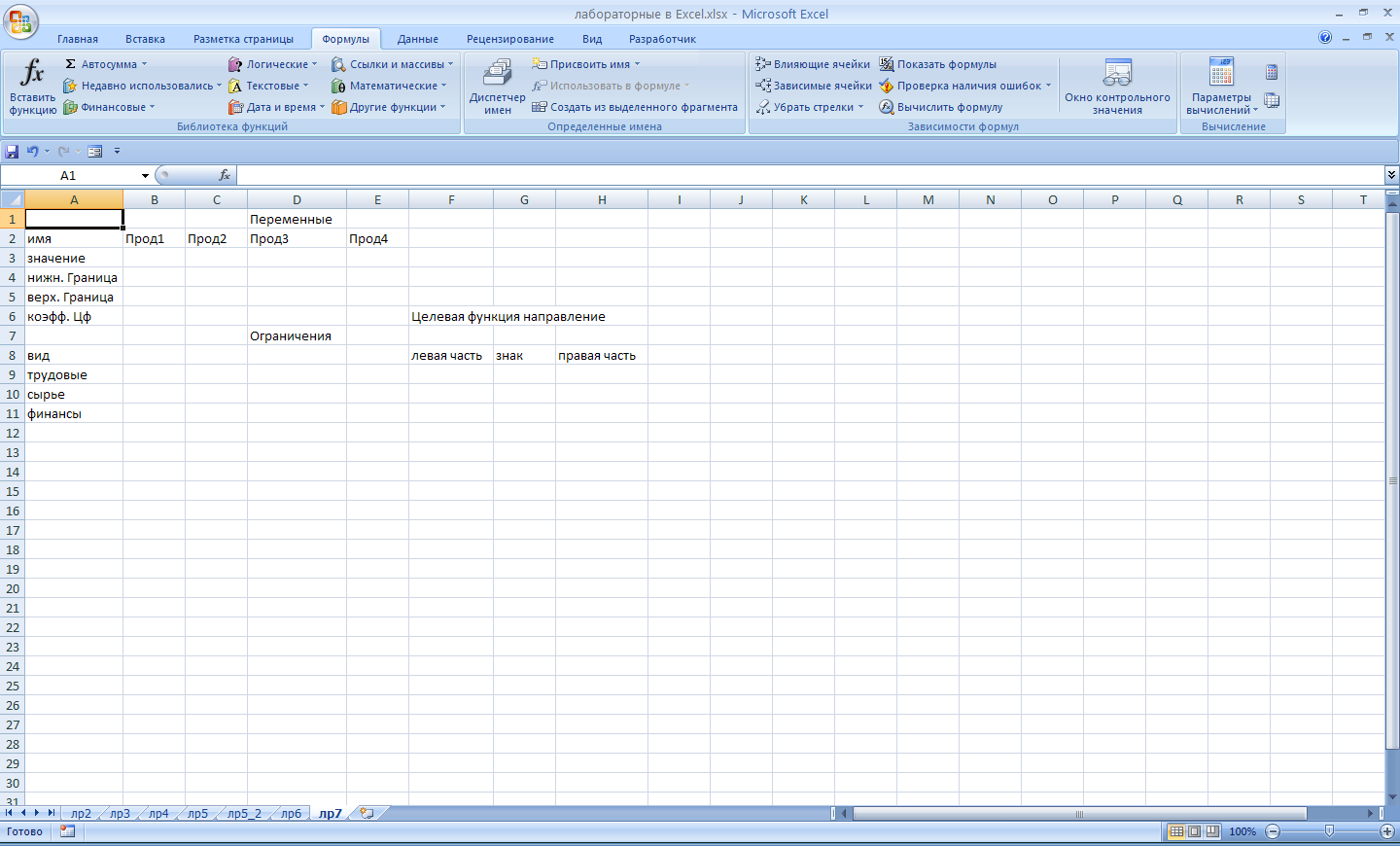 Введем зависимости для целевой функции и левой части ограничений. Так в ячейку F6 (значение целевой функции) введем следующую формулу =СУММПРОИЗВ(B3:E3;B6:E6). А в ячейку F9 введем формулу =СУММПРОИЗВ($B$3:$E$3;B9:E9). Протянем эту функцию на ячейки F10:F11. В итоге мы заполнили таблицу исходными данными и вычислимыми полями. Можно переходить к нахождению оптимального решения – см. рис. ниже. 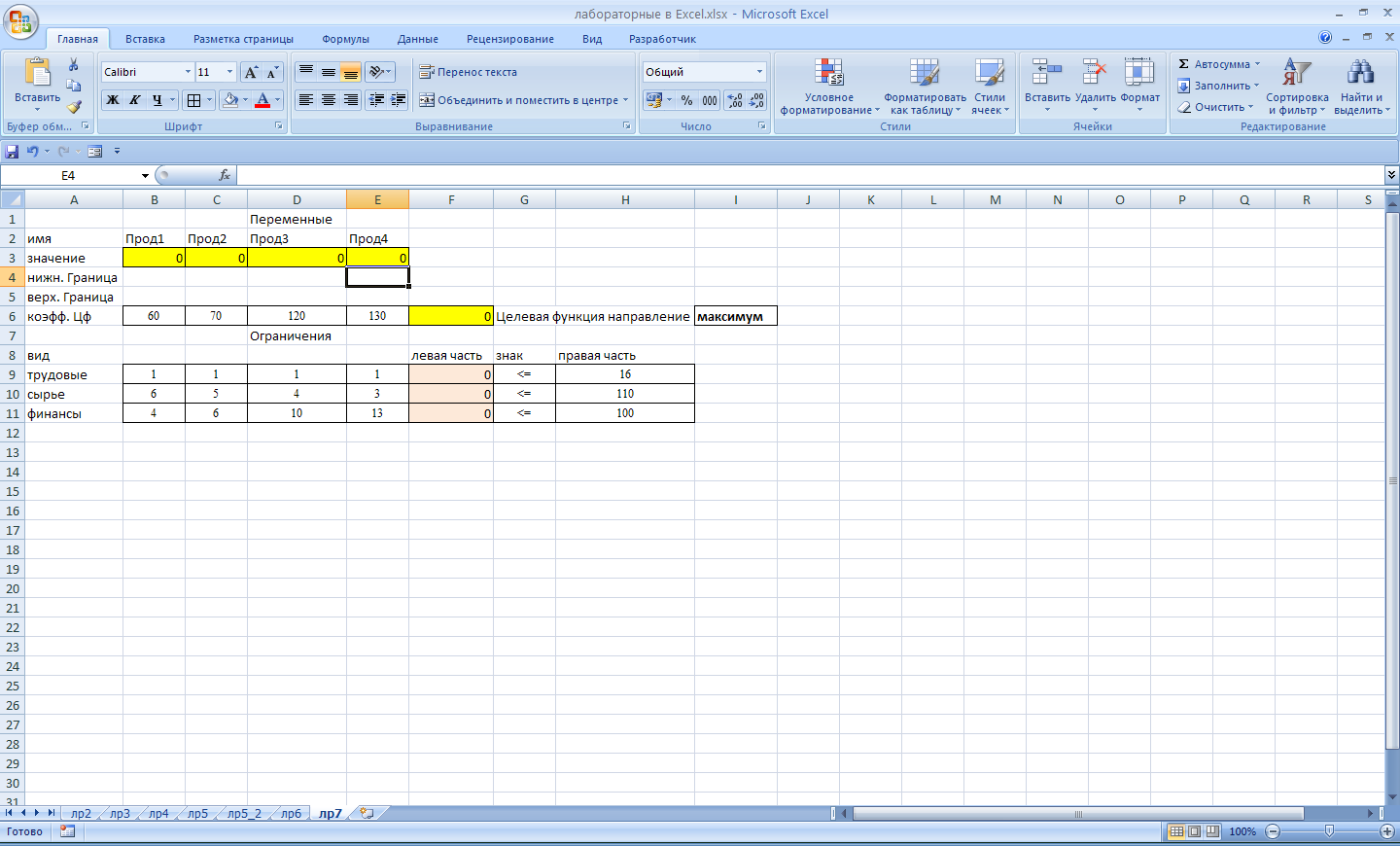 Воспользуемся функционалом Поиск решения. Установим следующие параметры. 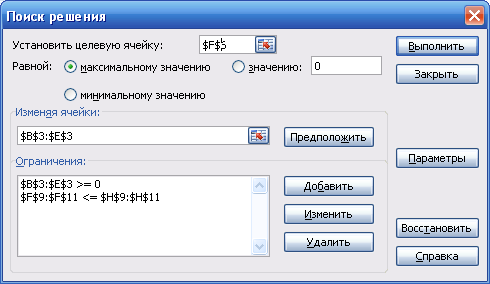 Нам будет выдано следующее диалоговое окно:  Решение найдено, после нажатия кнопки Ok, мы увидим его в нашей таблице. Так нам следует производить продукт 1 в количестве 10 штук, продукт 3 в количестве 6 штук и не производить продукты 2 и 4 вовсе. При этом прибыль составит 1320 ден. ед. – см. ниже. При этом количество использованных трудовых ресурсов составит 16, сырьевых 84, а финансовых – 100. То есть финансы и трудовые ресурсы были использованы в полном объеме, а сырье – нет (остаток составляет 16 ед.). 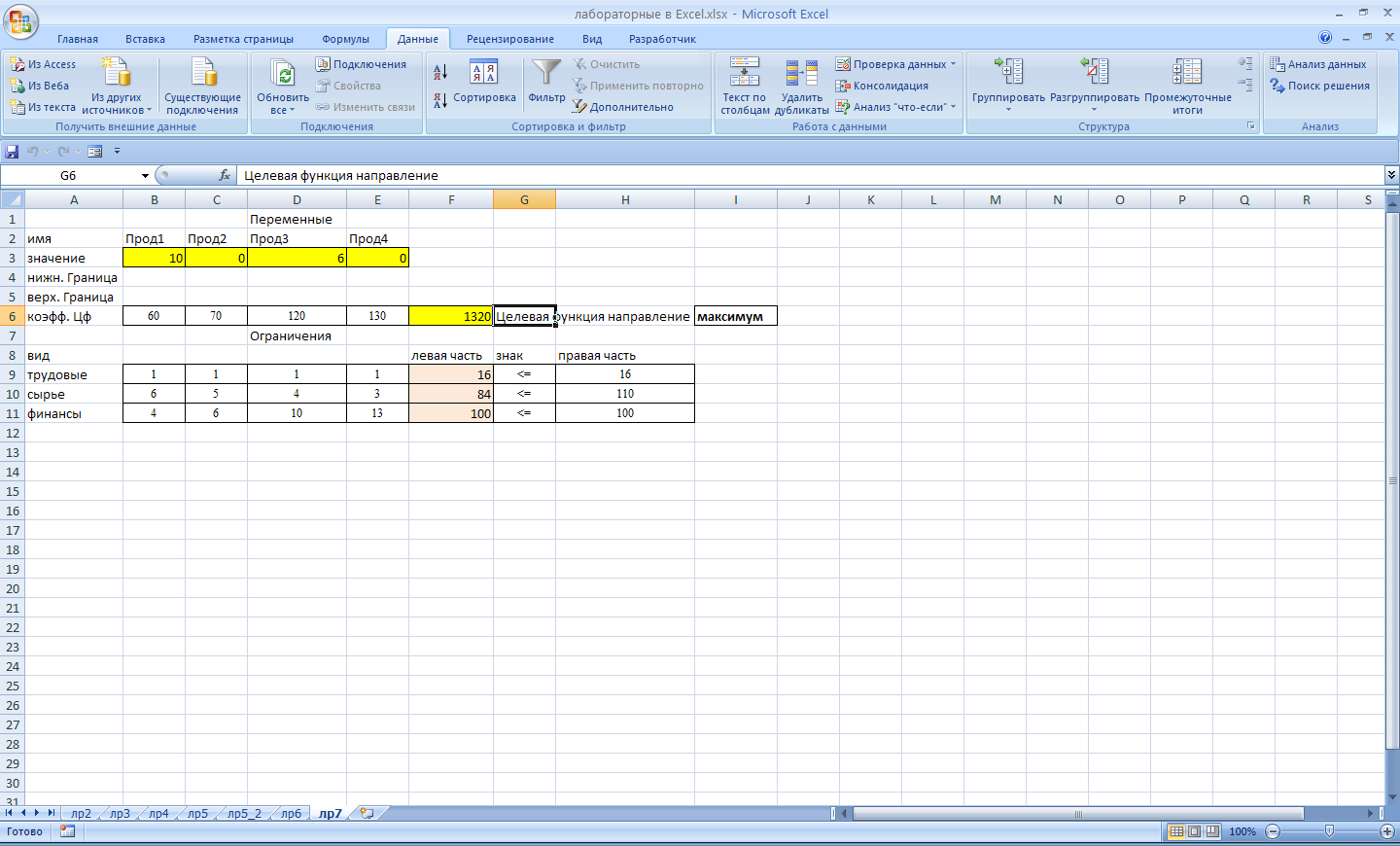 Дополнительно посмотрим результаты нахождения решения. Повторно вызовем диалоговое окно Поиск решения, не изменяя параметров поиска выберем пункт Результаты, в результате получим следующую таблицу.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
