лабораторная матлаб. Лабораторная работа 1. Лабораторная работа 1 применение методов вычислительной математики в задачах обработки экспериментальных данных вариант 7 Содержание

• Название: Лабораторная работа 1 применение методов вычислительной математики в задачах обработки экспериментальных данных вариант 7 Содержание
• Анкор: лабораторная матлаб
• Дата: 26.02.2023
• Размер: 273.43 Kb.
• Имя файла: Лабораторная работа 1.docx
• Тип: Лабораторная работа; #956193

Лабораторная работа № 1

ПРИМЕНЕНИЕ МЕТОДОВ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ В ЗАДАЧАХ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Вариант № 7

Содержание

Индивидуальное задание 3

Задание 1. 3

Задание 2. 4

Выполнение работы 5

Задание 1. 5

Задание 2. 12

Индивидуальное задание

Задание 1.

Дать геометрическое представление табулированной функции. Двумерную геометрическую реализацию обеспечить следующими функциями: plot, bar, line, stem.

Применяя методы интерполяции решить прикладную задачу, соответствующую варианту задания. Использовать полиномиальную интерполяцию и встроенные функции пакета Matlab с различными способами кусочно-непрерывной интерполяции (по соседним элементам, линейную интерполяцию, кубическими сплайнами, кубическими эрмитовыми сплайнами),

Исходя из эмпирического анализа данных и сравнительного анализа результатов всех видов интерполяции, сделать выводы.

Найти и графически отобразить графики первой и второй производных по аргументу (), использовав встроенные возможности пакета.

Используя интерполяционных подход и встроенные функции пакета Matlab, вычислить и графически отобразить функциональную зависимость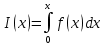



Дана зависимость значений электродвижущей силы Е от температуры, найти значение э.д.с. при значении температуры 950С:

Задание 2.

Используя возможности интерполирования многомерных данных дать графическую интерпретацию результатам, представленным в задании.

Координаты сетки определить исходя из размера единичных отрезков абсциссы и ординаты графика.

Экспериментальные данные распределения температуры (в усл.ед.) в некоторый момент времени на поверхности трубы представлены на рисунке.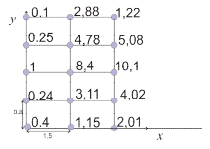

Выполнение работы

Задание 1.

Дать геометрическое представление табулированной функции. Двумерную геометрическую реализацию обеспечить следующими функциями: plot, bar, line, stem.

Зададим функцию двумя векторами – T и E.

T=[0 200 400 600 800 1000 1200 1400 1600]';

E=[0 1.44 2.26 5.24 7.34 9.61 11.96 14.36 16.73]';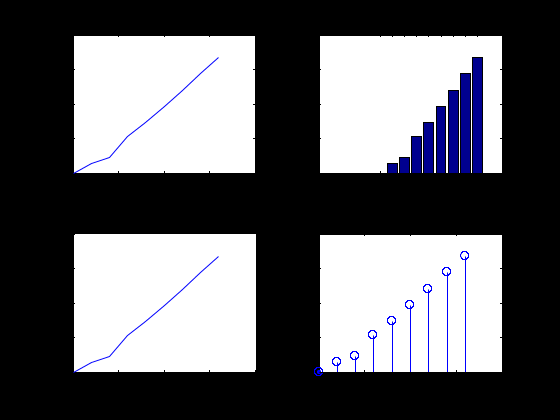



Применяя методы интерполяции решить прикладную задачу, соответствующую варианту задания. Использовать полиномиальную интерполяцию и встроенные функции пакета Matlab с различными способами кусочно-непрерывной интерполяции (по соседним элементам, линейную интерполяцию, кубическими сплайнами, кубическими эрмитовыми сплайнами),

Создадим функцию, возвращающую значение многочлена

function z=Lagr(x,i,X,Y)

N=length(X);

L=1;

for j=1:N

if not(j==i)

L=L*(x-X(j))/(X(i)-X(j));

end;

end;

z=L*Y(i);

end

Создадим файл Pol_Lagr.m, возвращающий значение полинома Лагранжа

function z=Pol_Lagr(x,X,Y)

N=length(X);

s=0;

for i=1:N

s=s+Lagr(x,i,X,Y);

end;

z=s;

end

Значения табличной функции и интерполированные значения функции

представлены на графике.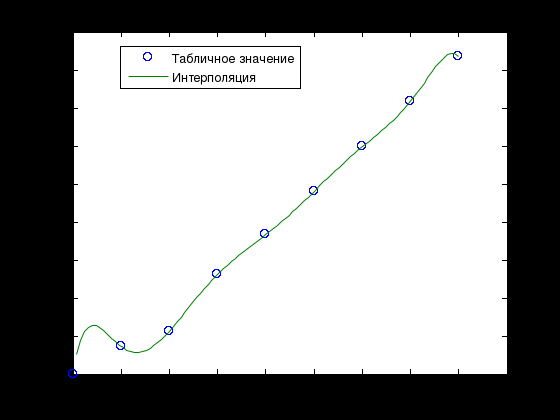



Используем встроенные функции пакета Matlab с различными способами кусочно-непрерывной интерполяции.

Линейная интерполяция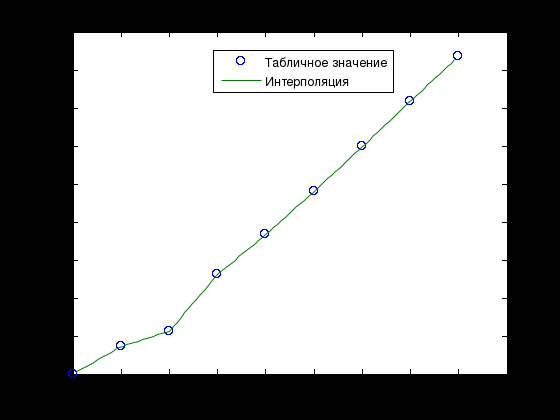



Интерполяция кубическими сплайнами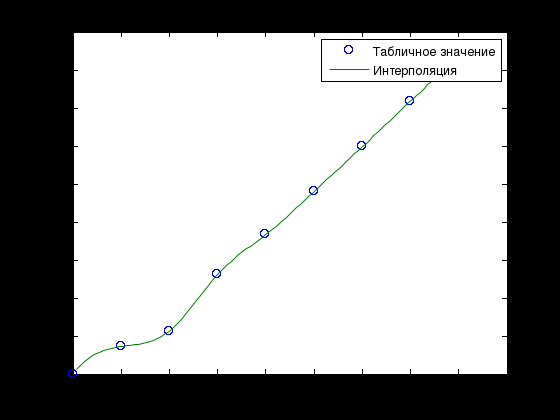



Интерполяция по соседним элементам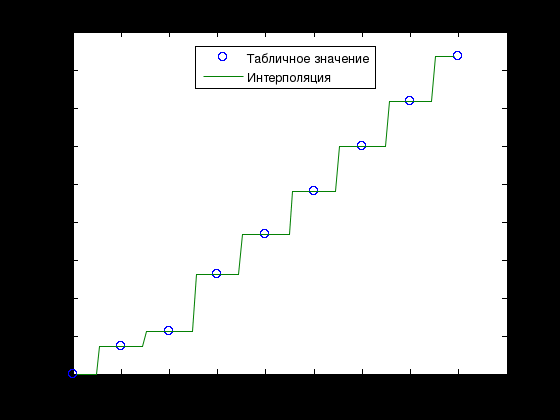



Интерполяция кубическими эрмитовыми сплайнами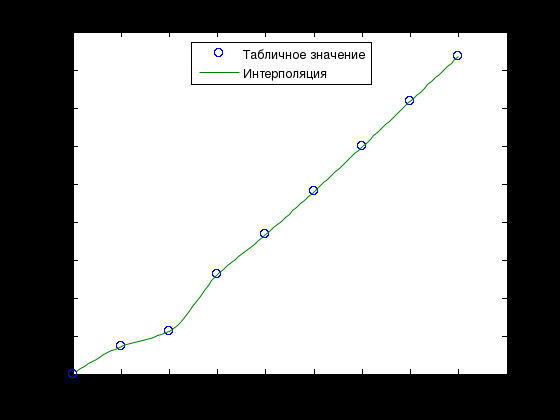



Найдем значение э.д.с. при значении температуры 950С с помощью различных методов интерполяции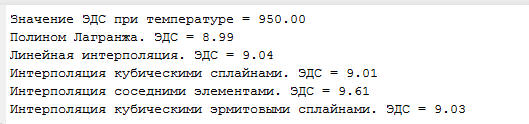



Исходя из графиков и полученных значений видим, что наиболее точно интерполировано с помощью кубических сплайнов и эрмитовых кубических сплайнов.

Найти и графически отобразить графики первой и второй производных по аргументу (), использовав встроенные возможности пакета.

Листинг программы, численно дифференцирующей аналитически заданную функцию, представлен ниже. Используем интерполяцию сплайнами.

%Первая производная

D1E=diff(E)/h;

%Вторая производная

D2E=diff(D1E)/h;

N=length(T);

i=1:N-1;

j=1:N-2;

D1ESpl=spline(T(i),D1E(i),t);

D2ESpl=spline(T(j),D2E(j),t);

figure

plot(t,D1ESpl,t,D2ESpl)

xlabel('\itT') % метка оси x

ylabel('\itE\rm(\itT\rm)') % метка оси y

title('Производные');

legend('Первая производная','Вторая производная');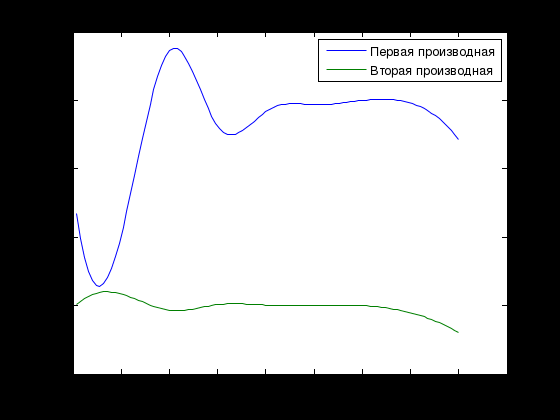



Используя интерполяционных подход и встроенные функции пакета Matlab, вычислить и графически отобразить функциональную зависимость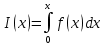



%Вычислим интеграл в точках

for i=2:length(t)

T1=t(1:i);

E1=E_Spl(1:i);

I(i)=trapz(T1,E1);

end;

figure

plot(t,I)

xlabel('\itT') % метка оси x

ylabel('\itI\rm(\itT\rm)') % метка оси y

title('Зависимость I(x)');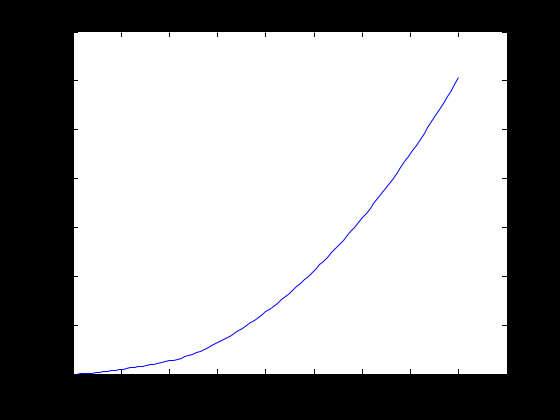

Задание 2.

Используя возможности интерполирования многомерных данных дать графическую интерпретацию результатам, представленным в задании.

Координаты сетки определить исходя из размера единичных отрезков абсциссы и ординаты графика.

Экспериментальные данные распределения температуры (в усл.ед.) в некоторый момент времени на поверхности трубы представлены на рисунке.



clc;

clear all

close all

x=[0 1.5 3]';

y=[0 0.8 1.6 2.4 3.2]';

z=[0.4 1.15 2.01;

0.24 3.11 4.02;

1 8.4 10.1;

0.25 4.78 5.08;

0.1 2.88 1.22];

[Xi,Yi]=meshgrid(0:0.1:4);

ZBiLNear=interp2(x,y,z,Xi,Yi,'nearest');

ZBiLin=interp2(x,y,z,Xi,Yi,'bilinear');

ZBiCub=interp2(x,y,z,Xi,Yi,'bicubic');

subplot(2,2,1)

surf(x,y,z)

title('Табличная функция');

subplot(2,2,2)

surf(Xi,Yi,ZBiLNear)

title('Интерполяция соседними элементами');

subplot(2,2,3)

surf(Xi,Yi,ZBiLin)

title('Билинейная интерполяция');

subplot(2,2,4)

surf(Xi,Yi,ZBiCub)

title('Кубическая интерполяция');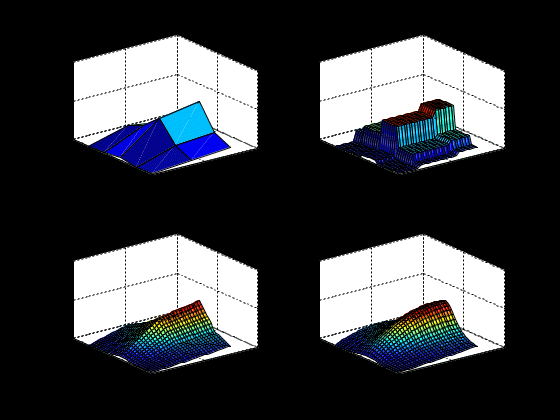