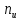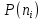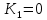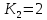ПОНИС. Лабораторная работа 1 Расчет и исследование показателей надежности необслуживаемых и обслуживаемых ис
 Скачать 44.88 Kb. Скачать 44.88 Kb.
|
Лабораторная работа №1 Расчет и исследование показателей надежности необслуживаемых и обслуживаемых ИСЦель работы: исследование и получение практических навыков оценки показателей надежности ИС Основные теоретические положения Невосстанавливаемые объекты могут иметь только один отказ. Эти объекты в процессе выполнения своих функций не допускают ремонта, и если происходит отказ такого объекта, то выполняемая операция считается не выполненной. Показатели надежности используются как для оценки надежности невосстанавливаемых ИС, так и для восстанавливаемых ИС. Вероятность безотказной работы P(t) - вероятность того, что в пределах заданной наработки отказ объекта не возникнет. То есть, конкретное численное значение вероятности безотказной работы имеет смысл лишь тогда, когда оно поставлено в соответствие заданной наработке, в течение которой возможно возникновение отказа. Как правило, вероятность безотказной работы определяется в предположении, что в начальный момент времени исчисления заданной наработки ИС была работоспособна. Кроме понятия «вероятность безотказной работы», достаточно часто используют вспомогательные показатели: вероятность отказа Q(t) и ее производная по времени φ(t)- плотность распределения наработки до отказа. Под вероятностью отказа понимают вероятность того, что система откажет хотя бы один раз в течение заданного времени работы t0, будучи работоспособным в начальный момент времени. φ(t) характеризует скорость снижения надёжности ИС во времени. Средняя наработка до отказа – это математическое ожидание исправной работы ИС до отказа. Гамма-процентная наработка на отказ – это наработка, в течение которой отказ изделия не возникнет с вероятностью γ, выраженной в процентах, то есть Pγ = γ/100 Интенсивность отказов – это условная плотность вероятности отказа ИС на некоторый момент времени наработки при условии, что до этого момента отказов не было. Задание 1 При проектировании информационной системы следует обеспечить надежность безотказной работы системы в длительном режиме функционирования P(t)≥ 0,97. Исходные данные: 1. Проектируемая система состоит из n элементов. 2. Средняя интенсивность отказов для элементов системы – λ. 3. Время, для которого определяется вероятность безотказной работы ИС – t. 4. Вероятность безотказной работы системы подчиняется экспоненциальному закону распределения, система невосстанавливаемая. Таблица 1
Вероятность безотказной работы проектируемой системы (если не принимать дополнительных мер) составляет: 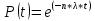 Вычислим P(t) учетом исходных данных 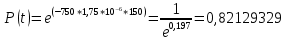 Полученное значение вероятности безотказной работы ИС не удовлетворяет поставленным требованиям P(250)≥0,97. Рассмотрим возможные способы повышения надежности проектируемой системы. Для этого определим условия, при которых 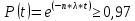 Решив последнее уравнение относительно параметров n, λ, t, получим 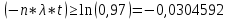 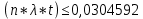 Обеспечить выполнение заданного требования по значению надежности ИС возможно, если n, при прочих равных условиях будет принимать следующие значения: 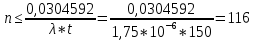 Результаты расчетов показывают, что для удовлетворения требований по значению вероятности безотказной работы ИС необходимо сократить количество элементов с 750 до 116 Обеспечить выполнение требования по значению надежности ИС возможно, если повысить надежность входящих в систему элементов, при прочих равных условиях, до следующих значений: 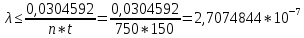 То есть, для удовлетворения требований по значению вероятности безотказной работы ИС необходимо повысить надежность входящих в состав системы элементов (уменьшить интенсивность отказов) практически в шесть раз. Обеспечить выполнение требования по значению надежности ИС возможно, если уменьшить время работы системы, при прочих равных условиях, до следующих значений: 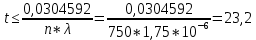 Как показывают результаты вычислений, обеспечить выполнение требования по значению надежности ИС возможно, если уменьшить время работы системы до величины 23 часов. Лабораторная работа №2 Расчет и исследование показателей надежности программных средств ИСЦель работы: освоить особенности расчета основных показателей надежности ПО информационных систем. Надежность современных информационных систем определяется не только безотказной работой технических средств, но и надежностью программного обеспечения (программных средств). Под надежностью программных средств обычно понимают совокупность свойств, характеризующих их способность сохранять заданный уровень пригодности в заданных условиях в течение заданного интервала времени. Модели надежности программ строятся на предположении о том, что проявление ошибки является случайным событием и поэтому имеет вероятностный характер. Такие модели предназначены для оценки показателей надежности программ и программных комплексов в процессе тестирования. Модель Миллса предусматривает внесение в исследуемую программу перед началом тестирования некоторого количества случайных (искусственных) ошибок. Тестирующей группе неизвестно ни количество, ни характер вносимых ошибок. Предполагается, что все ошибки (внесенные и ранее существующие собственные ошибки) программы имеют равную вероятность быть обнаруженными в процессе тестирования. Задача 2 При расчетах использовать модель надежности программного обеспечения Миллса, параметрами которой являются: Eu – количество искусственно внесенных в программу ошибок; nu – количество обнаруженных искусственных внесенных ошибок. При решении задачи следует определить: 1. Значение вероятности присутствия в тестируемой программе Ki ошибок. 2. Построить графики зависимости значений вероятности присутствия в программе Ki ошибок от значений nu при заданных значениях Nu. Диапазон изменения nu – от 1 до Nu, с шагом изменения – 1. Таблица 2
В случаях, когда в процессе тестирования выявляется nи внесенных ошибок, для расчета вероятности наличия в тестируемой программе K ошибок используется следующее выражение: 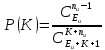 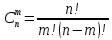 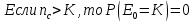 Вычисляем величину вероятности того, что программа не имеет ни одной собственной ошибки. При 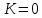 Для 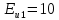 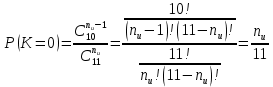 Для 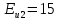 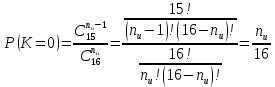 Для 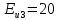 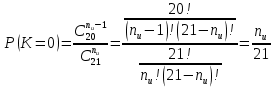 При 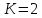 Для 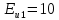 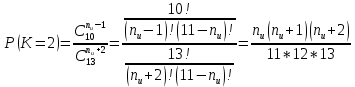 Для 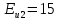 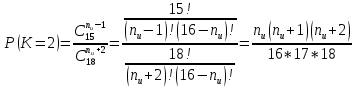 Для 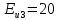 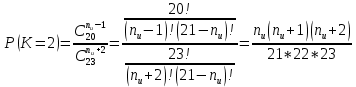 Для построения требуемых графиков с использованием программы Exsel следует сформировать таблицы значений параметров надежности программного обеспечения ИС. Значения вероятности содержания в тестируемой программе Ki ошибок при различных значениях 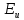 Таблица 3
Таблица 4
Таблица 5
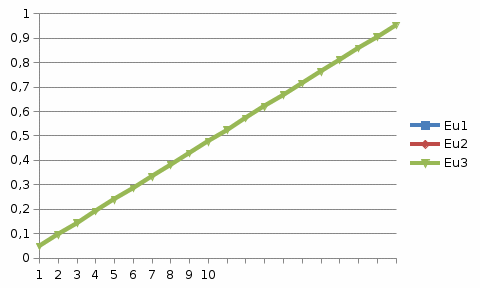 Рисунок 1 График значений вероятности отсутствия в тестируемой программе собственных ошибок 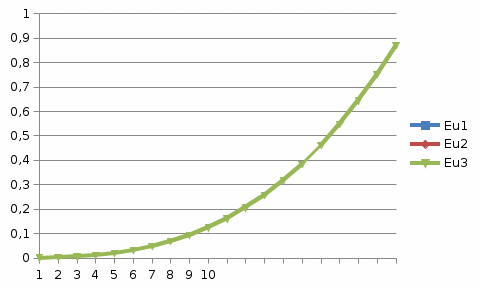 Рисунок 2 График значений вероятности присутствия в тестируемой программе трех собственных ошибок Лабораторная работа №3 Исследование методов повышения надежности ИСПри проектировании информационной системы обеспечить надежность безотказной работы системы в длительном режиме функционирования P(t)≥ 0,97. Для решения задачи использовать метод резервирования всей системы. Исходные данные: 1. Проектируемая система состоит из n элементов. 2. Средняя интенсивность отказов для элементов системы – λ. 3. Время, для которого определяется вероятность безотказной работы ИС – t. 4. Вероятность безотказной работы системы подчиняется экспоненциальному закону распределения, система невосстанавливаемая. При решении задачи следует определить: 1. Кратность резервирования всей системы (m), обеспечивающую требуемое значение вероятности безотказной работы - P(t). 2. Построить графики зависимости надежности ИС от времени при различных значениях m. Диапазон изменения времени функционирования – от 0 до 400, с шагом изменения – 25. Значения m выбрать равными 0,1, 2, 3. Таблица 6
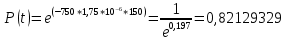 Полученное значение вероятности безотказной работы ИС не удовлетворяет поставленным требованиям P(150)≥0,97. Используем способ повышения надежности проектируемой системы предусматривающий резервирование всей системы с постоянно подключенным резервом. В этом случае, параллельно основной системе подключаются резервные ИС, надежность такой схемы определяется выражением. 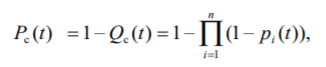 Где n=m+1, m – искомое значение кратности резервирования системы, а pi = P(150) для всех i =1,2, …, n. В этом случае последнее выражение можно представить в следующем виде. 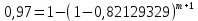 Откуда искомое значение кратности резервирования системы определится как: 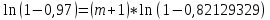 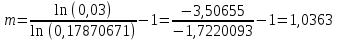 Таким образом, для обеспечения заданного значения вероятности безотказной работы ИС для t=250 ч достаточно однократного резервирования всей системы, то есть m=1. Для проверки полученного результата рассчитаем вероятность безотказной работы системы для полученного варианта резервирования. При однократном резервировании 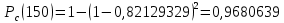 Таблица 7
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||