лаборотрная работа. 10_лабораторная_работа_Скорость_звука. Лабораторная работа 10 Определение скорости звука в воздухе (газах) Цель работы
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
Лабораторная работа №10 Определение скорости звука в воздухе (газах) Цель работы: Определение фазовой скорости распространения звуковой волны в воздухе, методом измерения времени распространения звуковых импульсов в трубке Кундта. Необходимые приборы и принадлежности: Трубка Кундта модели Е - U8498308 для измерения времени распространения звуковых импульсов. Блок формирования звуковых импульсов модели К - U8498281. Длинный акустический зонд - U8498282. Короткий акустический зонд - U8498307. Блок усилителя для акустических зондов: (230 В, 50/60 Гц) - U8498283-230 или (115 В, 50/60 Гц) - U8498283-115. Микросекундный счетчик: (230 B, 50/60 Гц) - U8498285-230 или (115B, 50/60 Гц) - U8498285-115. Нагревательный стержень модели К - U8498280. Высокочастотный соединительный шнур, байонетный разъём/4-мм штекер (2шт) - U11257. Источник питания постоянного тока с напряжением 0 – 20 В, 0 – 5 А (230 В, 50/60 Гц) – U33020-230 или 0 – 20 В, 0 – 5 А (115 В, 50/60 Гц) – U33020-115. Цифровой быстродействующий карманный термометр - U11853. Никель-хром-никелевый погружной датчик типа К с диапазоном измерения от -65 0С до 550 0С - U11854. Пара безопасных соединительных проводов для опытов длиной 75 см - U13812. Дополнительно рекомендуется иметь: различные технические газы. Для допуска к работе студенты должны знать следующие вопросы: Что такое волна, волновой фронт, волновая поверхность? Основное свойство волны. Чем продольная волна отличается от поперечной? Написать уравнение бегущей волны и разъяснить смысл входящих в него величин. По какой траектории движется частица в бегущей продольной волне? Что называется, звуком и высотой звука? От чего зависит громкость звука? Чем определяется скорость звука в воздухе? С какой скоростью звук распространяется в газе, жидкости, твердом теле? Что такое фазовая и групповая скорости волны? В чём отличие фазовой скорости волны от групповой? Краткие сведения из теории вопроса (теоретическое введение): Из курса физики известно, что колеблющееся тело (струна, камертон, диффузор динамика), находящееся в упругой среде, приводит в колебательное движение частицы этой среды соприкасающиеся с ним. Атомы и молекулы среды, прилегающие к этому телу периодический подвержены сгущению и разрежению, т.е. растяжению или сжатию среды, что в свою очередь, ведет к возникновению упругих сил, которые стремятся вернуть элементы (атомы или молекулы) среды в первоначальное состояние равновесия. Так как соседние элементы среды взаимодействуют друг с другом, то эти упругие деформации будут передаваться от одних участков среды к другим. Процесс распространения колебательного движения в среде называется волновым процессом или просто распространением волны. Если в распространении волны участвуют частицы среды, то такие волны называют механическими волнами. Механические волны могут быть продольными, когда частицы среды колеблются вдоль линии, совпадающей с направлением распространения колебания, а также могут быть и поперечными, когда частицы колеблются перпендикулярно к направлению распространения волны. Продольные волны возникают в таких средах, где могут возникать деформации растяжения или сжатия: то есть в твердых телах, жидкостях и газах. Поперечные волны распространяются там, где возможны деформации сдвига: то есть только в твердых телах. Таким образом, в твердых телах могут распространяться как продольные, так и поперечные волны, причем скорости их распространения разные. Поверхность, до которой доходит колебание в некоторый момент времени, называется фронтом волны. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт в каждый момент времени только один. Волновые поверхности остаются неподвижными. Волновой фронт все время перемещается. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической волне – множество концентрических сфер. Рассмотрим частицу упругой среды, находящуюся в точке 0 и совершающего колебательное движение по закону: 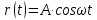 , (1) , (1)где 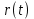 – смещение частицы среды от положения равновесия; A– амплитуда (наибольшее смещение частицы среды от положения равновесия); 𝑡 – время; 𝜔=2𝜋/𝑇 – циклическая или круговая частота; 𝑇 – период (время одного полного колебания); то в некоторую произвольную точку С среды придет колебательное движение с некоторым запаздыванием на время 𝜏=𝑥/𝑢, где 𝑥 − расстояние, на которое распространилось колебание от точки 0 до С, 𝑢− скорость распространения волны (фазовая скорость волны). – смещение частицы среды от положения равновесия; A– амплитуда (наибольшее смещение частицы среды от положения равновесия); 𝑡 – время; 𝜔=2𝜋/𝑇 – циклическая или круговая частота; 𝑇 – период (время одного полного колебания); то в некоторую произвольную точку С среды придет колебательное движение с некоторым запаздыванием на время 𝜏=𝑥/𝑢, где 𝑥 − расстояние, на которое распространилось колебание от точки 0 до С, 𝑢− скорость распространения волны (фазовая скорость волны). Уравнение зависимости смещения частицы среды от времени в точке Сзапишется как: 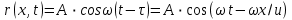 , (2) , (2)где 𝜔/𝑢 = 2𝜋/(𝑇⋅ 𝑢) = 2𝜋/𝜆 = 𝑘 – волновое число; 𝜆 = 𝑇⋅ 𝑢 −длина волны. Таким образом, волна, распространяющаяся в направлении 0С в бесконечном упругом стержне или протяженном столбе газа (воздуха), описывается уравнением плоской монохроматической бегущей волны: 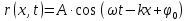 , (3) , (3)где 𝜑 = (𝜔𝑡 − 𝑘𝑥 + 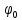 ) – фаза волны, а ) – фаза волны, а 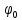 – начальная фаза. – начальная фаза. Уравнение волны (3), а также волны более сложного вида являются решением одномерного волнового уравнения: 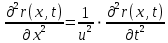 , (4) , (4)где 𝑢 –фазовая скорость, связанная с 𝜔 и 𝑘 соотношением: 𝑢 = 𝜔/𝑘 = 𝜆/𝑇 = 𝜆⋅𝜈, где в свою очередь, 𝜈− линейная частота колебаний. Фазовая скорость u – это скорость движения определенного значения фазы, однозначно характеризующего фиксированное состояние колебательного движения частиц среды. Расстояние 𝜆, пройденное волной (определенной фазой колебания) за один период колебания, называется длиной волны, т.е. длина волны – кратчайшее расстояние между соседними частицами среды, колеблющимися в одинаковой фазе. Частоты колебаний 𝜈 частиц среды имеют ту же частоту, что и частота колебаний источника волн. Волны, частоты колебаний частиц которых лежат в пределах от 16 до 20000 Гц, называются звуковыми. Звуковые волны в газах и жидкостях являются продольными и могут распространяться только в упругой среде. Рассмотрим распространение продольной волны в газе (воздухе). Молекулы газа движутся хаотически, но в силу того, что при образовании волны возникают области сжатия и разрежения, то в этих местах происходит изменение плотности и давления в газе (рис. 1). 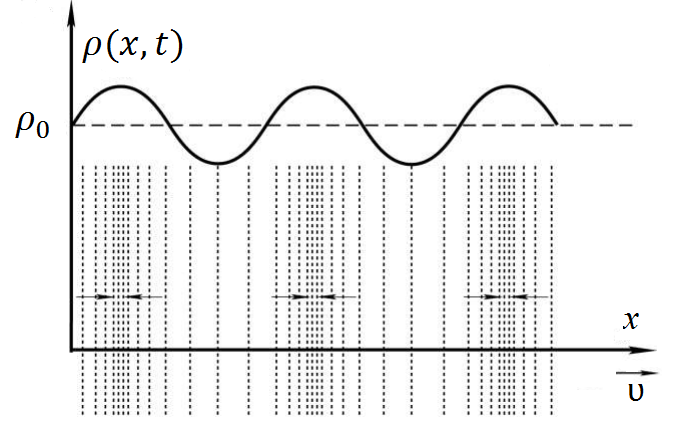 Рис.1 Эти области, перемещающиеся с определенной скоростью υ, называют звуковой волной. Звуковые волны – это процесс распространения колебаний плотности 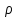 или давления или давления 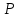 среды. Определим, от чего зависит скорость распространения звука в газовой среде, которая в состоянии равновесия при данной температуре имеет плотность среды. Определим, от чего зависит скорость распространения звука в газовой среде, которая в состоянии равновесия при данной температуре имеет плотность 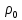 и давление и давление 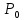 . Пусть импульс сжатия распространяется со скоростью звуковой волны υ и направлена к площадке S (рис.2). . Пусть импульс сжатия распространяется со скоростью звуковой волны υ и направлена к площадке S (рис.2). 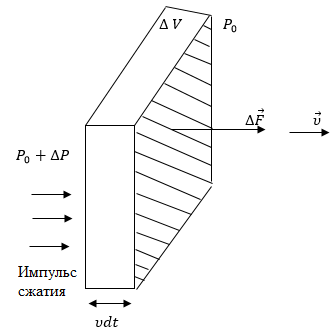 Рис.2 Волна, подходящая к площадке S увеличивает с одной стороны площадки давление на малую величину 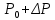 и тогда это увеличение давления приводит к появлению силы давления и тогда это увеличение давления приводит к появлению силы давления 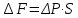 . За малое время ∆t данная сила приводит в движение избыточную ∆m массу газа с плотностью . За малое время ∆t данная сила приводит в движение избыточную ∆m массу газа с плотностью 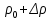 , которая находится в объёме , которая находится в объёме 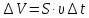 (рис.2). Данная масса газа ∆m = ∆ρ٠S٠υ∆t перемещается через площадку S со скоростью υ и образует область сжатия. (рис.2). Данная масса газа ∆m = ∆ρ٠S٠υ∆t перемещается через площадку S со скоростью υ и образует область сжатия.Из уравнения движения следует, что 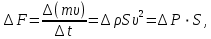 откуда, в силу малости изменений ∆ρ и ∆P, получаем откуда, в силу малости изменений ∆ρ и ∆P, получаем 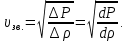 (5) (5)Процесс расширения и сжатия газа при образовании звуковой волны может быть различным. Будем считать его политропическим, т. е. имеющим постоянную молярную теплоёмкость С = const. Уравнение политропического процесса: 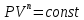 (6), где (6), где 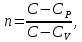 (7), здесь (7), здесь 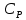 и и 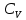 – молярные теплоёмкости газа при постоянном давлении и постоянном объёме. Учитывая, что – молярные теплоёмкости газа при постоянном давлении и постоянном объёме. Учитывая, что 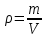 , уравнение (6) можно записать в виде , уравнение (6) можно записать в виде 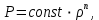 (8) (8)Тогда 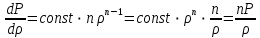 (9). Если считать газ по свойствам близким к идеальному, то можно использовать уравнение состояния идеального газа: (9). Если считать газ по свойствам близким к идеальному, то можно использовать уравнение состояния идеального газа: 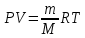 или или 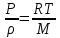 , (10) то с учётом (9) получим , (10) то с учётом (9) получим 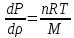 . (11) . (11) Тогда скорость звука в газе, согласно формулам (5) и (11), получим 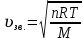 . (12) . (12)В реальности скорость звука достаточна большая величина, а процессы сжатия и разрежения газа идут настолько быстро, что теплообмен произойти не успевает, и процесс можно считать адиабатическим с показателем 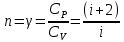 , где i – число степеней свободы молекул газа. , где i – число степеней свободы молекул газа. Таким образом, скорость звука в воздушной (газовой) среде: 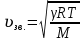 . (13) . (13)Отсюда видно, что скорость звука для данного газа зависит от температуры T равновесного состояния. Если разница температур ∆Т не слишком большая по сравнению с эталонной температурой 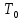 , то скорость звука будет зависит линейно от ∆Т: , то скорость звука будет зависит линейно от ∆Т: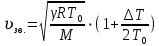 , (14) где , (14) где 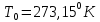 . .Если в качестве идеального газа используется сухой воздух, то скорость звука определяют следующим образом: 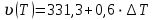 . (15) . (15) В этом опыте измеряется время распространения звукового импульса t между двумя акустическими зондами, находящимися на расстоянии s друг от друга. Звуковой импульс создаётся резким движением диффузора громкоговорителя, управляемым импульсом напряжения с крутым фронтом. Измерение времени распространения звукового импульса осуществляется с помощью микросекундного счётчика. Отсчёт времени начинается, когда звуковой импульс достигает первого акустического зонда, и заканчивается, когда он достигает второго акустического зонда, находящегося на расстоянии s. Нагревательный элемент предназначен для нагрева воздуха в трубке Кундта до 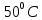 , для измерения зависимости времени распространения звука от температуры. Распределение температуры во время охлаждения является достаточно равномерным. Поэтому достаточно измерить температуру в одной точке трубки Кундта. , для измерения зависимости времени распространения звука от температуры. Распределение температуры во время охлаждения является достаточно равномерным. Поэтому достаточно измерить температуру в одной точке трубки Кундта. Для подачи в трубку Кундта технических газов, отличных от воздуха можно использовать трубный соединитель. Описание лабораторной установки:  Рис.3 Трубка Кундта Звуковая трубка из прозрачного акрилата с динамиком и подвижной шкалой для количественного исследования звуковых волн в воздухе и других газах, в частности, для измерения длин волн и скорости звука. Трубка оснащена двумя стойками, сенсорным диском, двумя патрубками с запорными кранами (патрубки предназначены для шлангов) для подачи газа, креплением и направляющей для длинного акустического зонда, а также держателем и соединительным разъёмом для нагревательного стержня К. Диапазон частоты: от 20 до 5000 Гц Длина звуковой трубки: 1000 мм Диаметр звуковой трубки: 70 мм Шкала: 950 мм Патрубки для шланга: диаметр 5 мм Выходная мощность динамика: 2 Вт Сопротивление динамика 50 Ом Вес: прибл. 1,25 кг  Рис.5 Блок формирования импульсов Электронный переключатель, выводящий электрический импульс на подключенный динамик при нажатии на кнопку. Питание подаётся от блока батарей 9 В. Размеры: прибл. 100x75x35 мм  Рис.6 Акустический зонд, длинный Маленький микрофон на конце длинного стержня. Предназначен для измерения изменений звукового давления в трубке Кундта. Имеет резьбу для крепления диска зонда трубки Кундта. Диапазон частоты: 20 Гц – 16 кГц Диаметр стержня: 6 мм Длина стержня: 810 мм Соединительный провод: Приближённо 1 м, разъём 3,5 мм  Рис.7 Акустический зонд, короткий Маленький микрофон на конце короткого стержня. Предназначен для измерения изменений звукового давления. Диапазон частоты: 20 Гц – 16 кГц, (1 – 20 Гц и 16 – 42 кГц, ненормируемый допустимый диапазон) Диаметр стержня: 6 мм Длина стержня: 140 мм Соединительный провод: приближённо 0,6 м, разъёмы 3,5 мм  Рис. 8 Усилитель для микрофонов (230 В, 50/60 Гц) или (115 В, 50/60 Гц) Многоцелевой двухканальный усилитель для длинных или коротких акустических зондов. Особенно хорошо подходит для работы с микросекундными счётчиками в опытах по определению скорости звука. Имеет подключаемый источник питания 12 В переменного тока. Рабочие режимы обоих каналов можно переключать независимо. Режим Signal предназначен для работы с осциллографом, режим Level предназначен для работы с вольтметрами, а режим Pulse – для работы с микросекундным счётчиком. Триггерный уровень импульса зависит от коэффициента усиления предварительного усилителя, который можно регулировать. Ширина полосы частот: от 10 Гц до 42 кГц Коэффициент усиления: от 20 до 70 Полное выходное сопротивление: 1 кОм Выходной сигнал: возможно переключение режима между Signal(сигнал), Level (уровень) и Pulse (импульс). Сигнал: 0–14 В полного размаха Уровень: 0–7 В постоянного тока Импульс: Низкий: 0 В, высокий: 8 В постоянного тока, длительность: 150 мс Входы: соединители 3,5 мм Выходы: гнездо BNC Питание: подключаемый к сети источник питания 12 В переменного тока, 500 мА Размеры: 100x75x35 мм Вес, вместе с источником питания: приближённо 450 г  Рис. 10 Миллисекундный счетчик (115 В, 50 / 60 Гц) или (230 B, 50/60 Гц) Каждый отсчет запускается и останавливается сигналом на входных разъемах. Устройство автоматически сбрасывается в ноль при каждом перезапуске. Измерение времени: 1 мс - 9999 с Напряжение питания: 12 В перем. тока Разъемы: 4-мм безопасные розетки Размеры: приближённо 105x75x35 мм. Вес: приближённо 400 г  Рис.11 Нагревательный стержень Нагревательный стержень для нагревания воздуха в трубке Кундта до температуры приблизительно 50°C. Рабочее напряжение: макс. 12 В Потребляемая мощность: 36 Вт Температура в трубке Кундта: максимально 50°C Разъемы: пара 4 мм Размеры: приближённо 900 мм x диаметр 11 мм  Рис. 12 Высокочастотный соединительный шнур, BNC/4-мм штекер Сопротивление: 50 Ом Длина: 1 м  Рис.13 Источник питания постоянного тока, 0 – 20 В, 0 – 5 А (230 В, 50/60 Гц) или (115 V, 50/60 Hz) Универсальный блок питания с цифровым дисплеем тока и напряжения. Выходное напряжение и выходной ток плавно регулируются. Устройство может использоваться в качестве источника постоянного напряжения с ограничением тока или в качестве источника постоянного тока с ограничением напряжения. Выход постоянного тока: 0–20 В, 0–5 А Выходная мощность: 100 Вт Стабильность при полной нагрузке ≤0,01% + 5 мВ, ≤0,2% + 5 мА Остаточная пульсация ≤1 мВ, 3 мА Дисплей: 2 х 3-разрядные светодиодные клеммы: 4 мм безопасные розетки Размеры: прибл. 130x150x300 мм Вес: ок. 4,7 кг  Рис. 14 Цифровой быстродействующий карманный термометр Предназначается для мгновенных измерений на поверхностях, в жидкостях, мягких пластичных средах, воздухе / газах, на очень мелких объектах. Рассчитан на подключение к никель-хром-никелевому измерительному датчику типа K. Датчик не входит в комплект поставки. Диапазон измерения: -65°C–1150°C / -85°F–1999°F в 2 диапазонах Цена деления: 0,1°C / 1°C/F Погрешность в нижнем диапазоне: 0,05% от измеряемого значения, 0,2% полной шкалы Индикатор: ЖК-индикатор, 31/2-разрядный, высота 13 мм Размеры: 106x67x30 мм3 Вес: приближённо 135 г  Рис. 15 Никель-хром-никелевый погружной датчик типа K с диапазоном измерения от –65°C до 550°C Датчик для измерения температуры с трубкой из нержавеющей стали (V4A), подпружиненный (жесткий), с силиконовым кабелем. Диапазон измерения: -65°C–550°C Время отклика: прибл. 3 с Трубка: 130 мм x диам. 1,5 мм  Рис. 16 Пара безопасных соединительных проводов для опытов длиной 75 см Набор из двух медных проводов с очень гибкой изоляцией из поливинил хлорида, длиной 75 см, черный, со складными 4-миллиметровыми безопасными многослойными заглушками на обоих концах. Сечение проводника: 2,5 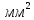 Напряжение: безопасное сверхнизкое напряжение Максимум. длительный ток: 32 А Порядок выполнения лабораторной работы: Собрать установку и подключить к источнику питания. Подключить блок формирования импульсов напряжения к динамику. Установить датчики-микрофоны (зонды). Выставить расстояние между ними в 10 см и изменяя это расстояние с шагом по 10 см, получить 8-10 измерений при комнатной температуре. По полученным экспериментальным значениям построить график зависимости расстояния s от времени t распространения звука в воздухе при комнатной температуре. Определить величину средней скорости звука в воздухе при данной температуре. Найти абсолютную и относительную погрешности измерений. Установить нагревательный элемент, датчик температуры, подключить источник питания и нагреть воздух в трубке Кундта на 5 градусов. Нагревая с интервалом в 5 градусов, получить 6-8 измерений скорости звука для различных температур. По полученным результатам построить график зависимости скорости звука υ (м/с) от температуры 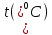 , согласно формулам 13 и 15. , согласно формулам 13 и 15.При наличии других газов, проделать пункты 1 – 8 для выбранного газа. Обработка результатов измерений: Составте таблицу и занесите полученные экспериментальные данные в таблицу. По полученным экспериментальным значениям вычислите величину среднего арифметического скорости звука. Сравните полученное значение средней скорости звука с величиной полученной по формуле 13. Определите величину случайной ошибки 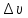 . .Определите относительную ошибку измерений δ (%). Сделайте выводы по результатам лабораторной работы. Контрольные вопросы: Что называется, механической волной? Какая волна является продольной? Поперечной? Получите уравнение плоской бегущей монохроматической волны. Объясните физический смысл всех входящих в уравнение волны величин. Напишите волновое уравнение. Укажите его отличие от уравнения волны. Как связаны между собой скорость распространения волны с частотой и длиной волны? Какими свойствами обладают механические волны? Что называется, звуком? От чего зависит скорость распространения звуковой волны в твердых, жидких и газообразных веществах? Что называется, высотой звука? От чего зависит громкость звука? В чем заключается метод измерения длины звуковой волны, применяемый в данной лабораторной работе? Список литературы: 1. Савельев И.В. Курс общей физики в 4-х томах. Механика. Молекулярная физика и термодинамика. – М.: КноРус, 2012. – Т.1. – 528 с. 2. Сивухин Д.В. Общий курс физики. Механика. – М.: МФТИ, 2010. – Т.1. – 560 с. 3. Трофимова Т.И. Курс физики. – 20-е изд., стер. – М.: Изд-во «Академия», 2014. – 560 с. 4. Яворский Б.М., Детлаф А.А. Курс физики. 9-е изд., М.: Изд-во «Академия», 2014.–720 с. 5. Яворский Б.М., Детлаф А.А. Справочник по физике. – 8-е изд., М.: Изд-во «Оникс», 2008. – 1056 с. |
