|
|
Лабораторная работа 110 введение
ВОЛНЫ
Колеблющееся материальное тело, помещенное в упругую среду, увлекает за собой и приводит в колебательное движение прилегающие к нему частицы среды. Благодаря наличию упругих связей между частицами колебания распространяются с характерной для данной среды скоростью по всей среде.
Процесс распространения колебаний в упругой среде называется волной. Различают два основных типа волн: продольные и поперечные. В продольных волнах частицы среды колеблются вдоль направления распространения волны, а в поперечных – перпендикулярно к направлению распространения волны. Не во всякой упругой среде возможно распространение поперечной волны. Поперечная упругая волна возможна лишь в таких средах, в которых имеет место упругая деформация сдвига. Например, в газах и жидкостях распространяются только продольные упругие волны (звук).
Геометрическое место точек среды, до которых к данному моменту времени дошло колебание, называется фронтом волны. Фронт волны отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникали. В зависимости от формы фронта различают волны плоские, сферические, цилиндрические и т.д.
Уравнение плоской волны, распространяющейся без потерь в однородной среде, имеет вид
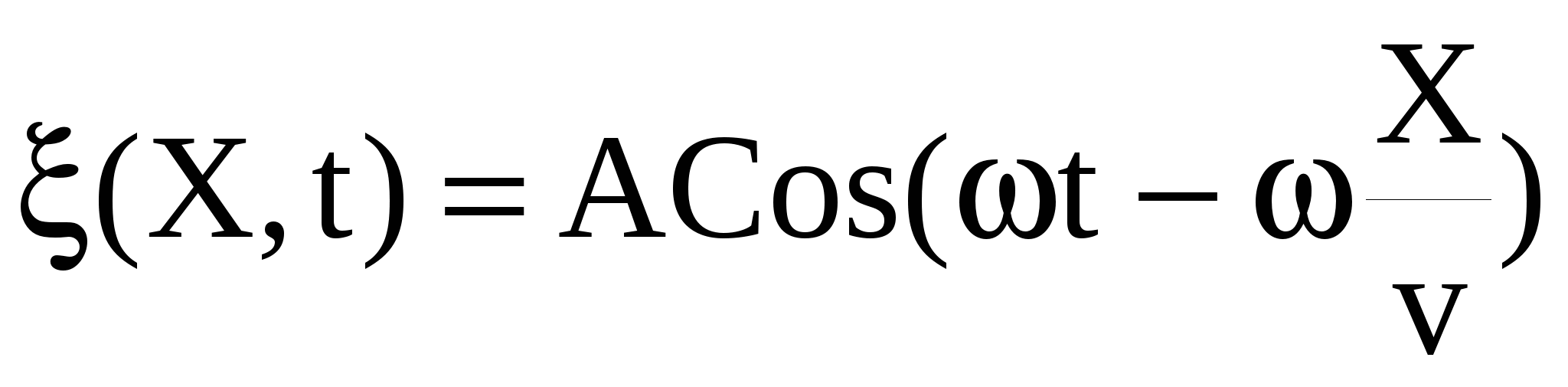 , (42) , (42)
где ξ(Х,t) – смещение частиц среды с координатой Х от положения равновесия в момент времени t, А – амплитуда, 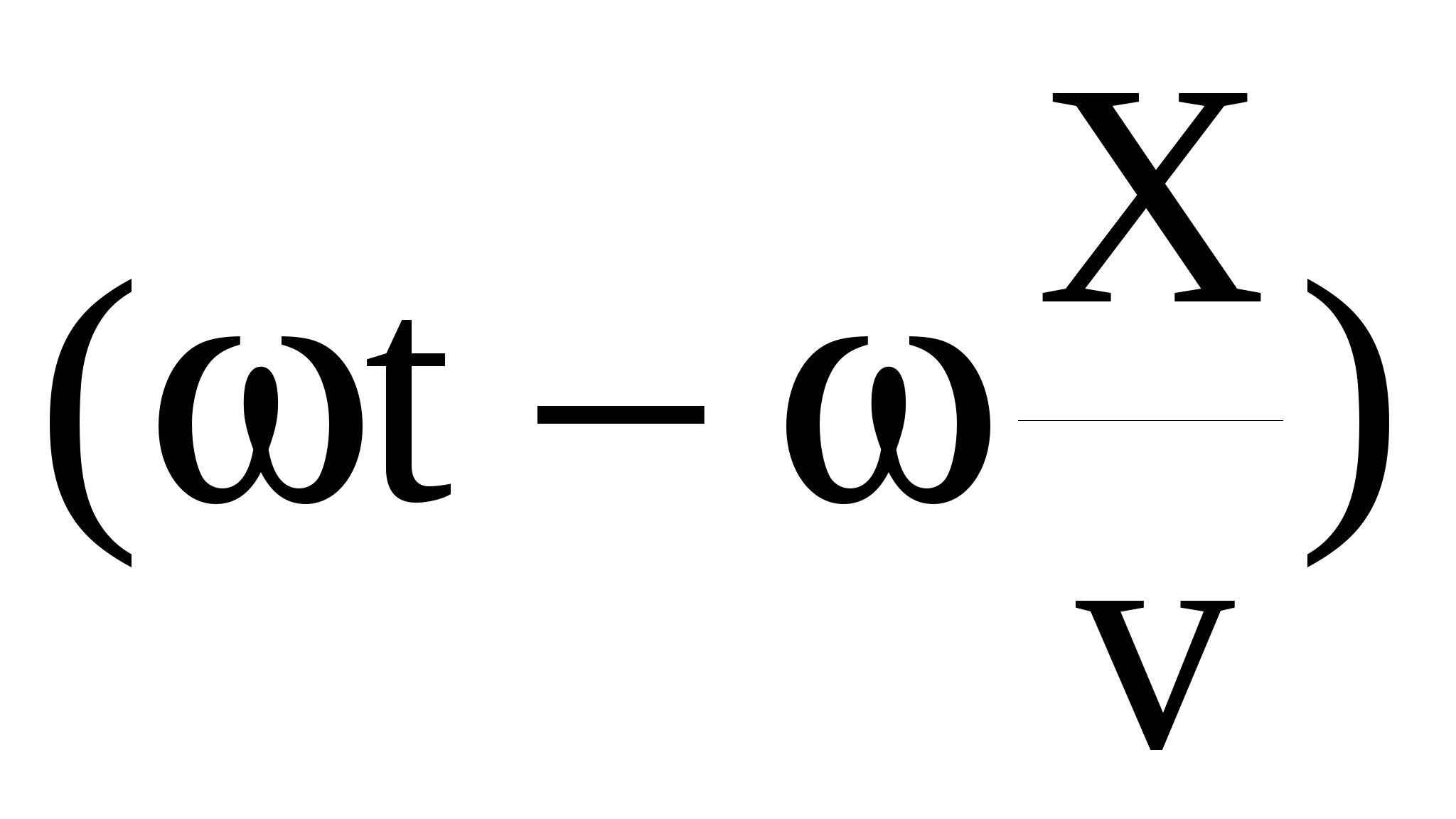 - фаза волны, - фаза волны, 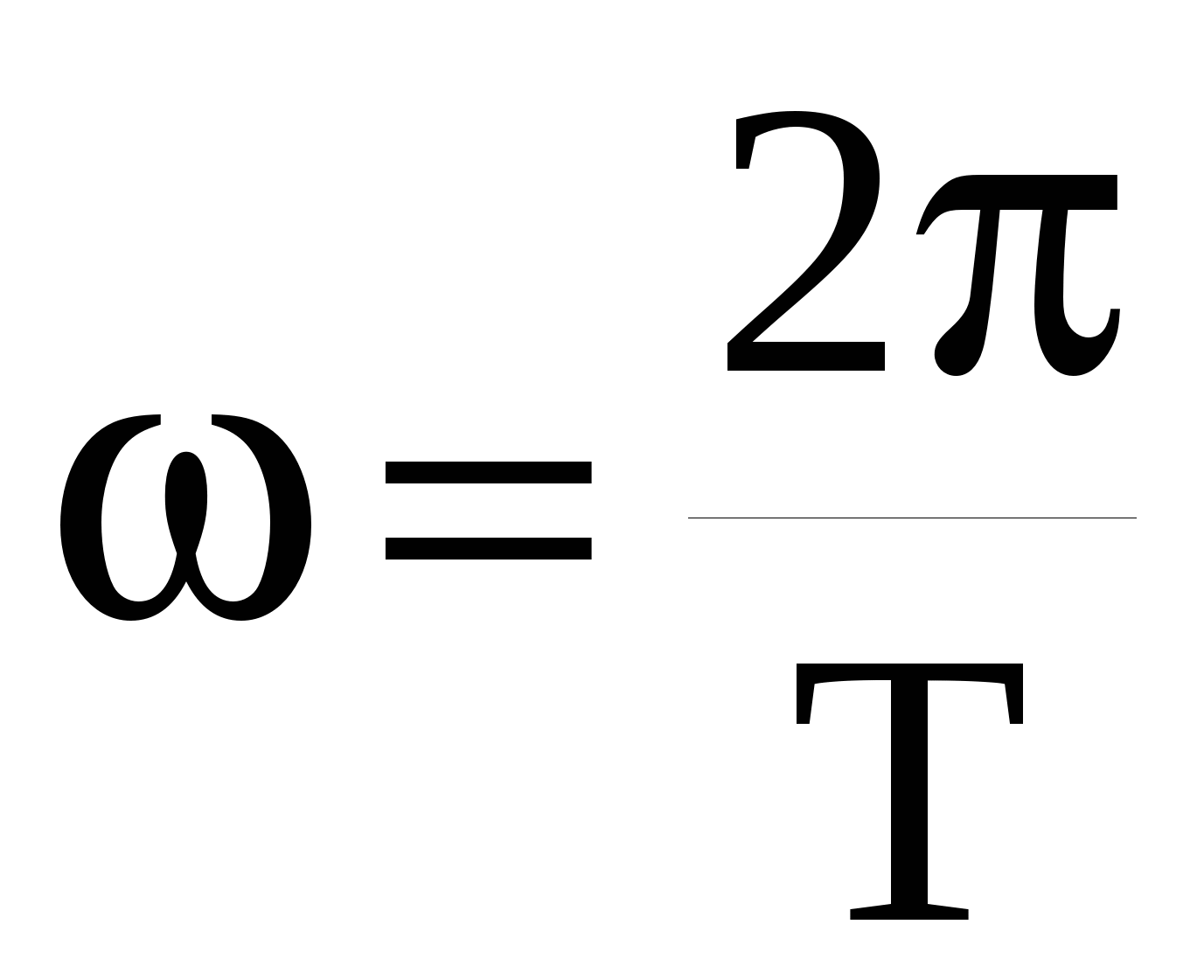 - круговая частота колебания частиц среды, v – скорость распространения волны. - круговая частота колебания частиц среды, v – скорость распространения волны.
Длиной волны λ называется расстояние между точками, колеблющимися с разностью фаз 2π, другими словами, длиной волны называется путь, проходимый любой фазой волны за один период колебаний:
λ = vT, (43)
фазовая скорость, т.е. скорость распространения данной фазы:
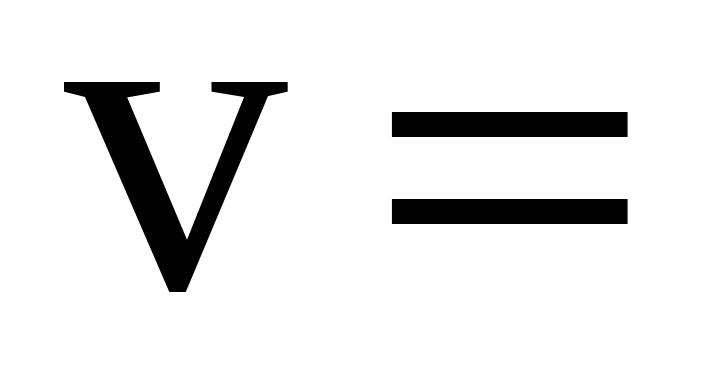 λ / Т (44) λ / Т (44)
Волновое число – число длин волн, укладывающихся на длине 2π единиц:
k = ω / v = 2π / λ. (45)
Подставляя эти обозначения в (42), уравнение плоской бегущей монохроматической волны можно представить в виде
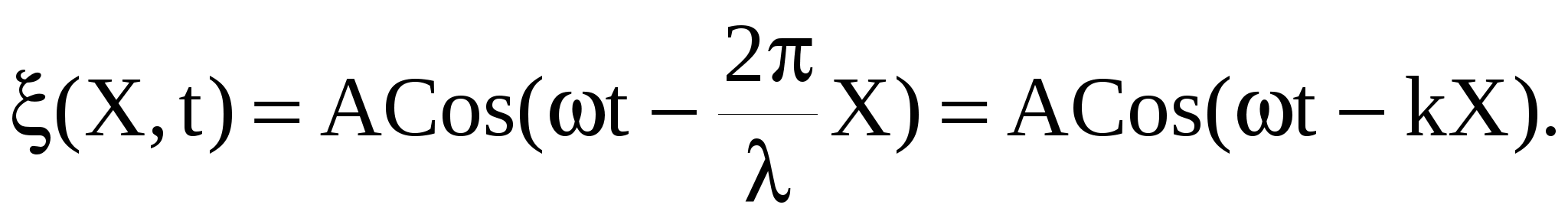 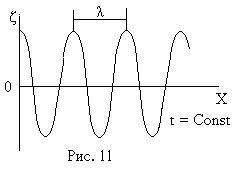
(46)
Отметим, что уравнение волны (46) обнаруживает двойную периодичность по координате и времени. Действительно, фазы колебаний совпадают при изменении координаты на λ и при
изменении времени на Т (период). Поэтому изобразить графически волну на плоскости нельзя. Часто фиксируют время t и на графике представляют зависимость смещения ξ от координаты Х, т.е. мгновенное распределение смещений частиц среды вдоль направления распространения волны (рис.11). Разность фаз Δφ колебаний точек среды зависит от расстояния ΔХ =Х2 – Х1 между этими точками
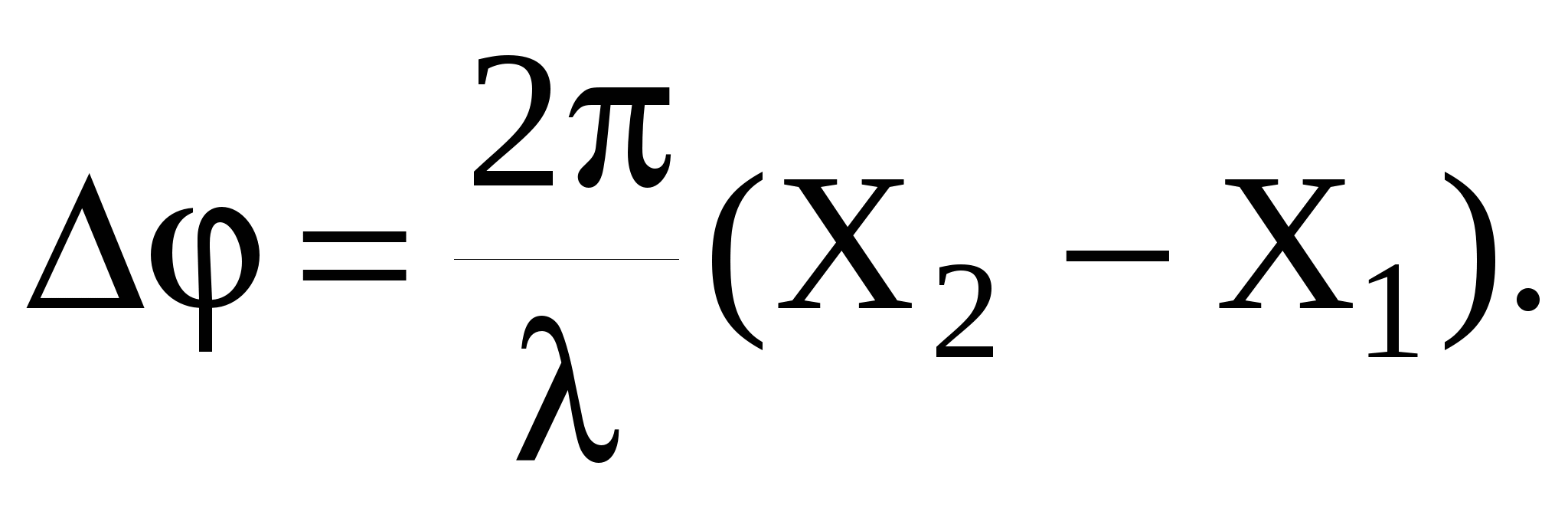 (47) (47)
Если волна распространяется противоположно направлению Х, то уравнение обратной волны запишется в виде:
ξ (Х,t) = АСos(ωt + kX). (48)
СТОЯЧИЕ ВОЛНЫ – это результат особого вида интерференции волн. Они образуются при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.
Уравнения двух плоских волн, распространяющихся вдоль оси Х в противоположных направлениях, имеют вид:
ξ1 =АСos(ωt – kX)
ξ2 = AСos(ωt + kX). (49)
Складывая эти уравнения по формуле суммы косинусов и учитывая, что k = 2π / λ, получим уравнение стоячей волны
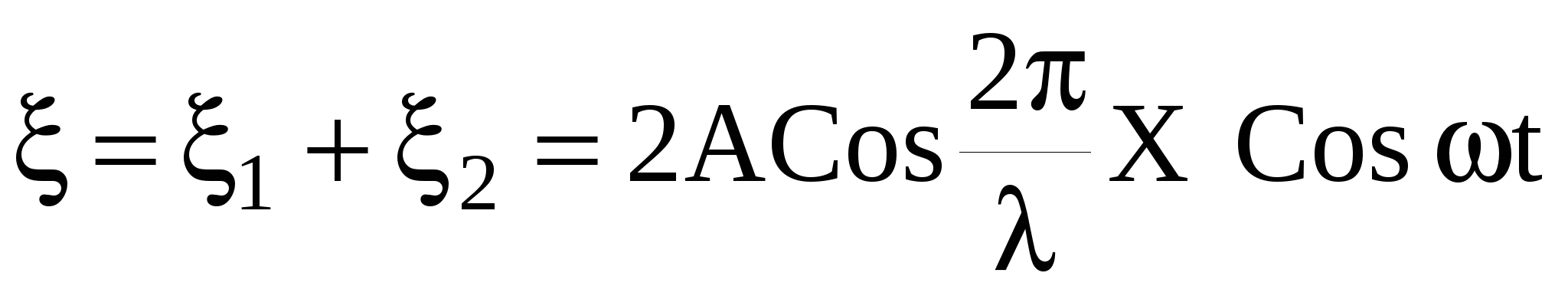 . (50) . (50)
Множитель Сos ωt показывает, что в точках среды возникает колебание той же частоты ω с амплитудой 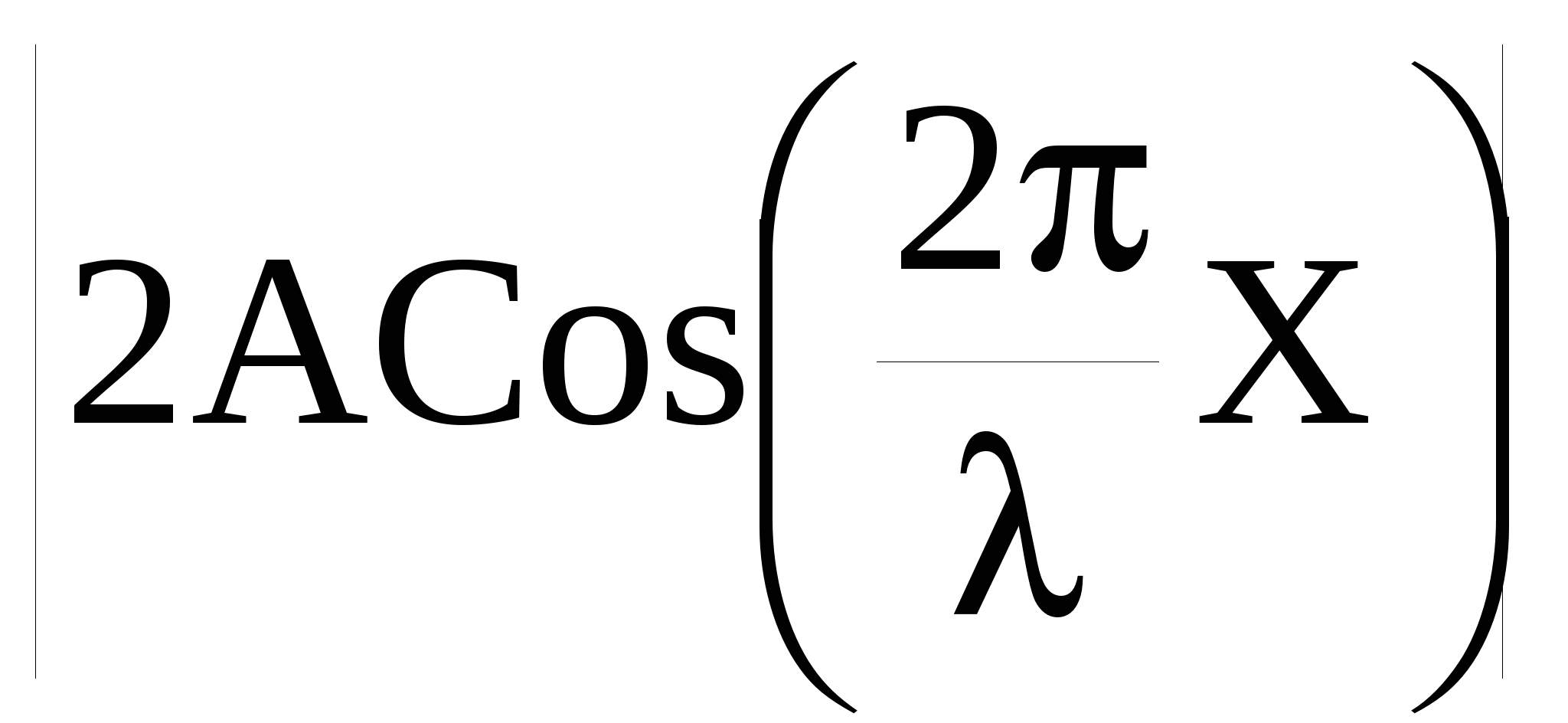 , зависящей от координаты Х рассматриваемой точки. В точках среды, где , зависящей от координаты Х рассматриваемой точки. В точках среды, где
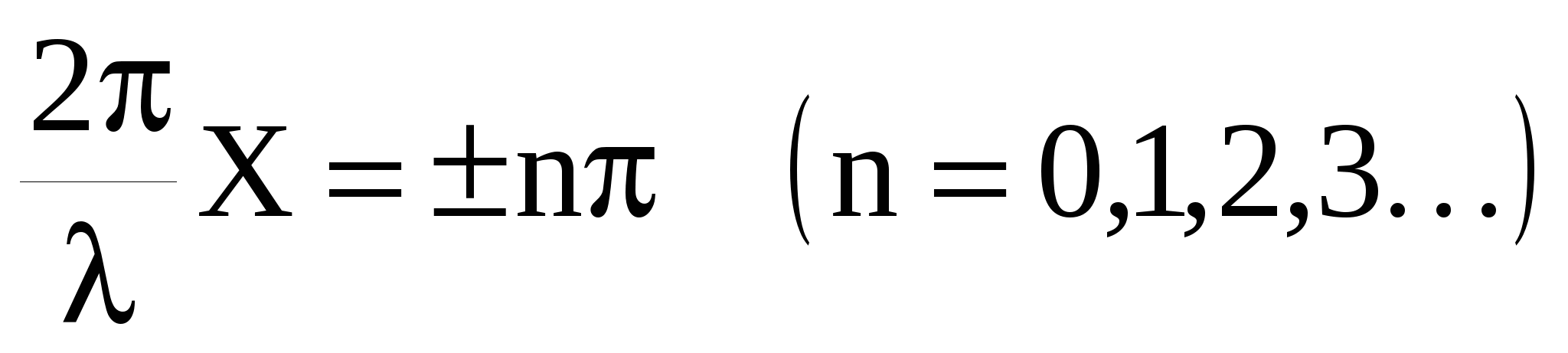 , (51) , (51)
амплитуда колебаний достигает максимального значения, равного 2А. Эти точки называются пучностями. Из выражения (51) можно найти координаты пучностей:
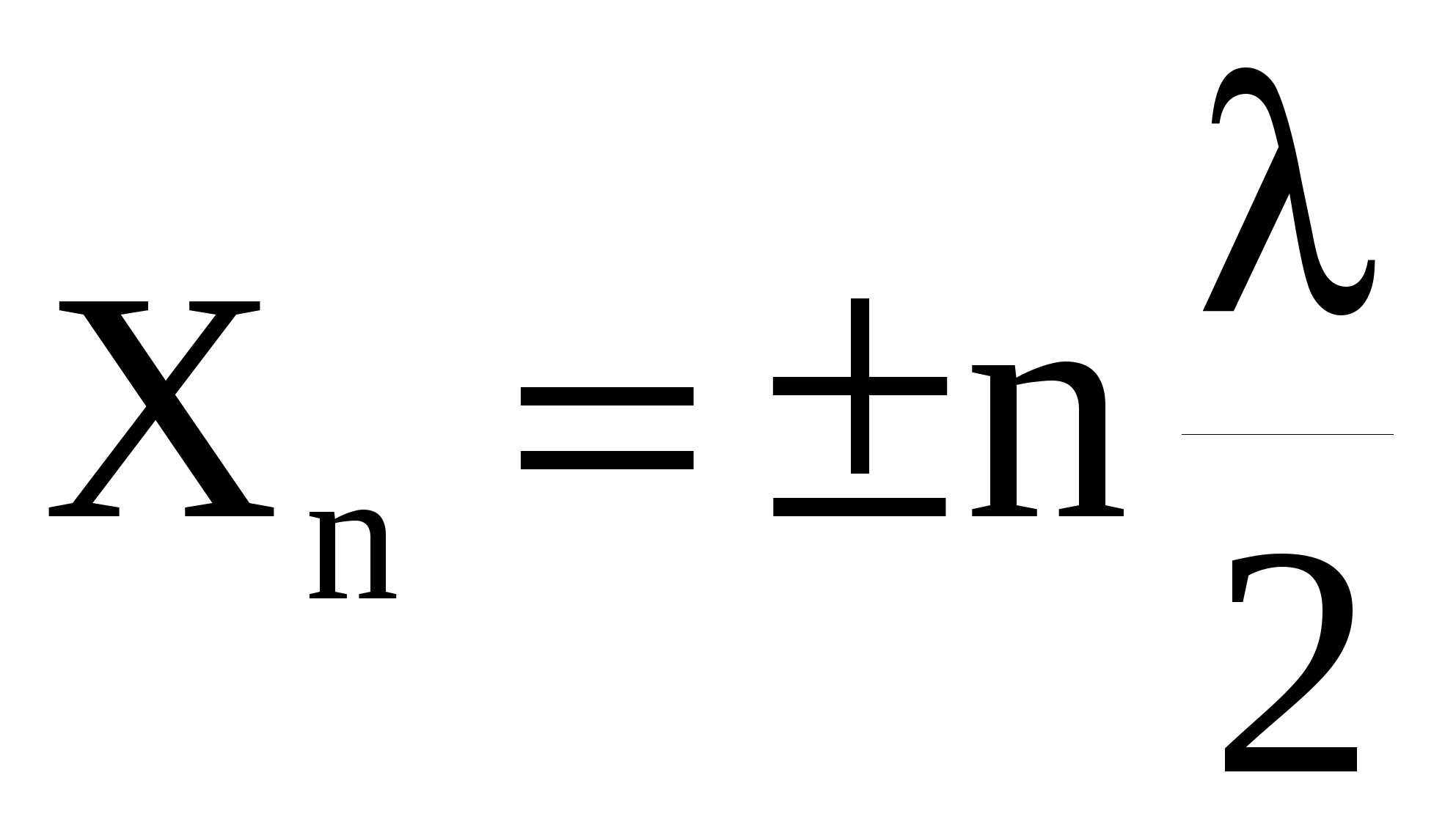 (52) (52)
В точках, где 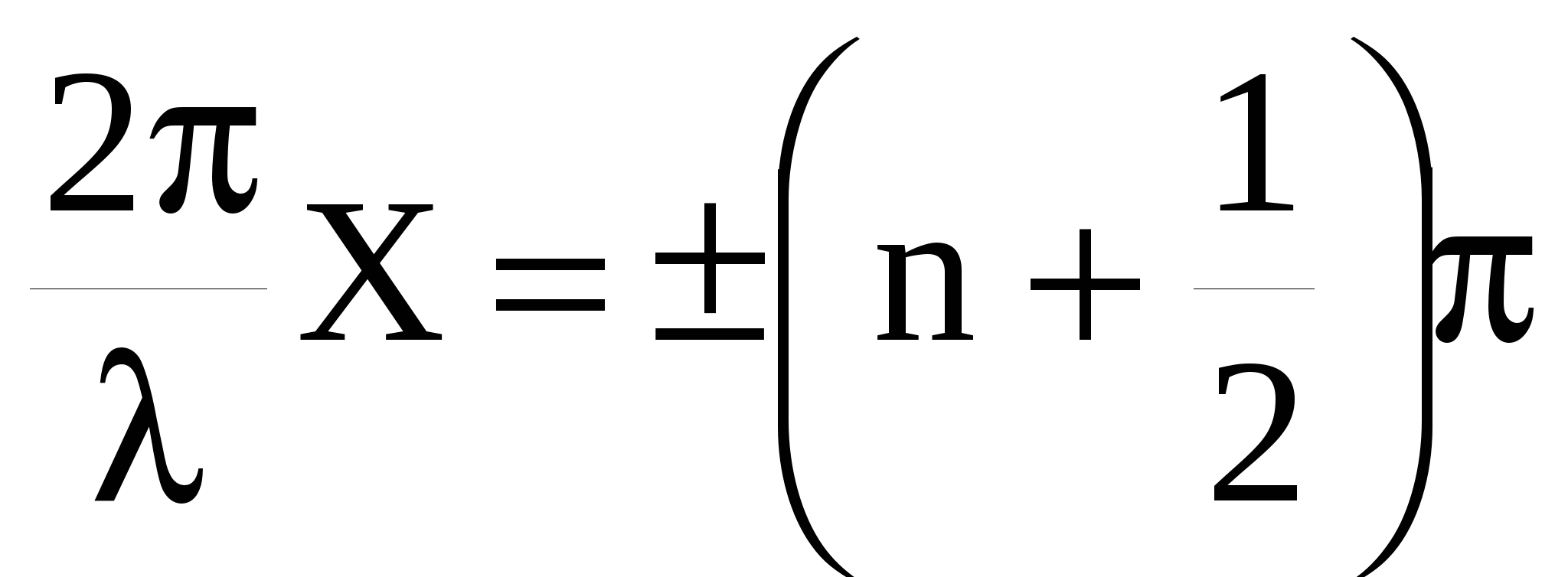 , (53) , (53)
амплитуда колебаний обращается в нуль. Эти точки называются узлами. Координаты узлов
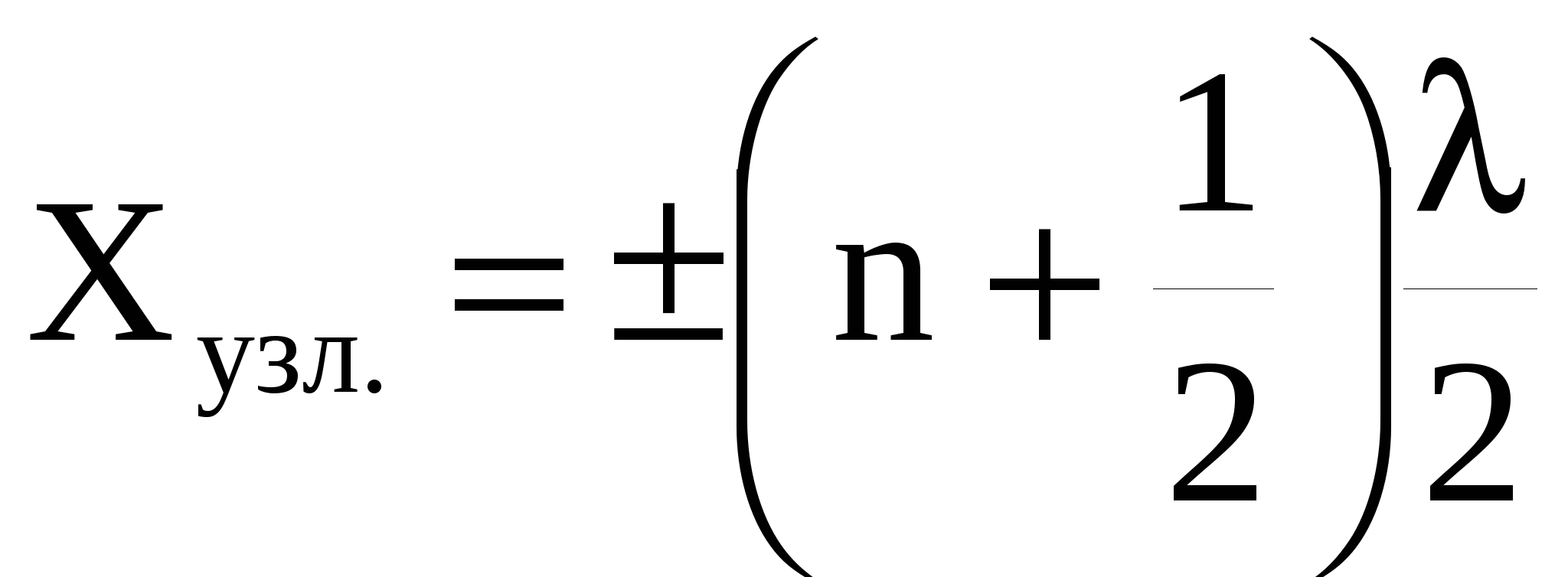 . (54) . (54)
Р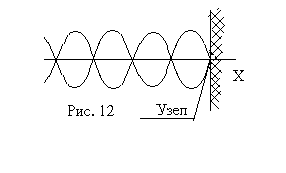
асстояния между соседними пучностями и соседними узлами одинаковы и равны λ/2. Расстояние между узлом и соседней пучностью равно λ / 4. При переходе через узел множитель 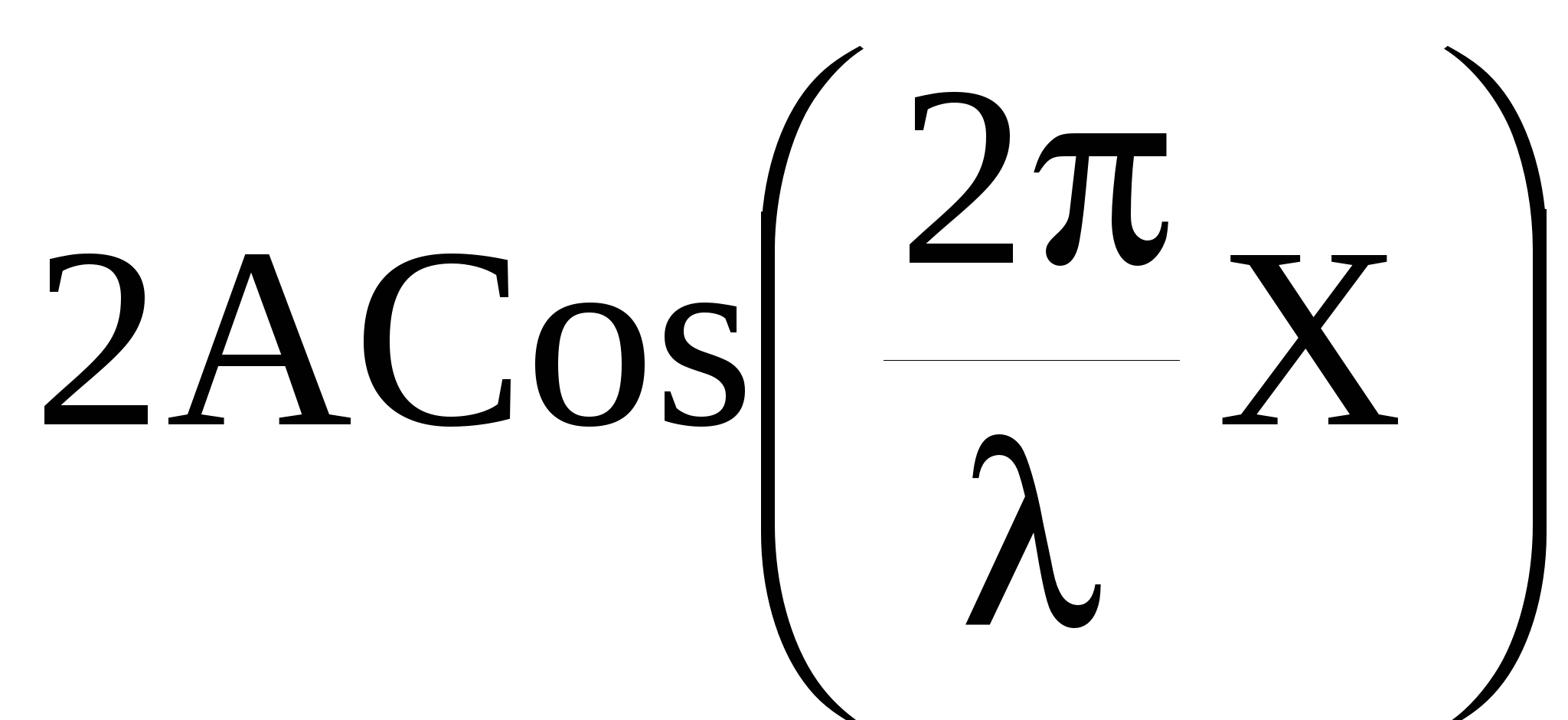 меняет знак, поэтому фазы колебаний по разные стороны от узла отличаются на π, т.е. точки, лежащие по разные стороны от узла, колеблются в противофазе. Точки, заключенные между двумя соседними узлами, колеблются с разными амплитудами, но с одинаковыми фазами. меняет знак, поэтому фазы колебаний по разные стороны от узла отличаются на π, т.е. точки, лежащие по разные стороны от узла, колеблются в противофазе. Точки, заключенные между двумя соседними узлами, колеблются с разными амплитудами, но с одинаковыми фазами.
Распределение узлов и пучностей в стоячей волне зависит от условий, имеющих место на границе раздела двух сред, от которой происходит отражение. Если отражение волны происходит от среды более плотной, то фаза колебаний в месте отражения волны меняется на противоположную или, как говорят, теряется половина волны. Поэтому, в результате сложения колебаний противоположных направлений смещение на границе равно нулю, т.е. имеет место узел (рис. 12). При отражении волны от границы менее плотной среды фаза колебаний в месте отражения остается без изменения и у границы складываются колебания с одинаковыми фазами – получается пучность. При отражении волны от границы менее плотной среды фаза колебаний в месте отражения остается без изменения и у границы складываются колебания с одинаковыми фазами – получается пучность.
В стоячей волне нет перемещения фаз, нет распространения волны, нет переноса энергии, с чем и связано название такого типа волн.
 (28) (28)
называется логарифмическим декрементом затухания. Здесь, Ne – число колебаний, совершаемых за время уменьшения амплитуды в е раз, т.е. за время релаксации.
Таким образом, логарифмический декремент затухания есть величина, обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается в е раз.
Скорость уменьшения энергии колебательной системы характеризуется добротностью Q. Добротностью колебательной системы называется величина, пропорциональная отношению полной энергии Е(t) колебательной системы к энергии (- Е), теряемой за период Т: Е), теряемой за период Т:
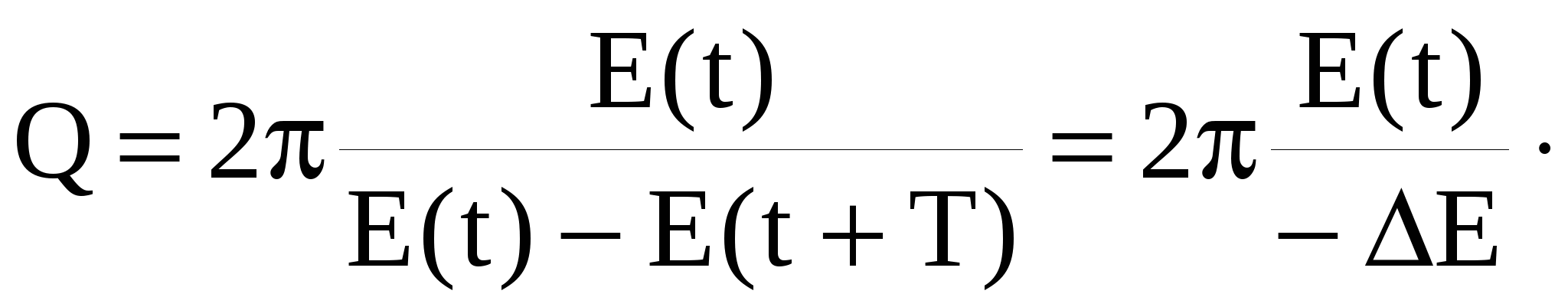 (29) (29)
Полная энергия колебательной системы в произвольный момент времени и при любом значении Х имеет вид
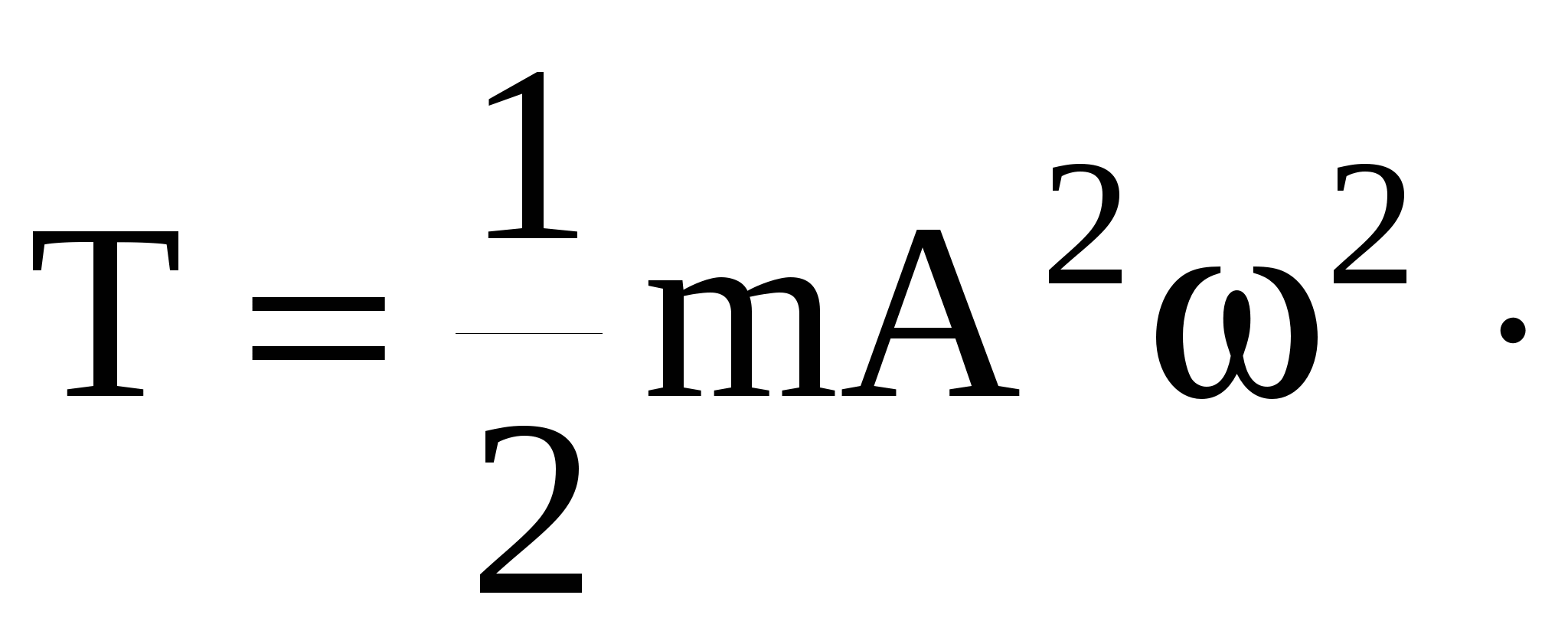 (30) (30)
Так как энергия пропорциональна квадрату амплитуды, энергия затухающих колебаний уменьшается пропорционально величине 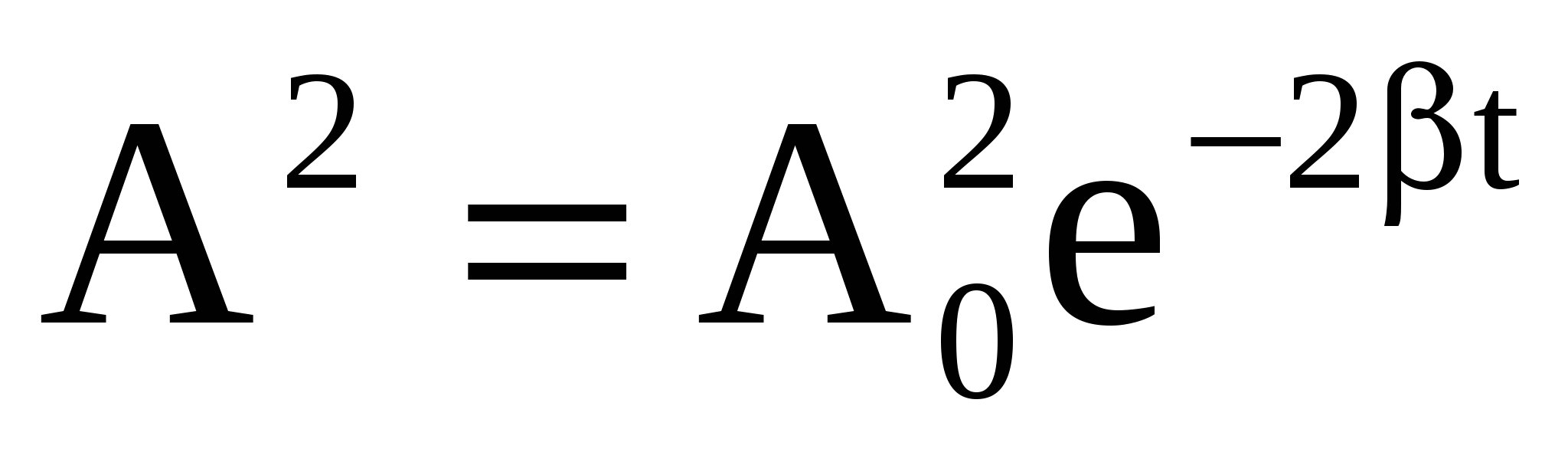 , можно написать , можно написать
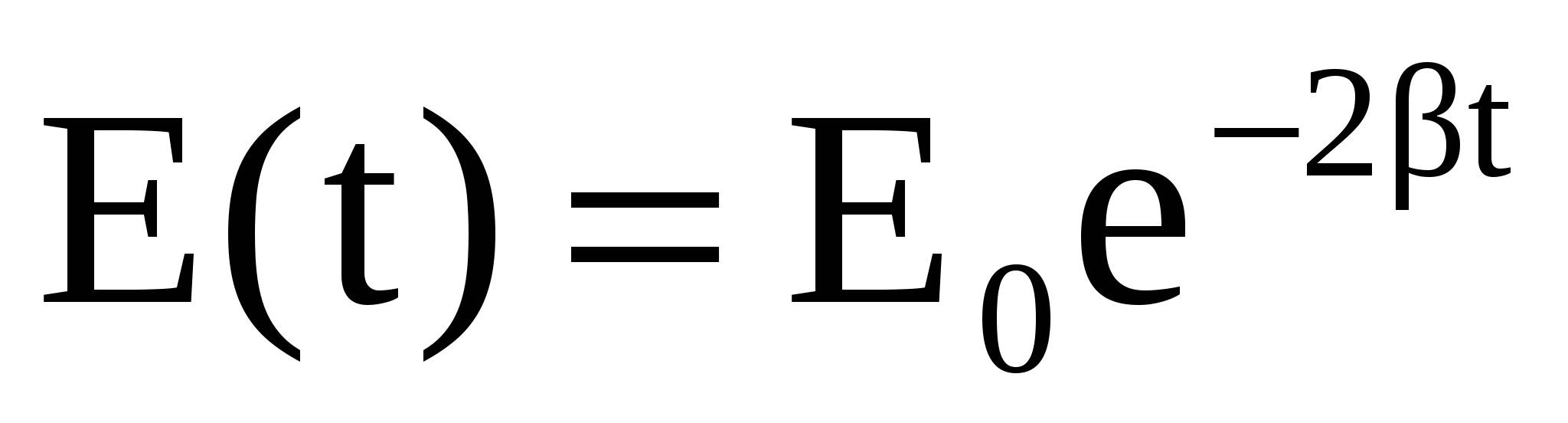 . (31) . (31)
Тогда, согласно определению, выражение для добротности колебательной системы будет иметь вид
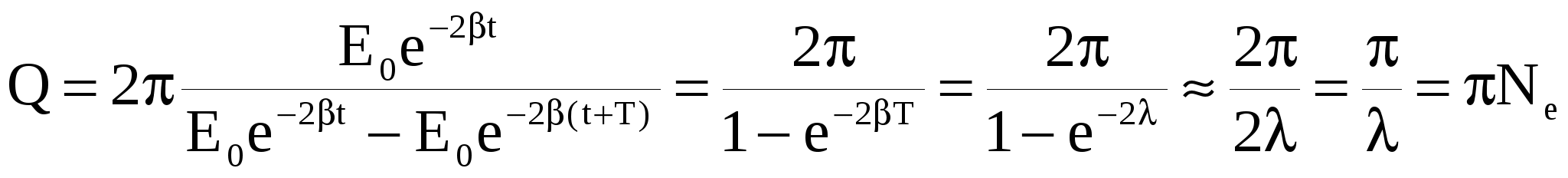 . (32) . (32)
Здесь учтено, что при малых затуханиях (1): 1-е-2 2.
Следовательно, добротность пропорциональна числу колебаний Ne, совершаемых системой за время релаксации.
Добротность колебательных систем может сильно различаться, например, добротность физического маятника Q
102, а добротность атома, который тоже является колебательной системой, достигает Q
108.
В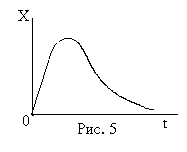
заключение отметим, что при коэффициенте затухания β=ω0 период становится
бесконечным Т =∞ (критическое затухание). При дальнейшем увеличении β период Т становится мнимым, а затухание движения происходит без колебаний, как говорят, апериодически. Этот случай движения изображен на рис.5. Критическое затухание (успокоение) происходит за минимальное время и имеет важное значение в измерительных приборах , например, в баллистических гальванометрах.
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ И РЕЗОНАНС
Если на тело с массой m действуют упругая сила Fу = -kX, сила трения 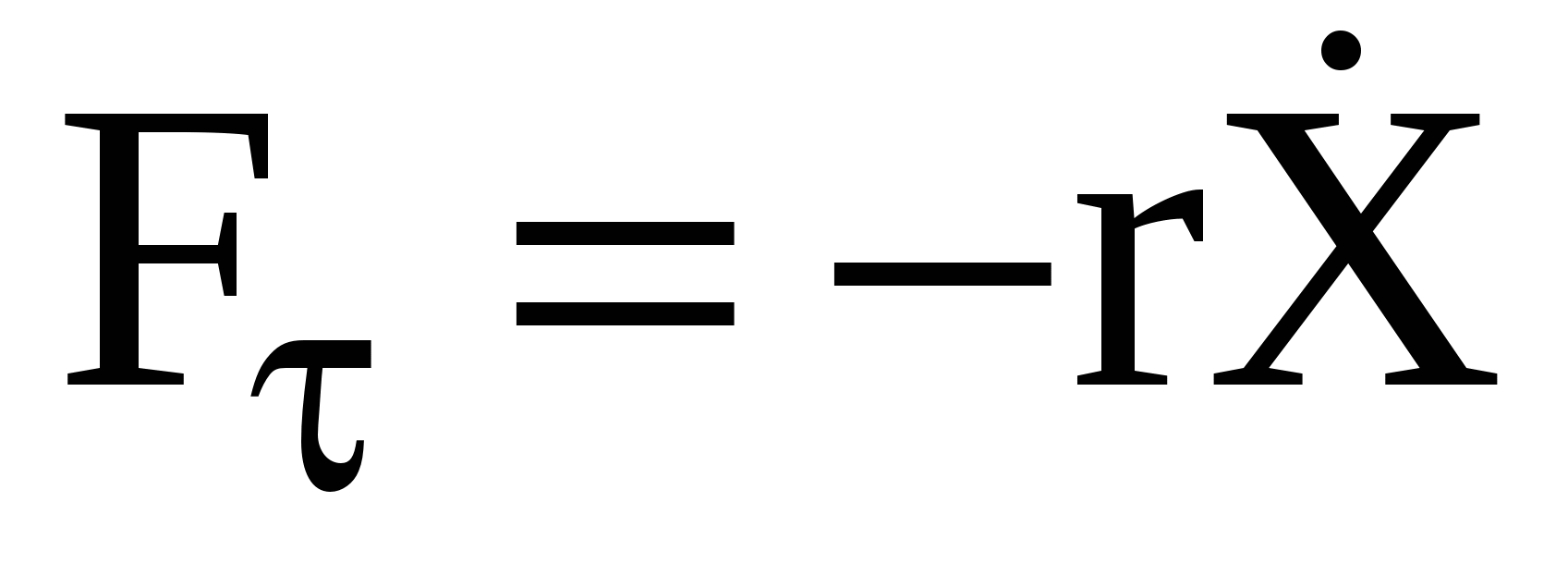 и внешняя периодическая сила и внешняя периодическая сила  , то оно совершает вынужденные колебания. В этом случае дифференциальное уравнение движения имеет вид , то оно совершает вынужденные колебания. В этом случае дифференциальное уравнение движения имеет вид
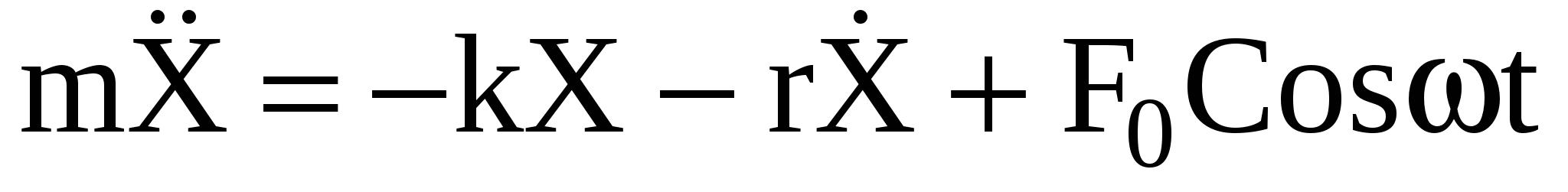 , или , или , (33) , (33)
где , , 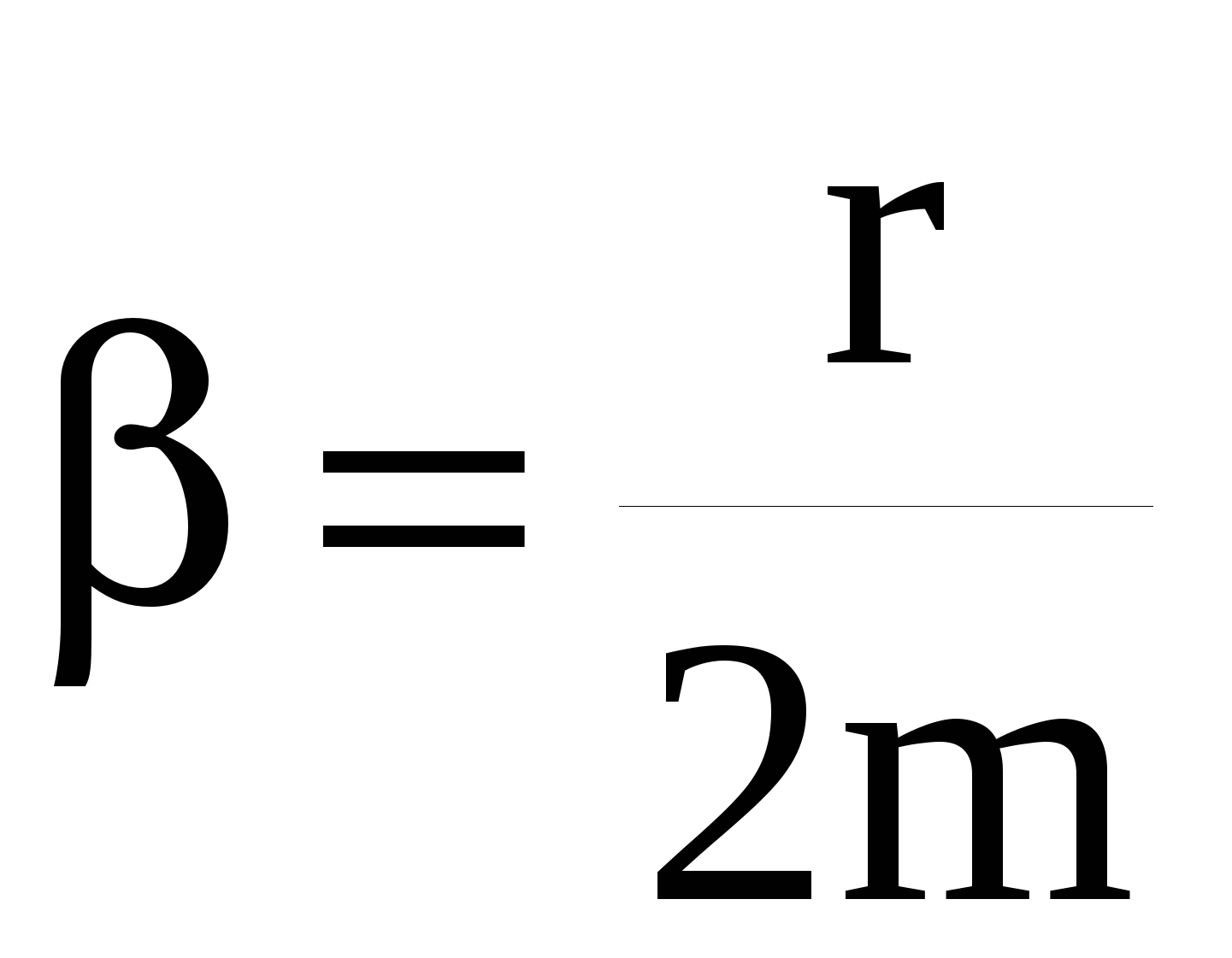 - коэффициент затухания, - коэффициент затухания, - собственная частота свободных незатухающих колебаний тела, F0 – амплитуда, ω – частота периодической силы. - собственная частота свободных незатухающих колебаний тела, F0 – амплитуда, ω – частота периодической силы.
В начальный момент времени работа внешней силы превосходит энергию, которая расходуется на трение (рис. 6). Энергия и амплитуда колебаний тела будет возрастать до тех
п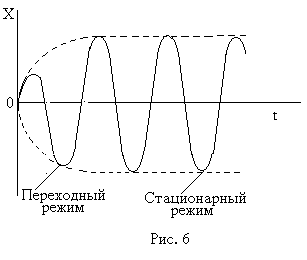
ор, пока вся сообщаемая внешней силой энергия не будет целиком расходоваться на преодоление трения, которое пропорционально скорости. Поэтому устанавливается равновесие, при котором сумма кинетической и потенциальной энергии оказывается постоянной. Это условие характеризует стационарное состояние системы.
В таком состоянии движение тела будет гармоническим с частотой, равной частоте внешнего возбуждения, но вследствие инерции тела его колебания будут сдвинуты по фазе по отношению к мгновенному значению внешней периодической силы:
 X = AСos(ωt + φ). (34) X = AСos(ωt + φ). (34)
В отличие от свободных колебаний амплитуда А и фаза вынужденных колебаний
зависят не от начальных условий движения, а будут определяться только свойствами колеблющейся системы, амплитудой и частотой вынуждающей силы:

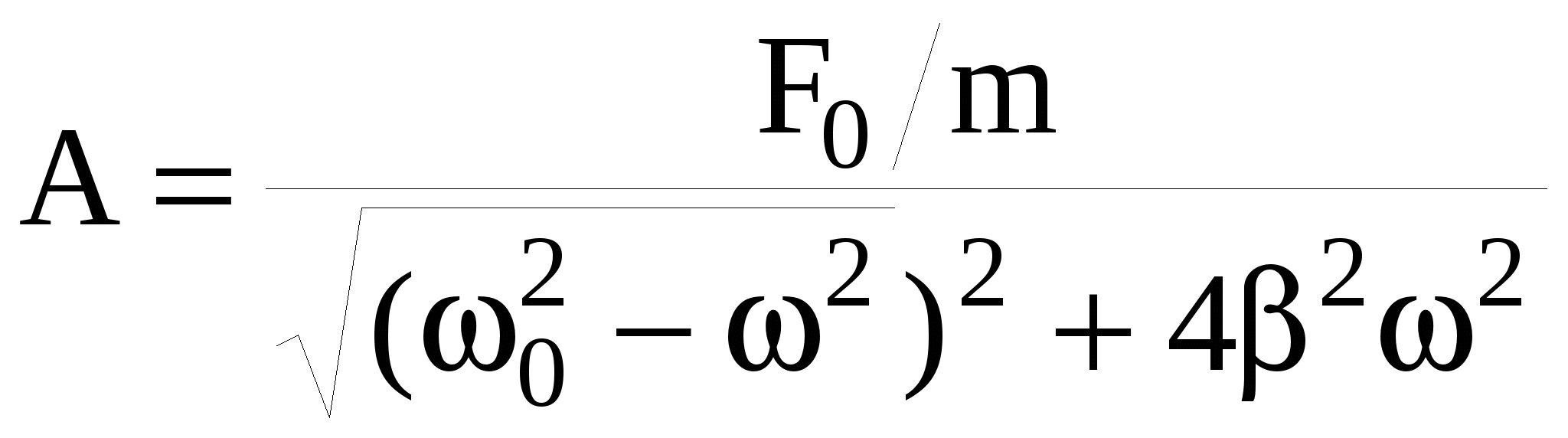 , (35) , (35)
 . (36) . (36)
Видно, что амплитуда и сдвиг по фазе зависят от частоты вынуждающей силы (рис.7 и 8).
Характерной особенностью вынужденных колебаний является наличие резонанса. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте свободных незатухающих колебаний тела ω0 носит название механического резонанса. Амплитуда колебаний тела при резонансной частоте 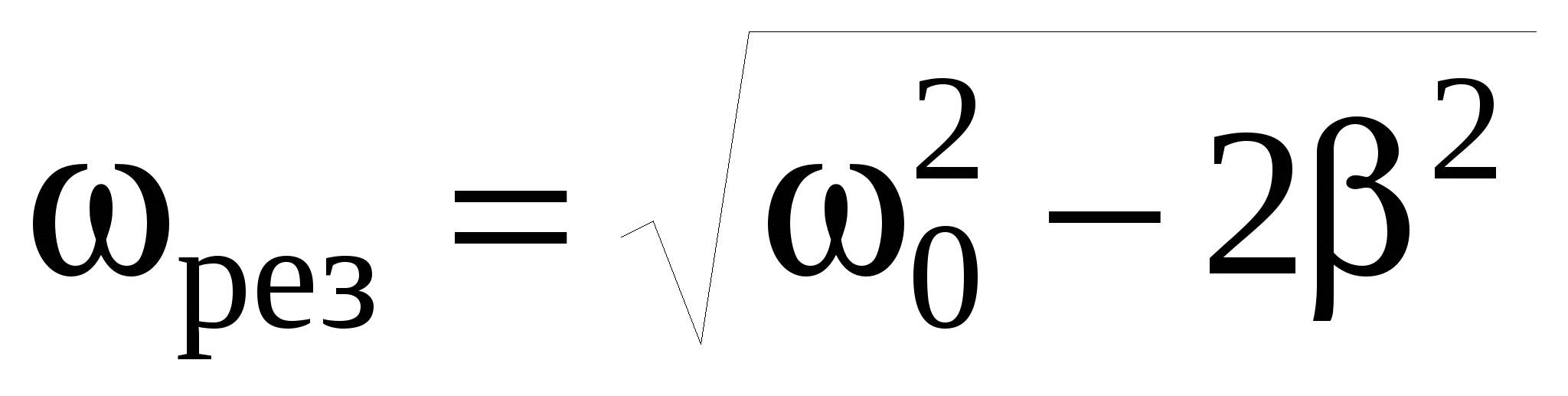 достигает максимального значения: достигает максимального значения:
 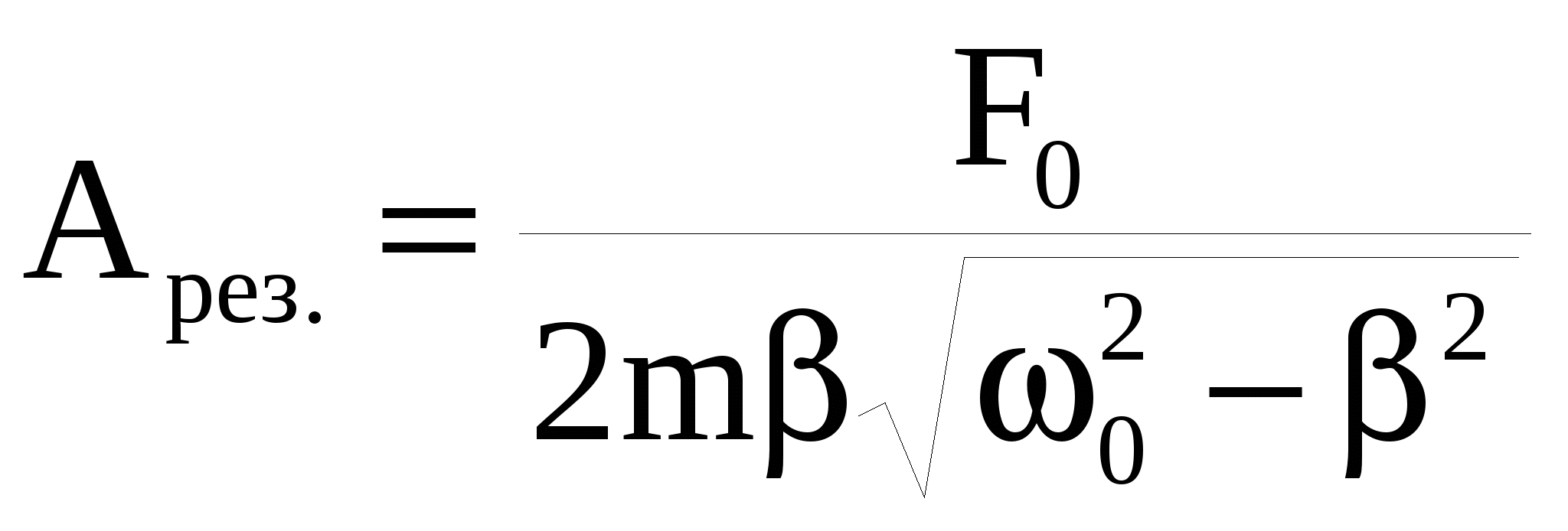 (37) (37)
По поводу резонансных кривых (см. рис. 7) сделаем следующие замечания. Если ω→ 0, то все кривые (см. также (35)) приходят к одному и тому же, отличному от нуля, предельному значению 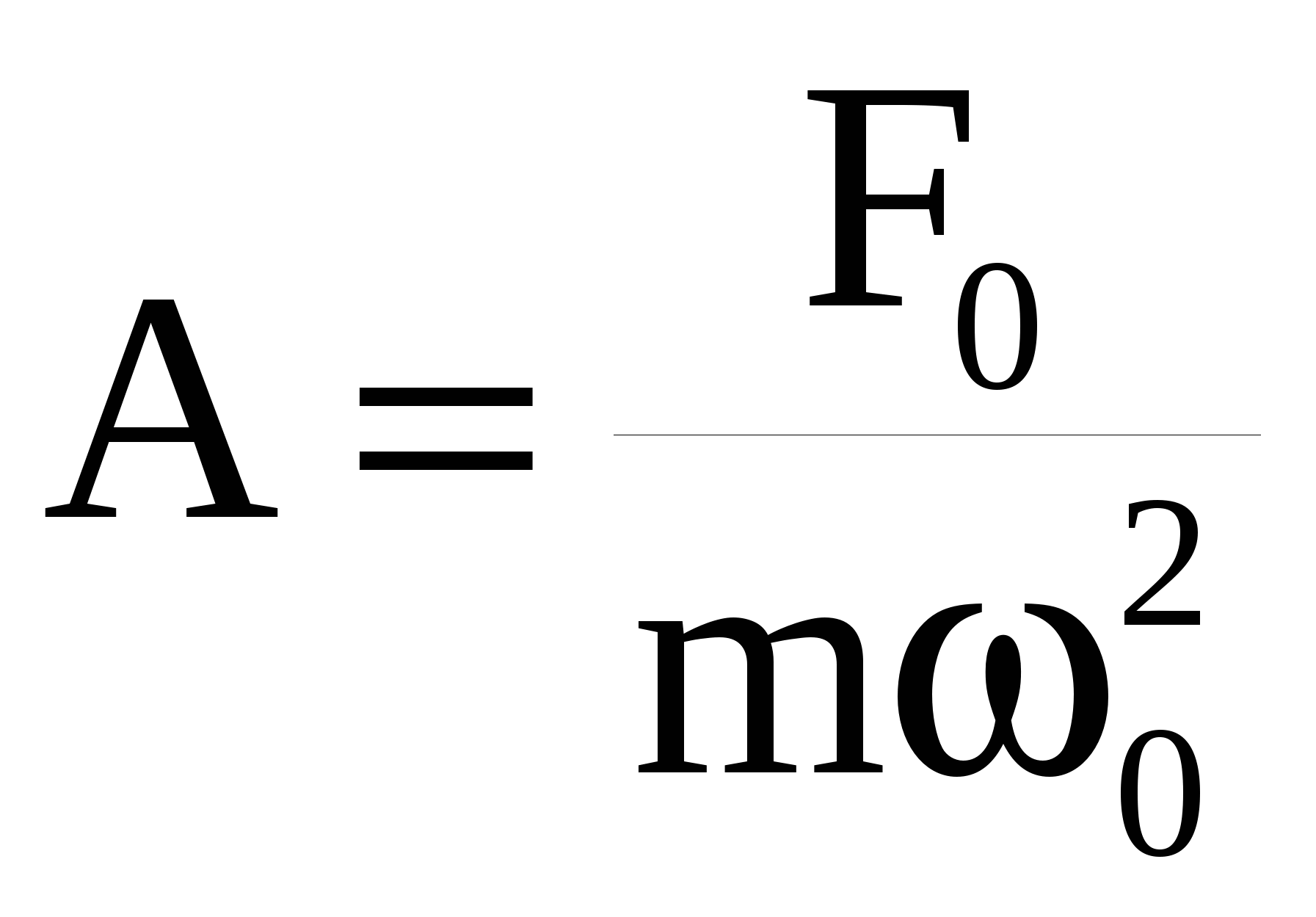 , так называемому статистическому отклонению. Если ω→ ∞, то все кривые асимптотически стремятся к нулю. , так называемому статистическому отклонению. Если ω→ ∞, то все кривые асимптотически стремятся к нулю.
При условии малого затухания (β2 ‹‹ω02) резонансная амплитуда (см.(37))
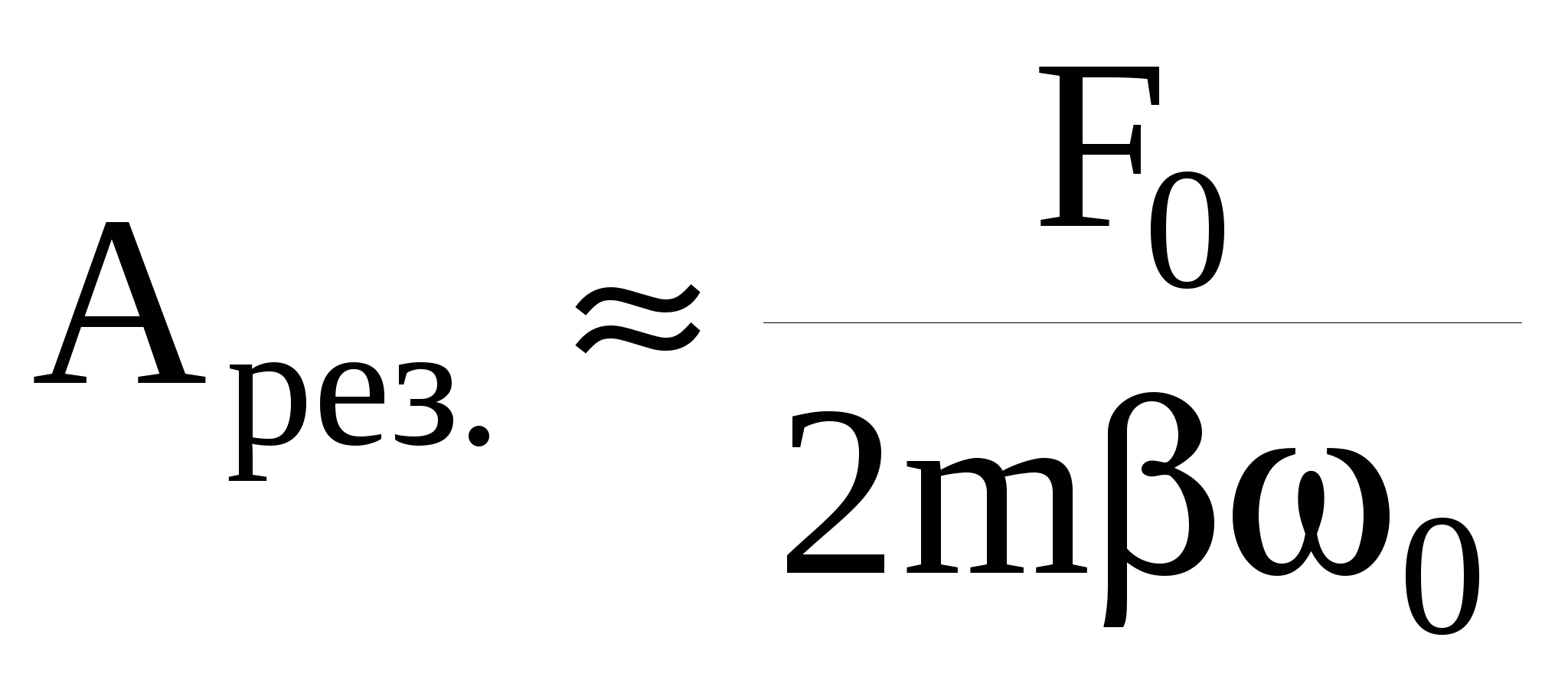 (37а) (37а)
При этом условии возьмем отношение резонансного смещения к статическому отклонению.
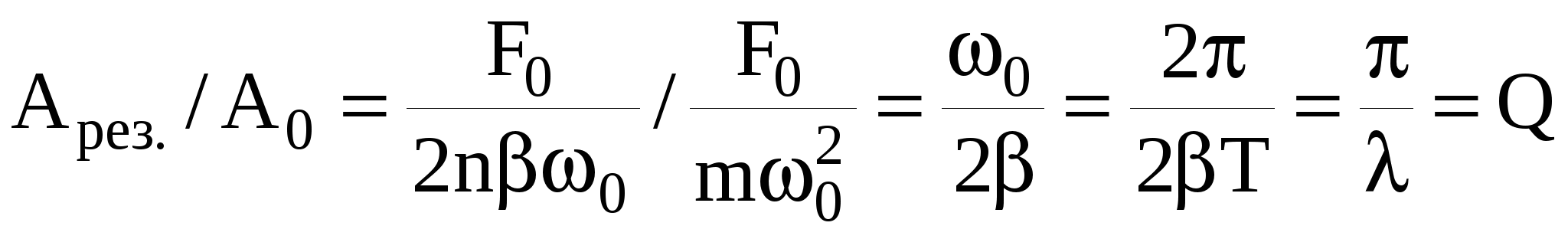 , ,
из которого видно, что относительное увеличение амплитуды колебаний при резонансе определяется добротностью колебательной системы. Здесь добротность является по сути коэффициентом усиления отклика 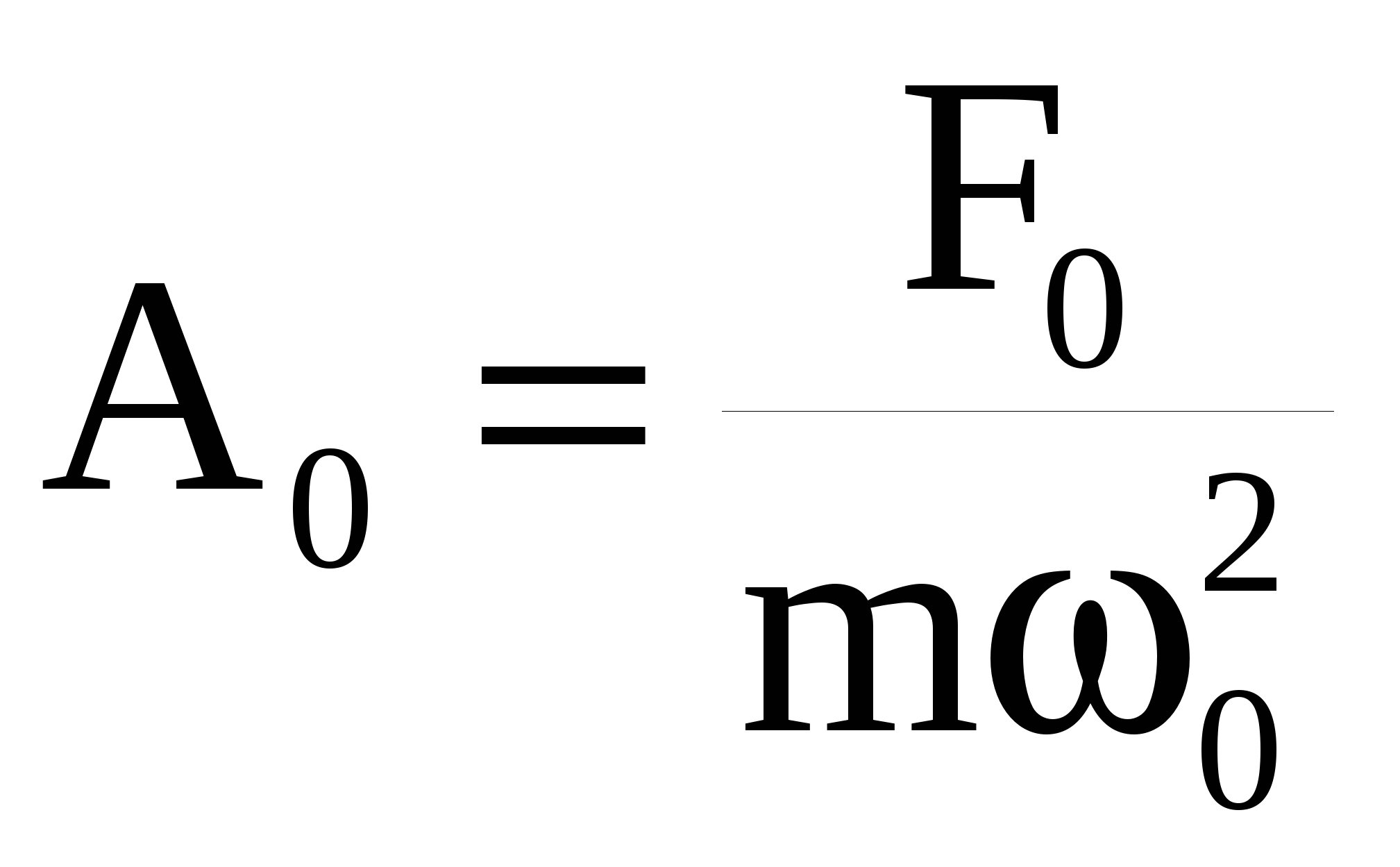 системы и при малом затухании может достигать больших значений. системы и при малом затухании может достигать больших значений.
Это обстоятельство обусловливает огромное значение явления резонанса в физике и технике. Его используют, если хотят усилить колебания, например, в акустике – для усиления звучания музыкальных инструментов, в радиотехнике – для выделения нужного сигнала из множества других, отличающихся по частоте. Если резонанс может привести к нежелательному росту колебаний, пользуются системой с малой добротностью.
СВЯЗАННЫЕ КОЛЕБАНИЯ
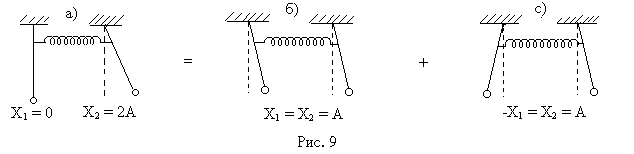
Источником внешней периодической силы может служить вторая колебательная система, упруго связанная с первой. Обе колебательные системы могут действовать одна на другую. Так, например, случай двух связанных маятников (рис. 9).
Система может совершать как синфазные (рис. 9б), так и противофазные (рис. 9с) колебания. Такие колебания называются нормальным типом или нормальной модой колебаний и характеризуются своей собственной нормальной частотой. При синфазных колебаниях смещения маятников во все моменты времени Х1 = Х2, а частота ω1 точно такая же, как частота отдельно взятого маятника 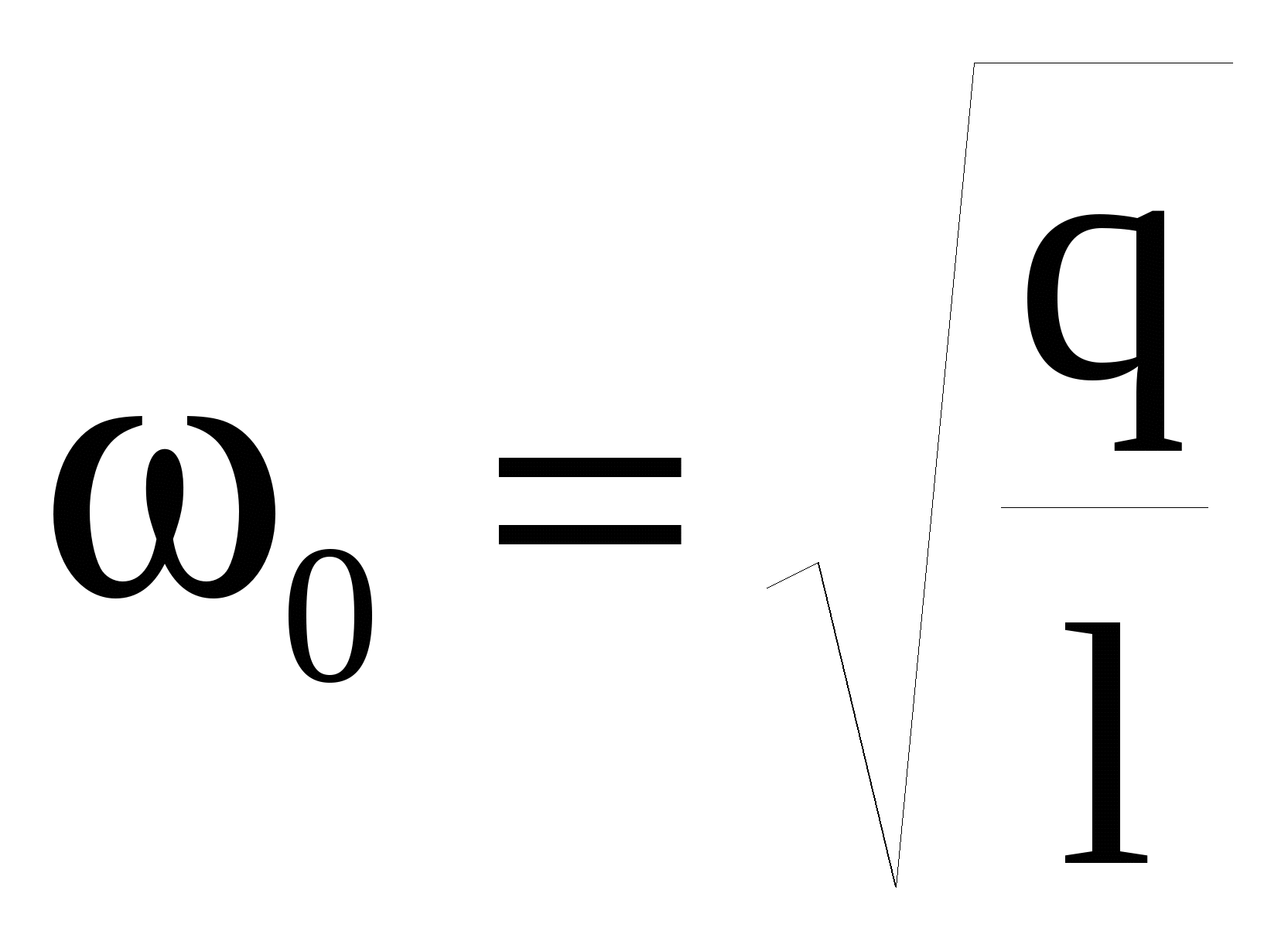 . Это объясняется тем, что легкая пружина находится в свободном состоянии и не оказывает никакого влияния на движение. При противофазных колебаниях во все моменты времени – Х1 = Х2. Частота таких колебаний больше и равна . Это объясняется тем, что легкая пружина находится в свободном состоянии и не оказывает никакого влияния на движение. При противофазных колебаниях во все моменты времени – Х1 = Х2. Частота таких колебаний больше и равна 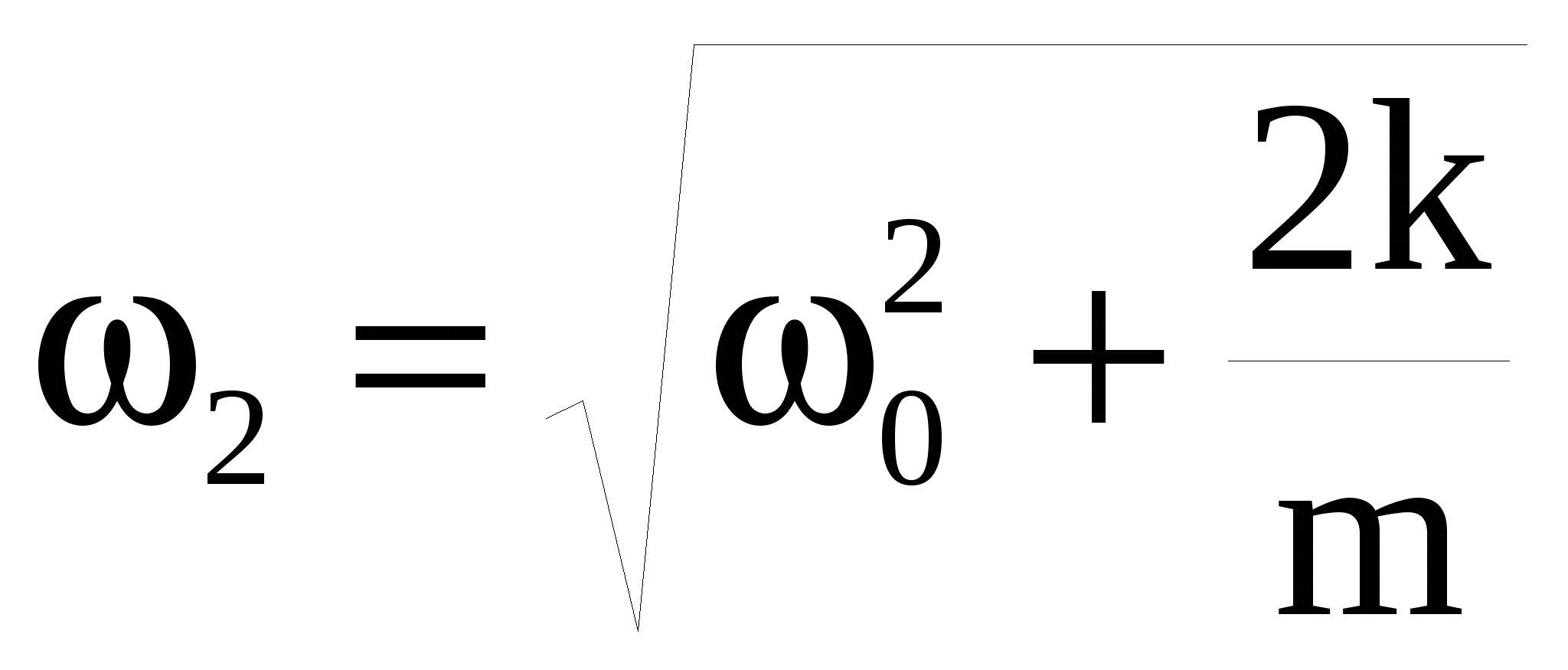 , так как пружина, обладающая жесткостью k и осуществляющая связь, все время находится то в растянутом, то в сжатом состоянии. , так как пружина, обладающая жесткостью k и осуществляющая связь, все время находится то в растянутом, то в сжатом состоянии.
Любое состояние нашей связанной системы, в том числе и начальное смещение Х (рис. 9а), можно представить в виде суперпозиции двух нормальных мод:
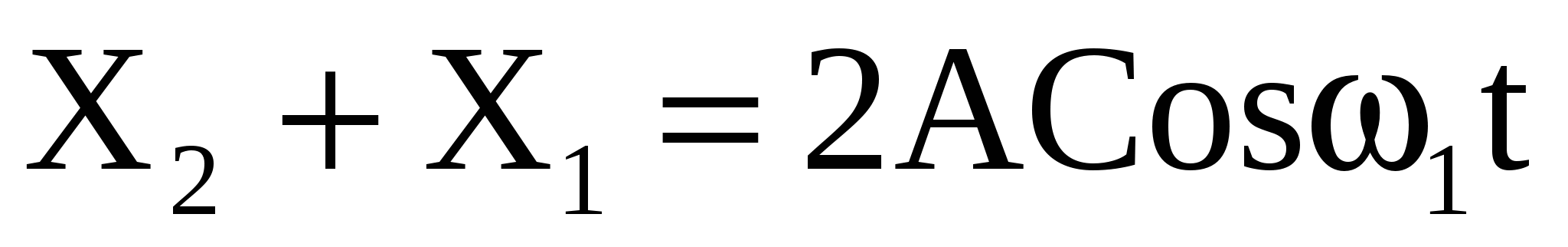 и и 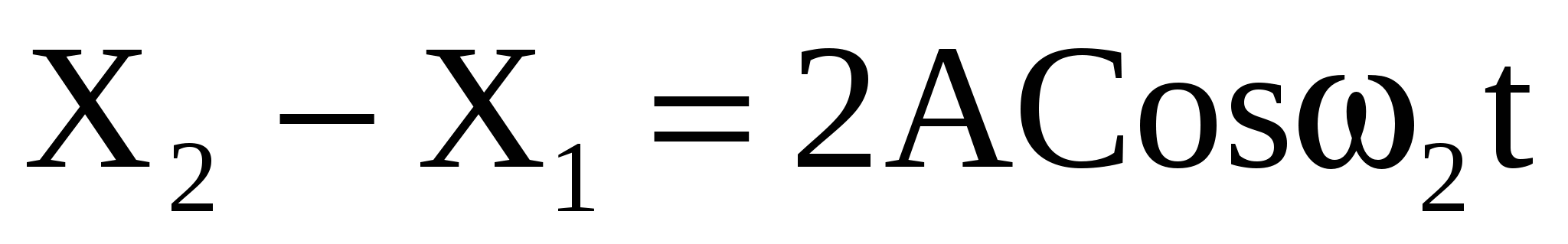 . .
Если привести систему в движение из начального состояния Х1 = 0, 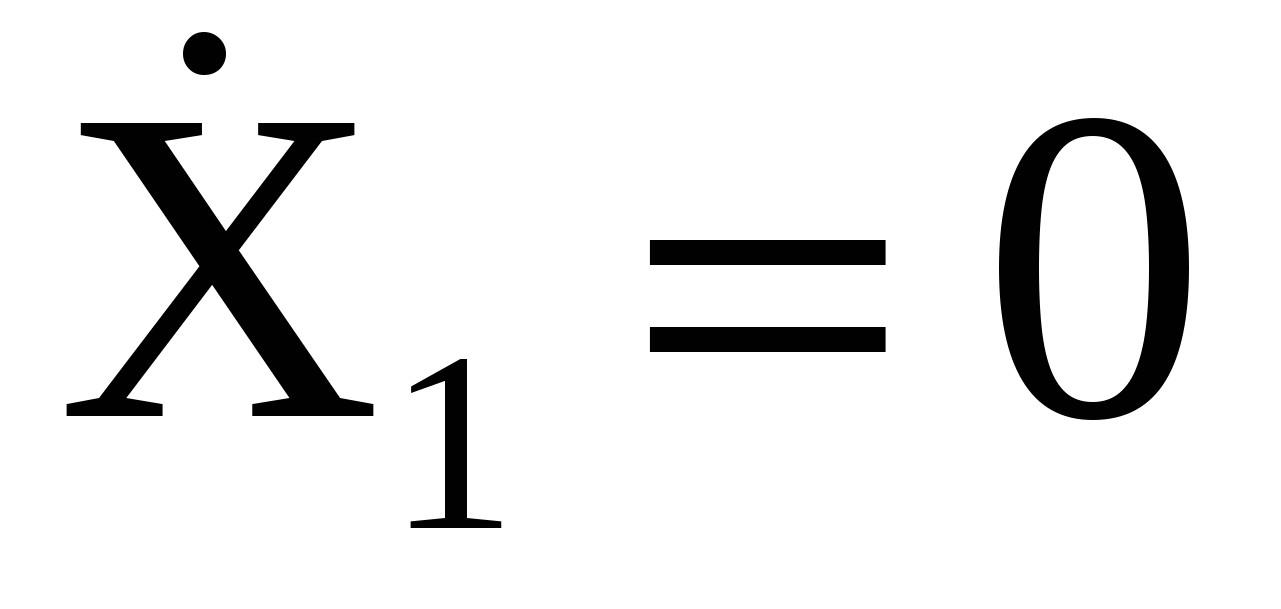 , Х2 = 2А, , Х2 = 2А, 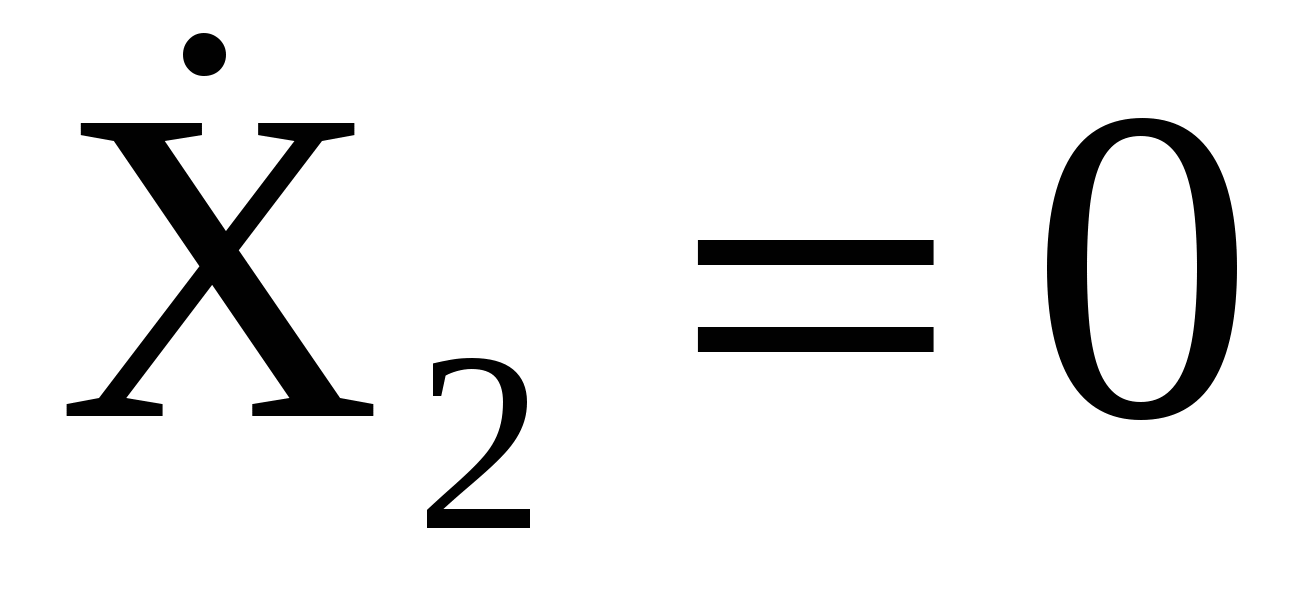 , ,
то смещения маятников будут описываться выражениями:
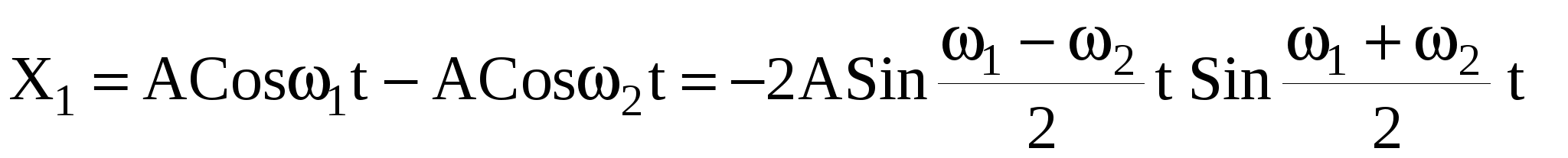 , ,
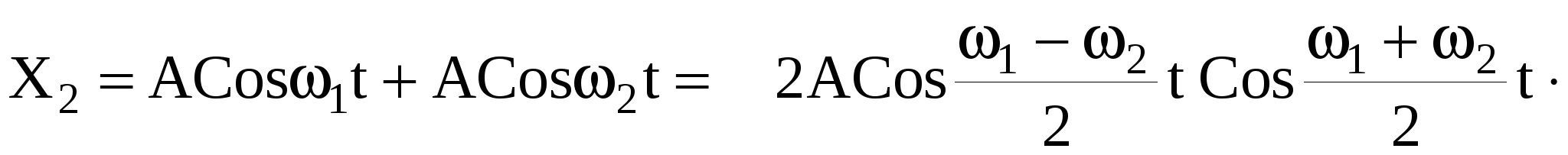 (38) (38)
На рис. 10 представлено изменение смещения отдельных маятников во времени.
Ч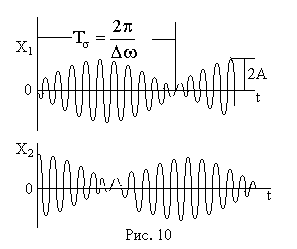
астота колебаний маятников равна средней частоте двух нормальных мод
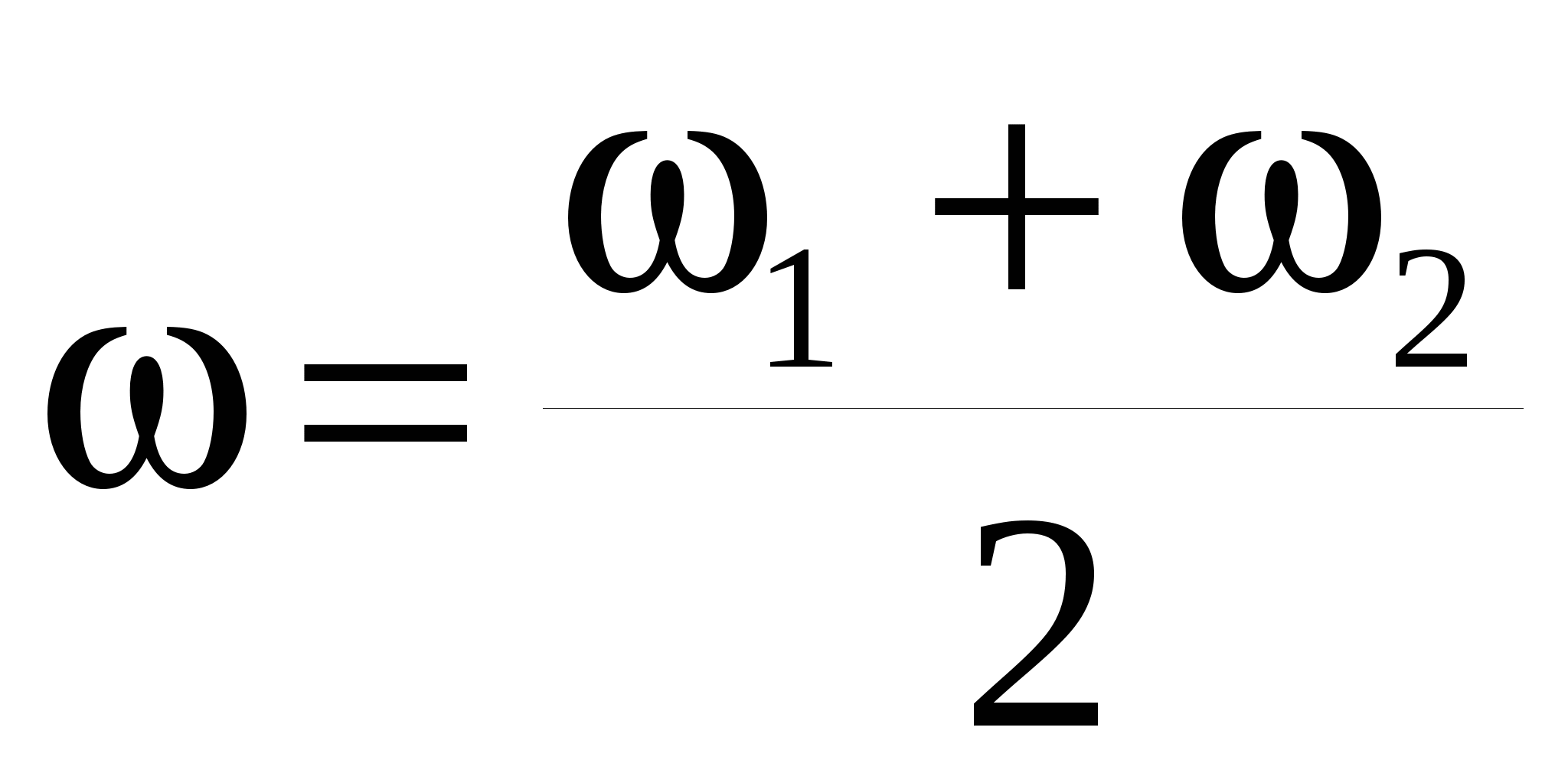 (39) (39)
а их амплитуда изменяется по закону синуса или конуса с меньшей частотой, равной половине разности частоты нормальных мод
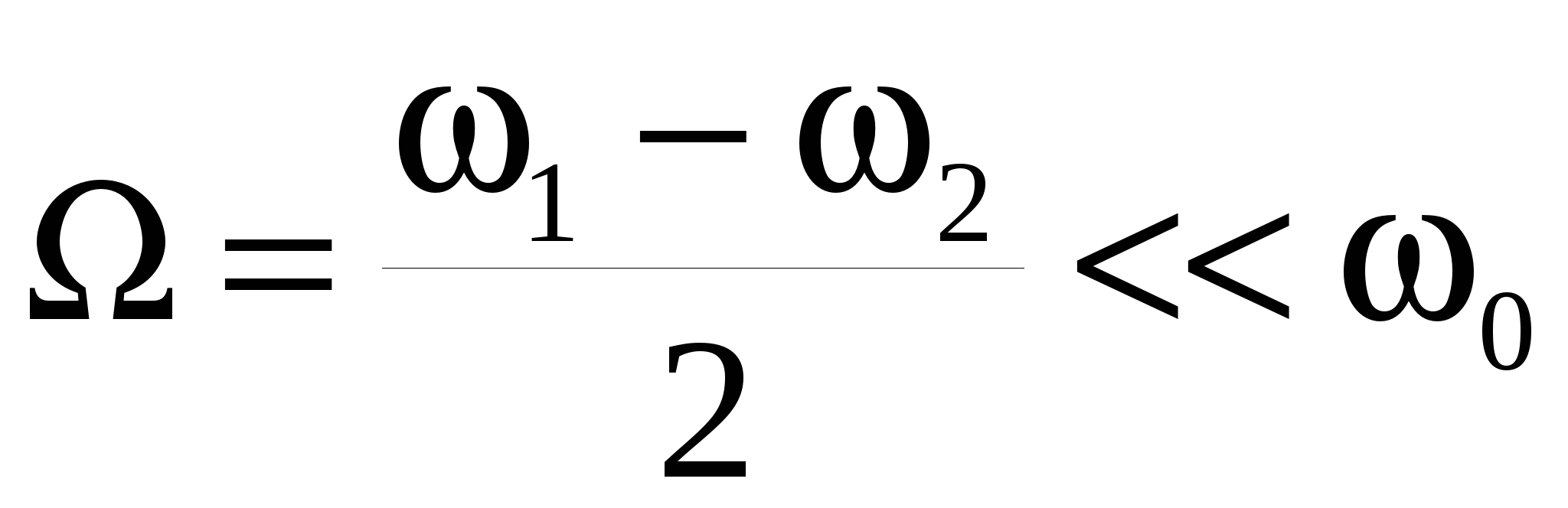 . (40) . (40)
Медленное изменение амплитуды с частотой, равной половине разности частот нормальных мод, называется “биениями” двух колебаний с почти одинаковыми частотами. Частота “биений” равна разности ω1 –ω2 частот, (а не половине этой разности), поскольку максимум амплитуды 2А достигается дважды за период, соответствующий частоте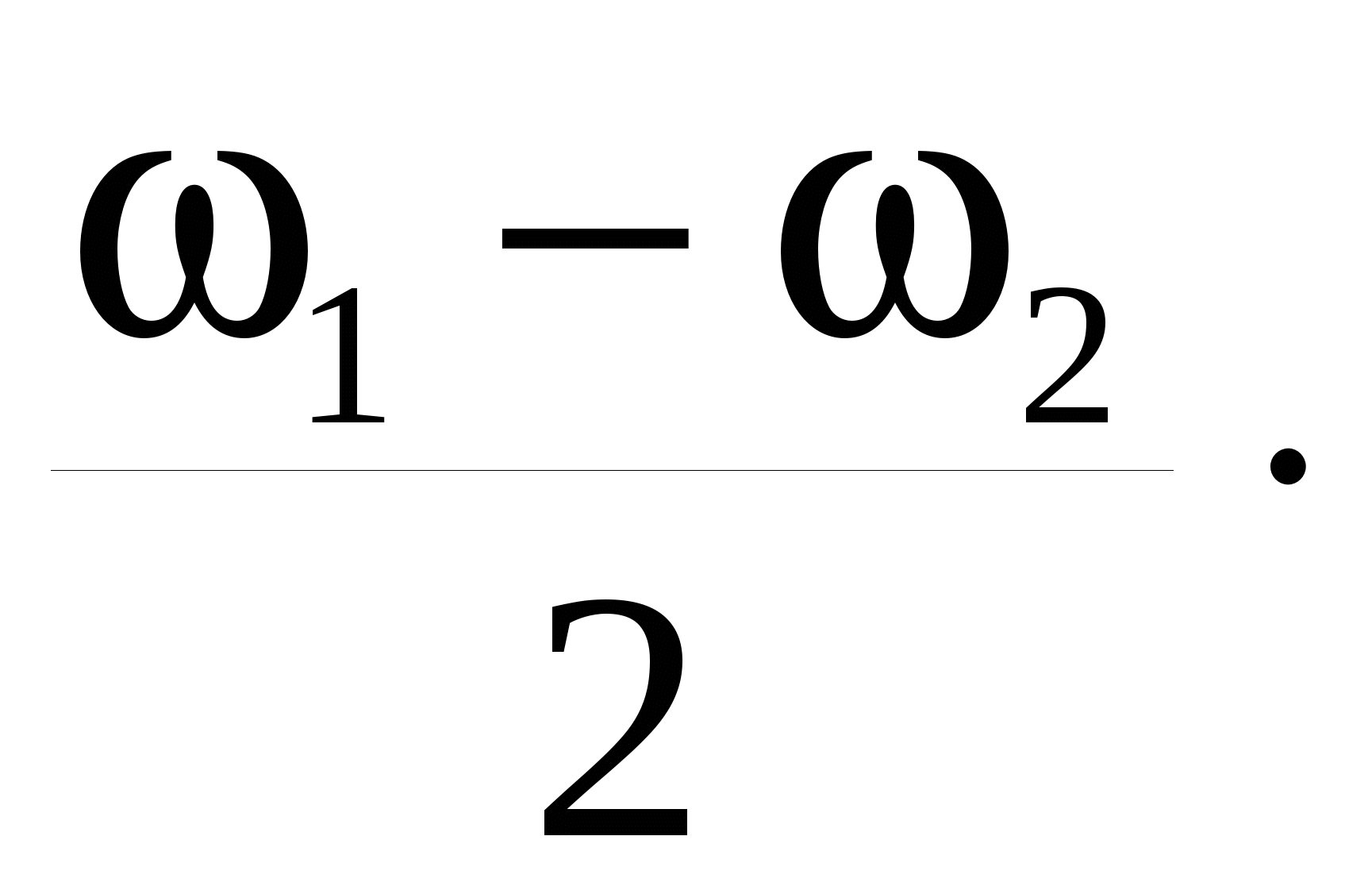
Отсюда период биений оказывается равным
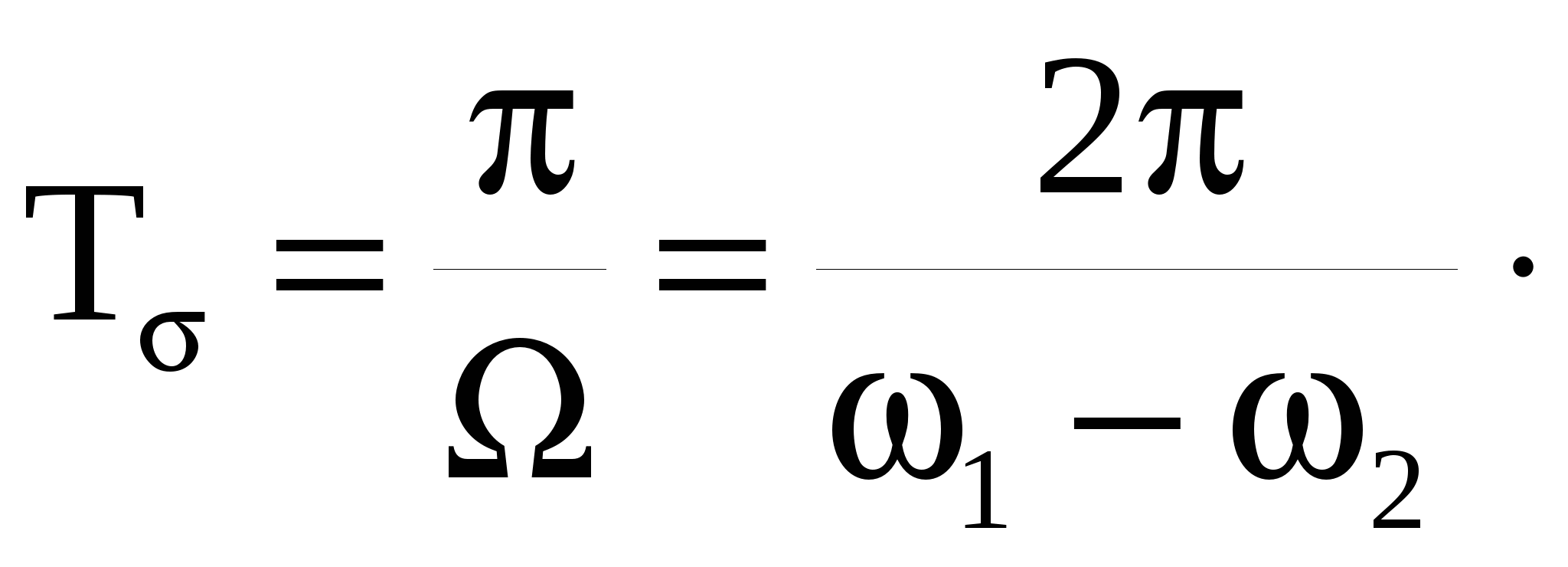 (41) (41)
При биениях между маятниками происходит обмен энергией. Однако полный обмен энергией возможен только тогда, когда обе массы одинаковы и отношение (ω1+ω2 / ω1-ω2) равно целому числу. Необходимо отметить один важный момент: хотя отдельные маятники могут обмениваться энергией, обмен энергией между нормальными модами отсутствует.
Наличие таких колеблющихся систем, которые взаимодействуют между собой и способны передавать друг другу свою энергию, составляют основу волнового движения.
|
|
|
 Скачать 2.69 Mb.
Скачать 2.69 Mb.

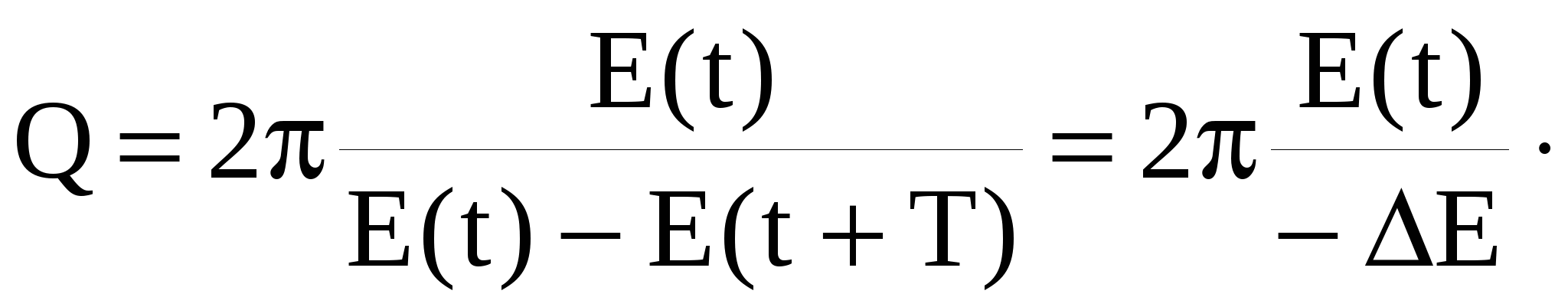 (29)
(29)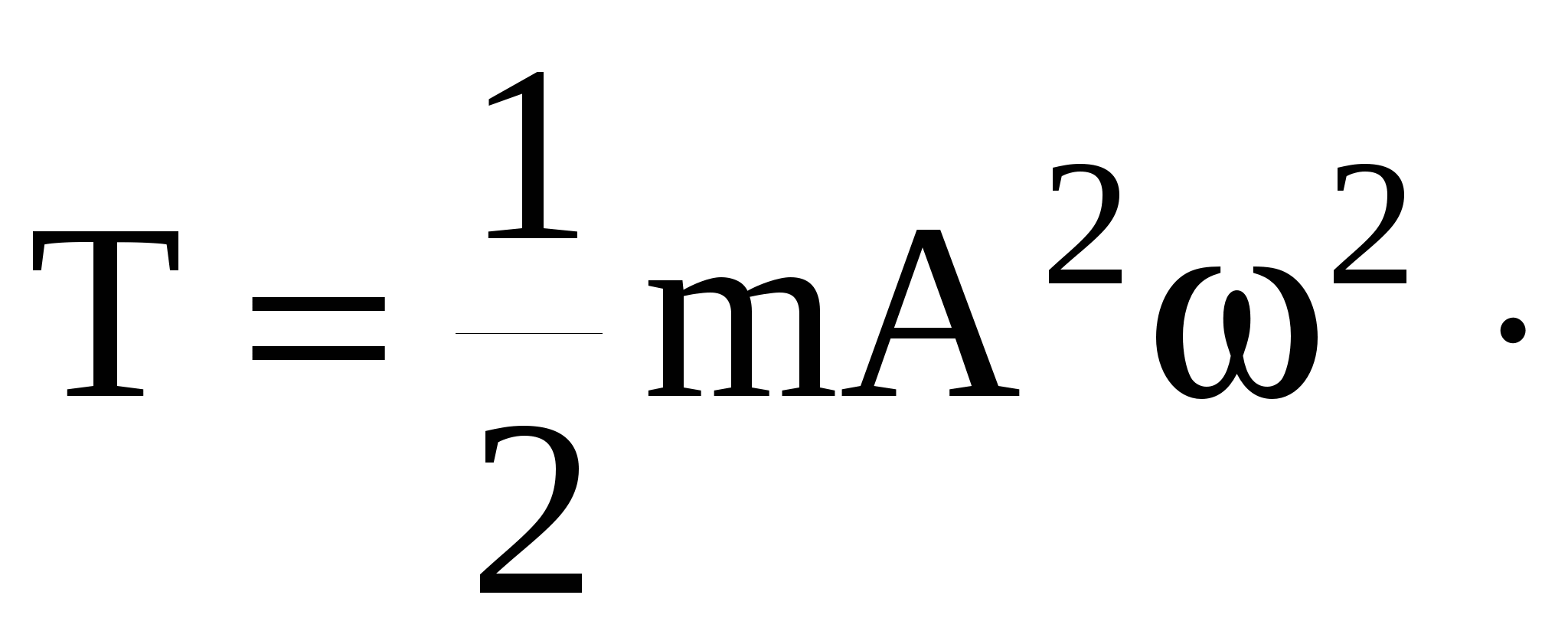 (30)
(30) 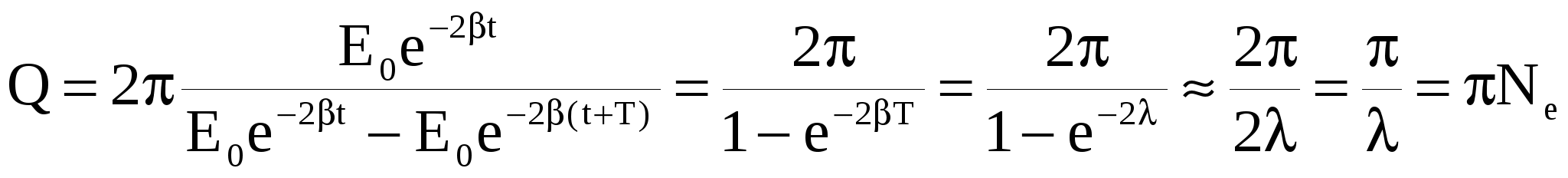 . (32)
. (32)




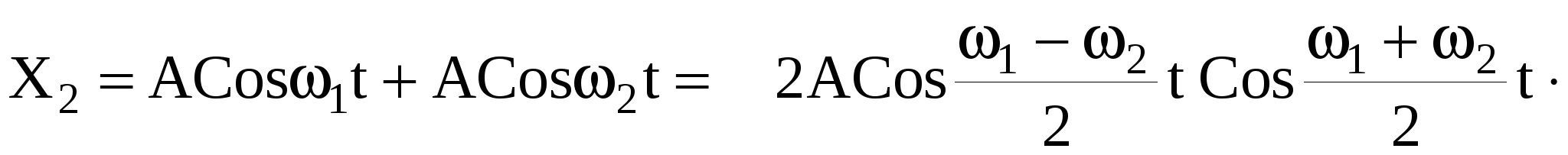 (38)
(38)
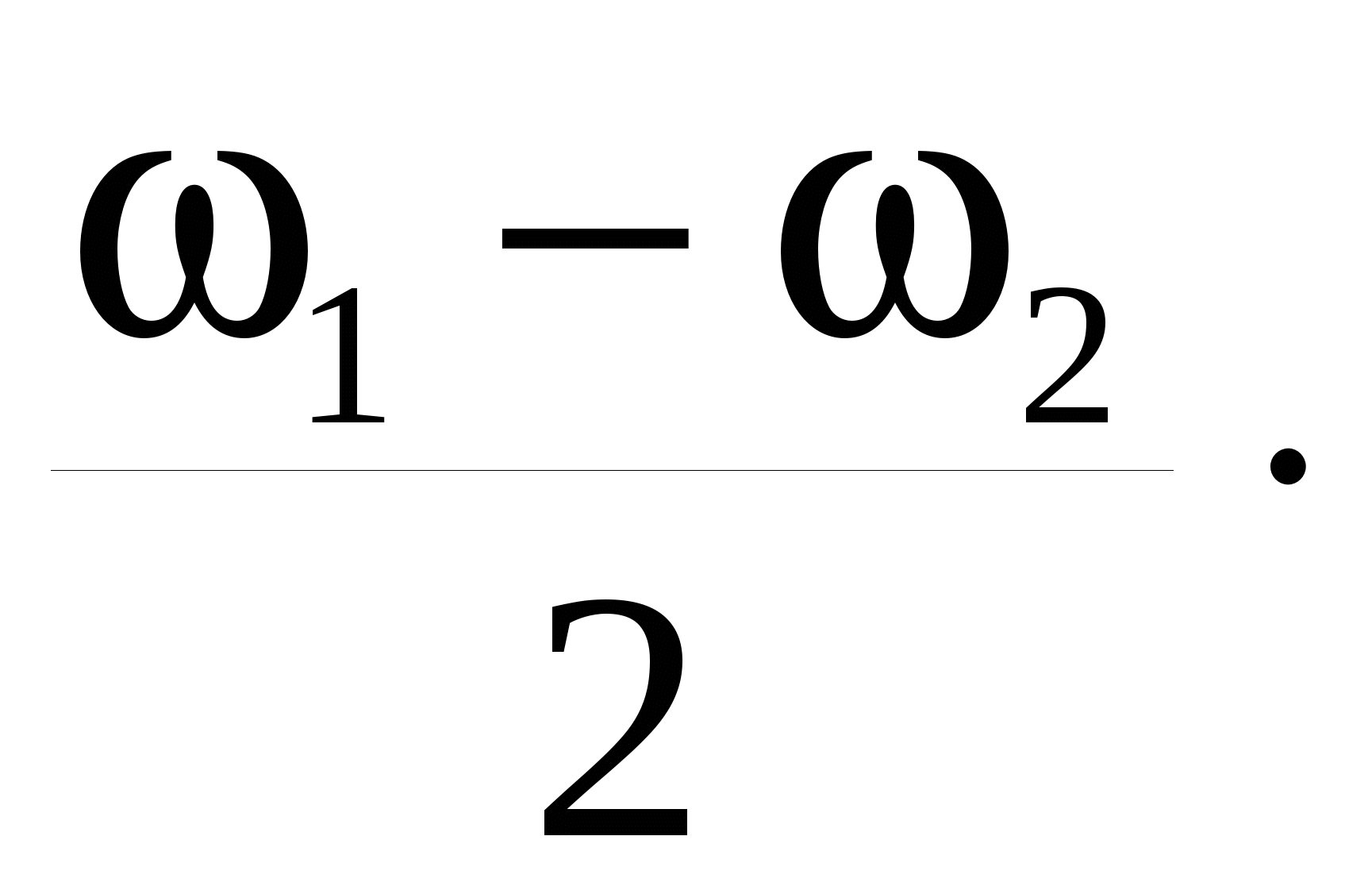
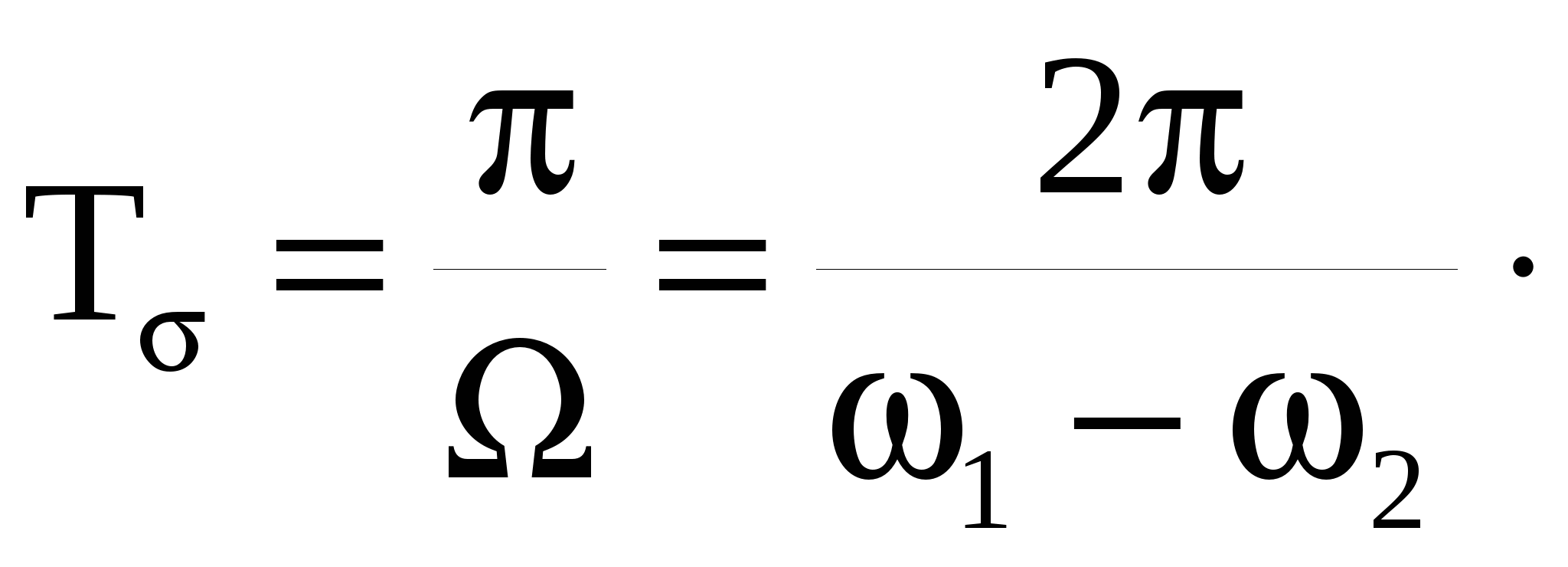 (41)
(41)