Лабораторная работа 110 введение

• Название: Лабораторная работа 110 введение
• Анкор: LR110.doc
• Дата: 20.05.2017
• Размер: 2.69 Mb.
• Имя файла: LR110.doc
• Тип: Лабораторная работа; #8019
• страница: 3 из 4

ВОЛНЫ

Колеблющееся материальное тело, помещенное в упругую среду, увлекает за собой и приводит в колебательное движение прилегающие к нему частицы среды. Благодаря наличию упругих связей между частицами колебания распространяются с характерной для данной среды скоростью по всей среде.

Процесс распространения колебаний в упругой среде называется волной. Различают два основных типа волн: продольные и поперечные. В продольных волнах частицы среды колеблются вдоль направления распространения волны, а в поперечных – перпендикулярно к направлению распространения волны. Не во всякой упругой среде возможно распространение поперечной волны. Поперечная упругая волна возможна лишь в таких средах, в которых имеет место упругая деформация сдвига. Например, в газах и жидкостях распространяются только продольные упругие волны (звук).

Геометрическое место точек среды, до которых к данному моменту времени дошло колебание, называется фронтом волны. Фронт волны отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникали. В зависимости от формы фронта различают волны плоские, сферические, цилиндрические и т.д.
Уравнение плоской волны, распространяющейся без потерь в однородной среде, имеет вид

, (42)

где ξ(Х,t) – смещение частиц среды с координатой Х от положения равновесия в момент времени t, А – амплитуда, - фаза волны, - круговая частота колебания частиц среды, v – скорость распространения волны.

Длиной волны λ называется расстояние между точками, колеблющимися с разностью фаз 2π, другими словами, длиной волны называется путь, проходимый любой фазой волны за один период колебаний:

λ = vT, (43)

фазовая скорость, т.е. скорость распространения данной фазы:

λ / Т (44)

Волновое число – число длин волн, укладывающихся на длине 2π единиц:

k = ω / v = 2π / λ. (45)

Подставляя эти обозначения в (42), уравнение плоской бегущей монохроматической волны можно представить в виде

(4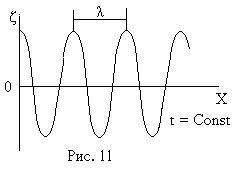6)

О
тметим, что уравнение волны (46) обнаруживает двойную периодичность по координате и времени. Действительно, фазы колебаний совпадают при изменении координаты на λ и при

изменении времени на Т (период). Поэтому изобразить графически волну на плоскости нельзя. Часто фиксируют время t и на графике представляют зависимость смещения ξ от координаты Х, т.е. мгновенное распределение смещений частиц среды вдоль направления распространения волны (рис.11). Разность фаз Δφ колебаний точек среды зависит от расстояния ΔХ =Х₂ – Х₁ между этими точками

(47)

Если волна распространяется противоположно направлению Х, то уравнение обратной волны запишется в виде:

ξ (Х,t) = АСos(ωt + kX). (48)

СТОЯЧИЕ ВОЛНЫ – это результат особого вида интерференции волн. Они образуются при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.

Уравнения двух плоских волн, распространяющихся вдоль оси Х в противоположных направлениях, имеют вид:

ξ₁ =АСos(ωt – kX)

ξ₂ = AСos(ωt + kX). (49)

Складывая эти уравнения по формуле суммы косинусов и учитывая, что k = 2π / λ, получим уравнение стоячей волны

. (50)

Множитель Сos ωt показывает, что в точках среды возникает колебание той же частоты ω с амплитудой , зависящей от координаты Х рассматриваемой точки. В точках среды, где

, (51)

амплитуда колебаний достигает максимального значения, равного 2А. Эти точки называются пучностями. Из выражения (51) можно найти координаты пучностей:

(52)

В точках, где , (53)

амплитуда колебаний обращается в нуль. Эти точки называются узлами. Координаты узлов

. (5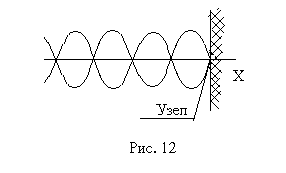4)

Р
асстояния между соседними пучностями и соседними узлами одинаковы и равны λ/2. Расстояние между узлом и соседней пучностью равно λ / 4. При переходе через узел множитель меняет знак, поэтому фазы колебаний по разные стороны от узла отличаются на π, т.е. точки, лежащие по разные стороны от узла, колеблются в противофазе. Точки, заключенные между двумя соседними узлами, колеблются с разными амплитудами, но с одинаковыми фазами.

Распределение узлов и пучностей в стоячей волне зависит от условий, имеющих место на границе раздела двух сред, от которой происходит отражение. Если отражение волны происходит от среды более плотной, то фаза колебаний в месте отражения волны меняется на противоположную или, как говорят, теряется половина волны. Поэтому, в результате сложения колебаний противоположных направлений смещение на границе равно нулю, т.е. имеет место узел (рис. 12). При отражении волны от границы менее плотной среды фаза колебаний в месте отражения остается без изменения и у границы складываются колебания с одинаковыми фазами – получается пучность.

В стоячей волне нет перемещения фаз, нет распространения волны, нет переноса энергии, с чем и связано название такого типа волн.


ЛАБОРАТОРНАЯ РАБОТА 110