Лабораторная работа 110 введение

• Название: Лабораторная работа 110 введение
• Анкор: LR110.doc
• Дата: 20.05.2017
• Размер: 2.69 Mb.
• Имя файла: LR110.doc
• Тип: Лабораторная работа; #8019
• страница: 4 из 4

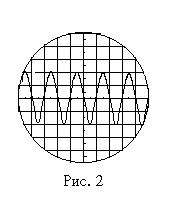
ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ЗАТУХАНИЯ КАМЕРТОНА

Цель работы: изучить затухающие колебания и определить основные пареметры затухания камертона.

Приборы и принадлежности: камертон, укрепленный неподвижно на подставке, индикатор колебаний – электронный осциллограф, секундомер, резиновый молоток, поролоновый демпфер.

Описание метода и приборов.

В данной работе предлагается по времени относительного изменения амплитуды колебаний камертона известной частоты определить основные характеристики его затухания: коэффициент затухания β, время релаксации τ, логарифмический декремент затухания λ и добротность Q.

Степень убывания амплитуды затухающих колебаний определяется коэффициентом затухания β

, (1)

где А₀ – амплитуда колебаний в начале отсчета времени при t = 0.

Время релаксации τ характеризует время жизни колебаний. За время

(2)

амплитуда уменьшается в е ≈ 2,72 раз.

Скорость уменьшения амплитуды характеризуется логарифмическим декрементом затухания

λ = βΤ, (3)

где Т – период колебаний.

Если известна частота колебаний камертона ν, то период колебаний

. (4)

Добротность колебательной системы характеризует скорость уменьшения энергии и может быть выражена формулой

. (5)

Если решить уравнение (1) относительно β, то получится

. (6)

Пусть амплитуда колебаний за время t убывает в два раза. Тогда

. (6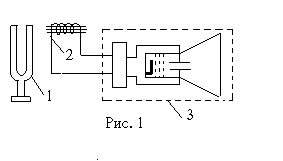а)

Значит для определения β достаточно измерить время, в течение которого амплитуда колебаний убывает вдвое.

Измерение амплитуд колебаний камертона в данной работе производится с помощью электронно – лучевого индикатора (осциллографа). На рис. 1 приведена схема установки, где приняты следующие условные обозначения: 1 – камертон, 2 – датчик, 3 – осциллограф. Датчик представляет собой катушку с большим числом витков, которая надета на незамкнутый сердечник из трансформаторного железа. Концы обмотки подключаются на вход усилителя осциллографа.

Ветви камертона слабо намагничены. Если его заставить колебаться, то магнитный поток, пронизывающий датчик, становится переменным, вследствие чего в обмотках датчика возникает ЭДС индукции, частота и амплитуда которой соответствует частоте и амплитуде колебаний камертона. Переменное синусоидальное напряжение увеличивается усилителем осциллографа и подается на вертикально отклоняющиеся пластины электронно – лучевой трубки. Особенностью усилителя является его линейность, т.е. изменение амплитуды ЭДС передается без искажения. Таким образом, на экране осциллографа наблюдаются затухающие колебания, соответствующие колебаниям камертона.

Порядок выполнения работы

1. 
   Включить осциллограф в сеть (220 В). Через 1 – 2 минуты на экране появится горизонтальная светлая полоса, которая должна проходить через середину сетки, стоящей перед экраном.
   

П р и м е ч а н и е: если этого не будет, то необходимо обратиться за помощью к лаборанту или преподавателю.

2. 
   Коротк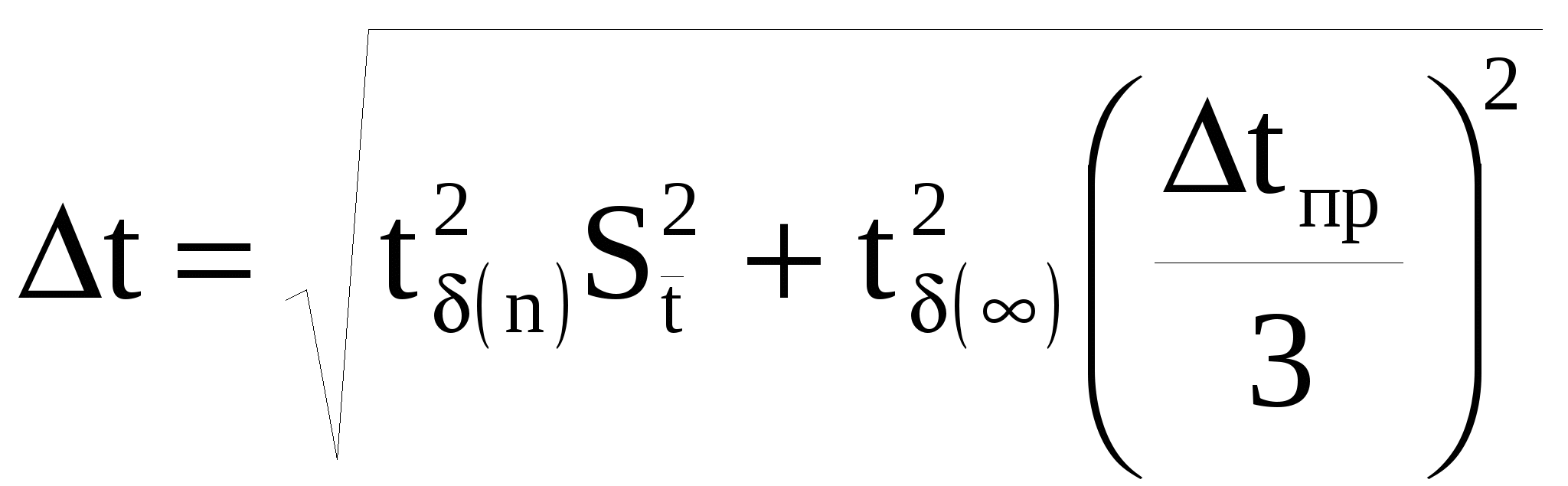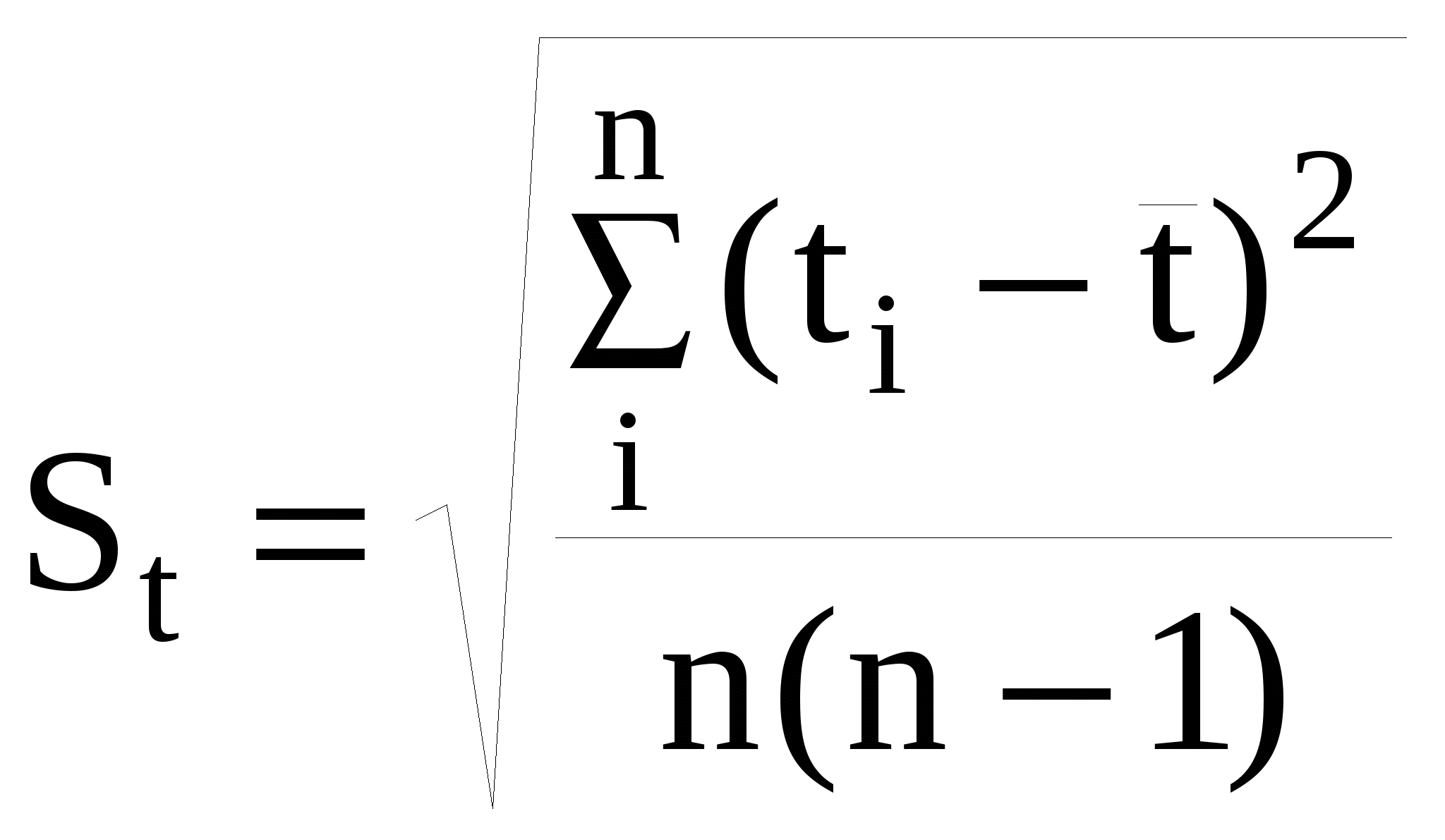им ударом резинового молотка привести камертон в колебание. На рис. 2 показана картина, которая наблюдается после удара. До удара по камертону на экране осциллографа должна наблюдаться горизонтальная прямая.
   

3. 
   И
   змерить время затухания колебаний t. Для этого в момент, когда полный размах амплитуды колебаний на экране осциллографа достигнет четырех клеток, запустить секундомер. Продолжая наблюдать за амплитудой, остановить его в тот момент, когда амплитуда колебаний станет равной половине начальной. Опыт повторить 3 раза и вычислить среднее время .
   

4. 
   Определить период камертона по формуле (4). Частота камертона ν приведена на установке.
   
5. 
   Используя среднее значение времени затухания и период колебаний Т, по формулам (6а), (2), (3), и (5) вычислить параметры затухания камертона . Результаты измерений и расчетов занести в таблицу.
   
6. 
   Оценить погрешность измерения и , приняв за основную погрешность опыта ошибку измерения времени ∆t, по формулам
   

, (7)
, (8)
Здесь - средняя квадратичная ошибка измерения времени; t_δ(n) – коэффициент Стьюдента для числа измерений n = 3 при доверительной вероятности δ = 0,95 (находится по таблице коэффициентов Стьюдента); - то же для бесконечного числа измерений; ∆t_пр – приборная погрешность секундомера, принимаемая за 0,1 с.

4. 
   Результаты измерения t и β представить в виде
   

при, n = 3, δ = 0,95,

при n = 3, δ = 0,95

i	2A0, мм	2А(t), мм	ti, с		,с			, с
1
2
3

Упражнение. Определение относительного изменения добротности камертона при возрастании сопротивления среды.

В качестве демпфера (успокоителя) между ветвями камертона поместить поролоновую прокладку. Затухание камертона при этом заметно возрастает. В предположении, что частота колебаний камертона сильно не изменилась, т.е. сохранилось условие β<<ω₀, выполнить пункт 3 предыдущего задания и по результатам новых измерений рассчитать относительное изменение добротности по формуле



Результаты новых измерений времени затухания , добротности и γ записать в таблицу.

Контрольные вопросы

1. 
   Какие колебания называются гармоническими?
   
2. 
   Дайте определение амплитуды, фазы, периода, частоты, циклической частоты колебания.
   
3. 
   Какие колебания называются затухающими? Являются ли затухающие колебания гармоническими?
   
4. 
   Запишите дифференциальное уравнение затухающих колебаний и его решение.
   
5. 
   Почему частота затухающих колебаний меньше частоты собственных колебаний системы? При каких условиях наблюдается апериодическое движение?
   
6. 
   Что такое коэффициент затухания? Время релаксации? Декремент затухания? Логарифмический декремент затухания? Добротность колебательной системы? В чем заключается физический смысл этих величин?
   

Литература
[1, с. 204];[2, с. 229];[3, с. 38]

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. 
   Савельев И.В. Курс общей физики. Т.I. М.: Наука, 1982.
   
2. 
   Трофимова Г.И. Курс физики, М.: Высшая школа, 1990.
   
3. 
   Пейн Г.Я. Физика колебаний и волн. М.: Мир, 1979.
   
4. 
   Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 1989.