Математическая обработка результатов измерений Вопросы
 Скачать 0.71 Mb.
|
|
Математическая обработка результатов измерений Вопросы 1. Прямые измерения с многократными наблюдениями 2. Косвенные измерения 3. Обработка результатов нескольких серий измерений 4. Оценка неопределенности измерений Вопрос 1. Прямые измерения с многократными наблюдениями Обработка данных, полученных в ходе эксперимента, проводится с целью определения результата измерения и оценки его точности. Выбор метода обработки зависит от числа наблюдений (однократные или многократные) и вида измерений (прямые, косвенные, совокупные или совместные). Соответственно, для каждого вида измерений существует свой метод обработки данных. Правила обработки результатов прямых измерений с многократными наблюдениями регламентирует ГОСТ 8.207–76. Он применим только для равноточных многократных измерений. Равноточными измерениями называется ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью Задача обработки результатов многократных измерений заключается в нахождении оценки измеряемой величины и доверительного интервала, в котором находится ее истинное значение. Исходной информацией для обработки является группа из nнезависимых результатов наблюдений случайной величины  , подчиняющейся нормальному распределению. Правила обработки результатов измерений с многократными наблюдениями учитывают следующие факторы: – обрабатывается ограниченная группа из nнаблюдений; – результаты наблюдений могут содержать систематическую погрешность; – в группе наблюдений могут встречаться грубые погрешности; – распределение случайных погрешностей может отличаться от нормального. Обработка результатов наблюдений проводится в следующей последовательности. 1. Исключить известные систематические погрешности из результатов наблюдений (введение поправки). 2. Исключить из результатов наблюдений результаты с грубыми погрешностями. Для этого может быть использован один из критериев, описанных в Теме 4. 3. Вычислить среднее арифметическое исправленных (после введения поправки) результатов наблюдений, принимаемое за результат измерения:  . (1)4. Вычислить оценку среднего квадратического отклонения результатов наблюдений 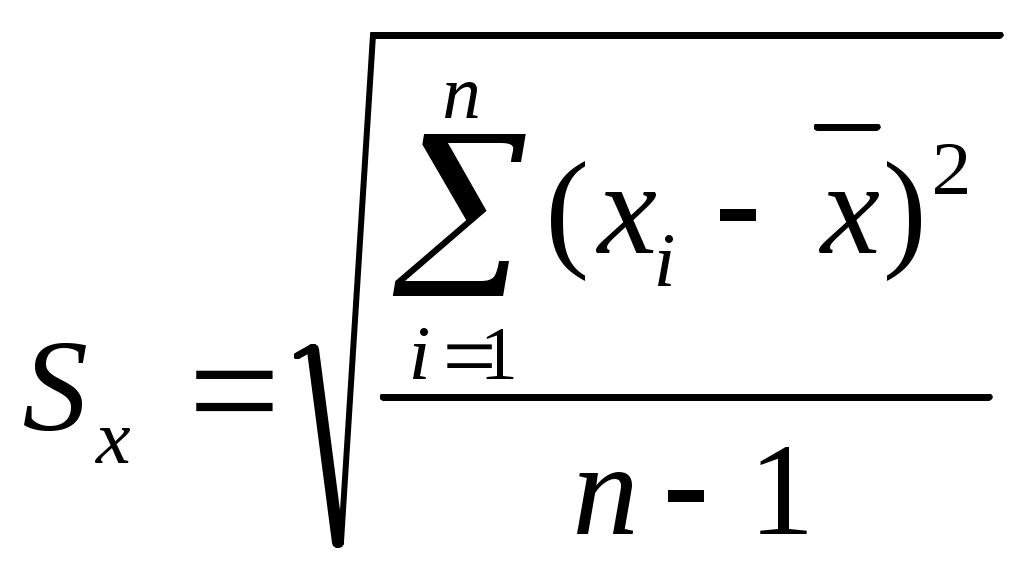 . (2)5. Вычислить оценку среднего квадратического отклонения результата измерения (среднего арифметического)  . (3)6. Проверить гипотезу нормального закона распределения результатов наблюдений. Приближенно о характере распределения можно судить по гистограмме, построенной по результатам наблюдений. Для этого их выстраивают в вариационный ряд в порядке возрастания. Затем ряд разбивают на оптимальное число  , как правило, одинаковых интервалов группирования длиной  .Оптимальное число интервалов должно находиться в пределах от  до  и быть нечетным. Далее определяют длину каждого интервала  ;  и т. д и подсчитывают число попаданий  (частоты) результатов измерений в каждый интервал группирования или вероятности попадания (частости)  . По полученным данным строят гистограмму, откладывая по оси ординат интервалы  . На каждом из них строят прямоугольник высотой или  . Соединив середины верхних оснований каждого столбца гистограммы, получают ломаную линию, которая называется полигон. Полигон отражает форму плотности кривой распределения вероятностей. По виду построенной гистограммы можно приблизительно оценить закон распределения вероятностей.Для оценки нормальности при числе наблюдений  могут быть применены строгие методы проверки гипотез с использованием специальных критериев (2 – Пирсона, 2 – Мозеса–Смирнова и др.).При  для проверки нормальности законов распределения применяют составной критерий, приведенный в ГОСТ 8.207–76.При числе наблюдений n 15 принадлежность их к нормальному распределению не проверяют, а доверительные границы случайной погрешности результата определяют лишь в том случае, если достоверно известно, что результаты наблюдений принадлежат нормальному закону. 7. Определить доверительные границы случайной погрешности результата измерения при заданной доверительной вероятности Р и п<20: =  , (4)где t – коэффициент Стьюдента. 8. Вычислить границы суммарной неисключенной систематической погрешности результата измерений, которая образуется из неисключенных систематических погрешностей метода, средств измерений, погрешностей поправок и др. При суммировании эти составляющие рассматриваются как случайные величины. При отсутствии данных о виде распределения неисключенных составляющих систематических погрешностей их распределение принимают за равномерное. При таком распределении неисключенных систематических погрешностей границы неисключенной систематической погрешности результата измерения  вычисляют по формуле  , (5)где  – коэффициент, определяемый принятой доверительной вероятностью и количеством неисключенных составляющих; m –количество неисключенных составляющих;  – границы i-й неисключенной составляющей систематической погрешности. При доверительной вероятности при Р = 0,95 =1,1; а при Р = 0,99 =1,4, если число суммируемых неисключенных систематических погрешностей более четырех ( ). Если же  , то коэффициент  определяют по графику, приведенному в ГОСТ 8.207–76. Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что и при вычислении границ случайной погрешности результата измерения. 9. Вычислить доверительные границы погрешности результата измерения. Анализ соотношения между неисключенной систематической погрешностью и случайной погрешностью показывает, что если  < 0,8, то неисключенной систематической погрешностью можно пренебречь и принять границы погрешности результата  равными  . Если  > 8, то случайной погрешностью можно пренебречь и принять границы погрешности результата равными  .Если оба неравенства не выполняются, вычисляют СКО результата как сумму неисключенной систематической погрешности 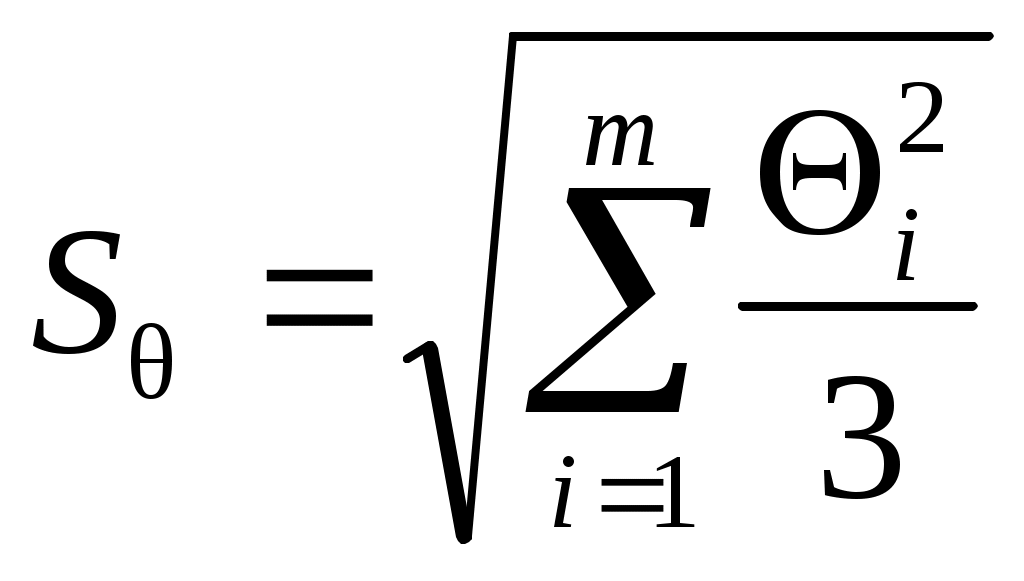 и случайной составляющей   , (6) . (7)Границы погрешности результата измерения в этом случае вычисляют по формуле  .(8)Коэффициент  вычисляют по эмпирической формуле . (9)10. Представить результат измерений. При симметричном доверительном интервале погрешности результат измерения представляют в форме  ,  , где  – результат измерения; – погрешность;  – доверительная вероятность.При отсутствии данных о видах функции распределения составляющих погрешности результата или при необходимости дальнейшей обработки, результат измерения представляют в форме , ,  , .Правила округления результатов измерений. Абсолютная погрешность результата измерения указывается двумя значащими цифрами, если первая из них 1 или 2, и одной, если первая цифра равна 3 или более. Значащей цифрой является любая цифра, кроме нуля, если он находится не в середине. Результат измерения округляется до того же десятичного знака, которым оканчивается округленное значение абсолютной погрешности. Если цифра старшего из отбрасываемых разрядов меньше 5, то оставшиеся цифры числа не изменяются. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю сохраняемую цифру увеличивают на единицу. Если отбрасываемая цифра равна 5, а следующие за ней неизвестны или ноль, то последнюю сохраняемую цифру числа не изменяют, если она четная и увеличивают на единицу, если она нечетная. Округление производят лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками. Вопрос 2. Косвенные измерения Косвенные измерения – это измерения, при которых искомое значение  находят на основании известной зависимости , (10)где   – значения, полученные при прямых измерениях. По виду функциональной зависимости делятся на две основные группы – линейные и нелинейные. Линейная зависимость – простейшая форма связи между измеряемой величиной и аргументами. Она может быть записана в виде  , (11)где  – коэффициент  -го аргумента; m – число аргументов.Порядок обработки результатов косвенных измерений дан в МИ 2083–90 и МИ 1730–87. 1. Результат косвенного измерения определяют по формуле , (12)где  – оценка результата измерения i-го аргумента, полученная путем обработки многократных прямых измерений.2. При отсутствии корреляционной связи между аргументами стандартное отклонение результата косвенного измерения  равно , (13)где – коэффициент -го аргумента; – стандартное отклонение результата измерения i-го аргумента. При наличии корреляционной связи между аргументами, которая возникает чаще всего в тех случаях, когда их измерения проводятся одновременно и подвергаются одинаковому влиянию внешних условий, необходимо учесть степень их корреляции через соответствующийкоэффициент.3. При большом числе измерений n 25–30 доверительные границы случайной погрешности  находят , (14)где  – квантиль функции нормированного нормального распределения при вероятности  , – стандартное отклонение результата косвенного измерения.При меньшем числе измерений используют распределение Стьюдента 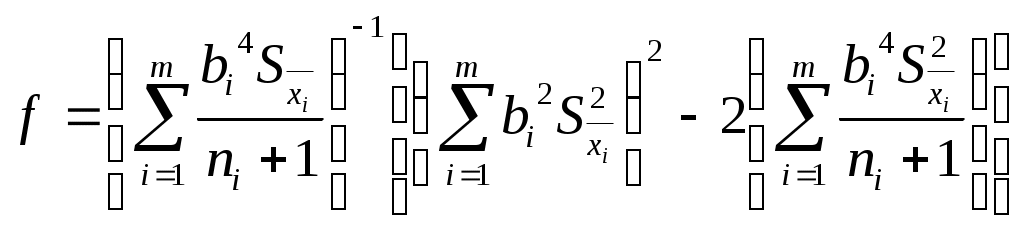 , (15)где  – коэффициент Стьюдента, – стандартное отклонение результата косвенного измерения.Коэффициент Стьюдента находят по доверительной вероятности Р и эффективному числу степеней свободы  , которое рассчитывают по формуле  , (16)где  – число измерений при определении -го аргумента.4. Доверительные границы неисключенной систематической погрешности результата линейного косвенного измерения  , в случае, если неисключенные систематические погрешности аргументов заданы границами ,вычисляют по формуле , (17)где – поправочный коэффициент, определяемый принятой доверительной вероятностью и числом составляющих . Его значения приведены в табл. 1. Таблица 1 Значения коэффициентов при
Если число суммируемых слагаемых , то значение коэффициента определяют по табл. 2. Под  здесь понимают отношение наибольшей длины интервала  одного из слагаемых к длине  остальных.Таблица 2 Значения коэффициента при  ,  , 
Если границы неисключенных систематических погрешностей результатов измерений аргументов заданы их доверительными границами  , соответствующими вероятностям  , то границу  определяют по формуле . (18)Коэффициенты  определяются так же, как поправочный коэффициент .5. Суммарную погрешность результата косвенного измерения оценивают на основе композиции распределений случайных и систематических погрешностей. Если  < 0,8 , то  , (19)  8, то  , (20) > 8, то  , (21)где  – коэффициент, который находят по табл. 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
