Математическая обработка результатов измерений Вопросы
 Скачать 0.71 Mb.
|
Таблица 3Зависимость  от отношения  при различной доверительной вероятности
6. Представляют результат аналогично прямым многократным измерениям. Для обработки результатов косвенных измерений при нелинейной зависимости между аргументами и некоррелированными погрешностями используется метод линеаризации. Он состоит в том, что нелинейная функция, связывающая величину с аргументами, разлагается в ряд Тейлора  , (22)где  – первая частная производная от функции  по аргументу  , вычисленная в точках  ;  – отклонение результата измерения аргумента от его среднего арифметического;  – остаточный член. Остаточным членом пренебрегают. Оценку результата измерения  производят по формуле  . (23)Погрешности результата косвенного измерения при нелинейной зависимости аргументов определяют по формулам (3.74–3.83), подставляя вместо   .Вопрос 3. Обработка результатов нескольких серий измерений Иногда многократные измерения одной и той же величины постоянного размера проводятся в несколько этапов, разными людьми, в различных условиях, в разных местах, в разное время. Результат определяется несколькими сериями полученных значений. Серии называются однородными, если состоят из значений, подчиняющихся одному и тому же закону распределения вероятностей. В противном случае они являются неоднородными. Проверка однородности является обязательной при выборе способа совместной обработки результатов нескольких серий измерений. Такая проверка может проводиться двумя способами: – сравниваются между собой средние арифметические значения в каждой серии; – сравниваются оценки дисперсий в каждой серии. Проверка значимости различия средних арифметических. Осуществляется в следующей последовательности: 1. Находят средние арифметические результатов измерений двух серий (отдельно в первой серии и отдельно во второй):  ,  .2. Проверяют нормальность распределения результатов наблюдений в первой серии и во второй. 3. Находят дисперсии  результатов первой серии и второй  и  соответственно по формулам и  . (24)4. Находят среднее квадратическое отклонение результатов двух серий 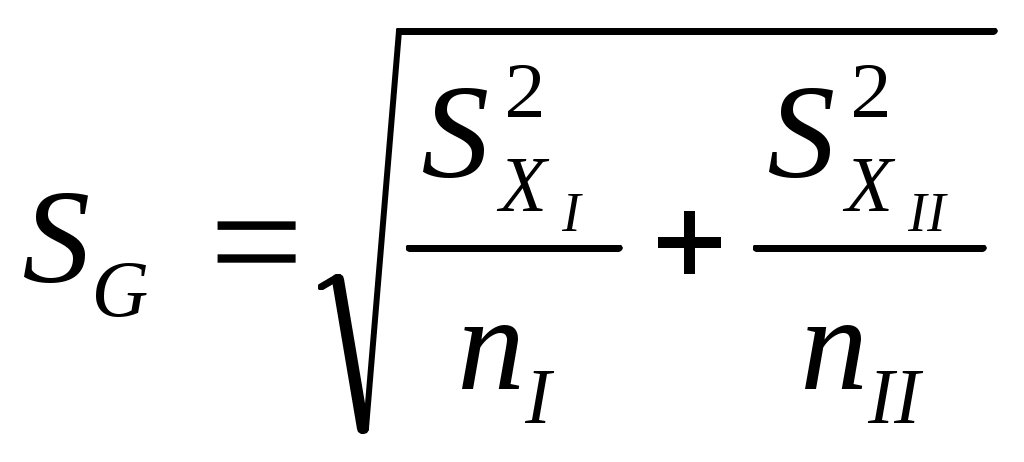  . (25)5. Находят разность средних арифметических  двух серий . (26)6. Выбирают доверительную вероятность Р икоэффициент Стьюдента  и определяют доверительный интервал для разности средних арифметических  .7. Если  , то различия между средними арифметическими незначительные. В противном случае – различия значимые.Сравнение оценок дисперсий двух серий. Серии с незначительными различиями дисперсий называются равнорассеянными, с существенными различиями – неравнорассеянными. Порядок сравнения оценок дисперсий двух серий по критерию Фишера следующий: 1. Из экспериментальных результатов измерений первой и второй серии находят средние арифметические: , .2. Проверяют нормальность распределения результатов наблюдений в первой серии и во второй. 3. Находят дисперсии результатов первой серии и второй и по формулам и  . (27)4. Определяют соотношение Fдвух дисперсий 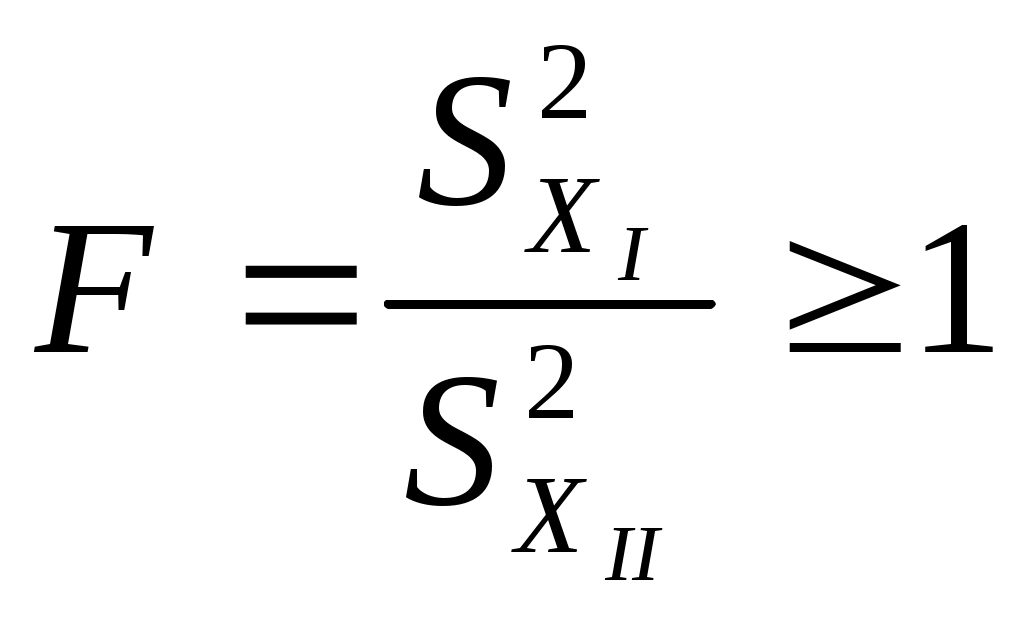 . (28)5. По уровню значимости  и степеням свободы результатов первой и второй серий  определяют критерий Фишера  по таблице распределения Фишера.6. Серии считаются равнорассеянными, если  , в противном случае серии являются неравнорассеянными.Экспериментальные данные, входящие в однородные серии можно рассматривать как единый массив и проводить обработку аналогично обработке результатов прямых многократных измерений. При обработке результатов неравнорассеянных серий с незначительно различающимися средними арифметическими учитывается ценность измерений, выполненных с большей точностью через коэффициенты весомости  , которые обратно пропорциональны дисперсии   . (29)Тогда средневзвешенное арифметическое 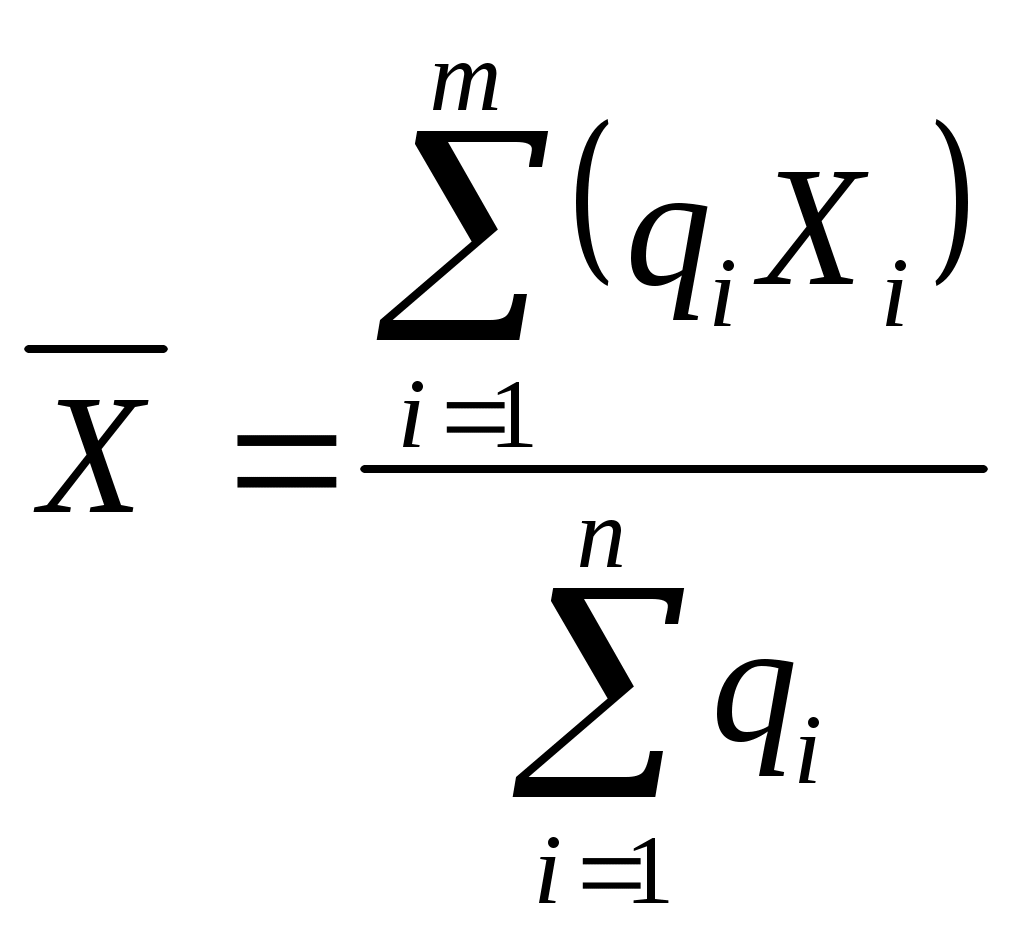 будет определяться следующим образом: . (30)Вопрос 4. Оценка неопределенности измерений Процесс оценивания неопределенности может быть представлен в виде следующих этапов. 1. Описание измерения, составление его модели и выявление источников неопределенности. Любой процесс измерения можно представить в виде последовательности выполняемых операций. Поэтому для описания измеряемой величины и выявления источников неопределенности целесообразно представить цепь преобразования измеряемой величины в виде схемы, отображающей последовательность процесса измерений. В большинстве случаев измеряемая величина Y не является прямо измеряемой, а зависит от N других измеряемых величин Х1, Х2 … ХN и выражается через функциональную зависимость  , (31)где –  – входные величины;  – выходная величина.Входные величины  , от которых зависит выходная величина , являются непосредственно измеряемыми величинами и сами могут зависеть от других величин, включая поправки и поправочные коэффициенты на систематические эффекты ,  и т. д.Описание измеряемой величины в виде функциональной зависимости (математической модели), связывающей измеряемую величину с параметрами, от которых она зависит, называется моделированием. Стадия моделирования является чрезвычайно важной, так как от правильности и тщательности составления модели измерения, которая определяется необходимой точностью, зависит количество источников неопределенности. С 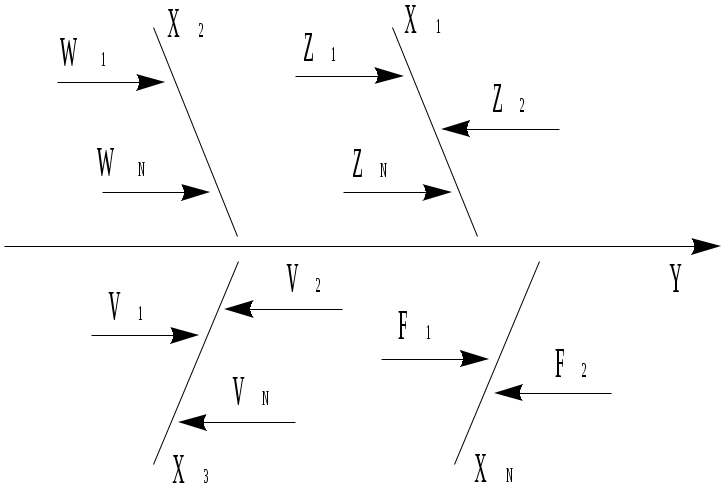 целью обобщения источников неопределенности измеряемую (выходную) величину и выявленные источники неопределенности: входные величины и величины, на них влияющие целесообразно представить на диаграмме «причина – следствие» (рис. 1): Рис. 1. Диаграмма «причина-следствие» Источниками неопределенности могут быть пробоотбор, условия хранения, аппаратурные эффекты, чистота реактивов, условия измерений, влияние пробы, вычислительные и случайные эффекты, влияние оператора. 2.Оценивание значений и стандартных неопределенностей входных величин. Следующим этапом после выявления источников неопределенности является количественное описание неопределенностей, возникающих от этих источников. Это может быть сделано двумя путями: – оцениванием неопределенности, возникающей от каждого отдельного источника с последующим суммированием составляющих; – непосредственным определением суммарного вклада в неопределенность от некоторых или всех источников с использованием данных об эффективности метода в целом. Показатели эффективности метода устанавливают в процессе его разработки и межлабораторных или внутрилабораторных исследований. К показателям эффективности относятся правильность, характеризуемая смещением, и прецизионность, характеризуемая повторяемостью, воспроизводимостью и промежуточной прецизионностью. Оценки эффективности могут включать не все факторы, поэтому влияние любых оставшихся следует оценить отдельно и затем просуммировать. Для каждой входной величины необходимо определить оценку и стандартную неопределенность. При этом все входные величины вследствие того, что их значения не могут быть точно известны, являются случайными непрерывными. Тогда оценками входных величин (  ), обозначаемыми малыми буквами, являются их математические ожидания, а стандартными неопределенностями  входных величин – стандартные отклонения. Оценку входных величин  и связанную с ней стандартную неопределенность получают из закона распределения вероятностей входной величины.Оценивание неопределенности от каждого источника возможно двумя способами: по типу А (путем статистического анализа ряда наблюдений) и по типу В (иным способом, чем статистический анализ ряда наблюдений). Исходными данными для оценивания стандартной неопределенности по типу А являются результаты многократных измерений  ;  На основании полученных результатов рассчитывается среднее арифметическое  по формуле (32), которое является оценкой входной величины , . (32) Стандартная неопределенность, связанная с оценкой  является экспериментальным стандартным отклонением среднего значения и равна положительному квадратному корню из экспериментальной дисперсии среднего значения. Стандартная неопределенность вычисляется по формуле . (33)для результата измерения  , вычисленного как среднее арифметическое.Исходными данными для оценивания стандартной неопределенности по типу В является следующая априорная информация: – данные предшествовавших измерений величин, входящих в уравнение измерения; – сведения о виде распределения вероятностей; – данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих приборов и материалов; – неопределенности констант и справочных данных; – данные поверки, калибровки, сведения изготовителя о приборе и др. Если оценка 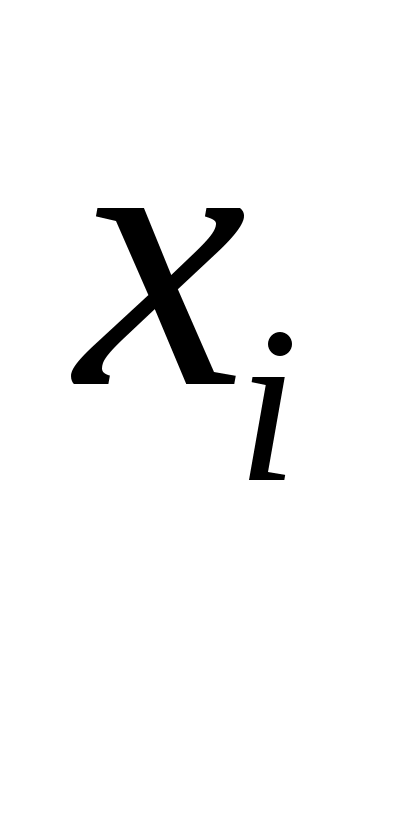 берется из спецификации изготовителя, свидетельства о поверке, справочника или другого источника, то неопределенность обычно дается как интервал  отклонения входной величины от ее оценки. Имеющуюся информацию о величинах  необходимо правильно описать с помощью функции распределения вероятностей. Для определения стандартной неопределенности входных величин необходимо воспользоваться законом распределения вероятностей . 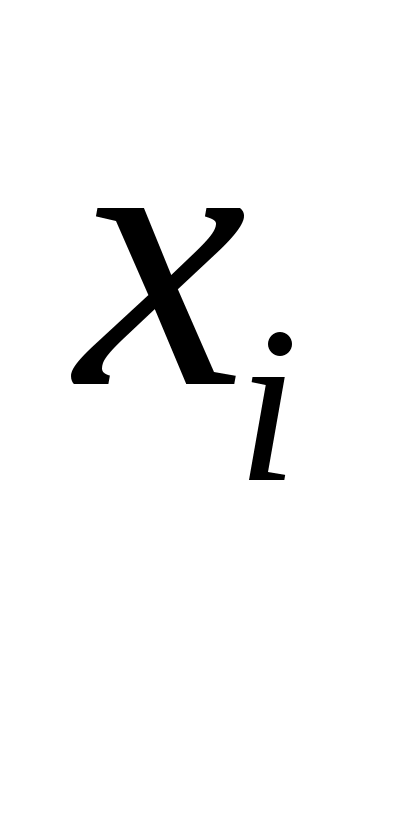При этом чаще всего используют следующие основные законы распределения:– прямоугольное (равномерное); – треугольное; – нормальное (Гаусса). Формулы и способы применения представлены в табл. 4. |
