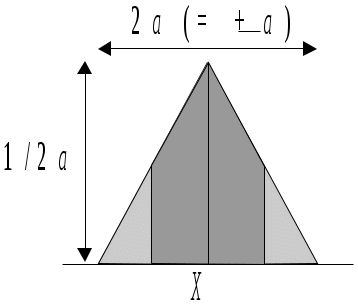Таблица 4
Вид функции
плотности
вероятности
|
Способ применения
|
Стандартная неопределенность
|
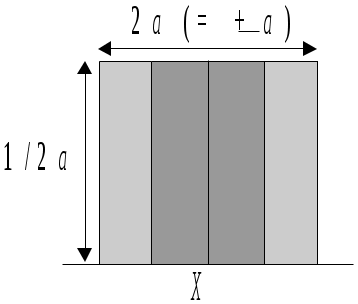
Прямоугольное распределение
|
|
– об измеряемой величине известно только, что ее значение наверняка лежит в определенной области и что каждое значение между границами этой области с одинаковой вероятностью может приниматься в расчет;
– сертификат или другой документ дает пределы без определения уровня доверия (например, 25мл 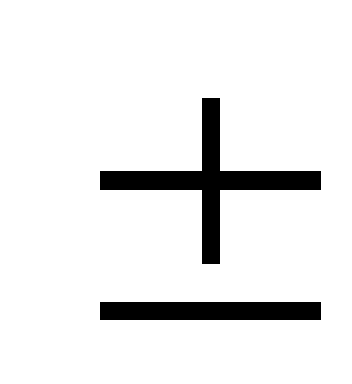 0,05 мл); 0,05 мл);
– оценка получена в форме максимальных значений (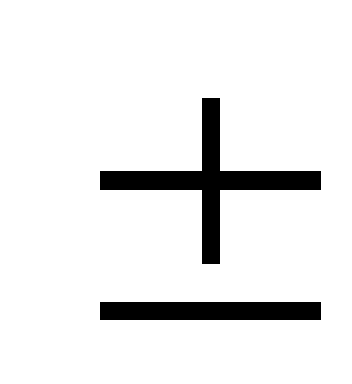 а) с неизвестной формой распределения. а) с неизвестной формой распределения.
|
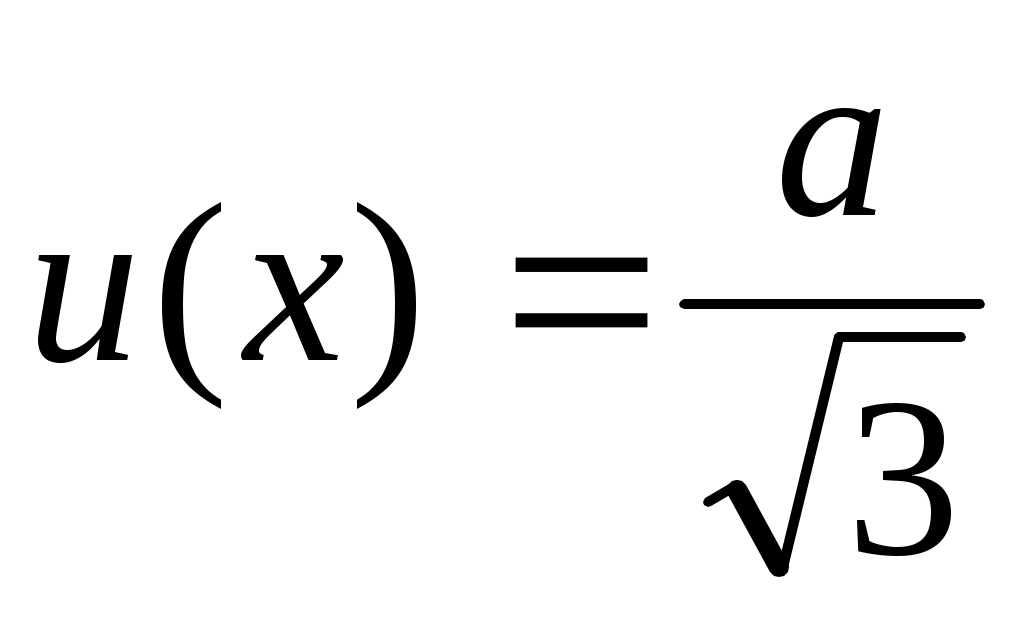
|
Треугольное распределение
|
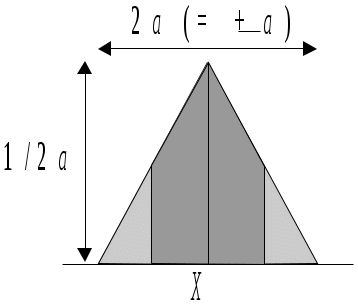
|
– доступная информация относительно значений величины менее ограничена, чем для прямоугольного распределения. Значения возле среднего значения более вероятны, чем у границ;
– оценка получена в форме максимальных значений диапазона ( а), описанного симметричным распределением вероятностей; а), описанного симметричным распределением вероятностей;
– когда величина является суммой или разностью двух величин, распределение вероятностей значений которых описывается прямоугольным законом с одинаковыми диапазонами.
|
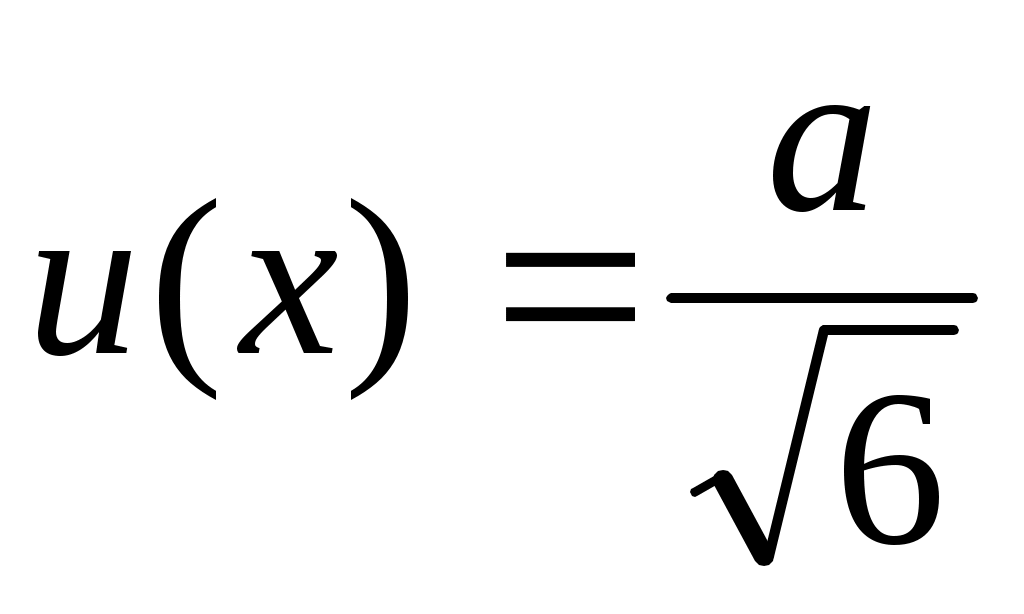
|
Нормальное распределение
|
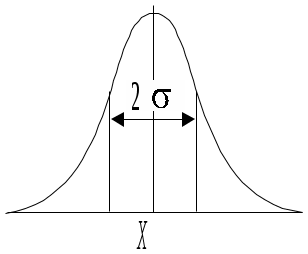
|
Оценка получена из повторных наблюдений случайно изменяющегося процесса.
Неопределенность дана в форме:
– стандартного отклонения наблюдений;
– относительного стандартного отклонения 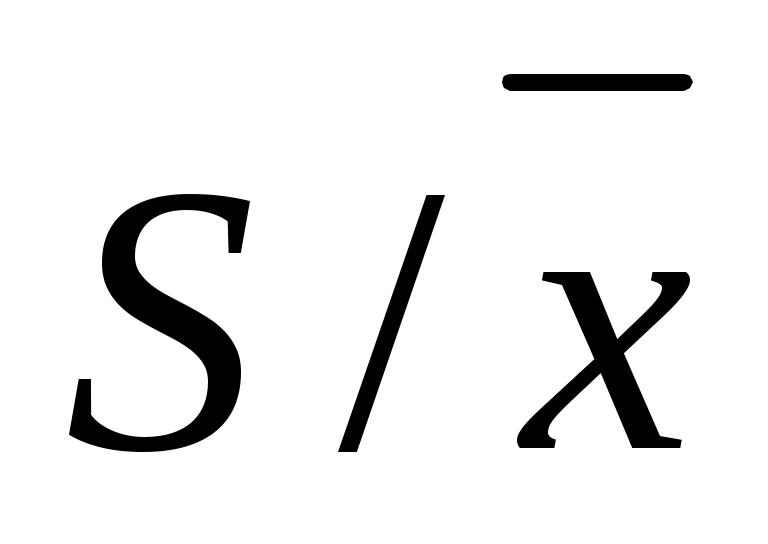 ; ;
– коэффициента дисперсии СV% без установления вида распределения.
Неопределенность дается в форме 95%-го или другого интервала доверия  без указания вида распределения. без указания вида распределения.
|
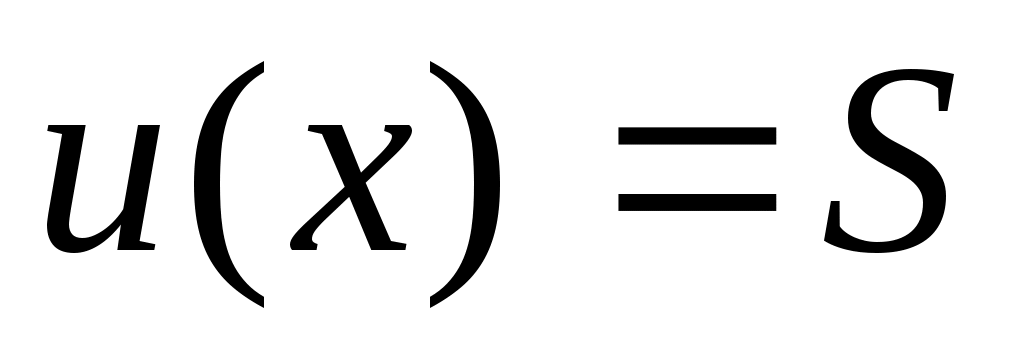
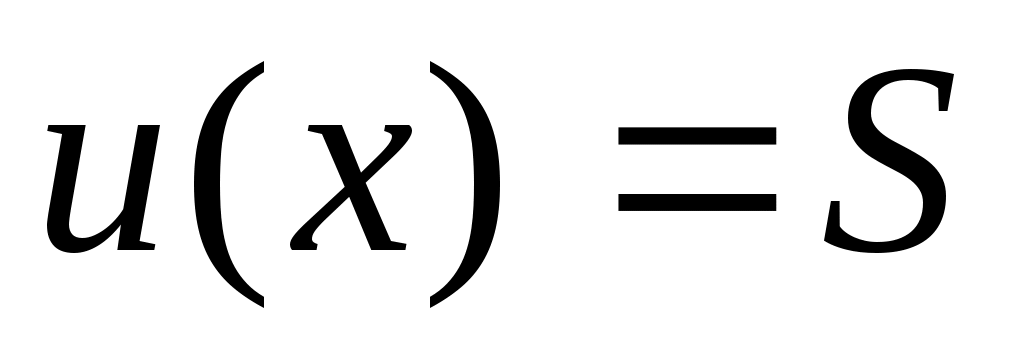
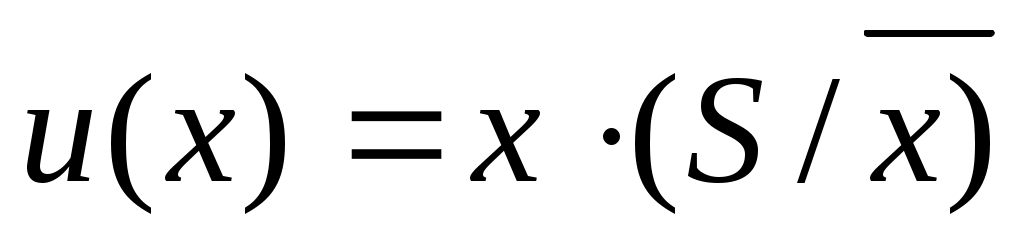
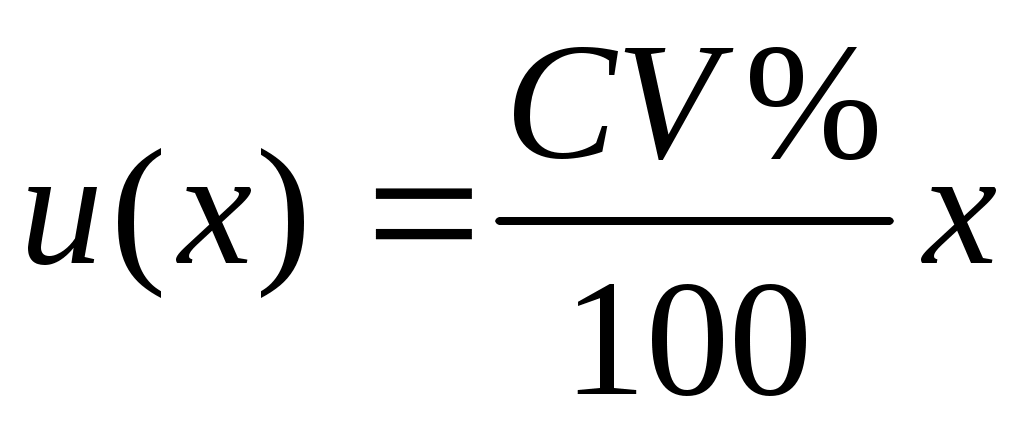
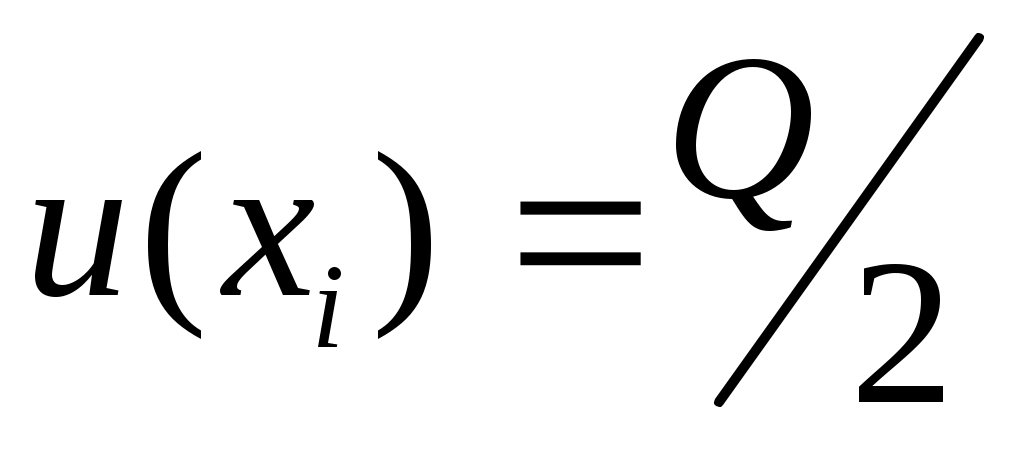 (при Р = 0,95). (при Р = 0,95).
|
3. Анализ корреляций. Две входные величины могут быть независимы или связаны между собой (коррелированны). В концепции неопределенности имеется в виду корреляция «логическая», а не математическая. Например, может существовать значительная корреляция между двумя входными величинами, если при их определении используют один и тот же измерительный прибор, физический эталон или справочные данные, имеющие значительную стандартную неопределенность.
Мерой взаимной корреляции двух случайных величин является ковариация. Если две входные величины 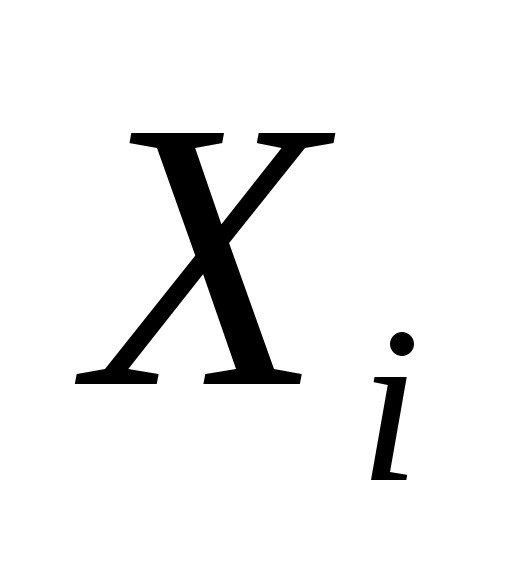 и и 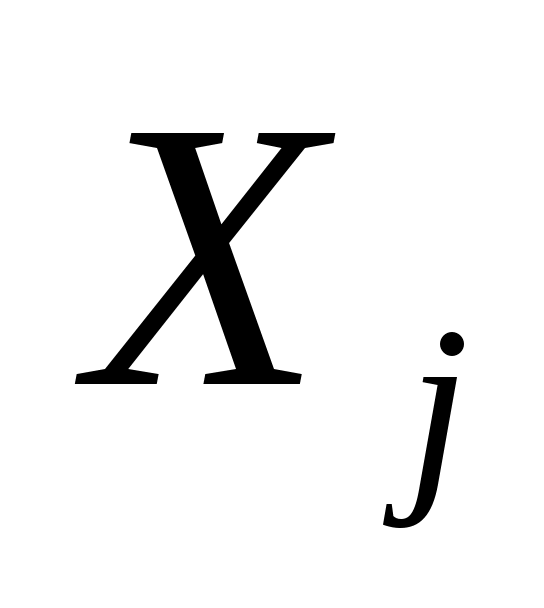 являются коррелированными, т. е. зависимыми друг от друга, то при оценивании суммарной стандартной неопределенности должна учитываться их ковариация являются коррелированными, т. е. зависимыми друг от друга, то при оценивании суммарной стандартной неопределенности должна учитываться их ковариация 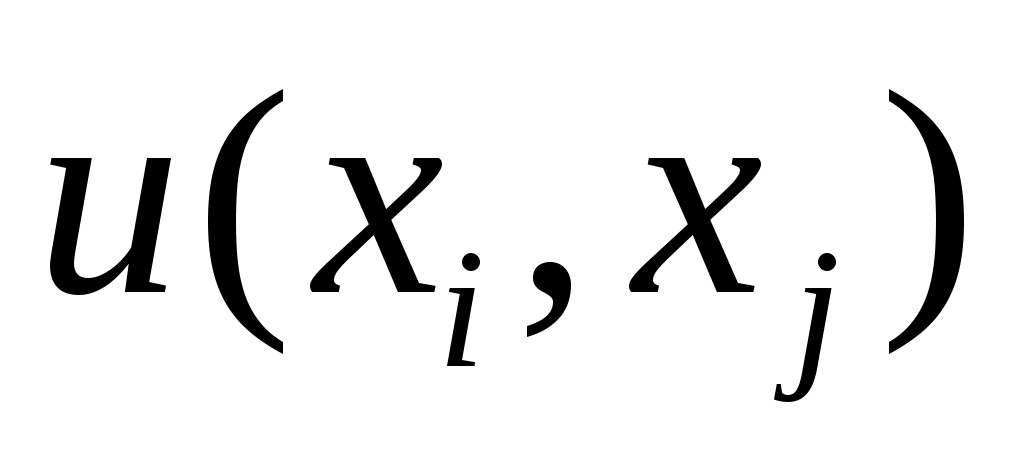 , которая оценивается по следующей формуле: , которая оценивается по следующей формуле:
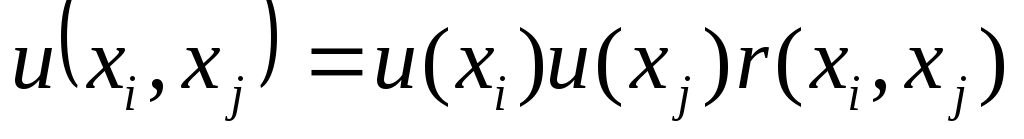 при при 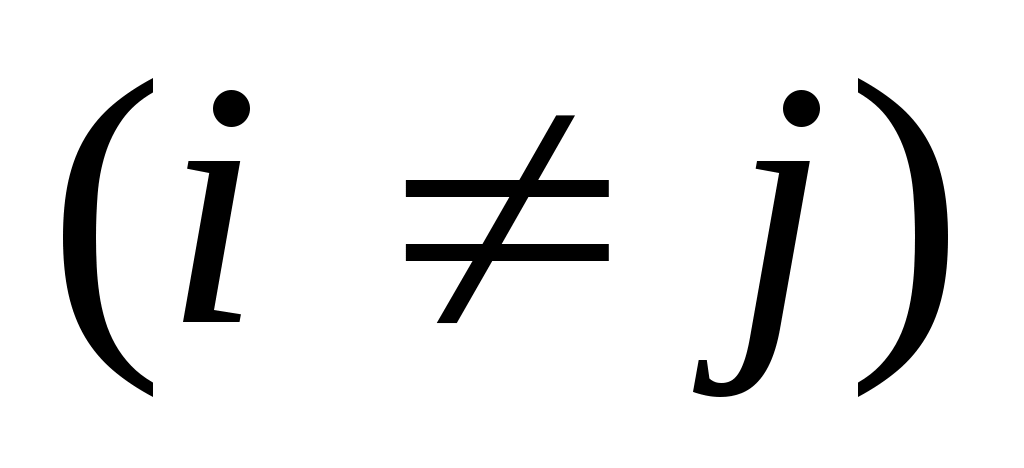 , (34) , (34)
где 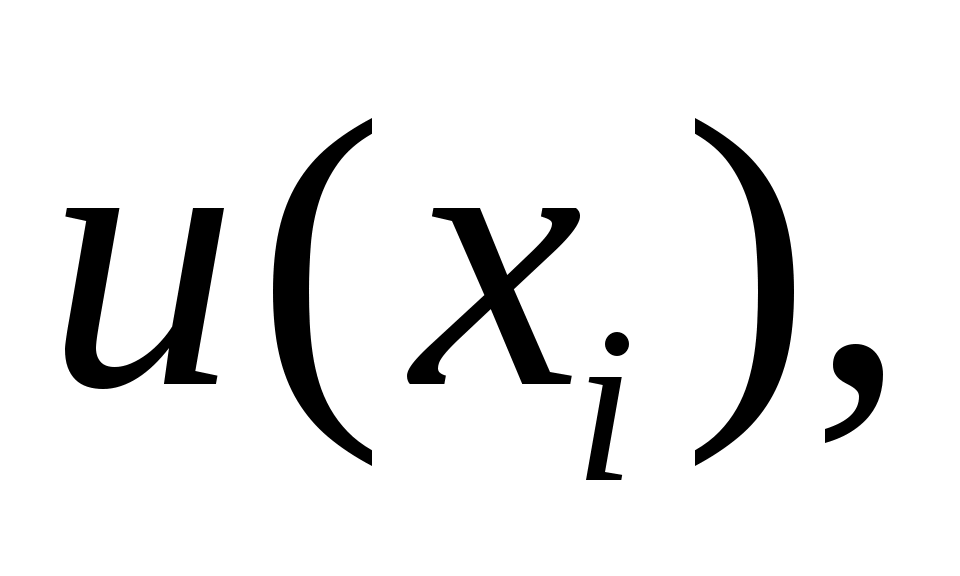 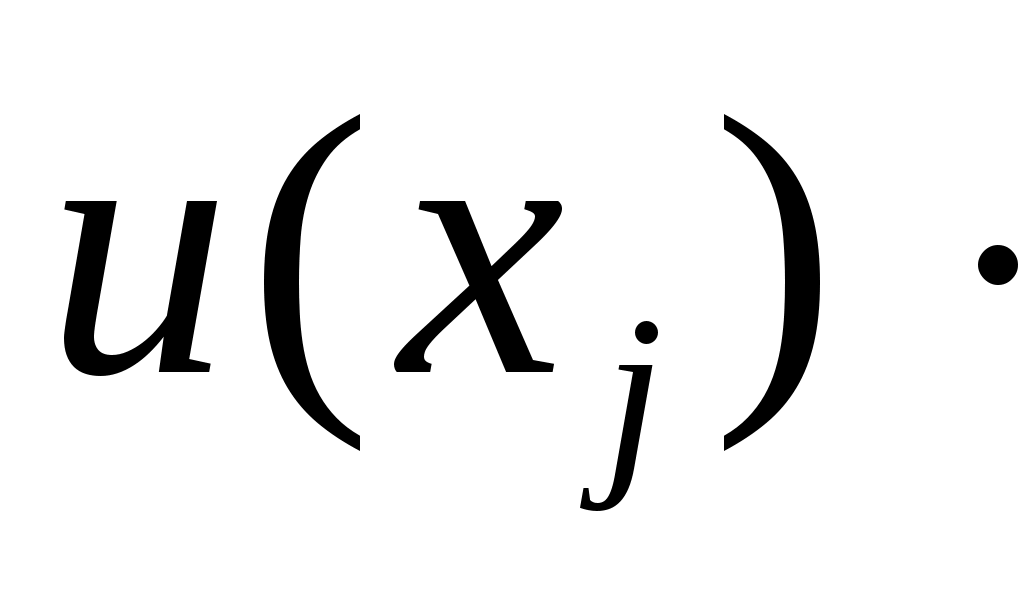 – стандартные неопределенности; – стандартные неопределенности; 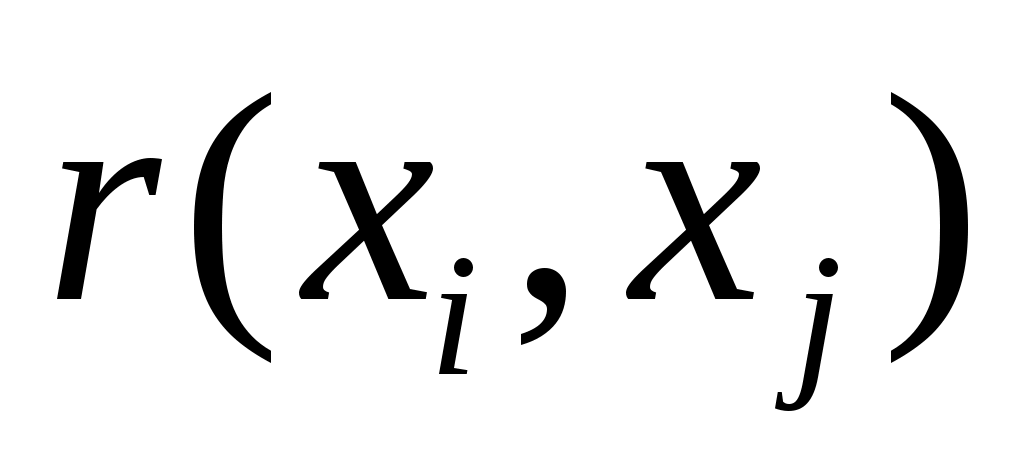 – коэффициент корреляции. – коэффициент корреляции.
Для расчета коэффициента корреляции используются согласованные пары измерений 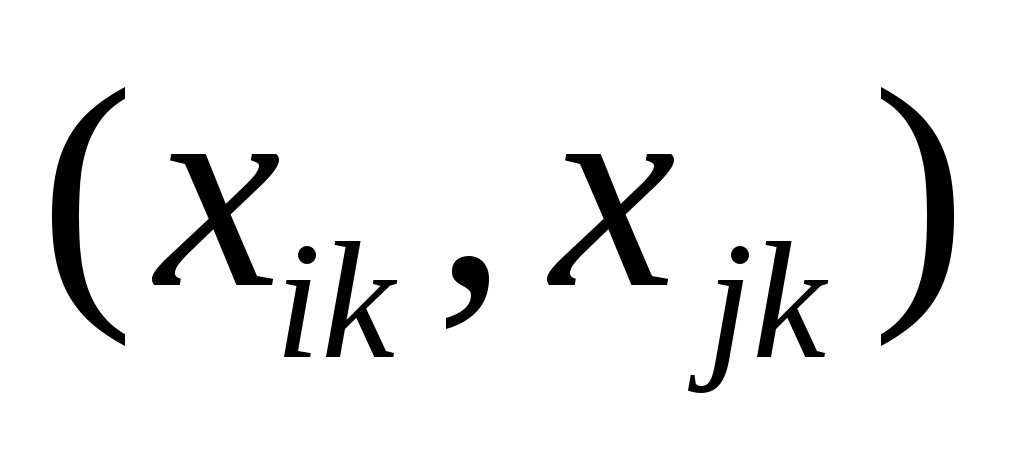 ; ; 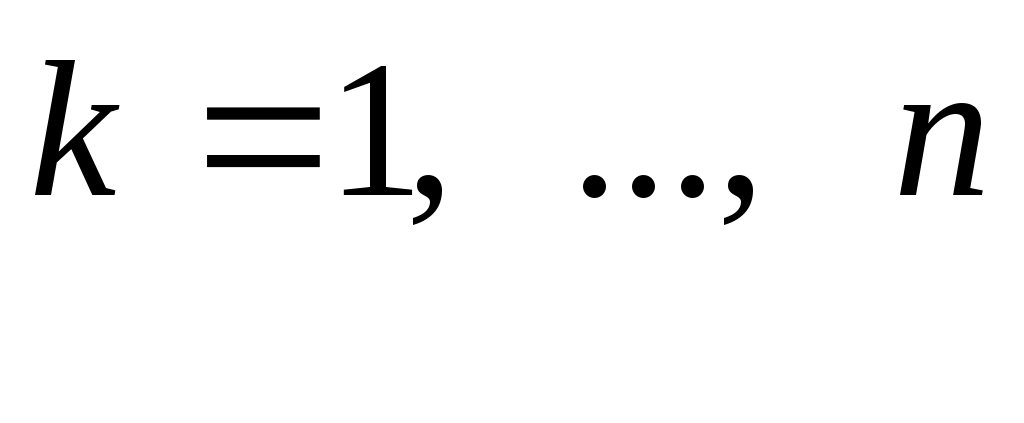
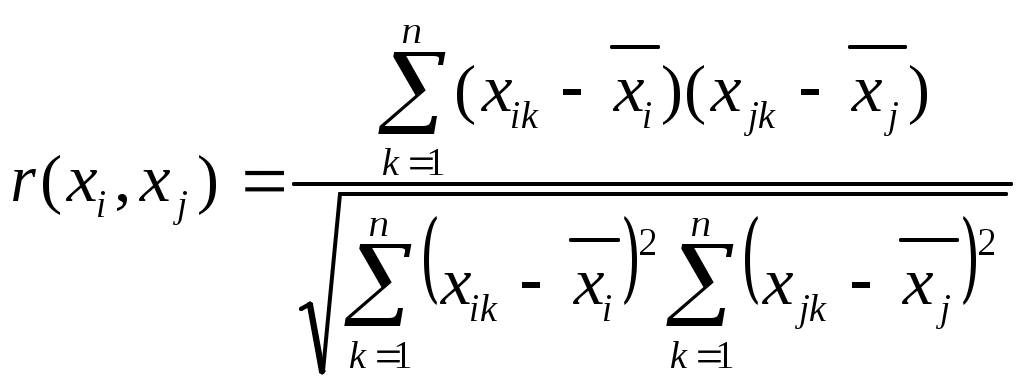 . (35) . (35)
4. Расчет оценки выходной величины. Оценка выходной величины 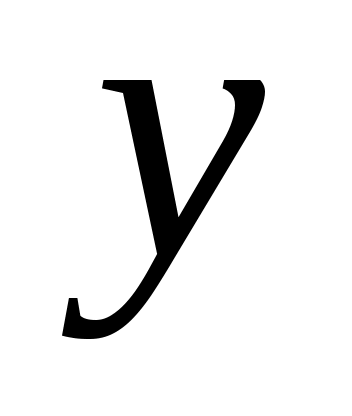 является результатом измерения. Эту оценку получают из уравнения связи, заменяя входные величины является результатом измерения. Эту оценку получают из уравнения связи, заменяя входные величины 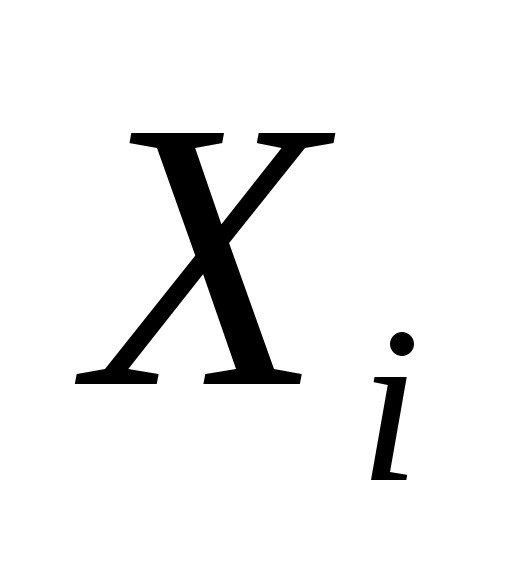 их оценками их оценками 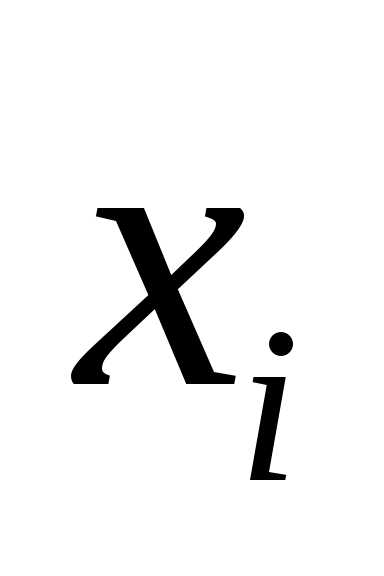
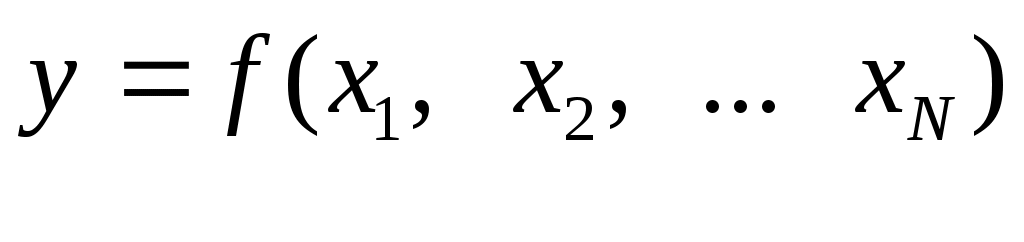 . (36) . (36)
5. Расчет стандартной неопределенности выходной величины. Стандартная неопределенность выходной величины 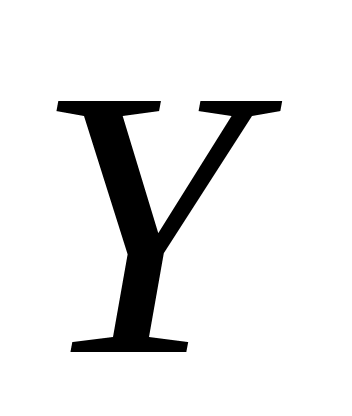 представляет собой стандартное отклонение оценки выходной величины или результата измерения и характеризует разброс значений, которые могут быть с достаточным основанием приписаны измеряемой величине. Определяется суммированием стандартной неопределенности входных величин представляет собой стандартное отклонение оценки выходной величины или результата измерения и характеризует разброс значений, которые могут быть с достаточным основанием приписаны измеряемой величине. Определяется суммированием стандартной неопределенности входных величин 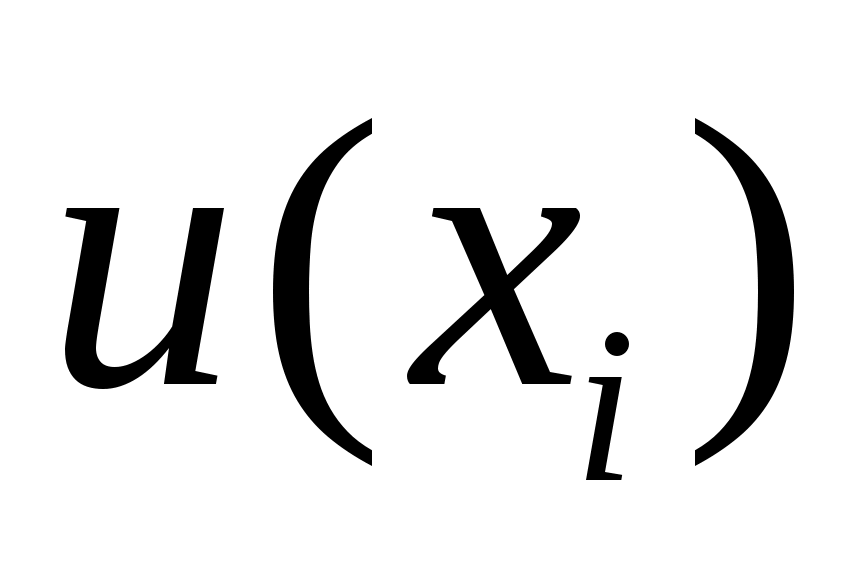 и является суммарной, или комбинированной стандартной неопределенностью, обозначаемой и является суммарной, или комбинированной стандартной неопределенностью, обозначаемой 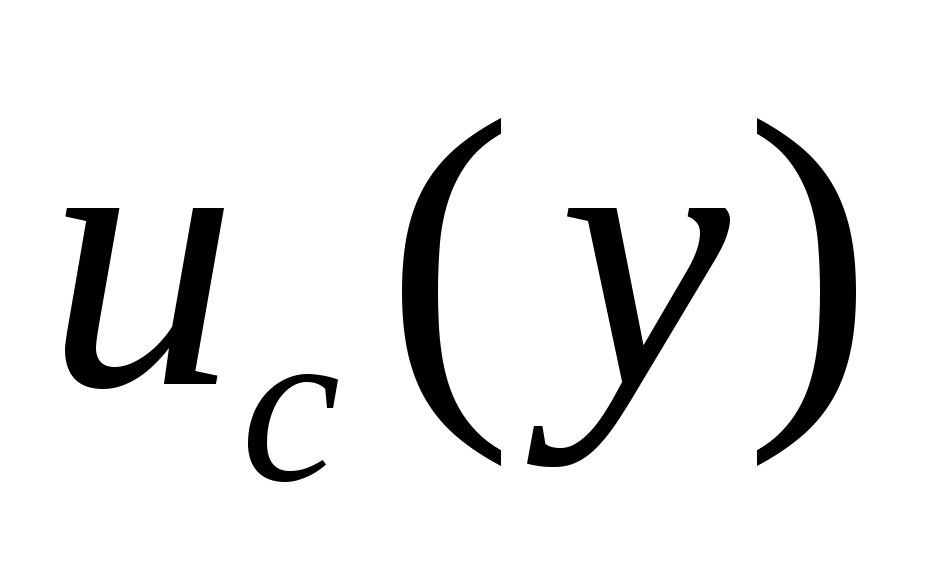 . .
Применяемый для суммирования метод в терминах концепции неопределенности называется законом распределения неопределенностей, или корнем из суммы квадратов.
В случае некоррелированных входных величин суммарная стандартная неопределенность рассчитывается по формуле
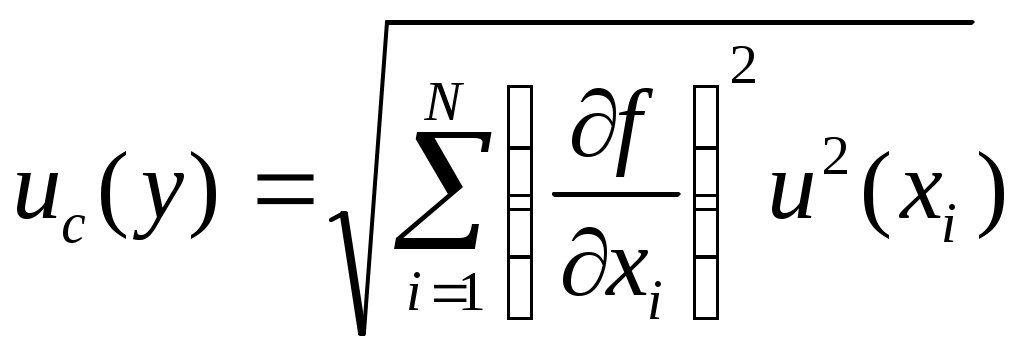 , (37) , (37)
где 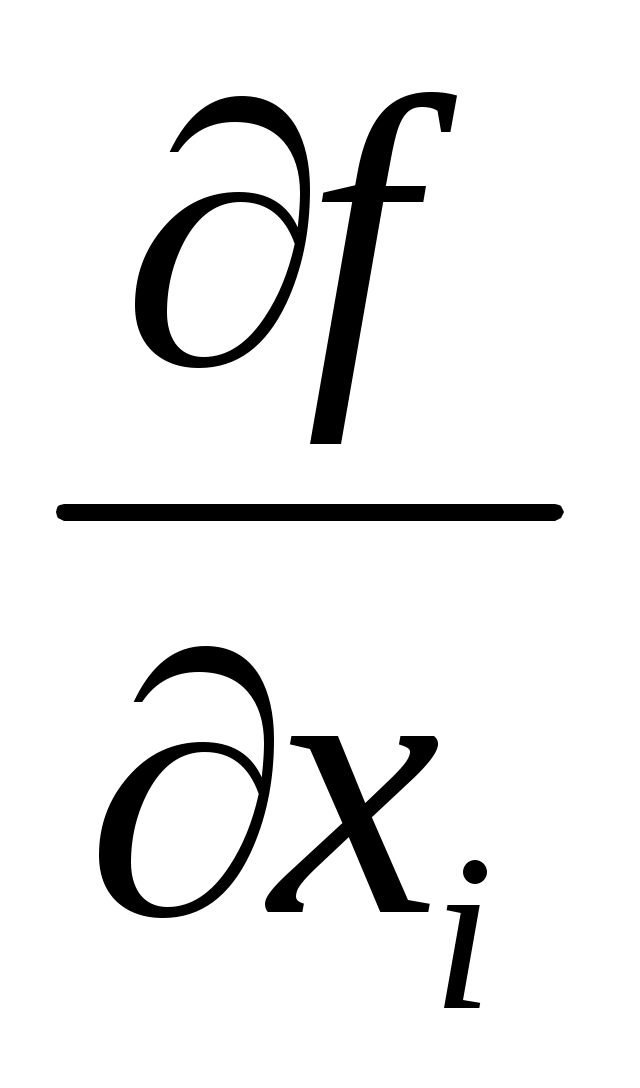 – частная производная функции – частная производная функции 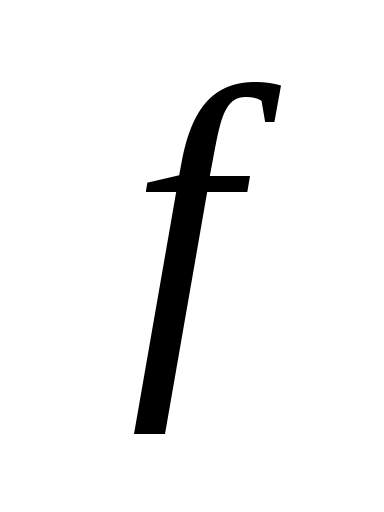 по аргументу по аргументу 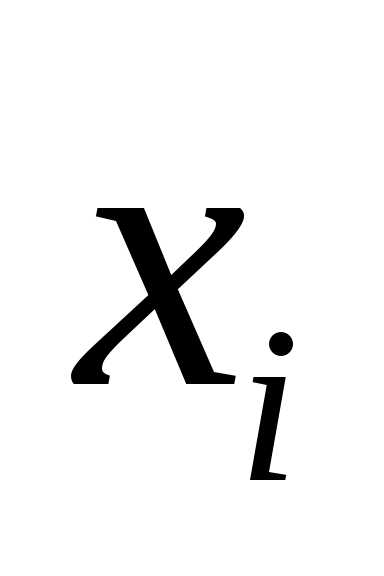 ; ; 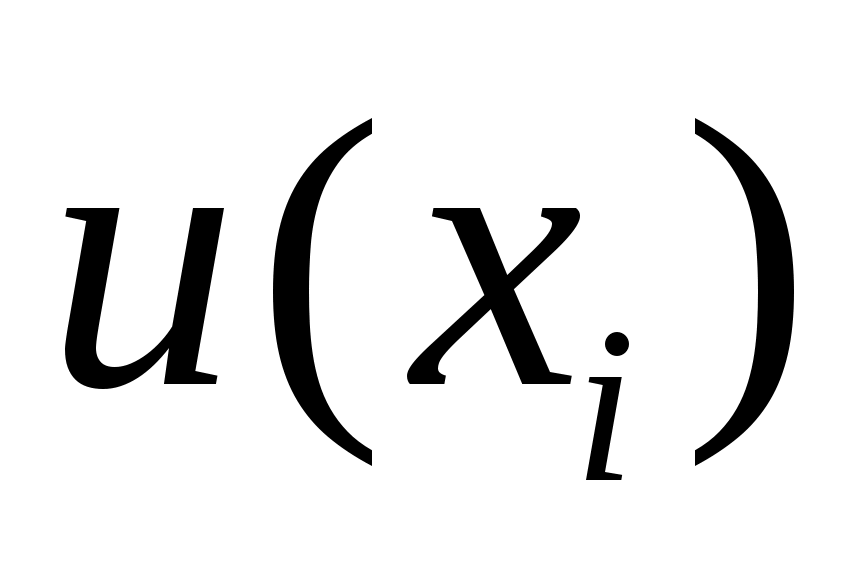 – стандартная неопределенность, оцененная по типу А или В. – стандартная неопределенность, оцененная по типу А или В.
В случае коррелированных входных величин
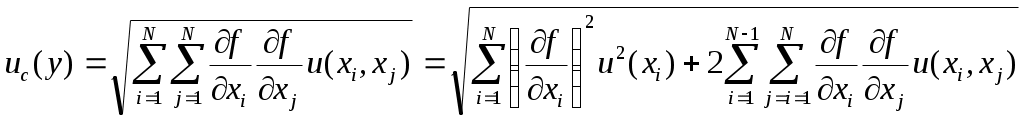 , (38) , (38)
где 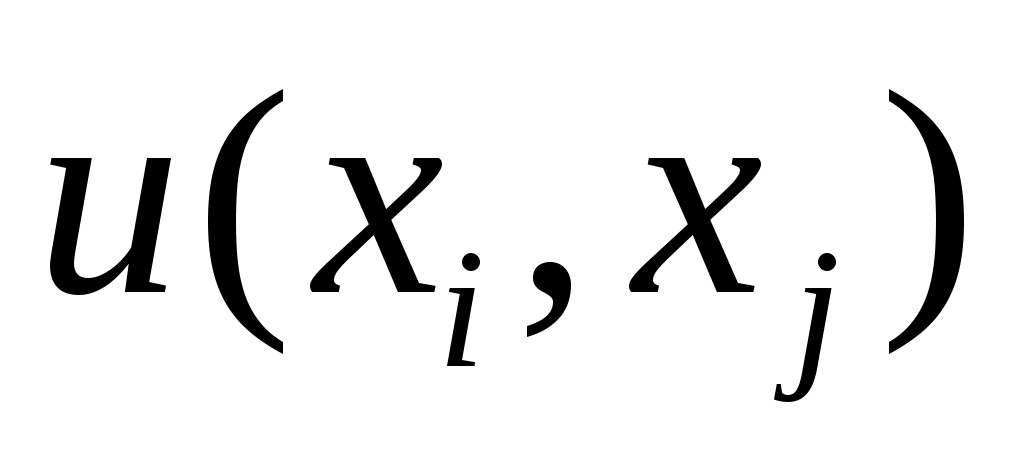 определяется по формуле (34). определяется по формуле (34).
Частные производные называются коэффициентом чувствительности 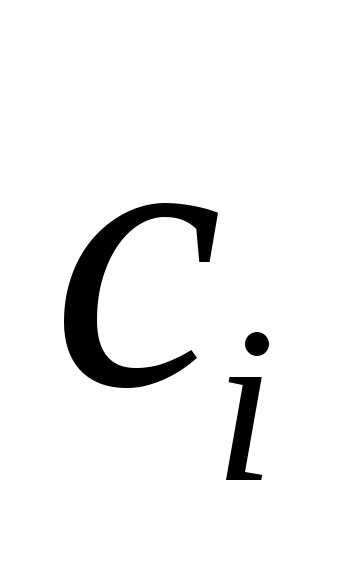 и показывают, как выходная величина и показывают, как выходная величина 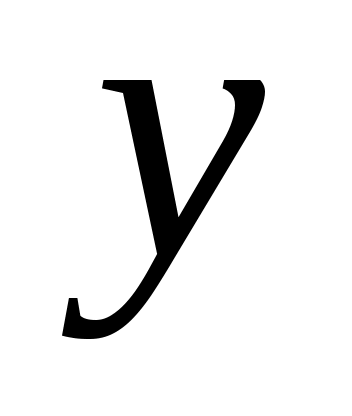 изменяется с изменением значения входных оценок изменяется с изменением значения входных оценок 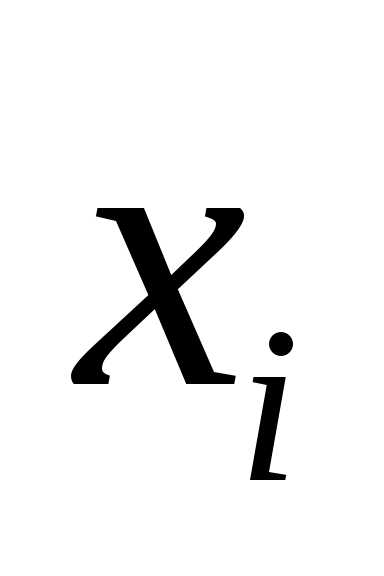 : : 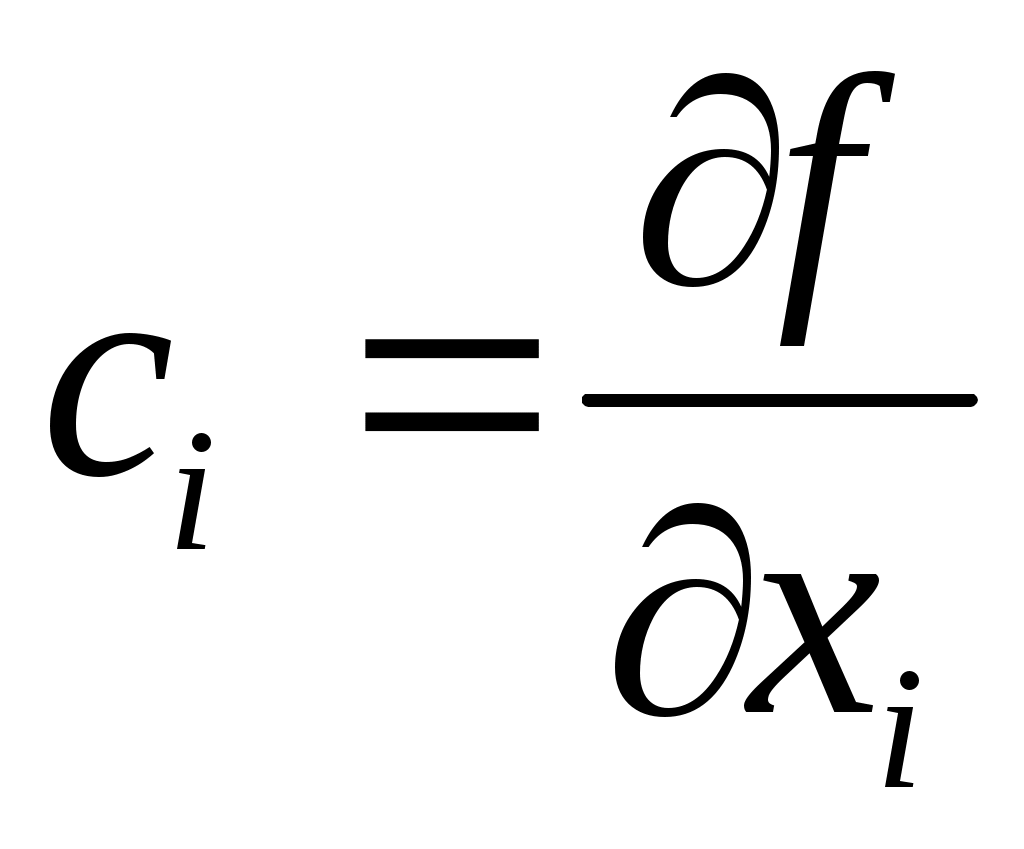 . .
С учетом 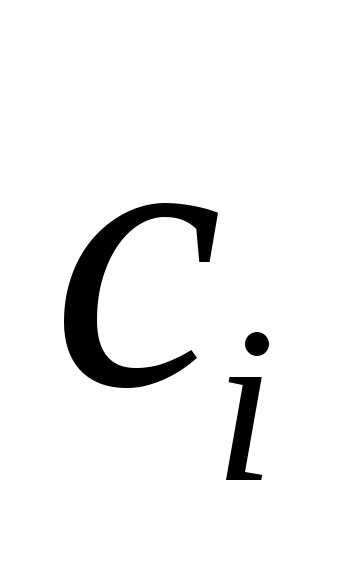 формулы преобразуются в следующие выражения: формулы преобразуются в следующие выражения:
– в случае некоррелированных входных величин
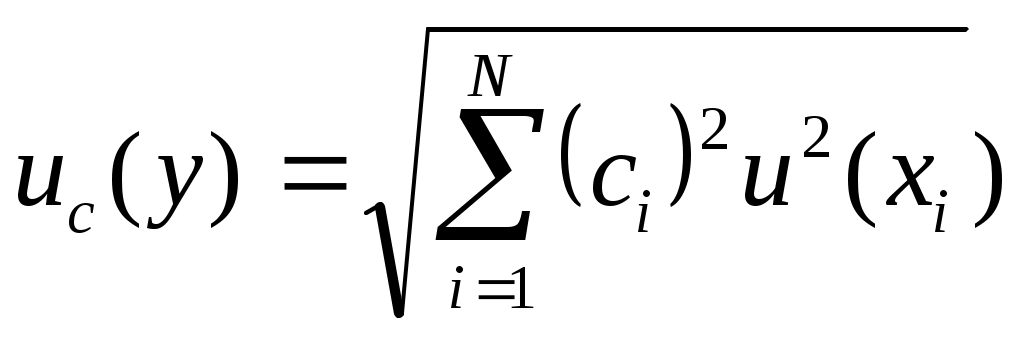 = =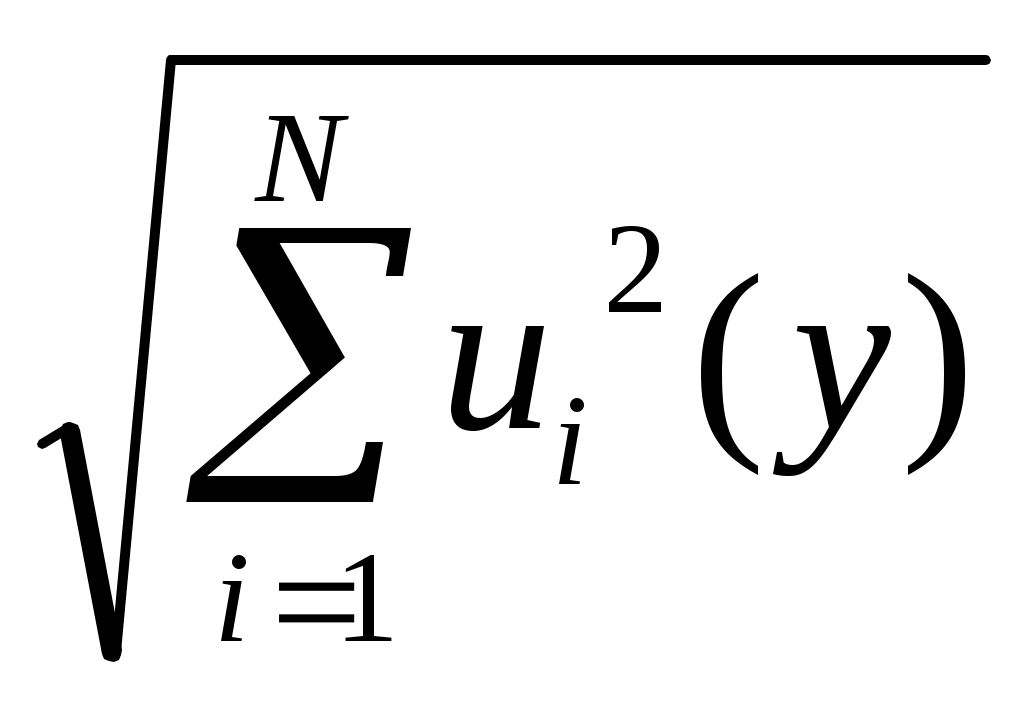 , (39) , (39)
– в случае коррелированных входных величин
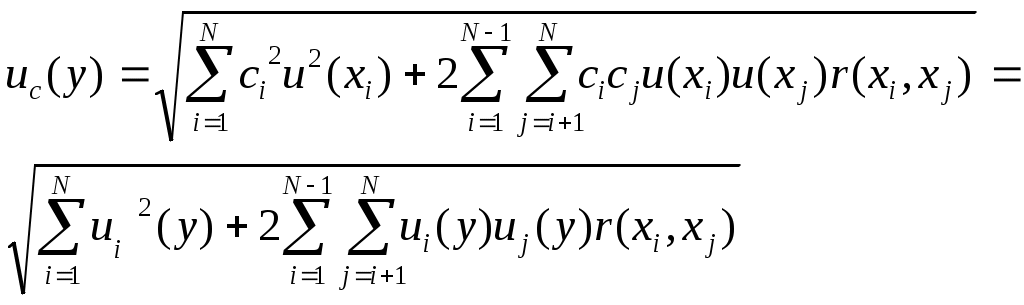 , (40) , (40)
где 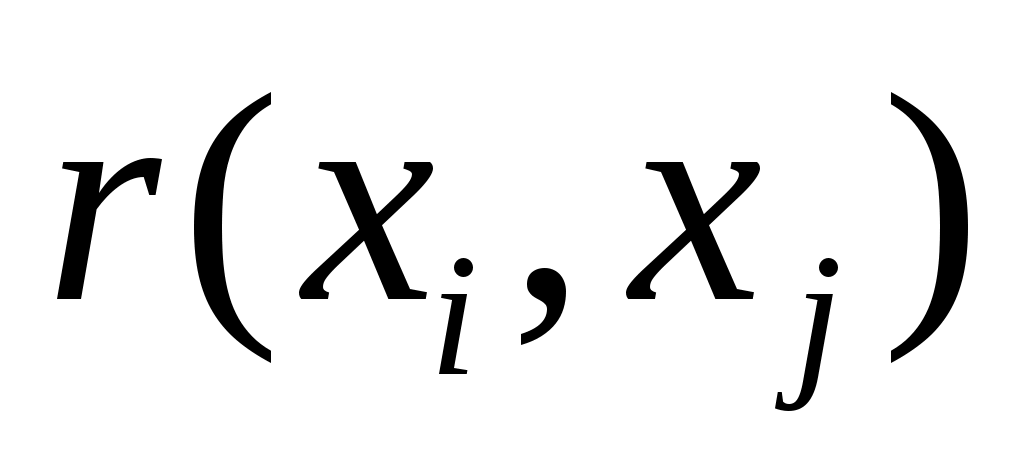 определяется по формуле (35). определяется по формуле (35).
Величина 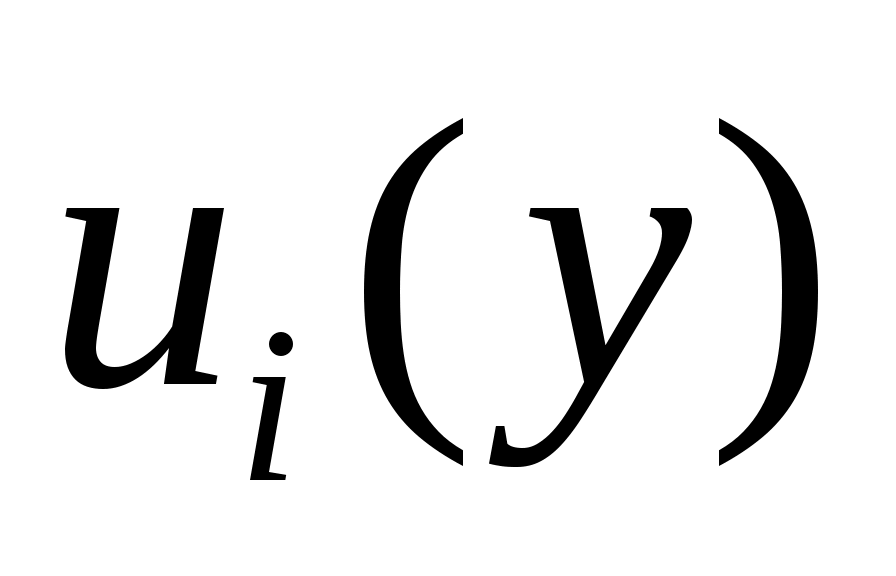  является вкладом в стандартную неопределенность, связанную с оценкой является вкладом в стандартную неопределенность, связанную с оценкой 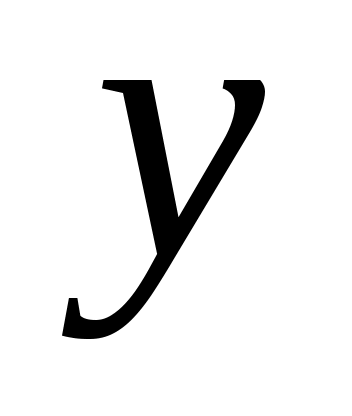 выходной величины, которая получается из стандартной неопределенности, связанной с оценкой входной величины выходной величины, которая получается из стандартной неопределенности, связанной с оценкой входной величины 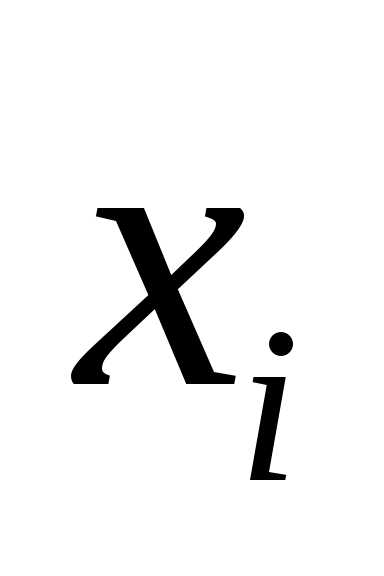 , по следующей формуле: , по следующей формуле:
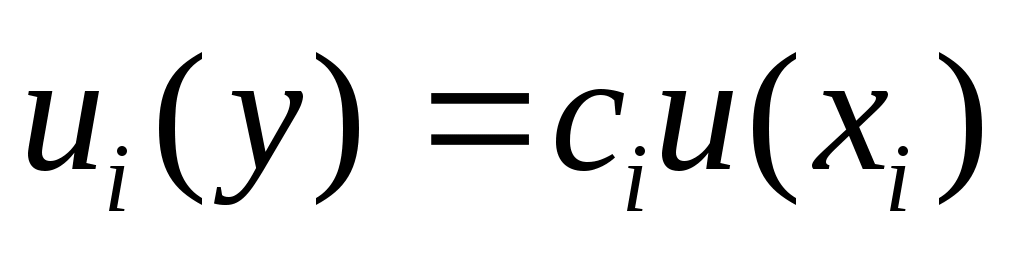 . (41) . (41)
Во многих случаях общие выражения для суммирования неопределенностей сокращаются до гораздо более простых формул.
Так, если функция модели 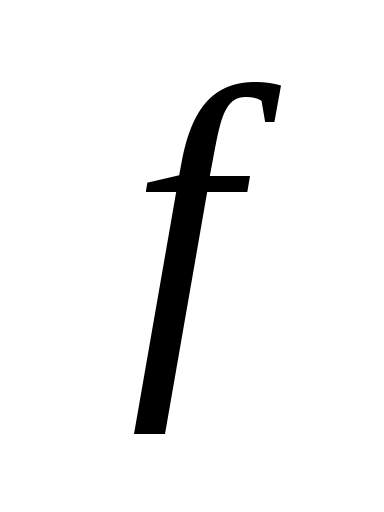 является суммой или разностью некоррелированных входных величин является суммой или разностью некоррелированных входных величин 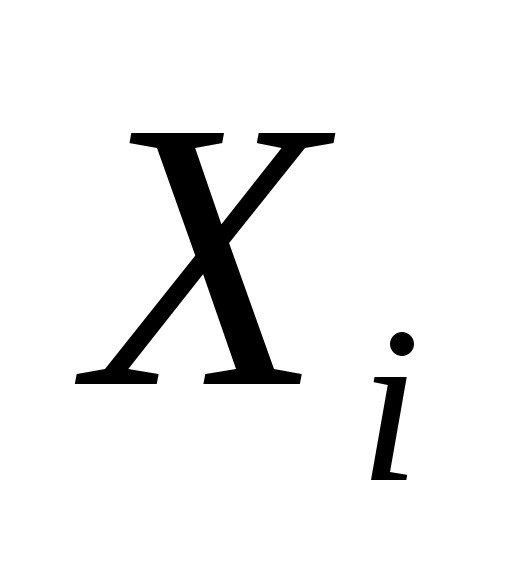 , например , например 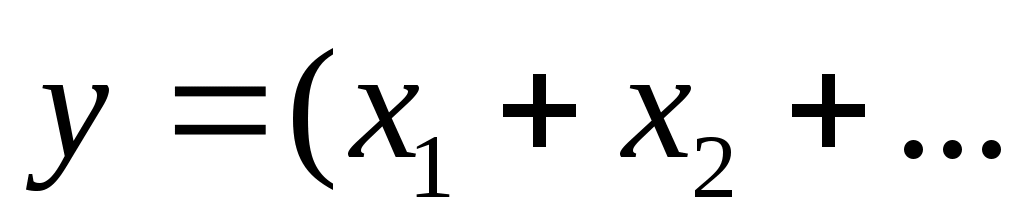 ) , то суммарная стандартная неопределенность ) , то суммарная стандартная неопределенность 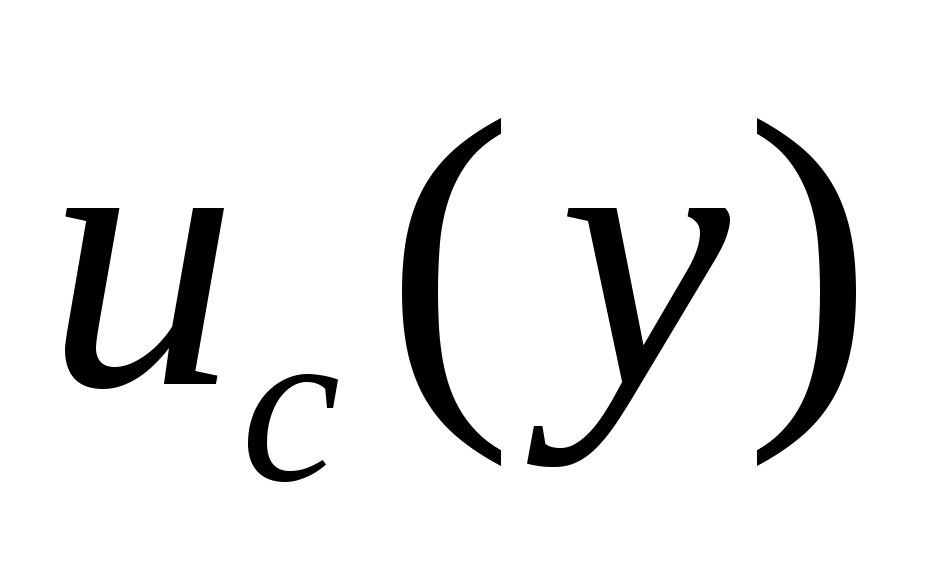 определяется выражением: определяется выражением:
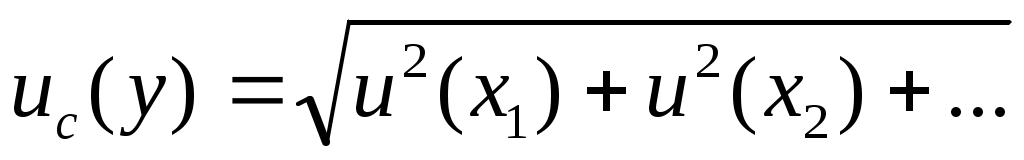 . (42) . (42)
Если функция модели 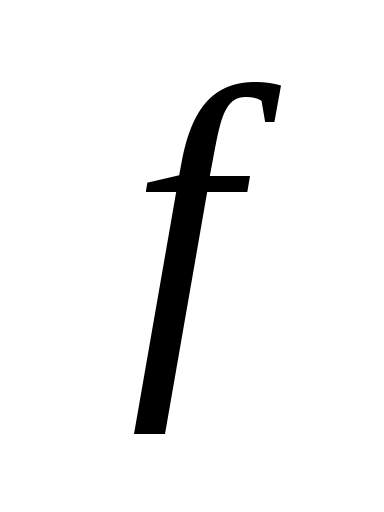 является произведением или отношением некоррелированных входных величин является произведением или отношением некоррелированных входных величин 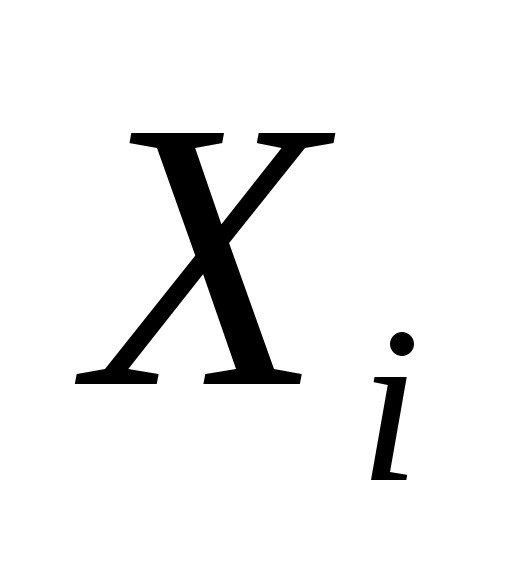 , то суммарная стандартная неопределенность , то суммарная стандартная неопределенность 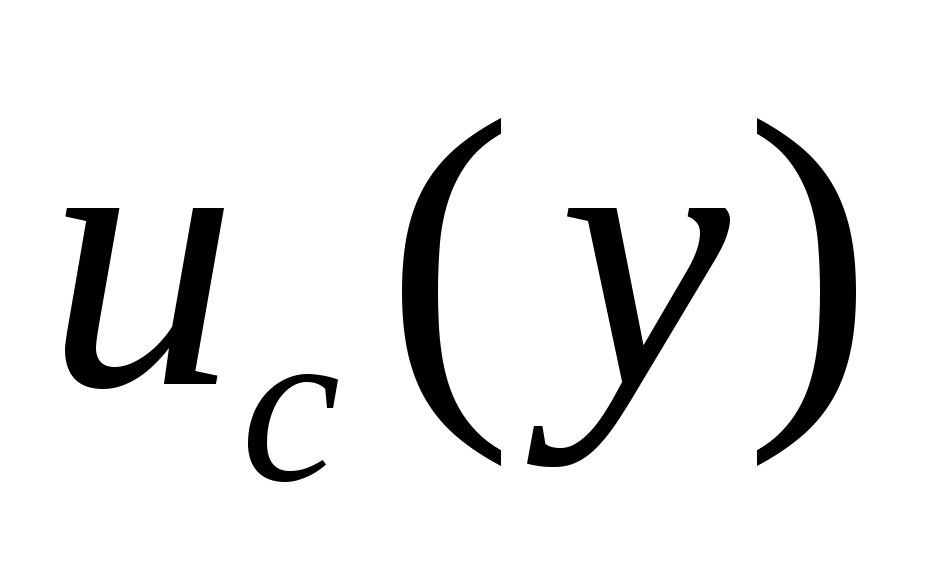 определяется выражением: определяется выражением:
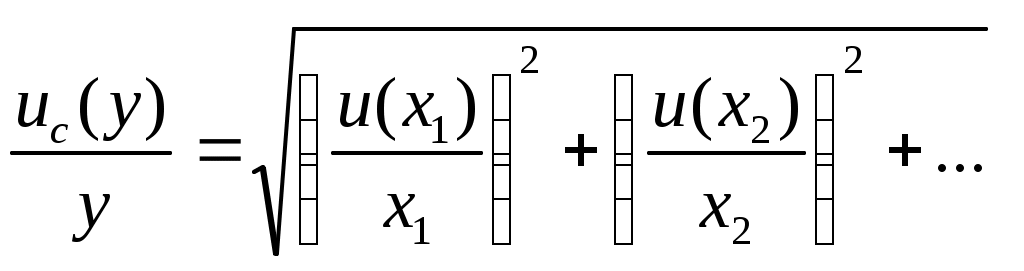 . (43) . (43)
где 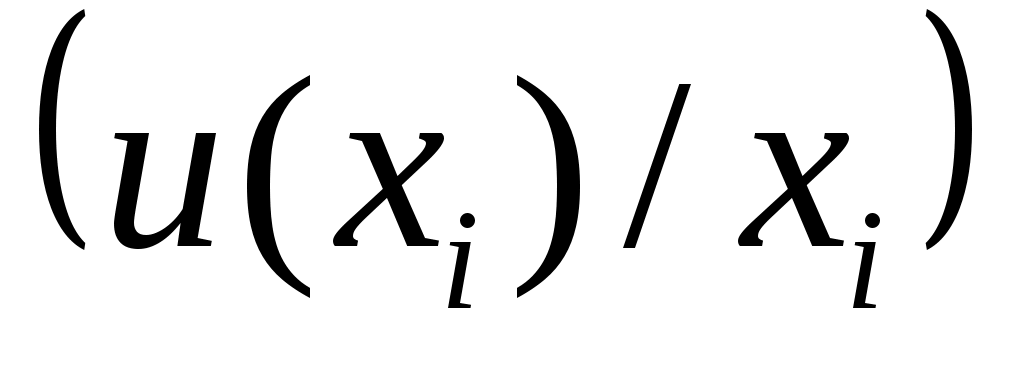 – неопределенности параметров, выраженные в виде относительных стандартных отклонений. – неопределенности параметров, выраженные в виде относительных стандартных отклонений.
6.Расчет расширенной неопределенности. Расширенная неопределенность 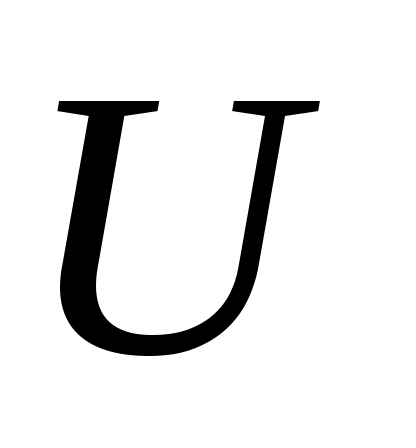 получают путем умножения стандартной неопределенности выходной величины получают путем умножения стандартной неопределенности выходной величины 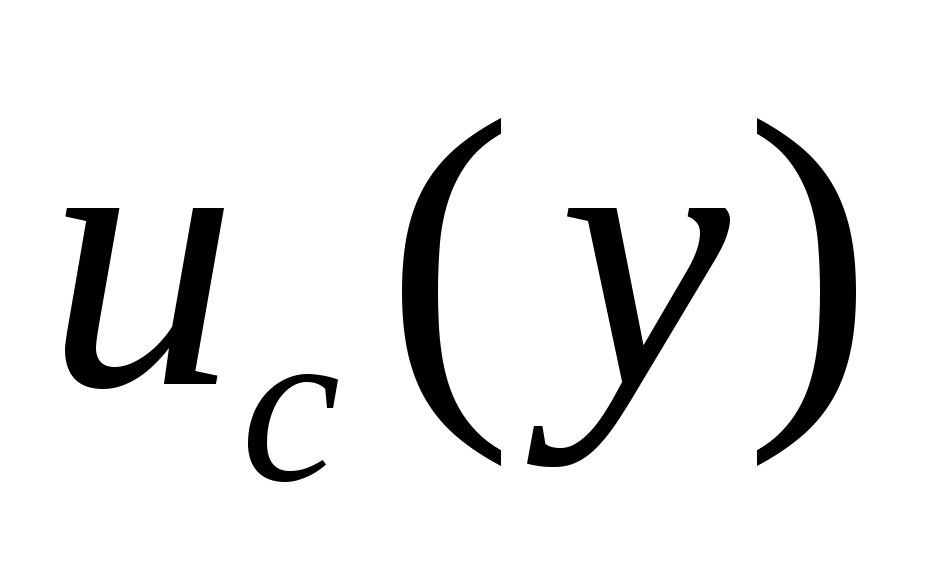 на коэффициент охвата на коэффициент охвата 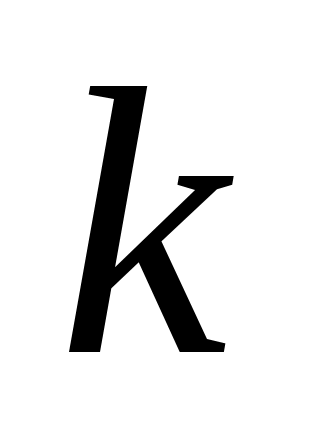 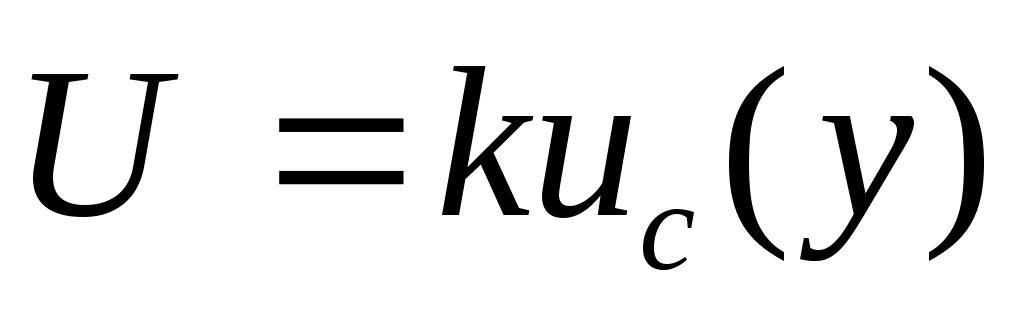 . При выборе значения коэффициента охвата следует учитывать: . При выборе значения коэффициента охвата следует учитывать:
– требуемый уровень достоверности;
– какую-либо информацию о предполагаемом распределении;
– информацию о количестве наблюдений, использованных для оценки случайных эффектов.
Коэффициент охвата 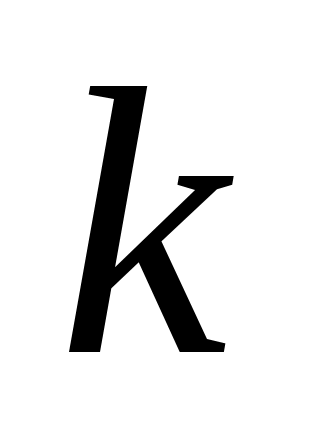 при оценивании расширенной неопределенности выбирают в соответствии со следующими рекомендациями. при оценивании расширенной неопределенности выбирают в соответствии со следующими рекомендациями.
В случаях, когда измеряемой величине может приписываться нормальное распределение вероятностей, коэффициент охвата 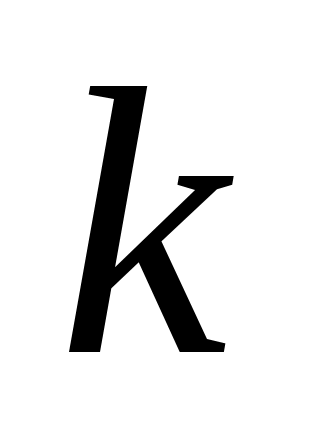 определяется как квантиль нормированного нормального распределения при уровне доверия определяется как квантиль нормированного нормального распределения при уровне доверия 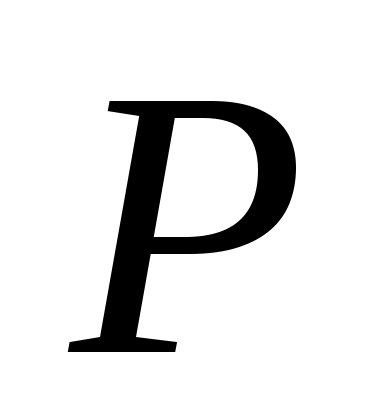 (табл. 5). (табл. 5).
|
 Скачать 0.71 Mb.
Скачать 0.71 Mb.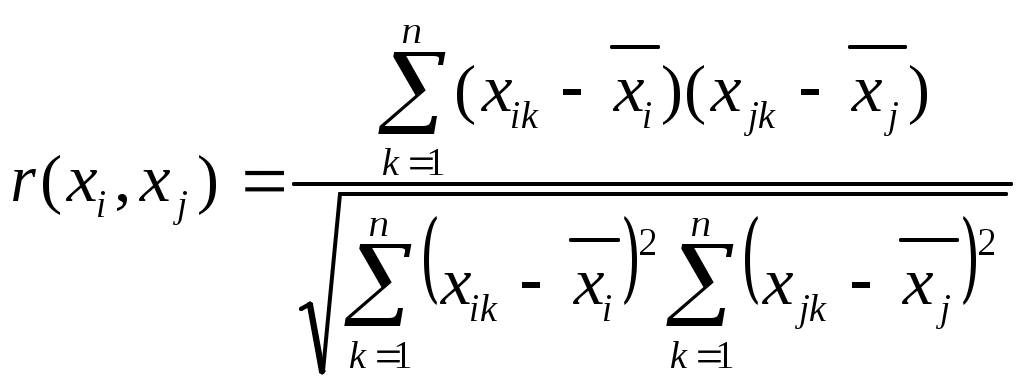 . (35)
. (35)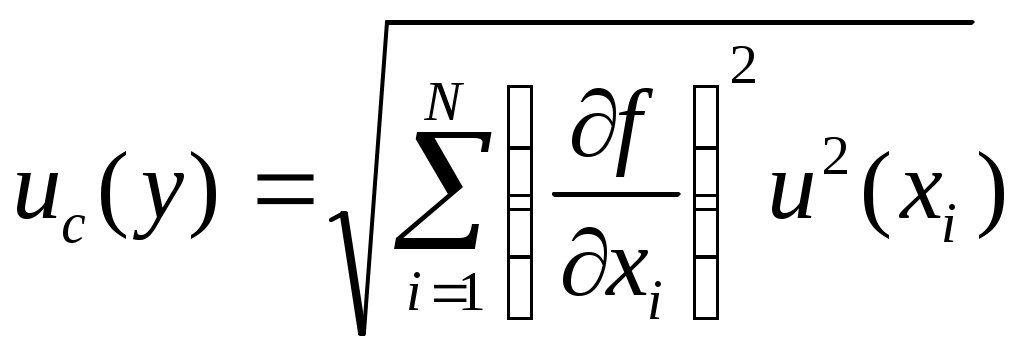 , (37)
, (37)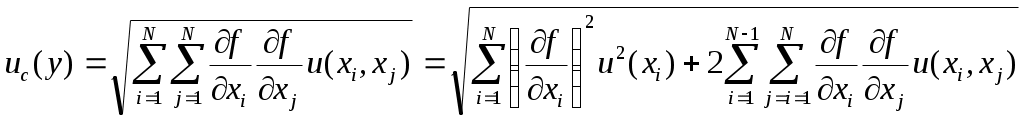 , (38)
, (38)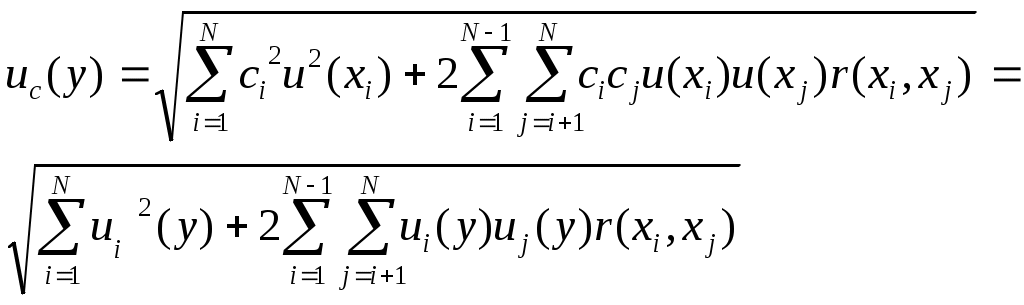 , (40)
, (40)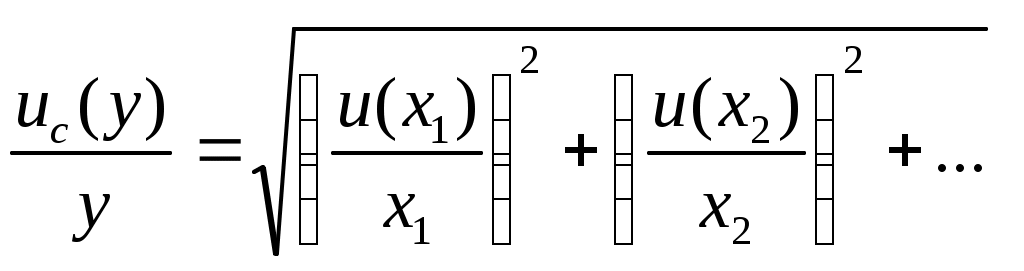 . (43)
. (43)