ЛР-16. Лабораторная работа 16

• Название: Лабораторная работа 16
• Дата: 30.03.2023
• Размер: 57.27 Kb.
• Имя файла: ЛР-16.docx
• Тип: Документы; #1025652

Лабораторная работа №16

Определение коэффициента теплопроводности твердых тел (проводников)

16.1 Цель работы

Изучить основные методы определения коэффициента удельной теплопроводности.

2. Задание

Первыйметод

1 Освоить навыки пользования измерительными приборами. 2 Собрать электрическую схему согласно рисунку 16.1.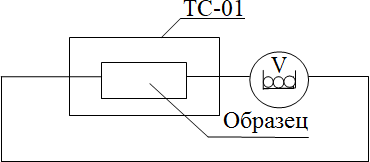


Рисунок 16.1 – Структурная схема соединения приборов и образца
3 Выписать паспортные данные приборов. 4 Измерить линейные размеры образца.

5 Выставить на термостате определенное значение температуры. 6 При заданной температуре произвести замер сопротивления R₁.

7. 
   Повторно выставить температуру Т₂ и произвести замер сопротивления R₂.
   
8. 
   Данные измерений записать в таблицу 16.1.
   

Таблица 16.1

Номер опыта	R, Ом	l, м	l1∙l2, м	σ, Ом-1∙м-1	T, К	λ, Вт/(м∙К)
1 …
12

Второйметод

1. 
   Изучить макет.
   
2. 
   Собрать электрическую схему макета (рисунок 16.2). 3 Записать паспортные данные приборов.
   

4 Измерить расстояние между термопарами.

5. 
   Установить на муфеле определенное значение температуры Т₁.
   
6. 
   Через каждые 30…60 с произвести замеры температур термоэлектрическими термометрами.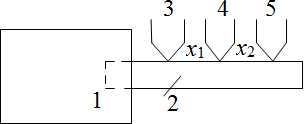
   

1 – муфель; 2 – образец; 3, 4, 5 – термопары; х₁, х₂ – расстояние между термопарами, с помощью которых можно определить температуру
Рисунок 16.2 – Структурная схема соединения приборов и образца в макете

7. 
   Выставить на муфеле значение температуры Т₂.
   
8. 
   Через каждые 30…60 с провести замеры температур термоэлектрическими приборами (термопарами).
   
9. 
   Данные измерений записать в таблицу 16.2.
   

Таблица 16.2

Номер опыта	Т1, К	Т2, К	х1, м	х2, м	Т3, К	Т4, К	λ, Вт/(м∙К)	λср, Вт/(м∙К)
1 …
12

2. Оснащение работы

Образец, термостат ТС-01, цифровой вольтметр типа В7-53, мост посто- янного или переменного тока, микроскоп МИР-2, микрометр или штангенцир- куль, секундомер.

2. Основные теоретические сведения

Первыйметод

Передача тепловой энергии от нагретого тела к менее нагретому, от нагретой части образца к менее нагретой передается различными методами, одним из которых является метод, основанный на явлении теплопроводности.

Предположим, имеется образец, в котором одна сторона имеет темпера- туру Т₁, а вторая – Т₂, причем Т₁ > Т₂, длина образца l(рисунок 16.3). В данном

случае имеется градиент температуры, т. е.

^T, поток тепловой энергии

l

ΔQ, Дж, будет направлен слева направо в образце и равен

ΔQ= λ∙Δt∙S^T,

l

где λ – коэффициент теплопроводности, Вт/(м∙с); Δt – время прохождения теплового потока, с; S– площадь cечения образца, м²;

^T– градиент температуры, К/м.

l

 Т

 l

Т₁ ^Т2
Рисунок 16.3 – Изображение потока тепла в образце
Коэффициент теплопроводности – величина, численно равная количеству тепла, протекающего через поперечное сечение в единицу времени, при единичном градиенте температуры. Поток распространяемого тепла приводит к тому, что температура образца увеличивается и образец можно характеризовать коэффициентом линейного расширения α и объемного расширения β, т. е.

α = ^l,

lT

или l_t= l(1+αΔT),

где Δl– изменение длины образца, м;

l – первоначальное значение длины образца, м; ΔТ– изменение температуры образца, К;

α – температурный коэффициент линейного расширения образца, 1/К;

l_t– длина нагретого образца, м.

_{β =} VVT

, или V_t= V(1 + βΔT),

где ΔV– изменение объема образца, м³;

V – первоначальное значение объема образца, м³; ΔТ– изменение температуры образца, м³;

β – температурный коэффициент объемного расширения образца, 1/К;

V_t– конечный объем нагретого образца, м³.

Нагреваемый образец характеризуется теплоемкостью, удельной теплоемкостью, атомной, или молярной, теплоемкостью, т. е.

С= ^Q; С_уд =

T

QmT

; С_ат =

Q_,

μT

где ΔQ – изменение тепловой энергии, Дж; ΔТ– изменение температуры, К;

m– масса образца, кг;

μ – молярная (атомная) масса данного образца, моль (n₂).

На практике необходимо определить коэффициент теплопроводности.

Существуют различные способы его определения. Рассмотрим один из них.

Согласно законам термодинамики, тепло распространяется от нагретой части к холодной и обусловлено наличием градиента dT/dx температуры. Тепловой поток переносится как электронами и ионами, так и атомами кристаллической решетки. Тепловой поток характеризуется электронной и решетчатой составляющей. Электронная составляющая на 2…3 порядка больше решетчатой составляющей теплопроводности, поэтому ею можно пренебречь.

Электроны обусловливают перенос тепла и удельную проводимость σ, Ом^–1∙м^–1:

σ = n∙e∙μ,

где n – концентрация носителей заряда – число носителей заряда в единице объема, м^–3;

e– величина заряда, Кл;

μ – подвижность носителей заряда – величина, численно равная скорости движения заряда при единичной напряженности Е= 1 В/м электронного поля, μ = U/E, м² /(В∙с).

Согласно закону Видемана – Франца, существует связь между удельной проводимостью и коэффициентом удельной теплопроводности:

λ = σ∙L₀∙Т,

где λ – численное количество, равное энергии, передаваемой образцом на единицу длины в единицу времени при градиенте температуры dT/dx = 1, при изменении температуры на 1^о, через единичную площадь, Вт/(м∙К);

σ – удельная проводимость, величина, обратная удельному сопротивлению, Ом^–1∙м^–1;


ρ 
σ  ¹ ; R^S; σ  ^{1 l};

ρ l RS

L₀ = 2,4∙10^–8 = l/3π² (k/e)² – постоянная Лоренца, В²/К²;

k– постоянная Больцмана, Дж/К;

e– величина заряда, Кл;

Т– температура образца по шкале Кельвина, К.
Второйметод

Процесс распространения тепла в твердом теле, т. е. процесс теплопроводности описывает уравнение Фурье, которое имеет следующий вид (при условии, что с, ρ, λ – постоянны в данном образце):

с∙ρ

Т(x,y,z,t) ₌

t


^ ²Т(x,y,z,t)

 λ


_ ²Т(x,y,z,t) _


²Т(x,y,z,t) ^

• 
  
  
  
  
  F,
  


^ x²

y²

x^{2 }

где с – теплоемкость образца, Дж/К; ρ – плотность образца, кг/м³;

Т(x, y, z,t)


 t

– 1-я производная по времени от температуры Тобразца, т. е.

скорость распределения температуры; λ – коэффициент теплопроводности;


^ ²Т(x,y,z,t) _


²Т(x,y,z,t)


²Т(x,y,z,t) ^

• 
  
  
  
  
  – сумма производных 2-го порядка
  


^ x²

y²

x^{2 }

по координатам;

F– потоки тепла тепловых источников.

Если для упрощения предположить, что образец имеет форму цилиндра (провода), то уравнение можно записать так:

c∙ρ∙

Т(x,t)


t

 ²Т(x,t)

= λ

х²

+ F.

После некоторых предположений и преобразований получим уравнение

Т_

t

λ


с ρ

² Т

,

х²

а после некоторых упрощений и с определенной долей достоверности – решение, которое характеризует распределение температуры вдоль образца:



Т Т₀e

λtcρx² _,

где Т– температура в искомой точке образца, К; Т₀ – температура в начальной точке образца, К; e– основание натурального логарифма.

Решая уравнение для различных соседних точек образца, получим

сρ(lnTx lnTx)

cρ  x²  x² (lnTx lnTx)

λ ¹² , или

_{λ } 1 2 1 2 _,

 _{t t} 

t₂  x²  t x²

_2 _1 _

1 1 2

 _x² _x² 

где t– время, с;

 2 1 

с – удельная теплоемкость, Дж/(кг∙град); ρ – плотность вещества, кг/м³;

х– расстояние от первоначальной точки до конечной, в которой определяется температура, м;

λ – коэффициент теплопроводности, Вт/(м∙К).

2. Порядок выполнения работы

Первыйметод

1. 
   Получить у преподавателя образец.
   
2. 
   Подсоединить исследуемый образец к клеммам крышки термостата с внутренней стороны.
   
3. 
   Вход цифрового вольтметра (измерение сопротивления) подсоединить к клеммам камеры термостата.
   
4. 
   Включить вилки приборов в сеть. 5 Включить тумблер СЕТЬ.
   

6. 
   Ручкой термостата установить нужную температуру нагрева.
   
7. 
   При данной температуре произвести измерение сопротивления образца.
   
8. 
   Выполнить измерения 12 раз и данные измерений записать в таблицу 16.1.
   

Второйметод

1. 
   Получить у преподавателя образец.
   
2. 
   Определить по справочнику удельную теплоемкость с и плотность ρ образца. Вставить образец в муфель. Привести в контакт термопары. Включить вилки приборов в сеть. Включить тумблер СЕТЬ.
   
3. 
   Включить муфель на некоторое время, определяемое секундомером. Зная расстояния х₁ и х₂ (или измерив их) и задавая температуру муфеля, получить данные, которые записать в таблицу 16.2.
   
4. 
   Через определенные промежутки времени определить значение температуры в точках 1, 2, 3.
   
5. 
   Выполнить измерения 12 раз и данные измерений и вычислений записать в таблицу 16.2.
   
6. 
   Оформить отчет по рекомендуемой форме.
   

2. Форма отчета о работе

Лабораторнаяработа№

Номеручебнойгруппы Фамилия,инициалыобучающегося Датавыполненияработы Темаработы: Цельработы: Задание: Оснащениеработы: Результатывыполненияработы:

2. Контрольные вопросы и задания

1. 
   Что такое сопротивление? Единицы измерения.
   
2. 
   Что такое удельная проводимость? Единицы измерения.
   
3. 
   
   114
   Что такое коэффициент теплопроводности? 4 Теория Друде.
   

5 Физический смысл постоянной Лоренца. 6 Что обозначает понятие «фонон»?

7 Как температура влияет на проводимость проводников?