Методичка 17 Лаба , магнетизм и электричество. Лабораторная работа 17 Исследование затухающих электрических колебаний в колебательном контуре
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
Лабораторная работа № 17Исследование затухающих электрических колебаний в колебательном контуре Приборы и принадлежности: блок колебательного контура, осциллограф, генератор импуль-сов, магазин сопротивлений, набор конденсаторов и катушек индуктивности. Цель работы:1.Изучение зависимости периода собственных колебаний от величин L и C. 2. Определение добротности и логарифмического декремента затухания. 3. Исследование влияния R на затухание колебаний и добротность контура Краткая теория 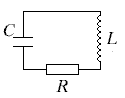 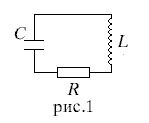 Замкнутая цепь, состоящая из емкости C, индуктивности L и активного сопротивления R, образует колебательный контур(рис.1). сопротивление R в большинстве случаев распределено между витками катушки индуктивности, между контактами, в соединительных проводах, а иногда и в конденсаторах. При относительно невысоких частотах R, L и C можно считать сосредоточенными в определенных участках цепи. Такие колебательные контуры называются колебательными системами с сосредоточенными постоянными. Замкнутая цепь, состоящая из емкости C, индуктивности L и активного сопротивления R, образует колебательный контур(рис.1). сопротивление R в большинстве случаев распределено между витками катушки индуктивности, между контактами, в соединительных проводах, а иногда и в конденсаторах. При относительно невысоких частотах R, L и C можно считать сосредоточенными в определенных участках цепи. Такие колебательные контуры называются колебательными системами с сосредоточенными постоянными.Данная работа посвящена исследованию различных колебательных процессов и измерению основных параметров колебательного контура. Рассмотрим контур, состоящий из последовательно соединенных R, L и C. Пусть в начальный момент конденсатор заряжен до разности потенциалов U Затухающие колебания напряжения на конденсаторе и тока в контуре сопровождаются процессами превращения энергии электрического поля в энергию магнитного поля и обратно. Таким образом в контуре возникнут и затухающие электромагнитные колебания, которые также условно называют просто электрическими. Электрические колебания, происходящие в колебательном контуре без воздействия внешних ЭДС, называют свободными или собственными электрическими колебаниями. Однако в зависимости от величины R, L и C разряд конденсатора в контуре может носить различный характер, который можно исследовать аналитически. Уравнение колебательного контура получим, исходя из того, что сумма падений напряжений на индуктивности, активном сопротивлении и емкости в любой момент времени равняется нулю(2-й закон Кирхгофа). Учитывая, что i= Вводя обозначение Решение этого однородного дифференциального уравнения второго порядка зависит от соотношения постоянных коэффициентов СЛУЧАЙ 1: При условии, что г 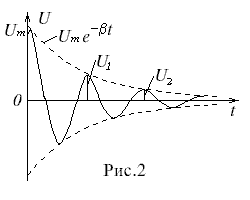 де де В контуре возникнут затухающие колебания, причем амплитуда колеба-ний изменятся по экспонен-циальному закону (рис. 2). Для характеристики колебаний вводят логарифмический декремент затухания – натуральный логарифм отношения двух амплитуд(в общем случае напряжения, заряда, тока), отстоящих друг от друга по времени на один период, например: 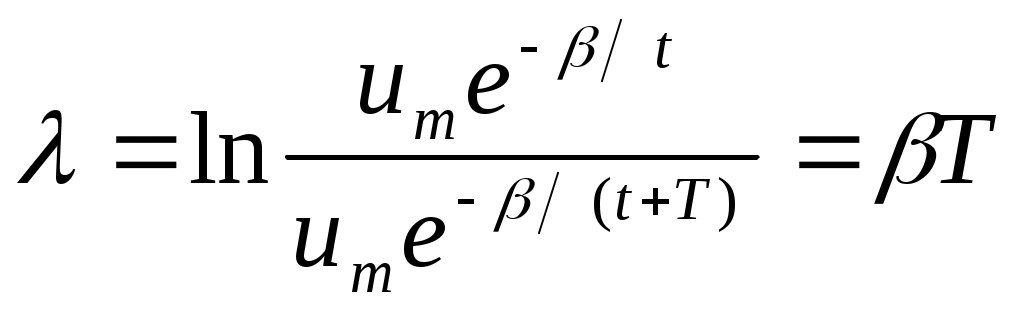 (5) (5)где Можно показать, что Колебательный контур часто удобно охарактеризовать его добротностью если затухание очень мало( Можно показать, что где W – энергия, запасенная в контуре, Отсюда видно, что добротность контура характеризует его способность сохранять запасенную энергию. Частота CЛУЧАЙ 2: При 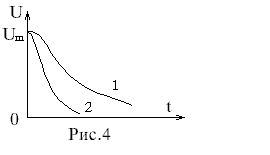 Видно, что хотя вид графика апериодического процесса зависит от начальных условий, но характерным является то, что U асимптотически приближается к нулю при t Видно, что хотя вид графика апериодического процесса зависит от начальных условий, но характерным является то, что U асимптотически приближается к нулю при t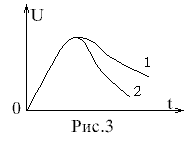 Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим. Значение критического сопротивления Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим. Значение критического сопротивления R 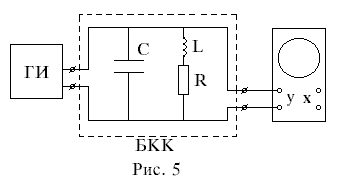 Блок-схема измерительной установки изображена на рис. 5. Для возбуждения колебаний служит генератор импульсов ГИ, присоединенный к блоку колебательного контура БКК. Колебания в контуре(напряжения на конденсаторе C) наблюдаются с помощью осциллографа ОСЦ. Генератор импульсов вырабатывает 50 раз в секунду импульсы напряжения длительностью При поступлении импульса конденсатор получает начальный заряд. В промежутке между импульсами в контуре совершаются свободные колебания. Затухание колебаний определяется в основном потерями в активном сопротивлении контура R. Шунтирующим влиянием генератора импульсов на колебательном контуре можно пренебречь. ПОРЯДОК ВЫПОЛНЕНИЯ ИЗМЕРЕНИЙ 1. Изучение зависимости периода собственных колебаний от величин L и C. а) собрать схему согласно рис. 5. выход генератора соединить с клеммами “вход” блока колебательного контура, а его “выход” – со входом осциллографа. Клеммы “R” замкнуть накоротко; б) включить генератор импульсов и осциллографа в сеть и дать им прогреться в течении 10 минут; в) снять на кальку с экрана осциллографа сигнал, вырабатываемой генератором импульсов. Для этого переключатели “L” и “C” в блоке колебательного контура поставить в положение “выкл.”, тогда выход генератора импульсов непосредственно подсоединяется к выходу осциллографа. Ручку “синхронизация” осциллографа установить в положение “от сети”. Затем управляя ручками “усиление по горизонтали” и “ослабление”, получить на экране осциллографа полное изображение двух импульсов. Устойчивость изображения добиваются вращением ручек синхронизации “диапазон частот” и “частота плавно”; Г) включить колебательный контур в схему, поставив ключи “L” и “C” в положение Д) определить период колебаний, учитывая, что расстояние между импульсами равно 0,02c ( Е) измерения проводить при разных L и C, и сравнить полученные значения с вычисленным по формуле: Значения R, L и C измеряются с помощью специального моста (например, E7-4 или I2-2). Для этого выход блока колебательного контура подсоединить ко входу моста, а генератор импульсов выключить. Так для измерения емкости C ключ “L” поставить в положение “выкл.”, а ключ “C” поочередно в положение Ж) результаты измерений представляют в виде: -осциллограмма с указанием значений L, R и C, при котором они получены; -графиков зависимости T=f(C) при L=const и R=const; T=f(L) при C=const и R= const. 2. Определение добротности и логарифмического декремента затухания а) определить логарифмический декремент затухания б) вычислить добротность контура, используя формулу в) определить г) результаты предоставить в виде таблиц значений 3. Исследование влияния R на затухание колебаний и добротность контура а) подключить к клеммам “R” магазин сопротивлений типа P-33, проследить на экране осциллографа переход колебательной формы разряда конденсатора в апериодически с ростом активного сопротивления; б) снять осциллограммы на кальку и измерить период колебаний при различных значениях R для данных значений L и C; в) определить критическое сопротивление исследуемого контура г) сравнить эти значения с вычисленными по (8) из условия: д) изучить влияние активного сопротивления контура на его добротность и сравнить с вычисленным по формуле (6); е) результаты исследований представить в виде таблиц значений (экспериментальные и теоретические) при различных L и C и графика КОНТРОЛЬНЫЕ ВОПРОСЫ -дайте определение собственных (свободных) колебаний; -назовите способы возбуждения электрических колебаний в контуре. Как влияет способ возбуждения (начальные условия) на колебательный процесс? -дайте определение колебательного контура и его основных параметров; -какое сопротивление называется критическим? -как экспериментально определяются период колебаний и добротность контура в данном упражнении? Предложите какой-нибудь другой способ определения T и -решите дифференциальное уравнение (1) и проанализируйте полученное решение. ЛИТЕРАТУРА: Калашников С. Г. Электричество. М.: 1977, ст. 207-210. Савельев И. В. Курс общей физики. М.: 1973, т.2, 99,100. Технические описания к осциллографу и измерительному мосту. ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Исследование затухающих электрических колебаний в колебательном контуре Лабораторная работа по электричеству № 17для студентов 2 курса физического факультета Уфа РИЦ БашГУ 2009 Печатается по решению кафедры общей физики: Протокол № от 15 октября 2009 г. Составители: д.ф.-м. н., проф. Альмухаметов Р.Ф. к.ф.-м. н., доц. Гафуров И.Г. |
