Лабораторная работа 2 Изучение относительного покоя жидкости при вращательном движении Вариант 5
 Скачать 411.85 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования Волжский государственный университет водного транспорта Кафедра водных путей и гидротехнических сооружений Лабораторная работа № 2 «Изучение относительного покоя жидкости при вращательном движении» Вариант №5 Выполнил Студент ОСМ-312 Силкин Д.А. Проверил Ст. Преподаватель Никитаев И.В. Н.Новгород 2021 2.1 Описание физического процесса л/р № 2. В работе рассматривается случай, когда жидкость, находящаяся в открытом цилиндрическом сосуде, вращается вместе с ним с постоянной угловой скоростью ω вокруг его вертикальной оси. Дело в том, что стенки вращающегося цилиндра благодаря силам трения сначала приводят во вращение ближайшие к ним слои жидкости, а затем, вследствие вязкости жидкости, и всю ее массу. Таким образом, через некоторое время все частицы жидкости начинают вращаться с той же угловой скоростью ω, что и стенки, т. е. вся масса жидкости относительно вращающегося цилиндра будет неподвижна (будет находиться в относительном покое). В этом случае на каждую частицу жидкости действуют две массовые силы: сила тяжести, создающая ускорение g=9,81 м/с 2 , и центробежная сила, создающая ускорение ω2 r. Здесь r – радиус вращения частицы на свободной поверхности; ω = πn/30 – угловая скорость вращения сосуда, с–1, где n – частота вращения сосуда, об/мин. Благодаря действию центробежных сил свободная поверхность вращающейся жидкости в цилиндрическом сосуде принимает форму параболоида вращения. Кривая, образующаяся от пересечения этого параболоида с вертикальной плоскостью, представляет собой квадратичную параболу (рис. 2.1). Для рассматриваемого в работе случая относительного покоя закон распределения гидростатического давления р в жидкости (основное уравнение гидростатики) имеет вид  Разделив уравнение (2.1) на ρ g и перенеся p0 в левую часть, получим выражение (2.2) для определения заглубления h рассматриваемой точки вращающейся жидкости под свободную поверхность: 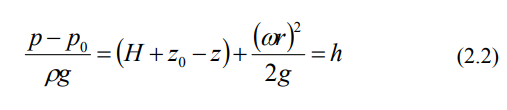 Где  – превышение точки свободной поверхности, расположенной на расстоянии r от оси вращения, над вершиной О’ параболоида вращения. С учетом выражений для h и a закон распределения гидростатического давления во вращающейся жидкости (2.1) принимает такой же вид, как и для случая абсолютного покоя, а именно: Уравнение свободной поверхности вращающейся жидкости, полученное из уравнения (2.2), при p = p0 = patm имеет вид  При r=R (здесь R – внутренний радиус цилиндра) из уравнения (2.4) получаем выражение для определения высоты H параболоида вращения:  Зависимость (2.4) лежит в основе работы жидкостных тахометров – приборов для измерения числа оборотов вала различных машин. А само явление относительного равновесия жидкости во вращающемся цилиндре используется, например, при центробежном литье труб. 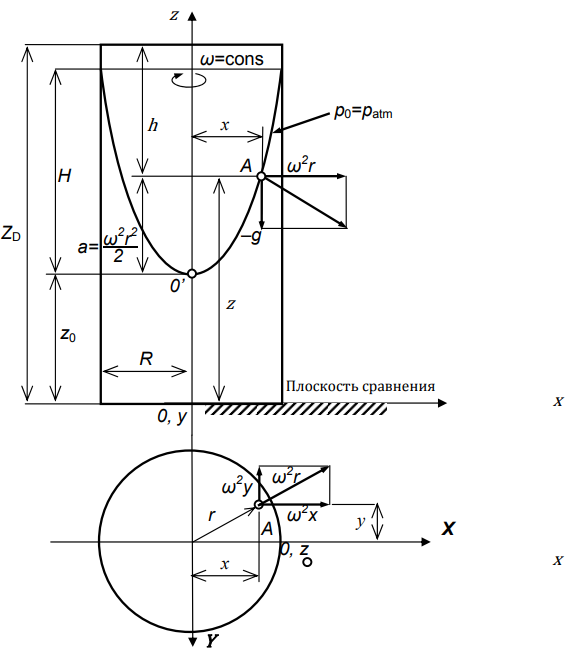 Рисунок 2.1– К относительному покою жидкости во вращающемся цилиндрическом сосуде 2.2. Описание лабораторной установки № 2. Схема установки для изучения относительного покоя жидкости, представлена на рис. 2.2. Симуляционная модель лабораторной установки (рис. 2.3) включает открытый вертикальный цилиндрический сосуд с водой (1), установленный на вращающуюся платформу (2). Платформа соединена с помощью вала (3) с электродвигателем в нижней части установки. Электродвигатель включается с помощью тумблера (4). Регулятор (5) позволяет изменять скорость вращения платформы. Текущие обороты вала отслеживаются с помощью тахометра (6). Для определения координат x и z точек свободной поверхности вращающейся жидкости установка снабжена горизонтальной линейкой (8) и вертикальной мерной иглой (7), являющейся уровнемером, позволяющей точно фиксировать высотное положение точек свободной поверхности. Касание иглы и свободной поверхности жидкости отслеживается с помощью увеличенной области на экране (9). 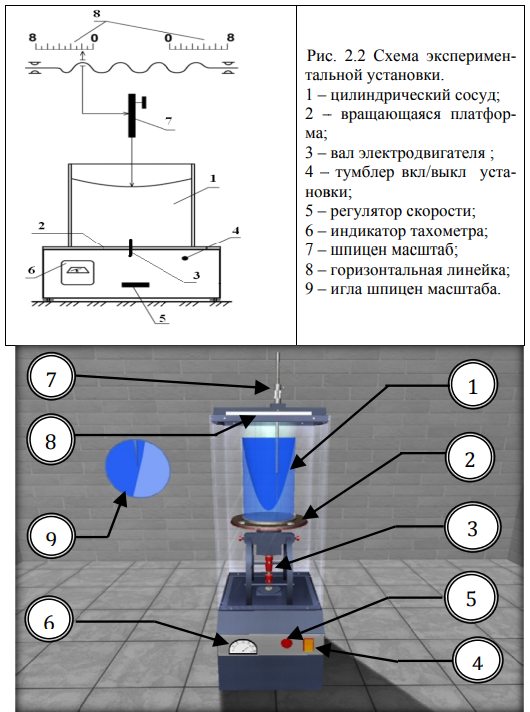 Рисунок 2.3 Симуляционная модель лабораторной установки 2.3. Порядок выполнения л/р № 2. Цели лабораторной работы: 1. Пронаблюдать процесс установления равновесия воды в открытом цилиндре, вращающемся с постоянной угловой скоростью ω вокруг вертикальной оси, обратив при этом особое внимание на характер свободной поверхности; измерить координаты x и z пяти ее точек, расположенных от оси вращения на расстояниях x, равных 1,00 R; 0,75 R; 0,50 R; 0,25 R и 0,00R, радиуса цилиндра. 2. Измерить на установке высоту параболоида вращения Hexp, сравнить ее с теоретической H, вычисленной по формуле (2.5), и определить относительное отклонение. 3. Построить по опытным данным в масштабе параболоид вращения и две эпюры манометрического давления (по глубине жидкости, на расстоянии R от оси вращения и по дну цилиндра). Результаты измерений и вычислений
Результаты вычисления для построения эпюры
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
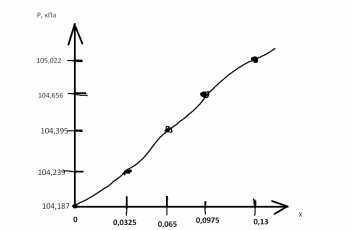