Определение достоверности отличий. Отчёт ЛР №2. Лабораторная работа 2. Определение достоверности отличий
 Скачать 21.85 Kb.
|
|
Лабораторная работа №2. Определение достоверности отличий Цель работы – научиться определять достоверности отличий на основании критерия Стьюдента и Хи-квадрата. Ход работы: Задание 1: По предложенной ниже таблице необходимо заполнить данные по 100 спортсменам в каждой группе и каждого пола при помощи функции случайного числа.
Функция СЛУЧМЕЖДУ возвращает целые числа в указанном интервале. Для того, чтобы получить нужные нам числа, необходимо использовать формулу. Например, для заполнения массы тела в интервале 78,8-89,4 формула выглядит следующим образом «=СЛУЧМЕЖДУ(788;894)/10». Задание 2: Определить достоверность различия между группами спортсменов 1 и 2 группы мужчин и первой группы мужчин и женщин. Среднее значение (Хс, М) – центр выборки, вокруг которого группируются элементы выборки. Посчитайте среднее значение для каждой группы больных с использованием статистических функций СРЗНАЧ. (Вставка функция (fx); категория Статистические). Стандартное отклонение (среднее квадратическое отклонение) – параметр, характеризующий степень разброса элементов выборки от среднего значения. Чем больше среднее квадратичное отклонение, тем дальше отклоняются значения элементов выборки от среднего значения. Обозначается «» (сигма). (Вставка функция, Статистические, СТАНДОТКЛОН). Сопоставляем средние значения массы тела первой группы спортсменов (83,92) и второй (52,87), они отличаются. Однако по этим данным делать выводы нельзя. Для решения задачи использует критерий различия: критерий Стъюдента (t). Полученное значение сравнивается с уровнем значимости (0,05). Если t меньше уровня значимости, значит нулевая гипотеза отвергается. Первоначально нам надо выдвинуть нулевую гипотезу. Поскольку мы хотим доказать достоверность различий между группами, значит нулевую гипотезу выдвигаем как утверждение обратное тому, что мы хотим доказать Нулевая гипотеза: средние равны между собой, следовательно отличие в параметре двух групп является случайным. Для вычисления критерия Стъюдента установить курсор в ячейку ниже заполненных ячеек. Меню Вставка функция,в появившемся окне Мастер функций выбрать категорию Статистические и функцию ТТЕСТ. В появившееся диалоговое окно указателем мыши ввести диапазон данных контрольной группы в поле Массив1 (D10:E109), в поле Массив2 ввести диапазон данных исследуемой группы (D117:E216), в поле Хвосты вводится число хвостов распределения – 2, т.к. мы предполагаем, что распределение является двусторонним; в поле Тип с клавиатуры ведите 3 (т.к. у нас две разные группы лиц и дисперсия (стандартное отклонение) – не равны). Enter. Получили результат =  .Вывод: Сравниваем полученное значение с уровнем значимости (0,05). Значение ТТЕСТ (т.е. величина вероятности того, что две выборки взяты из одной генеральной совокупности) = меньше уровня значимости, следовательно, нулевая гипотеза отвергается. Значит различие между выборками не случайные и средние выборок считаются достоверно отличающимися друг от друга.Задание 3: Определить, влияет ли число заявок в месяц на продуктивность работы техника АСОИУ (отсутствие необслуженных заявок).
Нулевая гипотеза: число заявок в месяц не влияет на продуктивность работы техника АСОИУ. После выдвижения нулевой гипотезы определяется ожидаемое значение результата. Обычно это среднее значение между выборками. В примере (90+10)/2=50, т. е. мы ожидали, что разницы между группами нет и в обоих случаях число заявок должно составить 50. Затем вычисляется значение вероятности того, что изучаемые события (необслуженные заявки в обеих выборках) произошли случайным образом. Для этого вводим данные в рабочую таблицу: 10 — в ячейку D229, 90 — в E229, 50 — в D230 и E230. Табличный курсор устанавливается в свободную ячейку (ЕЗ). На панели инструментов необходимо нажать кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер функций выбрать категорию Статистические и функцию ХИ2-ТЕСТ, после чего нажать кнопку ОК. Появившееся диалоговое окно ХИ2ТЕСТ за серое поле мышью отодвинуть вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши ввести диапазон данных наблюдавшейся заболеваемости в поле Фактический интервал (D229:E229). В поле Ожидаемый интервал ввести диапазон данных предполагаемой заболеваемости (D230:E230). Нажать кнопку ОК. В ячейке ЕЗ появится значение вероятности - 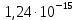 .Вывод: Поскольку величина вероятности случайного появления анализируемых выборок ( 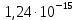) меньше уровня значимости (р=0,05), то нулевая гипотеза отвергается. Следовательно, различия между выборками не могут быть случайными и выборки считаются достоверно отличающимися друг от друга. Поэтому на основании применения критерия хи-квадрат можно сделать вывод о том, что число заявок в месяц влияет на продуктивность работы техника АСОИУ. Выводы: в ходе выполнения работы были закреплены навыки определения достоверности отличий на основании критерия Стьюдента и Хи-квадрата. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||