2 физ. Лабораторная работа 2 Свободные колебания, их основные характеристики. Основы взаимодействия ультразвука с биологическими объектами

• Название: Лабораторная работа 2 Свободные колебания, их основные характеристики. Основы взаимодействия ультразвука с биологическими объектами
• Дата: 25.12.2022
• Размер: 372.76 Kb.
• Имя файла: 2 физ.docx
• Тип: Лабораторная работа; #862516

Лабораторная работа 2

«Свободные колебания, их основные характеристики. Основы взаимодействия ультразвука с биологическими объектами»

Цель работы:

1. 
   Научиться регистрировать простейшие колебательные процессы.
   
2. 
   Научиться определять основные параметры колебаний.
   

Задачи:

1. 
   Изучить известные виды колебаний и установить взаимосвязь между их базовыми параметрами.
   
2. 
   Проанализировать уравнения, описывающие колебательные движения.
   
3. 
   Провести исследование свободных колебаний на примере электрического контура.
   
4. 
   Рассчитать данные, описывающие колебательные движения, и сделать выводы о полученных результатах.
   

Литература:

1. 
   Ремизов, А. Н. Медицинская и биологическая физика : учебник / А. Н.
   

Ремизов. - 4-е изд. , испр. и перераб. - Москва : ГЭОТАР-Медиа, 2016. - 656 с. - ISBN 978-5-9704-3577-9. - Текст : электронный // ЭБС "Консультант студента" :

[сайт]. - URL : https://www.studentlibrary.ru/book/ISBN9785970435779.html

2. 
   Антонов, В. Ф. Физика и биофизика: учебник / В. Ф. Антонов, Е. К.
   

Козлова, А. М. Черныш. - 2-е изд., испр. и доп. - Москва : ГЭОТАР-Медиа,

2015. - 472 с. - ISBN 978-5-9704-3526-7. - Текст : электронный // ЭБС

"Консультант студента" : [сайт]. - URL: https://www.studentlibrary.ru/book/ISBN9785970435267.html

Приборы и принадлежности:

1. 
   Scilab — пакет прикладных математических программ;
   
2. 
   Персональный компьютер.
   

2.Практическая часть:

Моделирование механических колебаний.

Задание 1. Моделирование гармонического колебания.

Произвести моделирование гармоническое колебание с помощью пакета прикладных математических программ Scilab. Рассчитать Т, θ.

Уравнение гармонического колебания имеет вид: х = 𝐴sin(𝜔₀𝑡 + 𝜑) – для нечетных по списку студентов х = 𝐴cos(𝜔₀𝑡 + 𝜑) - для четных по списку студентов

Данные для моделирования представлены в таблице 1.

Таблица 1.

№ п.п.	А, амплитуда, мВ	ⅴ, частота, Гц	φ - начальная фаза колебаний	Т – период колебаний, с	𝜃 = 𝜔0𝑡+𝜑 – фаза колебаний в момент времени t	t - момент времени, с
1	3	1	0	1	6,28;12,56;25,12	1;2;4
2	5	2	30			1,2,4
3	7	3	45	0.33	73,26 ; 109,056;142,968	1,5;3,4;5,2
4	9	5	60			2,1;3;4,4
5	12	7	90	0.143	133,96;185,2;265,84	1,2,4
6	13	9	0			1,5;3,4;5,2
7	15	10	30	0,1	161,88;218,4;306,32	2,1;3;4,4
8	17	11	45			1,7;5;9,5
9	20	12	60	0,083	218,256; 286,08; 391,584	2,1;3;4,4
10	22	14	80			1,2,4

x. = A.*sin(𝜔𝑡 + 𝜑);

t=0:0.01:10

x=0.003*sin(2*%pi*1*t+0)

plot2d(t,x)

A= [3 5 7];

v= [1 2 3];

φ= [0 30 45];

В результате выполнения задания представьте график и листинг моделирования гармонических колебаний с помощью пакета прикладных математических программ Scilab. Рассчитать Т, θ. Рассчитайте значение х(t) при заданных t, отметьте на графике. Запишите вывод по результатам анализа данных. Сделайте вывод по заданию.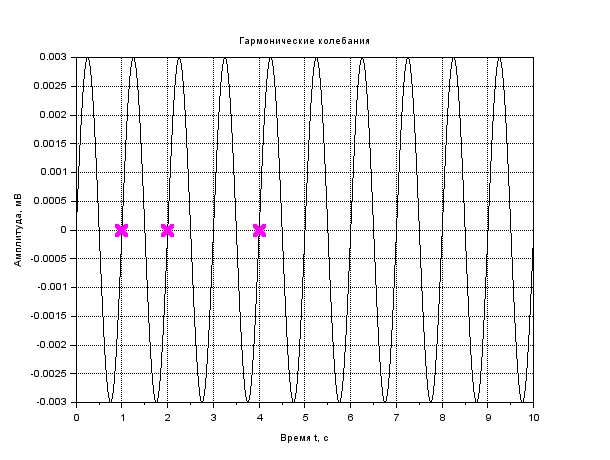



Рисунок 1- Гармонические колебания

Листинг :

t=0:0.01:10

A=0.003 //Амплитуда

n=1 //Частота

fi=0 //Начальная фаза колебаний

x=A*sin(2*%pi*n*t+fi)

t1=1

t2=2

t3=4

plot(t,x,'k')

xtitle('Гармоническиеколебания','Времяt, c','Амплитуда, мВ')

xgrid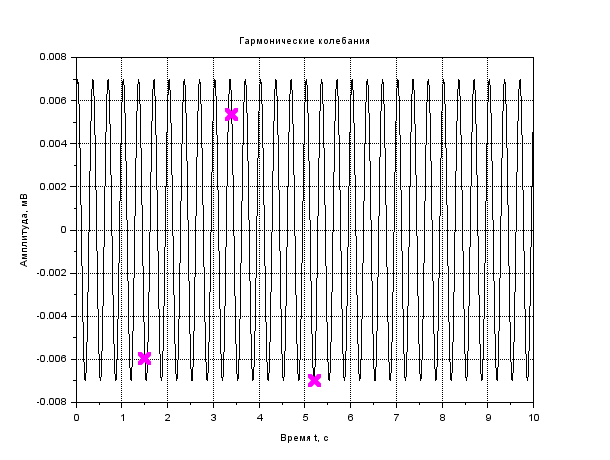



Рисунок 2- Гармонические колебания

Листинг :

t=0:0.01:10

A=0.007 //Амплитуда

n=1 //Частота

fi=0 //Начальная фаза колебаний

x=A*sin(2*%pi*n*t+fi)

t1=1,5

t2=3,4

t3=5,2

plot(t,x,'k')

xtitle('Гармоническиеколебания','Время t, c','Амплитуда, мВ')

xgrid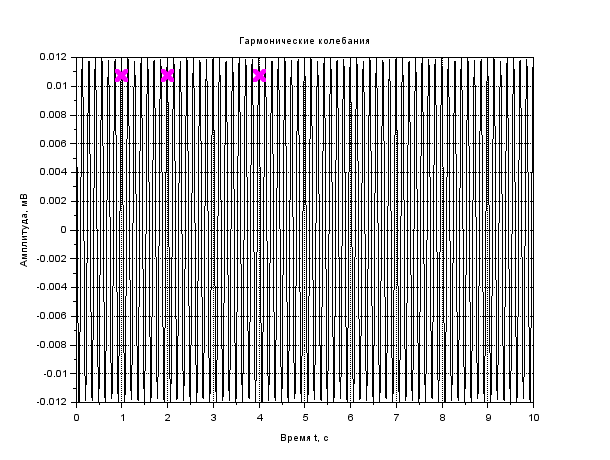



Рисунок 3- Гармонические колебания

Листинг

t=0:0.01:10

A=0.012 //Амплитуда

n=1 //Частота

fi=0 //Начальная фаза колебаний

x=A*sin(2*%pi*n*t+fi)

t1=1

t2=2

t3=4

plot(t,x,'k')

xtitle('Гармоническиеколебания','Времяt, c','Амплитуда, мВ')

xgrid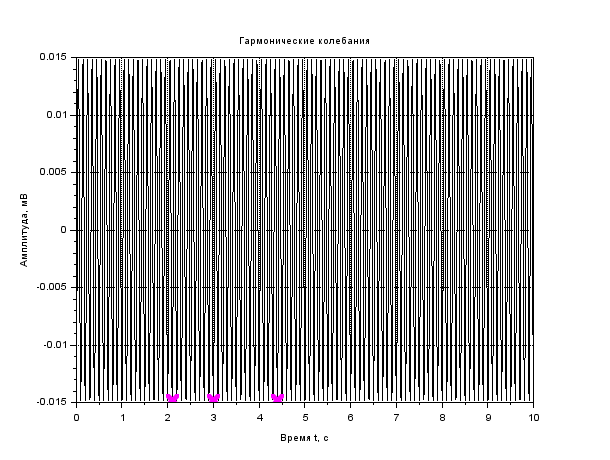



Рисунок 4- Гармонические колебания

Листинг

t=0:0.01:10

A=0.015 //Амплитуда

n=1 //Частота

fi=0 //Начальная фаза колебаний

x=A*sin(2*%pi*n*t+fi)

t1=2,1

t2=3

t3=4,4

plot(t,x,'k')

xtitle('Гармоническиеколебания','Время t, c','Амплитуда, мВ')

xgrid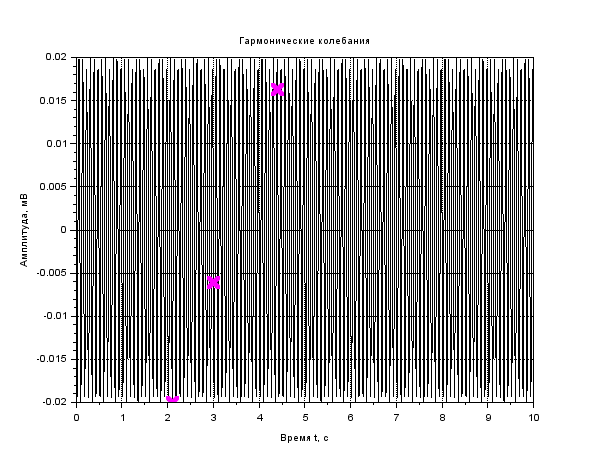



Рисунок 5-Гармонические колебания

Листинг

t=0:0.01:10

A=0.02 //Амплитуда

n=1 //Частота

fi=0 //Начальная фаза колебаний

x=A*sin(2*%pi*n*t+fi)

t1=2,1

t2=3

t3=4,4

plot(t,x,'k')

xtitle('Гармоническиеколебания','Время t, c','Амплитуда, мВ')

xgrid

Вывод : чем больше амплитуда ,тем больше частота колебаний ,при этом период колебаний уменьшается. С увеличением времени увеличивается фаза колебаний.

Задание 2. Моделирование свободных затухающих колебаний.

Произвести моделирование затухающего колебания с помощью пакета прикладных математических программ Scilab.

Уравнение свободных затухающих колебаний имеет вид:

𝑥(𝑡) = 𝐴𝑒^−𝛽𝑡cos(𝜔𝑡 + 𝜑₀)

Данные для моделирования представлены в таблице 2.

Таблица 2.

№ п.п.	А, амплитуда, мВ	ⅴ, частота, Гц	φ - начальная фаза колебаний	𝛽 - показатель затухания	Т – период колебаний, с	𝜃 = 𝜔0𝑡+ 𝜑 – фаза колебаний в момент времени t	t - момент времени, с
1	3	1	0	0,1	1	6,28;12,56;25,12	1;2;4
2	5	2	30	0,13			1,2,4
3	7	3	45	0,25	0,33	73,26 ; 109,056;142,968	1,5;3,4;5,2
4	9	5	60	0,3			2,1;3;4,4
5	12	7	90	0,4	0,14	133,96;185,2;265,84	1,2,4
6	13	9	0	0,44			1,5;3,4;5,2
7	15	10	30	0,5	0,1	161,88;218,4;306,32	2,1;3;4,4
8	17	11	45	0,6			1,7;5;9,5
9	20	12	60	1	0,083	218,256; 286,08; 391,584	2,1;3;4,4

В результате выполнения задания представьте график и листинг моделирования гармонических колебаний с помощью пакета прикладных математических программ Scilab. Рассчитать Т, θ, λ, τ, 𝑁_𝑒. Запишите вывод по результатам анализа данных. Сделайте вывод по заданию.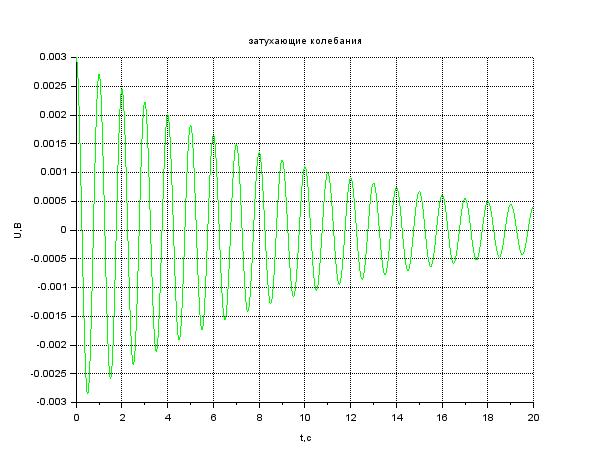



Рисунок 1. График затухающих колебаний 1

Листинг :

//затухающие колебания

t=0:0.01:20

f=1//частота

w=2*%pi*f

A=0.003*exp(-t*0.1)

x=A.cos(w*t+0)

plot2d(t,x,7)

xgrid()

xtitle('затухающиеколебания')

xlabel('t,c')

ylabel('U,B')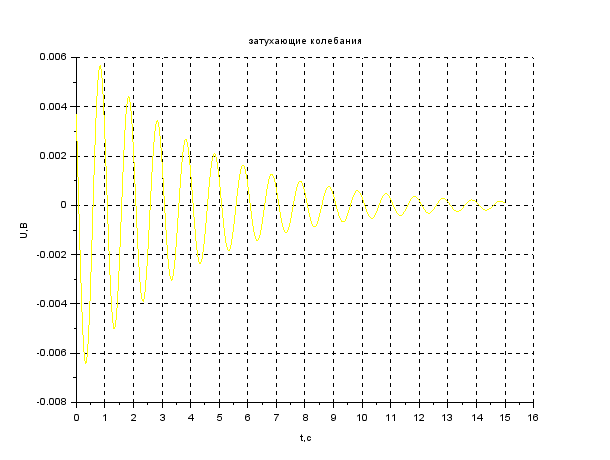



Рисунок 2. График затухающих колебаний 3

Листинг :

//затухающие колебания

t=0:0.01:15

f=1//частота

w=2*%pi*f

A=0.007*exp(-t*0.1)

x=A.cos(w*t+0)

plot2d(t,x,3)

xgrid()

xtitle('затухающиеколебания')

xlabel('t,c')

ylabel('U,B')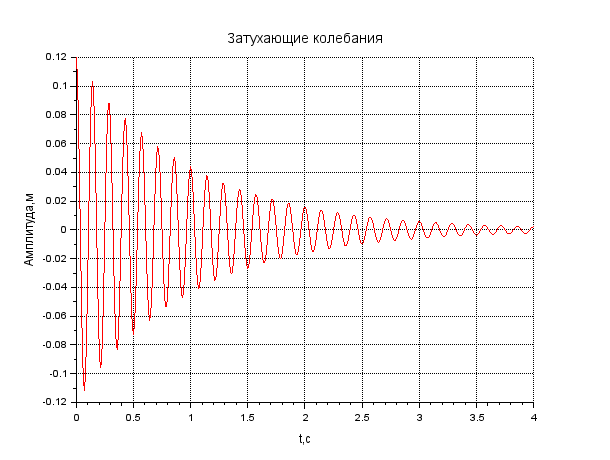



Рисунок 3. График затухающих колебаний 5

Листинг

//затухающие колебания

t=0:0.01:4

f=1//частота

w=2*%pi*f

A=0.012*exp(-t*0.1)

x=A.cos(w*t+0)

plot2d(t,x,5)

xgrid()

xtitle("Затухающиеколебания")

xlabel("t,c")

ylabel("Амплитуда,м")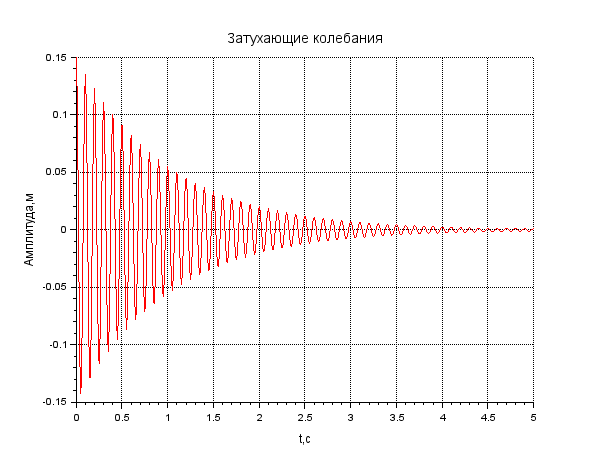



Рисунок 4. График затухающих колебаний 7

Листинг

//затухающие колебания

t=0:0.01:5

f=1//частота

w=2*%pi*f

A=0.015*exp(-t*0.1)

x=A.cos(w*t+0)

plot2d(t,x,5)

xgrid()

xtitle("Затухающиеколебания")

xlabel("t,c")

ylabel("Амплитуда,м")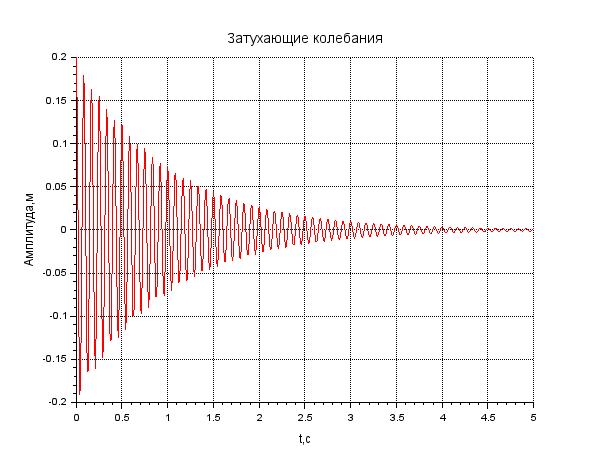



Рисунок 5. График затухающих колебаний 9

Листинг

//затухающие колебания

t=0:0.01:5

f=1//частота

w=2*%pi*f

A=0.02*exp(-t*0.1)

x=A.cos(w*t+0)

plot2d(t,x,5)

xgrid()

xtitle("Затухающиеколебания")

xlabel("t,c")

ylabel("Амплитуда,м")

Вывод:Во всякой реальной колебательной системе имеются силысопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать.И чем больше будут амплитуда, частота, и показатель затуханий, тем быстрее будут затухать колебания, то есть период колебаний будет становиться меньше.

Задание 3. Затухание ультразвука в биологических тканях

Произвести моделирование затухающего колебания с помощью пакета прикладных математических программ Scilab.

Плоская волна в однородной среде затухает в основном в результатете поглощения ультразвука.

Амплитуда колебания частиц уменьшается с расстоянием х в соответствии с уравнением:

𝐴 = 𝐴0𝑒−𝛼𝑥

Интенсивность ультразвука уменьшается с расстоянием х в соответствии с уравнением:

𝐼 = 𝐼₀𝑒−2𝛼𝑥

где 𝐴₀, 𝐼₀ – амплитуда колебания частиц и интенсивность ультразвука

вблизи источника;

𝐴, 𝐼 - амплитуда колебания частиц и интенсивность ультразвука на расстоянии х от источника; α – коэффициент поглощения; е – основание натурального логарифма, число Непера (е ≈ 2,72) Данные для моделирования представлены в таблице 3.

Таблица 3.

№ п.п.	ткань	скорость ультразвука, м/с	Акустическое сопртивление, кг/м2с	ⅴ, частота, МГц	𝐼0 - интенсивно сть ультразвук а вблизи источника, Вт/см2	α – коэффициен т поглощения, дБ/см, при f = 1МГц	х – расстояние, см
1	кровь	1570	1,61	1	0,5	0,13	0,1;0,2
2	мозг	1541	1,58	1	0,5	0,85	0,5;0,7
3	жир	1450	1,38	1	0,5	0,63	0,5;0,8
4	почка	1561	1,62	1	0,5	1	0,5
5	печень	1549	1,65	1	0,5	0,94	0,5
6	мышца: вдоль фибрил л поперек фибрил	1585 - -	1,70 - -	1	0,5	1,30 3,30	0,5
7	кости черепа	4080		1	0,5	13	0,1;0,2
8	вода	1480		1	0,5	0,0022	0,5;1

В результате выполнения задания:

• 
  рассчитать 𝐴₀ - амплитуда колебания частиц вблизи источника;
  
• 
  рассчитать⁡𝐴, 𝐼 - амплитуда колебания частиц и интенсивность ультразвука на расстоянии х от источника;
  
• 
  рассчитать λ - логарифмический декремент затухания;
  
• 
  рассчитать v- амплитуду скорости колеблющихся частиц;
  
• 
  рассчитать а – колебательное ускорение;
  

- расчитать Т – период колебаний.

Представьте график и листинг моделирования амплитуды колебания частиц от расстояния х, интенсивности ультразвука от расстояния х для различных тканей.

Рассчитать какую деформацию испытывает эритроцит при данных условиях.

№	Ткань	A0,мкм	A, мкм	I, Вт/см2	λ	ⅴ	a	T
1	Кровь	12,55	12,39 12,23	0,49 0,47	1,3*10-7	0,78 0,76	4,9*106 4,8*106	10-6
2	Мозг	12,68	8,29 6,99	0,21 0,15	8,5*10-7	0,52 0,46	3,24*106 2,8*106	10-6
3	Жир	13,56	9,9 8,19	0,27 0,18	6,3*10-7	0,63 0,51	3,9*106 3,2*106	10-6
4	Почка	12,51	7,59	0,18	1*1010-6	0,47	2,9*106	10-6
5	Печень	12,4	7,75	0,2	9,4*10-7	0,49	3,09*106	10-6
6	Мышца: Вдоль фибрилл Поперек фибрилл	12,21	6,37 2,34	0,14 0,02	1,3*10-6 3,3*10-6	0,41 0,15	2,5*106 9,6*105	10-6
7	Кости черепа	5,7	1,55 0,42	0,037 0,003	1,3*10-5	0,097 0,028	6,1*105 1,7*105	10-6
8	вода	13,09	13,076 13,061	0,499 0,498	2,2*10-10	0,8218 0,8203	5,16*106 5,15*106	10-6

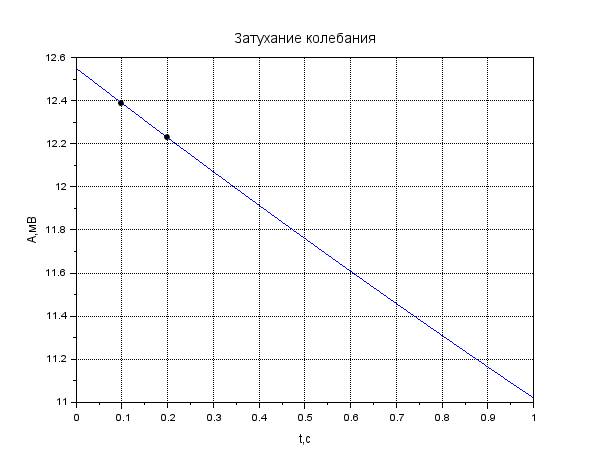Рисунок 1. Затухание амплитуды в крови.

Листинг:

x=0:0.01:1//Расстояние от источника

A0=12.55//Амплитуда вблизи источника

a=0.13//Коэффицентпоглощения

A=A0*exp(-a*x);

xgrid()

xtitle("Затуханиеколебания","t,сек","A,мВ")

xlabel('t,c');

ylabel('A,мВ')

plot(x,A,2);

x=[0.1,0.2];

plot(x,A=A0*exp(-a*x),'k.');

xgrid()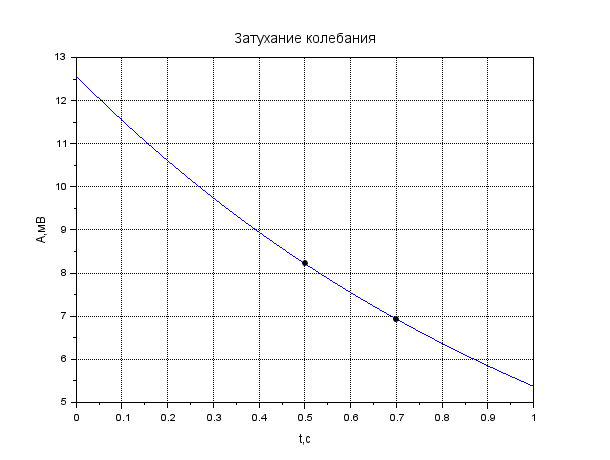



Рисунок 2. Затухание амплитуды в мозге.

Листинг:

x=0:0.01:1//Расстояние от источника

A0=12.57//Амплитуда вблизи источника

a=0.85//Коэффицентпоглощения

A=A0*exp(-a*x);

xgrid()

xtitle("Затуханиеколебания","t,сек","A,мВ")

xlabel('t,c');

ylabel('A,мВ')

plot(x,A,2);

x=[0.5,0.7];

plot(x,A=A0*exp(-a*x),'k.');

xgrid()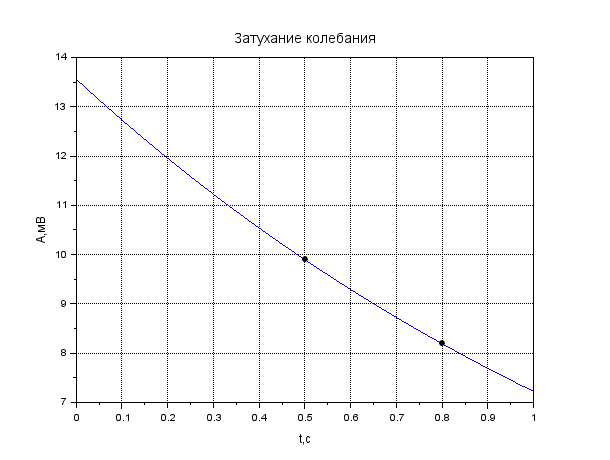



Рисунок 3. Затухание колебания в жире.

Листинг:

x=0:0.01:1//Расстояние от источника

A0=13.56//Амплитуда вблизи источника

a=0.63//Коэффицентпоглощения

A=A0*exp(-a*x);

xgrid()

xtitle("Затуханиеколебания","t,сек","A,мВ")

xlabel('t,c');

ylabel('A,мВ')

plot(x,A,2);

x=[0.5,0.8];

plot(x,A=A0*exp(-a*x),'k.');

xgrid()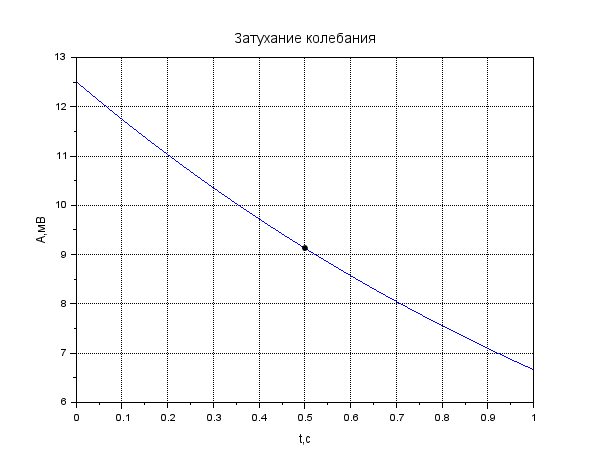



Рисунок 4. Затухание колебания в почке.

Листинг:

x=0:0.01:1//Расстояние от источника

A0=12.51//Амплитуда вблизи источника

a=0.63//Коэффицентпоглощения

A=A0*exp(-a*x);

xgrid()

xtitle("Затуханиеколебания","t,сек","A,мВ")

xlabel('t,c');

ylabel('A,мВ')

plot(x,A,2);

x=[0.5];

plot(x,A=A0*exp(-a*x),'k.');

xgrid()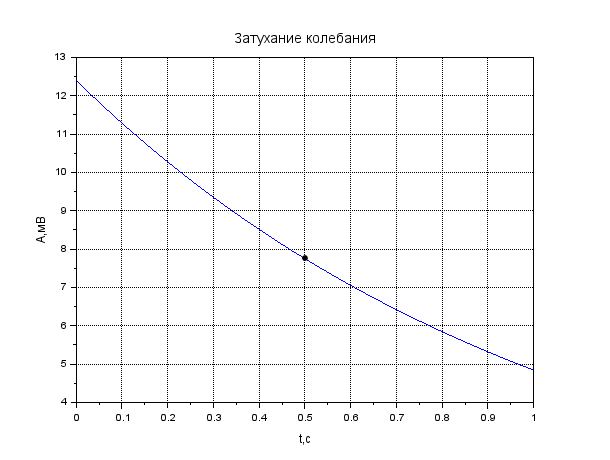


Рисунок 5. Затухание колебания в печени

Листинг:

x=0:0.01:1//Расстояние от источника

A0=12.4//Амплитуда вблизи источника

a=0.94//Коэффицентпоглощения

A=A0*exp(-a*x);

xgrid()

xtitle("Затуханиеколебания","t,сек","A,мВ")

xlabel('t,c');

ylabel('A,мВ')

plot(x,A,2);

x=[0.5];

plot(x,A=A0*exp(-a*x),'k.');

xgrid()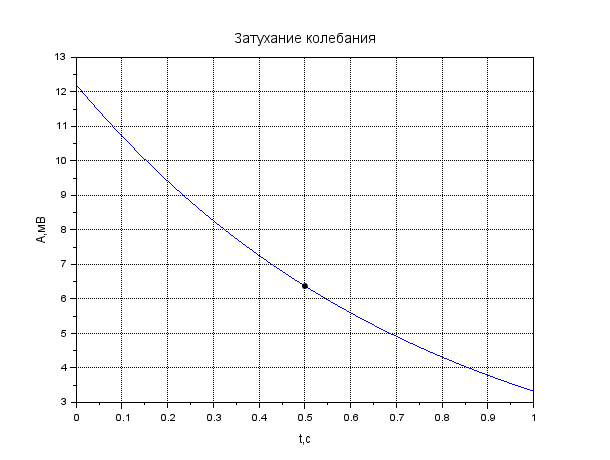



Рисунок 6. Затухание колебания в мышце вдоль фибрилл.

Листинг:

x=0:0.01:1//Расстояние от источника

A0=12.21//Амплитуда вблизи источника

a=1.3//Коэффицентпоглощения

A=A0*exp(-a*x);

xgrid()

xtitle("Затуханиеколебания","t,сек","A,мВ")

xlabel('t,c');

ylabel('A,мВ')

plot(x,A,2);

x=[0.5];

plot(x,A=A0*exp(-a*x),'k.');

xgrid()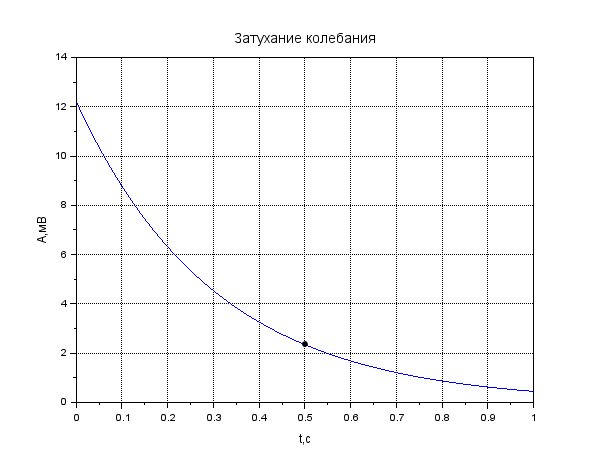



Рисунок 7. Затухание колебания в мышце поперек фибрилл.

Листинг:

x=0:0.01:1//Расстояние от источника

A0=12.21//Амплитуда вблизи источника

a=3.3//Коэффицентпоглощения

A=A0*exp(-a*x);

xgrid()

xtitle("Затуханиеколебания","t,сек","A,мВ")

xlabel('t,c');

ylabel('A,мВ')

plot(x,A,2);

x=[0.5];

plot(x,A=A0*exp(-a*x),'k.');

xgrid()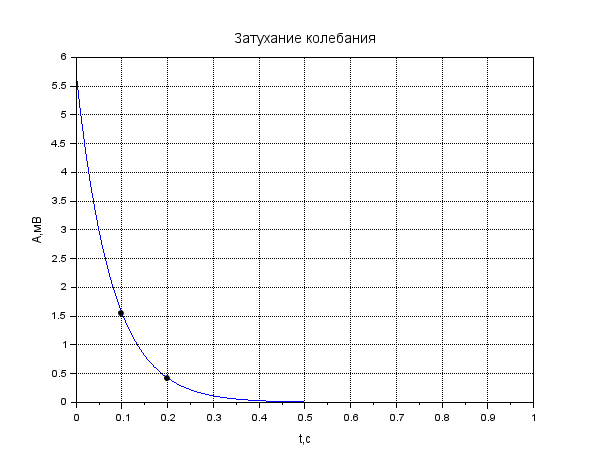



Рисунок 8. Затухание колебания в костях черепа.

Листинг:

x=0:0.01:1//Расстояние от источника

A0=5.7//Амплитуда вблизи источника

a=13//Коэффицентпоглощения

A=A0*exp(-a*x);

xgrid()

xtitle("Затуханиеколебания","t,сек","A,мВ")

xlabel('t,c');

ylabel('A,мВ')

plot(x,A,2);

x=[0.1,0.2];

plot(x,A=A0*exp(-a*x),'k.');

xgrid()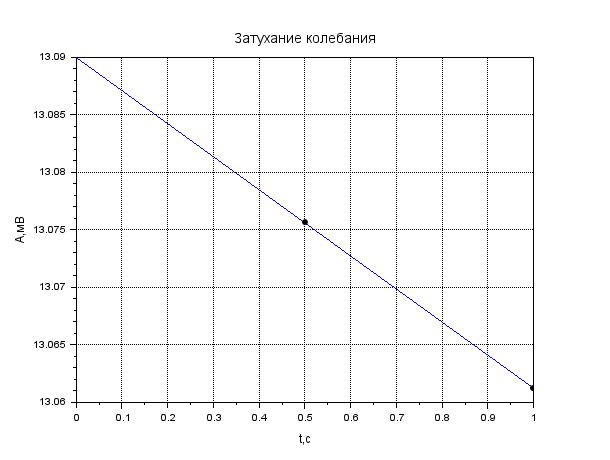



Рисунок 9. Затухание колебания в воде.

x=0:0.01:1//Расстояние от источника

A0=13.09//Амплитуда вблизи источника

a=0.0022//Коэффицентпоглощения

A=A0*exp(-a*x);

xgrid()

xtitle("Затуханиеколебания","t,сек","A,мВ")

xlabel('t,c');

ylabel('A,мВ')

plot(x,A,2);

x=[0.5,1];

plot(x,A=A0*exp(-a*x),'k.');

xgrid()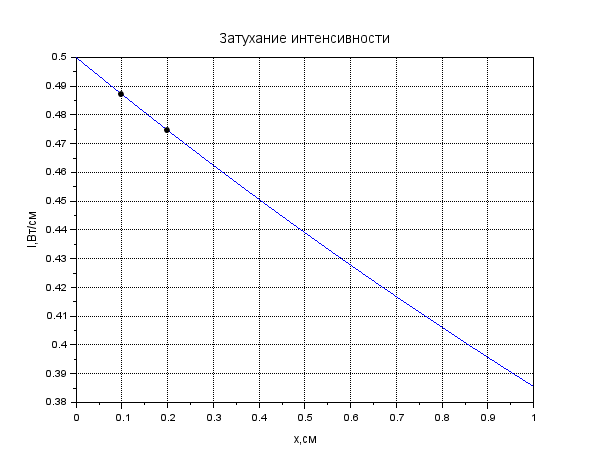



Рисунок 10. Затухание интенсивности в крови.

Листинг:

x=0:0.01:1//Расстояние от источника

I0=0.5//Интенсивность вблизи источника

a=0.13//Коэффицентпоглощения

I=I0*exp(-2*a*x);

xgrid()

xtitle("Затухание интенсивности","x,см","I,Вт/см")

xlabel('x,cм');

ylabel('I,Вт/см')

plot(x,I,2);

x=[0.1,0.2];

plot(x,I=I0*exp(-2*a*x),'k.');

xgrid()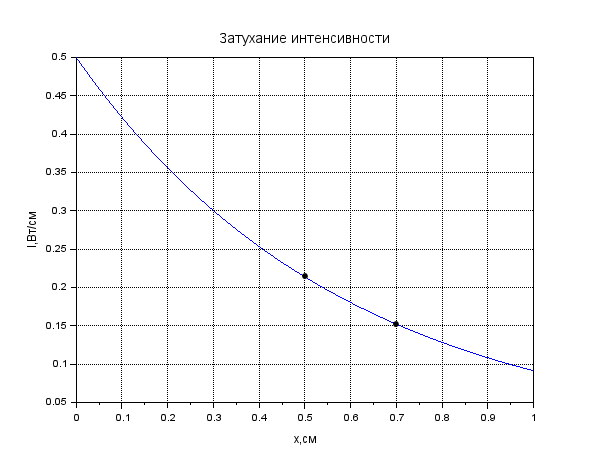



Рисунок 11. Затухание интенсивности в мозге.

Листинг:

x=0:0.01:1//Расстояние от источника

I0=0.5//Интенсивность вблизи источника

a=0.85//Коэффицентпоглощения

I=I0*exp(-2*a*x);

xgrid()

xtitle("Затухание интенсивности","x,см","I,Вт/см")

xlabel('x,cм');

ylabel('I,Вт/см')

plot(x,I,2);

x=[0.5,0.7];

plot(x,I=I0*exp(-2*a*x),'k.');

xgrid()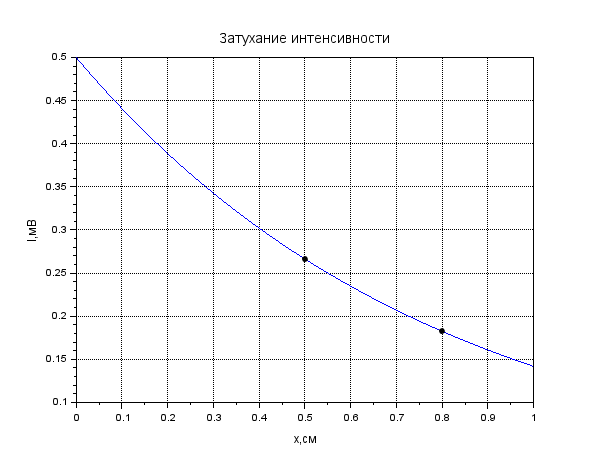



Рисунок 12. Затухание интенсивности в мозге.

x=0:0.01:1//Расстояние от источника

I0=0.5//Интенсивность вблизи источника

a=0.63//Коэффицентпоглощения

I=I0*exp(-2*a*x);

xgrid()

xtitle("Затухание интенсивности","x,см","I,Вт/см")

xlabel('x,см');

ylabel('I,мВ')

plot(x,I,2);

x=[0.5,0.8];

plot(x,I=I0*exp(-2*a*x),'k.');

xgrid()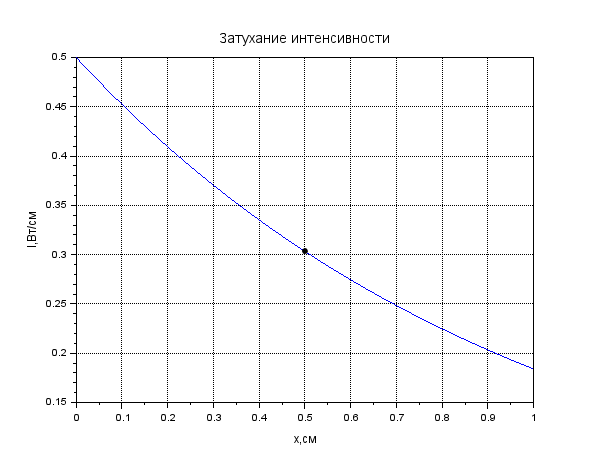



Рисунок 13. Затухание интенсивности в почке.

Листинг:

x=0:0.01:1//Расстояние от источника

I0=0.5//Интенсивность вблизи источника

a=0.5//Коэффицентпоглощения

I=I0*exp(-2*a*x);

xgrid()

xtitle("Затухание интенсивности","x,см","I,Вт/см")

xlabel('x,см');

ylabel('I,Вт/см')

plot(x,I,2);

x=[0.5];

plot(x,I=I0*exp(-2*a*x),'k.');

xgrid()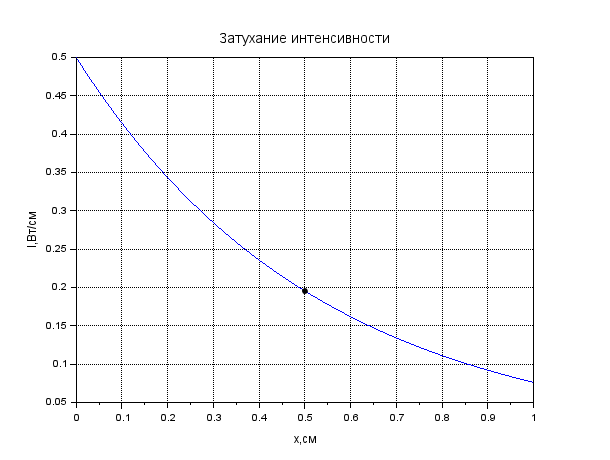



Рисунок 14. Затухание интенсивности в печени.

Листинг:

x=0:0.01:1//Расстояние от источника

I0=0.5//Интенсивность вблизи источника

a=0.94//Коэффицентпоглощения

I=I0*exp(-2*a*x);

xgrid()

xtitle("Затухание интенсивности","x,см","I,Вт/см")

xlabel('x,см');

ylabel('I,Вт/см')

plot(x,I,2);

x=[0.5];

plot(x,I=I0*exp(-2*a*x),'k.');

xgrid()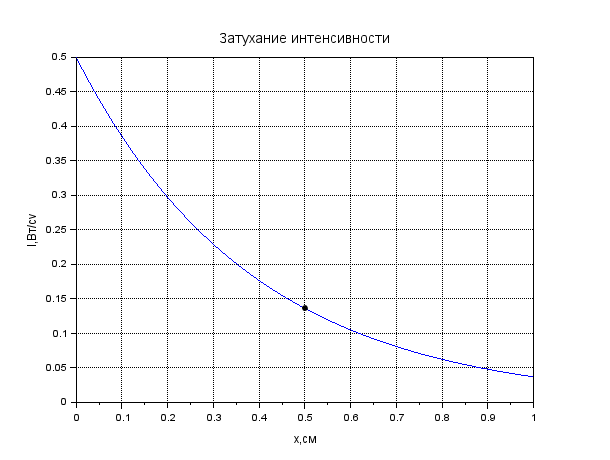



Рисунок 15. Затухание интенсивности в мышце вдоль фибрилл.

Листинг:

x=0:0.01:1//Расстояние от источника

I0=0.5//Интенсивность вблизи источника

a=1.3//Коэффицентпоглощения

I=I0*exp(-2*a*x);

xgrid()

xtitle("Затухание интенсивности","x,см","I,Вт/см")

xlabel('x,см');

ylabel('I,Вт/cv')

plot(x,I,2);

x=[0.5];

plot(x,I=I0*exp(-2*a*x),'k.');

xgrid()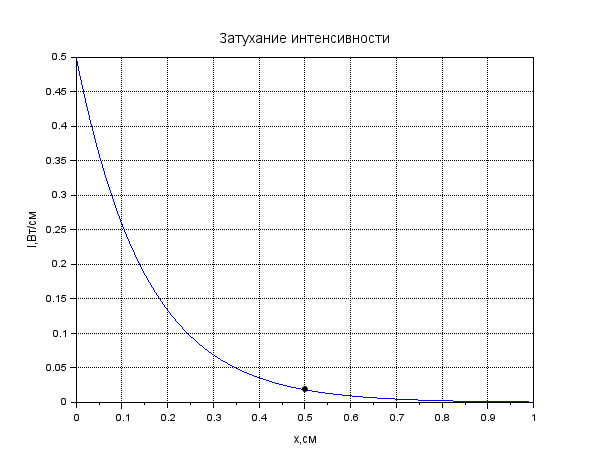



Рисунок 16. Затухание интенсивности в поперечной фибрилле.

Листинг:

x=0:0.01:1//Расстояние от источника

I0=0.5//Интенсивность вблизи источника

a=3.3//Коэффицентпоглощения

I=I0*exp(-2*a*x);

xgrid()

xtitle("Затухание интенсивности","x,см","I,Вт/см")

xlabel('x,см');

ylabel('I,Вт/см')

plot(x,I,2);

x=[0.5];

plot(x,I=I0*exp(-2*a*x),'k.');

xgrid()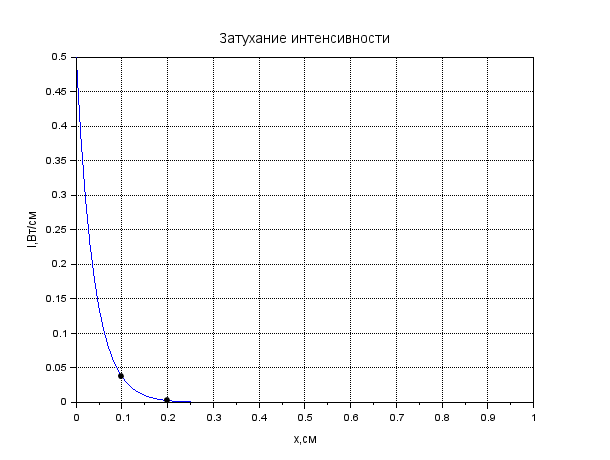



Рисунок 17. Затухание колебания в костях черепа.

Листинг:

x=0:0.01:1//Расстояние от источника

I0=0.5//Интенсивность вблизи источника

a=13//Коэффицентпоглощения

I=I0*exp(-2*a*x);

xgrid()

xtitle("Затухание интенсивности","x,см","I,Вт/см")

xlabel('x,см');

ylabel('I,Вт/см')

plot(x,I,2);

x=[0.1,0.2];

plot(x,I=I0*exp(-2*a*x),'k.');

xgrid()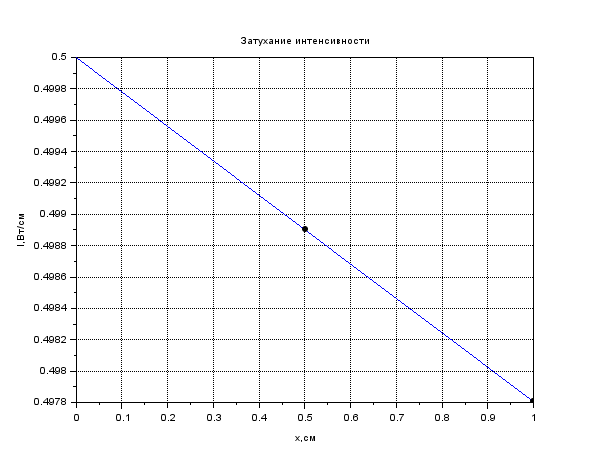


Рисунок 18. Затухание колебания в воде.

Листинг:

x=0:0.001:1//Расстояние от источника

I0=0.5//Интенсивность вблизи источника

a=0.0022//Коэффицентпоглощения

I=I0*exp(-2*a*x);

xgrid()

xtitle("Затухание интенсивности","x,см","I,Вт/см")

xlabel('x,см');

ylabel('I,Вт/см')

plot(x,I,2);

x=[0.5,1];

plot(x,I=I0*exp(-2*a*x),'k.');

xgrid()

Вывод:

Провели расчеты и представили графики моделирования амплитуды колебания частиц от расстояния х, интенсивности ультразвука от расстояния х для различных тканей.

На основе построенных графиков и полученных значений можно сказать, что затухание колебаний при прохождении ультразвука через разные среды обратно пропорционально плотности среды, через которую

проходит ультразвук. Чем меньше плотность ткани, тем медленнее затухают колебания в среде.

Рассчитать какую деформацию испытывает эритроцит при данных условиях.

Размер эритроцита = 5*10-3 см = 5*10-5м

Частота ультразвука = 1 МГц = 106 Гц

Интенсивность ультразвука = 1 Вт/см2

Амплитуда смещения в биологических средах А ≈ 2*10-6 см ≈ 2*10-8 м

Деформация эритроцита ≈ 5*10-7 см≈ 5*10-9 м

Общий вывод:

В ходе данной лабораторной работы я научилась:

· регистрировать простейшие колебательные процессы

· определять основные параметры колебаний

· представлять колебания в виде графиков в программе Scilab

Контрольные вопросы

1. 
   Какие процессы называются колебаниями?
   

Колебаниями или колебательным движением называются процессы , повторяющиеся во времени.

2. 
   Как классифицируются механические колебания?
   

По виду воздействия на колеблющуюся систему различают свободные (собственные) колебания, вынужденные, автоколебания и параметрические колебания.

- свободными (собственными) называются такие колебания, которые происходят в системе, предоставленной самой себе, после того как она была выведена из положения равновесия, т.е. осциллятор совершает колебательные движения только под действием внутренних сил.

- вынужденными называются колебания, когда колеблющаяся система подвержена воздействию внешних периодических сил.

- автоколебания – сопровождаются воздействием внешних сил, управляемых самой колеблющейся системой.

- параметрические колебания – сопровождаются периодическим изменением какого-либо параметра системы под действием внешнего воздействия

3. 
   Какие колебания называются гармоническими?
   

Гармоническими колебаниями физической величины называются такие колебания, при которых смещение тела изменяется по гармоническому (синусоидальному (sin) или косинусоидальному(cos)) закону с течением времени.

4. 
   Какие колебания называются затухающими?
   

Затухающими называются такие колебания , которые характеризуются наличием трения.

5. 
   Какими основными параметрами характеризуется колебания и в чем заключается их физический смысл?
   

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАНИЙ.

1) Амплитуда колебаний (x)— это максимальное расстояние, на которое удаляется колеблющееся тело от своего положения равновесия. Амплитуда свободных колебаний определяется начальными условиями. Единица измерения-метр (м).

2) Период колебания (Т)— это минимальный промежуток времени, по истечении которого система возвращается в прежнее состояние. Единица измерения-секунда(с).

3) Частота колебаний (V) — это число колебаний, совершаемых за 1 с. Единица измерения -герцы (Гц);

4) Циклическая частота (w)— это величина, в 2 раз большая частоты. Физический смысл циклической частоты заключается в том, что она показывает, какое число колебаний совершается за 2 секунд. Единица измерения-единица деленная на секунду (рад/с).

6. 
   Как записывается дифференциальное уравнение затухающих колебаний и его решение?
   

Затухающие колебания обозначаются уравнением: 𝑥(𝑡) = 𝐴𝑒 −𝛽𝑡cos(𝜔𝑡 + 𝜑0), где 𝛽 = 𝑟: 2𝑚 - показатель затухания, показывающий, какая доля энергии теряется при каждом колебании ( r - постоянная, называемая коэффициентом сопротивления среды, m - масса тела). Колебательный режим (β < ω0). Общее решение будет действительно и может быть записано в виде:

𝑥(𝑡) = 𝐴𝑒 −𝛽𝑡cos(𝜔𝑡 + 𝜑0), где 𝜔 = √𝜔0 2 − 𝛽2, то есть представляет собой затухающие колебания, частота которых ω меньше, чем у собственных незатухающих колебаний.

7. 
   Чему равна кинетическая, потенциальная и полная энергия гармонического колебания?
   

Полная механическая энергия колеблющегося тела равна сумме его кинетической и потенциальной энергий и при отсутствии трения остается постоянной:

8. 
   Какие эффекты возникаю при воздействии ультразвуковых волн на биологические объекты?
   

Ультразвуковые колебания, воздействуя на организм,
производят механический, тепловой, физико-химический
и рефлекторный эффекты.

Наиболее изучено биологическое действие ультразвука при контактном его воздействии. В эксперименте установлено, что ультразвуковые колебания, глубоко проникая в организм, могут вызвать серьезные локальные нарушения в тканях: воспалительную реакцию, геморрагии, а при высокой интенсивности – некроз.